輕型免維護雙腹板滑輪的極限承載能力研究

張　氫　童麗君　聶飛龍　孫遠韜　秦仙蓉

同濟大學機械與能源工程學院

?

輕型免維護雙腹板滑輪的極限承載能力研究

張氫童麗君聶飛龍孫遠韜秦仙蓉

同濟大學機械與能源工程學院

對新研制的某直徑1 800 mm輕量化高速重載薄壁雙腹板滑輪的抗壓失穩能力進行了分析。先對滑輪采用殼單元建模型進行線性屈曲分析，得到了其特征值臨界載荷和第一階屈曲模態，并以其作為加載和變形依據對滑輪進行非線性屈曲分析，求得其臨界失穩載荷值為423 t，滑輪的加載載荷-側向位移曲線與彈塑性屈曲理論一致。為驗證滑輪的有限元仿真的正確性，設計了1臺滑輪動載模擬試驗臺，在2種工況下對滑輪進行試驗，發現試驗結果與計算結果非常接近。

滑輪; 動載試驗; 塑性屈曲; 弧長法

1　引言

傳統的大型滑輪通常采用單腹板式結構，根據起重機設計規范確定的腹板厚度在實踐中被證明是偏于保守的，按這種方法設計的滑輪不僅浪費鋼材，而且質量偏重，很難滿足如今港口起重機輕量化的要求。同時，由于其質量偏重引起的轉動慣量偏大，對起重機起升機構高速運行帶來不利。為此，研發了一種新型輕型冷軋薄板滑輪。該輕型滑輪由2塊用通孔穿管焊接在一起的腹板組成，所焊接的每塊腹板上均布有8個穿孔，繩槽底徑為1 800 mm。該滑輪采用雙腹板箱型結構，質量輕，剛度大且強度高[1]。為了解其薄壁腹板結構在大過載時的抗失穩能力，本文采用弧長法求解了該滑輪的失穩載荷，并用實驗驗證了滑輪模型的正確性。

2　滑輪的建模和載荷分析

2.1滑輪的建模

由于滑輪的雙腹板的厚度遠小于腹板其他兩維的尺寸，屬于薄壁結構，選用殼單元來模擬，全部采用殼單元按照其實際尺寸建模。根據圖1(a)中的設計模型，可以在ANSYS里使用shell181單元建立如圖1(b)所示的滑輪模型，共有30 871個網格和26 412個節點。

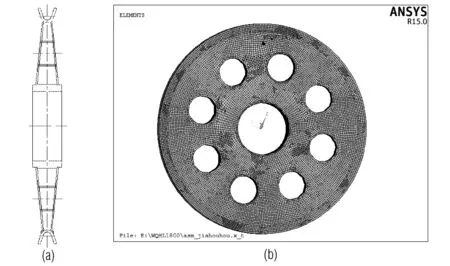
圖1　滑輪的設計模型和有限元模型

2.2滑輪的載荷分析

取滑輪的一段微元進行受力分析見圖2。假設不考慮繩槽和鋼絲繩的摩擦，在鋼絲繩上的拉力為一定值T，則繩子微元對繩槽徑向壓力為：

(1)

由于θ很小，可以使用

(2)

對其進行化簡，可得:

(3)

式中，σN為線載荷，N/m 。由力的分解原則，可得:

(4)

同理可得:

(5)

綜合式(4)、(5)可得

(6)

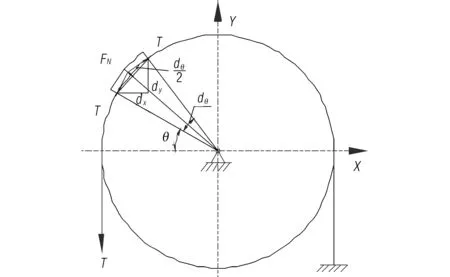
圖2　滑輪微元受力示意圖

鋼絲繩型號為D-6×37+FC-54-182，所適用抓斗卸船機額定起重量62 t，實際工作中鋼絲繩載荷為62×0.66÷2=20.46=210 kN，滑輪承受載荷為420 kN，其中0.66為抓斗偏載系數，2為單組鋼絲繩根數，此時鋼絲繩取9倍安全系數。滑輪兩側鋼絲繩對繩槽產生擠壓作用，滑輪半徑R為900 mm，滑輪繩槽寬度為74 mm，假設繩槽所受壓力近似按均布力計算，則壓力為:

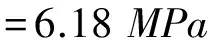
(7)

滑輪與滑輪軸之間存在相對轉動，二者之間通過軸承連接，輪轂與軸承外圈之間為過盈配合，滑輪軸與軸承內圈之間為間隙配合，滑輪承載的時候只有滑輪輪轂與軸承上半部分的約束起作用，因此只用約束滑輪輪轂上半部分節點的自由度。按照上述計算的結果施加載荷，即將鋼絲繩對繩槽的壓力p施加于滑輪上半部分的繩槽表面。

3　滑輪的屈曲分析

3.1特征值屈曲分析

該滑輪的雙腹板箱型結構在受壓時，當壓力達到一定值時可能會沿滑輪的側向失穩，因此需要對滑輪進行屈曲分析，求解其屈曲失穩的臨界載荷。

在運用特征值方法進行屈曲分析時，需要注意滑輪的自重是恒載，而恒載應力剛度不應被屈曲載荷系數縮放。這樣需要不斷改變所施加的載荷中活載的大小，經過多次有限元求解，然后對每次計算中求得的特征值和對應的活載進行插值計算[2]，以得到特征值為1時外載荷的大小,分析流程見圖3。

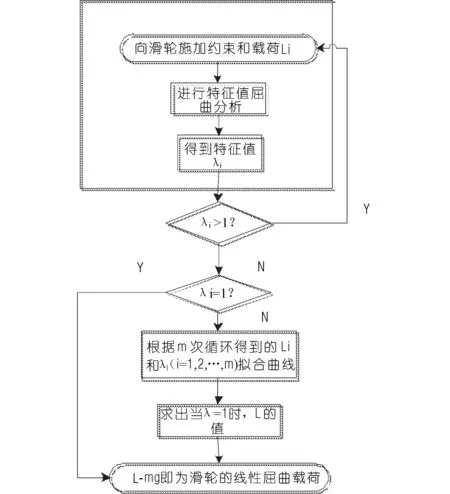
圖3　特征值屈曲分析流程圖

這樣求得屈曲特征值為1時，施加的總載荷為20 678 kN，減去滑輪的自重，滑輪的線性臨界屈曲載荷為20 673 kN。在滑輪上加載該臨界載荷值，滑輪最大von Mises應力已經達到了2 000 MPa左右，顯然滑輪材料早已進入了塑性變形階段，與實際不符。特征值屈曲分析方法要求材料必須在線彈性范圍內受載，而滑輪在屈曲之前早已進入了塑性變形階段，從而導致過高的估計了滑輪的臨界屈曲載荷。要想準確地分析滑輪的臨界屈曲載荷，需要定義滑輪材料Q345B在屈服點以后的應力應變數據[3]。使用ANSYS里的多線性隨動強化材料模型來定義材料的應力應變數據，見圖4。

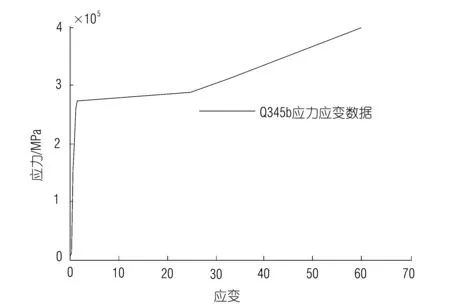
圖4　滑輪材料的應力應變數據

3.2滑輪的非線性屈曲分析

利用滑輪的第一階模態振型來施加非線性屈曲分析中的初始缺陷。由圖5可知，需沿側向對滑輪施加微擾力，微擾力可取為當鋼絲繩相對于滑輪偏載3°時的側向力，為135 kN均布于滑輪繩槽上半部的壓力。當所施加的載荷類型為力時，在滑輪變形過程中，每一個子步中力都會一直保持最初的方向，這明顯與滑輪的真實受力情況不符。如果所施加的載荷類型為壓力，壓力會跟隨滑輪結構的變形過程而改變方向，因此滑輪上的載荷和微擾力都選為均布壓力。

圖5　滑輪一階特征值對應的屈曲模態

非線性屈曲分析能夠考慮材料的塑性變形對臨界屈曲載荷的影響，其基本步驟為：逐步地增加載荷增量和微擾力，當所加的載荷增量與滑輪最大側向位移增量的曲線斜率減小時，減小步長，以獲得精確的臨界載荷。本次非線性屈曲分析一共被分成了21個子步，通過提取21個子步中的垂向載荷值和側向最大位移值，并對其進行曲線擬合，可求得滑輪的加載載荷與其對應的最大側向的位移的曲線，如圖6所示，在加載載荷為4 230 kN，最大側向位移為48 mm時滑輪出現極值點屈曲。當載荷超過4 230 kN時，滑輪的側向位移在加載載荷減小時仍在增加，可知423 t為滑輪的壓潰載荷。

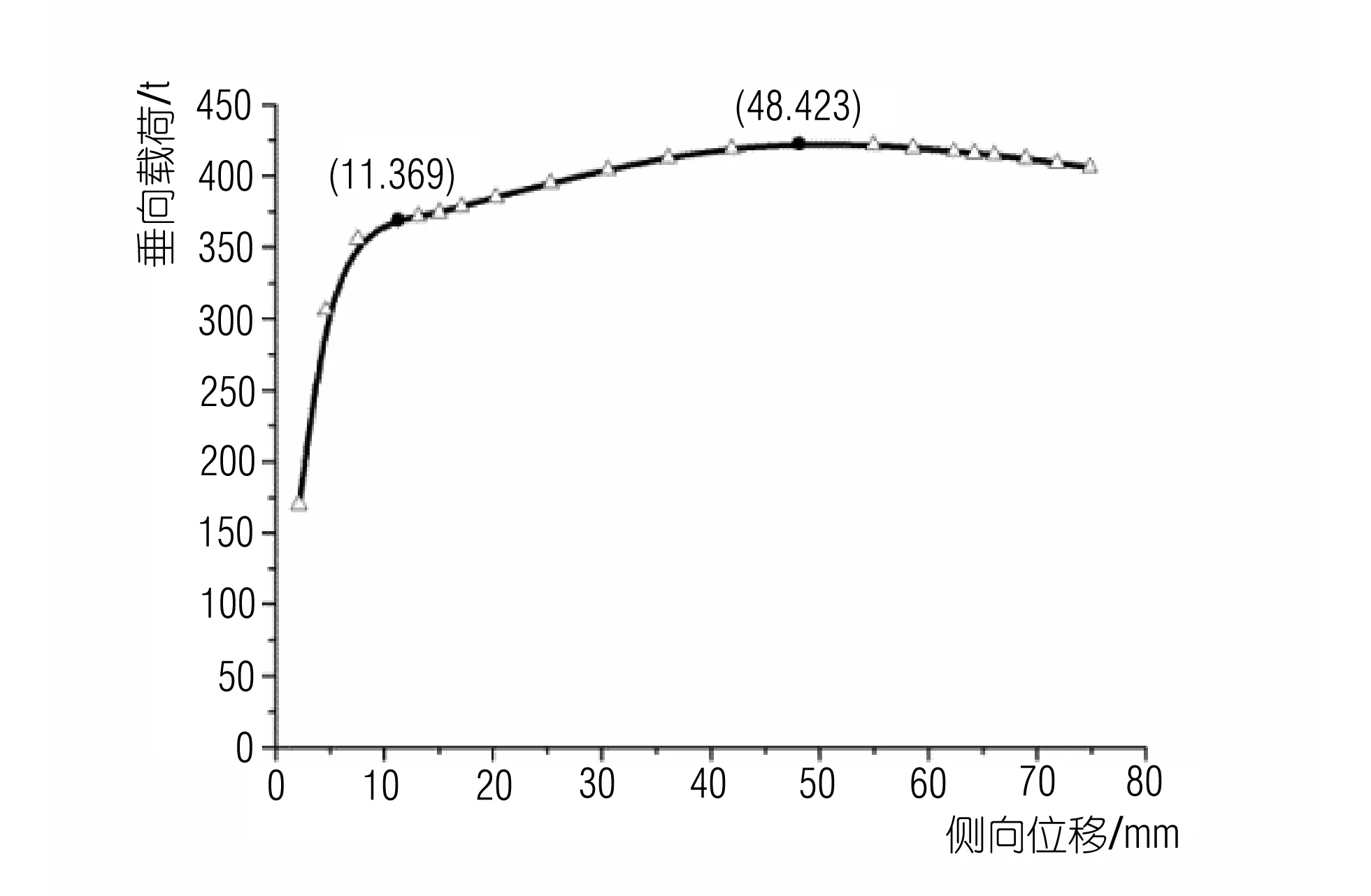
圖6　非線性屈曲分析中滑輪的橫向位移和載荷的曲線

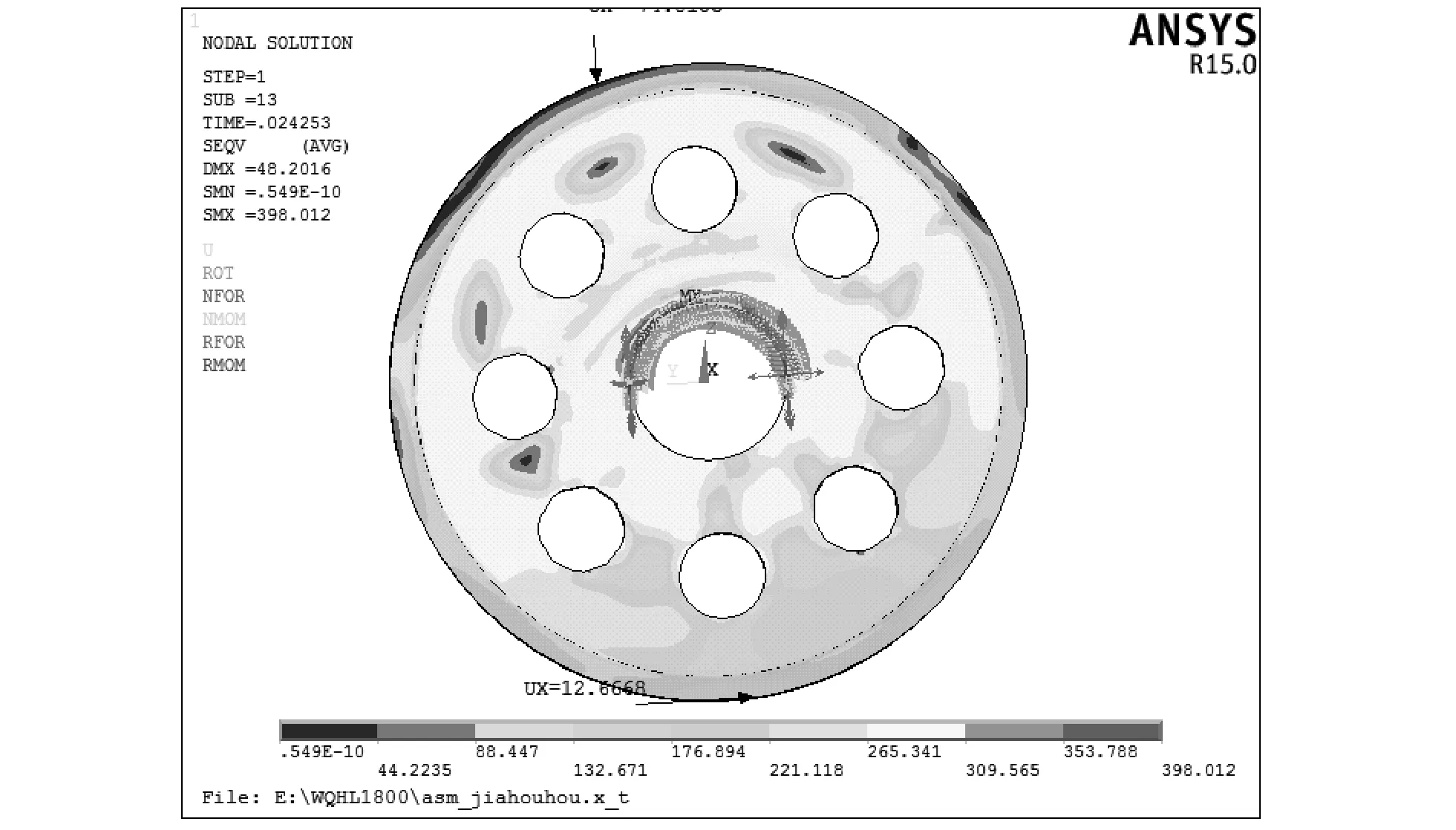
圖7　滑輪屈曲時的von Mises應力分布云圖

3.3滑輪屈曲分析的理論驗證

非線性屈曲分析中，每一個子步都會增加相應的載荷，在逐步加載的過程中，滑輪的應力在經過屈服點后，如圖4所示，會到達屈服階段；此時滑輪載荷不需要增加，滑輪材料的應變也會顯著增加，最終體現為滑輪的側向位移的增加，如圖6中的點(11.369)及其以后的曲線所示。當滑輪材料經過屈服階段后，到達強化階段時，需要增加載荷來使之進一步變形；當材料應力超過抗拉極限后，滑輪無法進一步承受更高的載荷，此時即使載荷有所減少，滑輪的側向位移依然會繼續增大，最終滑輪被壓潰失穩，如圖6中的點(48.423)及其以后的曲線所示。該點也對應著塑性屈曲分析中的極值點失穩這一情況，此時滑輪所承受的載荷被稱為壓潰載荷[4]，為4 230 kN。

4　滑輪的試驗與驗證

4.1滑輪的靜強度分析結果

圖8為滑輪處于正常工況420 kN的載荷下時的von Mises應力云圖。滑輪較大的應力分布于輪轂受約束處和滑輪上半部分的3個通孔處，最大von Mises應力為73.7 MPa，位于輪轂處。

圖9為繩槽在正常工況下的von Mises應力分布云圖。在施加壓力的部分繩槽受力比較均勻。繩槽上最大應力為39.5 MPa，施加壓力的部分繩槽壓力范圍為26.3 MPa到39.5 MPa，其余未施加壓力的部分基本上不受壓力。

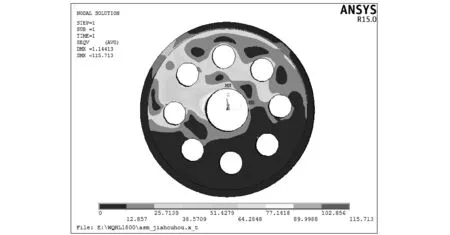
圖8　正常工況下滑輪von Mises應力分布云圖

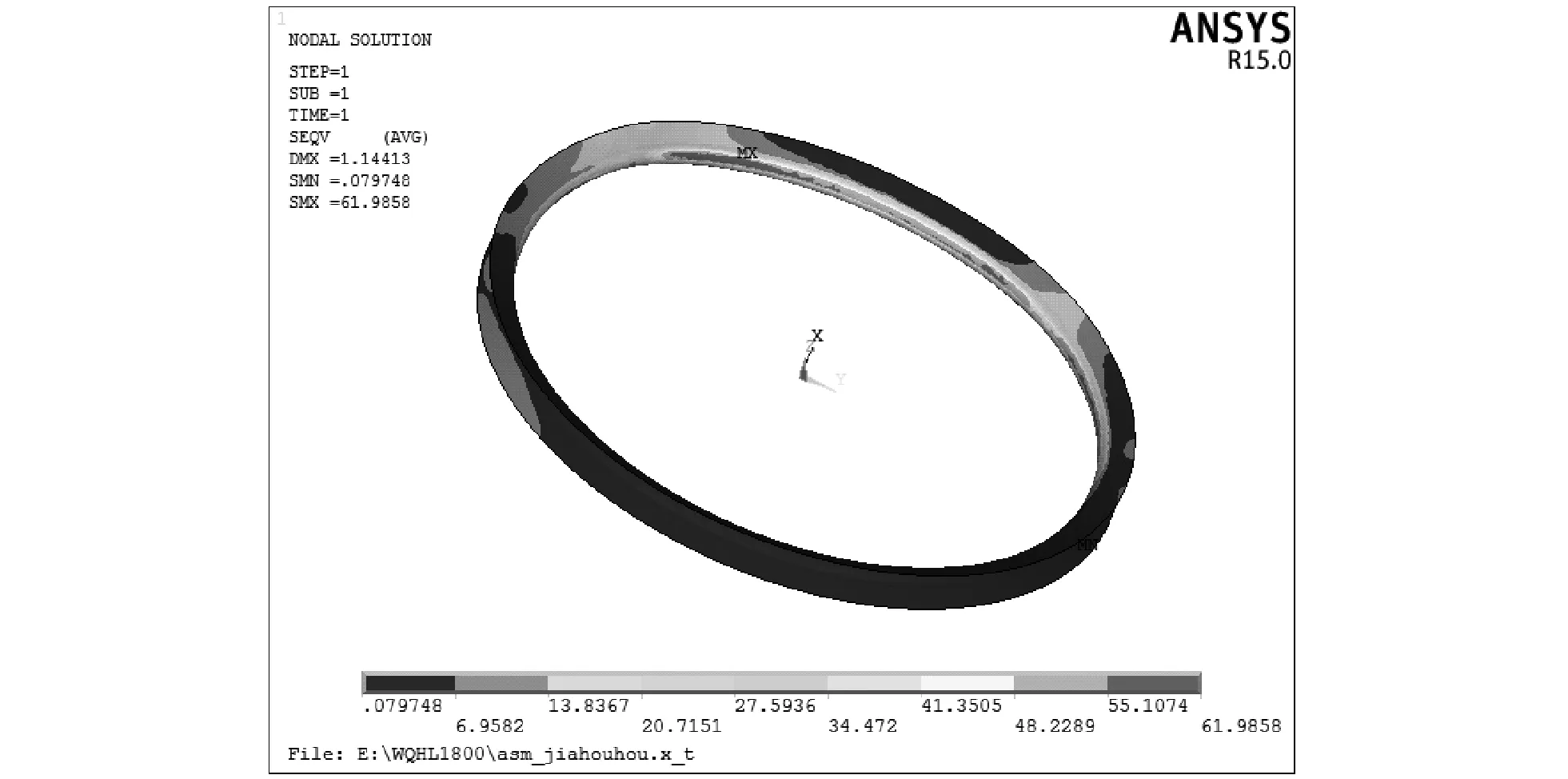
圖9　正常工況下繩槽von Mises應力分布云圖

4.2滑輪的試驗結果及其與計算結果的比較

由于軸承承載能力限制，所以不能做滑輪極限承載能力實驗。為了驗證上述非線性屈曲計算中有限元模型的正確性，設計了2組實驗。工況1是不計微擾力時，使滑輪具有2倍安全系數，加載840 kN的試驗；由于計算得到的滑輪的壓潰載荷為4 230 kN，考慮到計算的誤差，需要準備更大的載荷對滑輪進行試驗，該實驗條件難以達到；同時，即使載荷條件能夠達到，該滑輪所使用的軸承承載能力有限，實驗難以進行；因此擬用鋼絲繩相對滑輪具有3°的偏角、滑輪受載840 kN的工況2來代替，并求解相同條件下的滑輪模型的應力分布與試驗對比。

滑輪在工況1中試驗測得的結果見圖10。

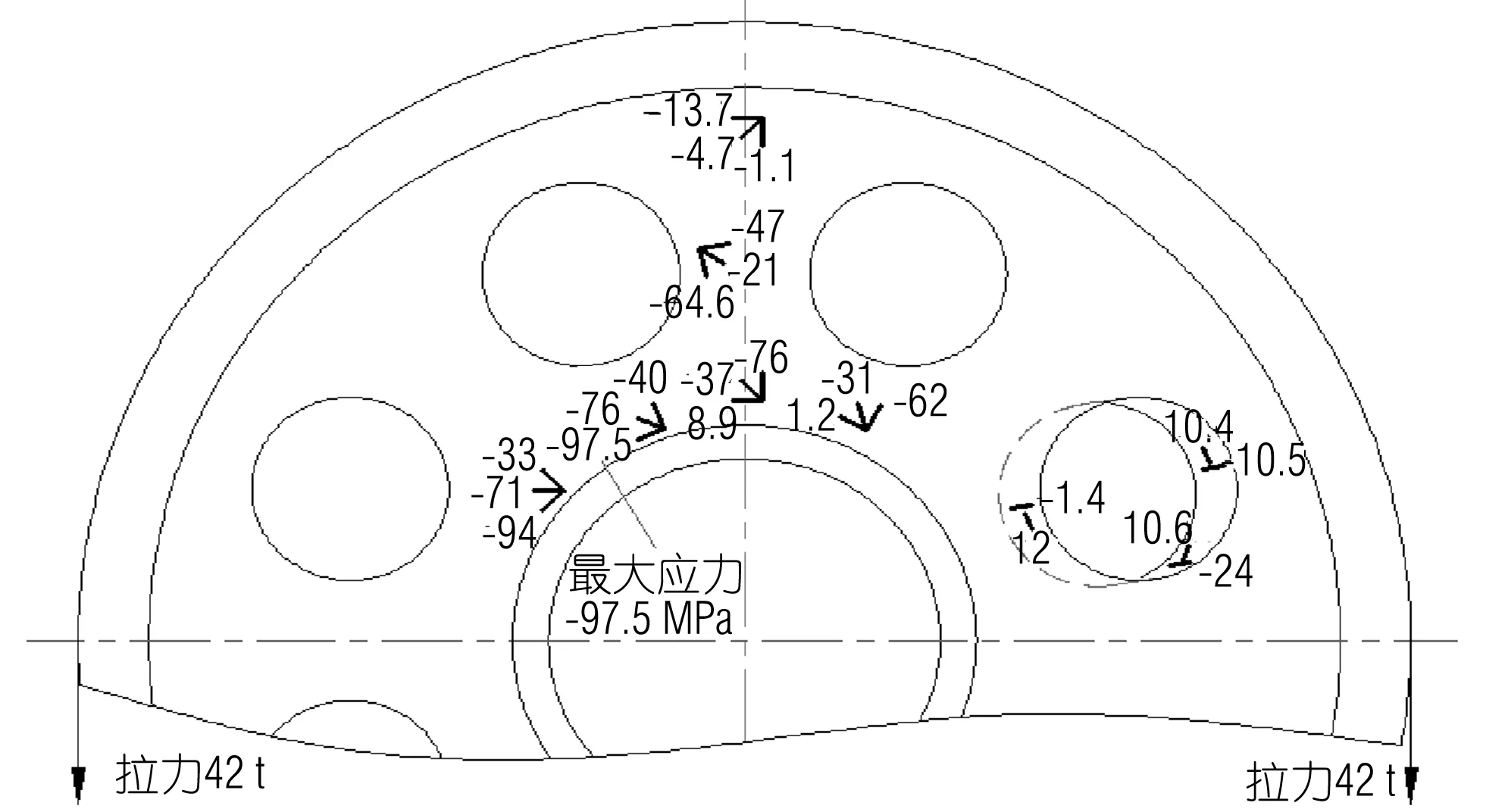
圖10　工況1下滑輪實驗測點的應力值(MPa)

根據材料力學的相關知識，可以根據測點的三向應力值求出每個測點的von Mises應力值。將每個測點的von Mises與有限元計算結果進行對比，有限元中測點的結果見圖11，每個測點的試驗結果與有限元計算結果非常接近，正如表1所示，二者之間最大誤差不超過13.6%。

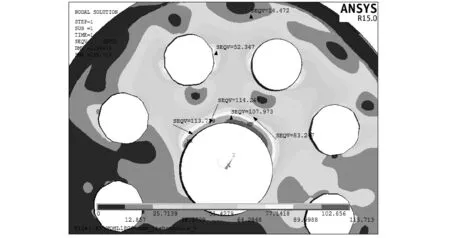
圖11 　工況2下滑輪在有限元計算中的測點結果(MPa)

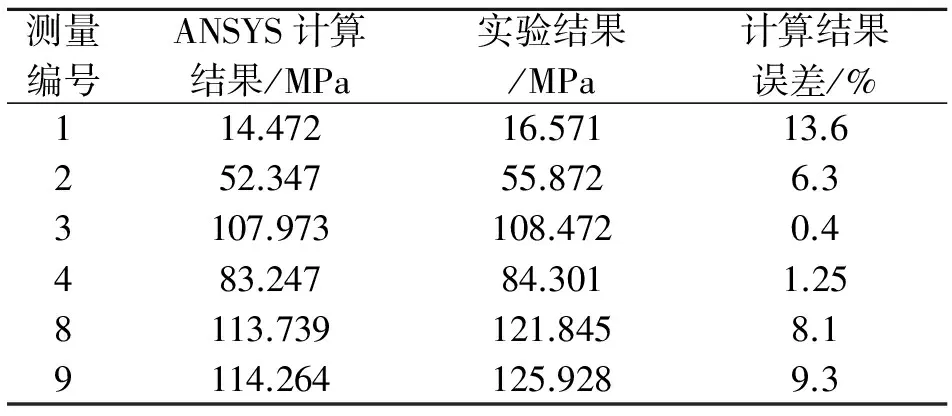
測量編號ANSYS計算結果/MPa實驗結果/MPa計算結果誤差/%114．47216．57113．6252．34755．8726．33107．973108．4720．4483．24784．3011．258113．739121．8458．19114．264125．9289．3

按照上面所述的方法，同樣可求出滑輪在工況2下的各個測點的von Mises應力。表2對比了相同載荷條件下的ANSYS的計算結果和試驗結果，二者之間的誤差最大只有6.8%，說明了滑輪的有限元模型的準確性及其計算結果的可信度。

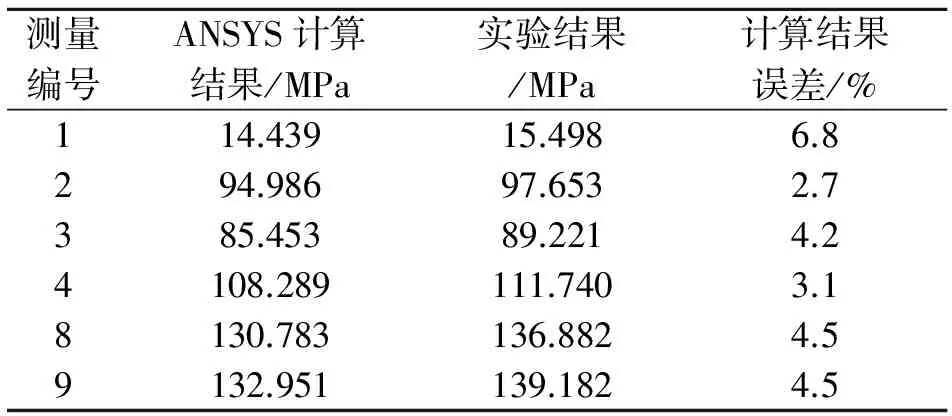
表2　某型塔機基礎節及加強節之間各向連接剛度初始值

5　結語

本文用殼模型研究了雙腹板滑輪的屈曲模式，首先用特征值屈曲分析求得其線性臨界載荷值和第一階模態振型，發現在載荷達到線性臨界載荷值之前滑輪材料Q345b已經進入塑性變形階段，滑輪的屈曲模式為塑性屈曲。考慮材料的塑性變形，使用弧長法對滑輪進行非線性屈曲分析，得出了滑輪的壓潰載荷。

研究發現：運用特征值屈曲分析方法得到的滑輪的壓潰載荷，約為非線性屈曲分析得出的壓潰載荷的5倍，其結果對于滑輪的塑性屈曲分析的參考價值很低，這是由于特征值分析的原理所決定的；材料的塑性對臨界載荷有明顯的降低，滑輪的失穩形式為極值點失穩，當滑輪所承受的載荷超過壓潰載荷4 230 kN后，滑輪的側向位移將會迅速增大，滑輪也因此失去了承載能力。

[1]張氫,鄭安康,蘇先裕等. 一種免維護的滑輪裝置[P]. 上海：CN104776195A,2015-07-15.

[2]秦仙蓉,孚羅特,劉應花等. 基于有限元方法的塔機桁架結構屈曲分析[J]. 中國工程機械學報,2013,03:187-189+204.

[3]李兆凡,石永久,陳宏等. 改進型鋼結構梁柱節點非線性有限元分析[J]. 建筑結構,2002,09:15-18.

[4]翁智遠. 圓柱薄殼容器的振動與屈曲(精)[M]. 上海：上海科技出版社, 2007.

張氫：201800，上海市嘉定區曹安公路4800號上海市嘉定區同濟大學嘉定校區

Study of the Ultimate Loading Capacity of the Pulley with Two Webs

Zhang QingTong LijunNie FeilongSun YuantaoQin Xianrong

School of Mechanical Engineering, Tongji University

Through the analysis of instabilityin compression for the new kind of pulley(whose diameter is 1800 mm)that presents advantages of light weight, high speed, heavy load and double thin-walled webs,the authors obtained both the linear critical load and the first buckling mode by conducting an eigen-buckling analysis of the pulley. After the nonlinear buckling analysis has been conducted according to the first buckling mode, the critical buckling load of the pulley is calculated to be 423 ton, which is 5 times of the normal load that the pulley bears. The curve of the vertical load and the lateral displacement for the pulley is consistent with the plastic buckling theory. In order to test the correctness of the FEA analysis of the pulley, a dynamic testbed for the pulley has also been designed. Experiments have been conducted on the pulley in two cases, and it is found that both the experimental and simulation results coincide with each other well.

pulley; dynamic test; plastic buckling; arc-length method

國家自然科學基金項目資助(51205292)

國家科技支撐計劃課題資助(2014BAF08B05，2015BAF06B05)

2016-06-23

10.3963/j.issn.1000-8969.2016.05.001