數學思想方法在數學解題中的應用研究

江蘇鹽城幼兒師范高等專科學校（224000） 臧亞東

數學思想方法在數學解題中的應用研究

江蘇鹽城幼兒師范高等專科學校（224000） 臧亞東

小學數學解題中涉及多種數學思想方法，重視數學思想方法的有效滲透和靈活運用，有助于深化和鞏固學生對知識的理解，提升學生的思維品質，增強學生的解題能力，培養學生良好的數學素養。對此，教師要引領學生把握轉化思想，變換形式，化繁為簡；注重整體思想，縱觀全局，化難為易；巧用分類思想，各個擊破，積零為整。

數學思想方法數學解題應用

數學思想方法是人們對數學知識的本質認識，是分析和解決數學問題的指導方法和基本策略。引導學生正確理解、掌握以及靈活運用數學思想方法，可促使學生領會數學真諦，發散數學思維，開闊解題思路，提高分析及解決問題的能力。

一、把握轉化思想，變換形式，化繁為簡

在小學數學解題中，學生有時會遇到一些關系隱晦、復雜生疏、難以解決的數學問題。此時，教師可以引導學生進行觀察、分析、聯想、類比，巧借轉化思想，將不熟悉、不規范、復雜、抽象的問題轉化為熟悉、規范、簡單、具體的問題。這樣，往往可以收到意想不到的效果。

解析：該題中A校學生總數和B校學生總數的關系比較隱蔽，此時我們可以把已知條件中“A校學生人數的等于B校學生人數的轉化成“A校學生人數與B校學生人數的比是，這樣使復雜的問題變得簡單起來。由此可以求出，A校學生人數校學生人數

【說明】在運用轉化思想解題時，需要注意轉化的等價性，注重對所給問題的隱含條件的挖掘，從而使得問題得到迅速、巧妙地解決。

二、注重整體思想，縱觀全局，化難為易

在小學數學解題中，當某些問題學生從其每個部分或條件去分析解決存在較大難度時，教師可以引導學生將數學問題中的各個部分或條件看成一個系統或整體，縱觀全局，全面分析，進而使問題得以快速、有效的解決。

【例2】小張、小李、小趙三人合修一段高速公路，小張修的路是小李和小趙兩人所修的路的，小李修的路是小張和小趙兩人所修的路的，小趙共修了1250米。這段高速公路長多少米？

【說明】在運用整體思想解題時，需注意從問題的整體性質出發，把握問題整體結構的特性，從而導出問題局部元素的特性，找到解決問題的突破口。

三、巧用分類思想，各個擊破，積零為整

在有些數學問題中，由于條件與問題之間的聯系是多向的，存在多種情況。此時為了便于有效求解，需要對各種出現的情況進行合理分類，然后逐一分析討論，各個擊破，最后綜合歸納，積零為整，得出最終的答案。

【例3】六份同樣的禮物，全部分給四個孩子，使每個孩子至少獲得一份禮物的不同分法共有多少種？

解析：由題意可知，每個孩子最少可分到一份禮物，最多不會超過三份禮物，所以此題可根據下列兩類方法來分：①一個孩子分得3份，其他孩子各分得1份，共有如表1中4種分法；②兩個孩子各分得2份，另外兩個孩子各分得1份，共有如表2中6種分法。綜合①②可知，使每個孩子至少獲得一份禮物的不同分法共有：4+ 6=10（種）。

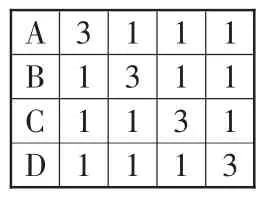
表1　

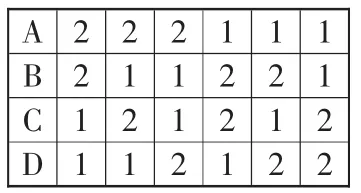
表2　

【說明】巧用分類思想解題，要注意分類的合理性，做到全面統一，不遺漏，不重復，從而提高解題的嚴密性和完整性，確保解答準確無誤。

總之，數學思想方法靈活多樣，在平時的數學教學中，教師應從教學實際出發，有效滲透數學思想方法，讓學生正確掌握和靈活運用數學思想方法，從而發展學生的數學思維，提升學生的數學解題能力。

（責編黃春香）

G623.5

A

1007-9068（2016）32-088