基于層次分析法的英那河水利工程項目成本風險管理研究

都吉慶

(大連花園口經濟區農村經濟發展局，遼寧 大連 116423)

?

基于層次分析法的英那河水利工程項目成本風險管理研究

都吉慶

(大連花園口經濟區農村經濟發展局，遼寧 大連 116423)

文章根據不同影響因子對水利工程的影響從程度，通過層次分析法進行風險因素的結構劃分，對風險影響因子通過三角模糊數方法進行模型的構建，并將模型應用到具體的工程案例中，使得水利工程的企業化管理制度水平得到提高，并取得了良好的經濟和社會效益。

層次分析法；水利工程項目成本；三角模糊數；成本風險管理

科技的發展帶動了市場競爭壓力的不斷擴大，推動著水利工程的管理制度體系在不斷地完善，逐漸形成了以項目管理為主的企業化管理體系。水利工程企業化管理制度必須以項目成本管理制度為核心，通過現代管理制度進行項目成本的安排來達到最高的經濟效益和最好的社會效益。現在企業化管理制度較粗放，項目經理能力的欠缺以及對項目成本的分配的不合理等因素，都會給水利工程造成一定的成本風險。本文通過建立數學模型來進行項目成本的風險管理制度評價。

1 模糊層次分析法

層次分析法是主要是針對一些比較復雜的體系進行層次化的細分，使得整個分析過程簡單易懂，達到了定性分析和定量分析的結合化。通過這種手段，研究人員可以對復雜問題進行細化，把復雜的影響因素進行分成許多影響因子，對各個因子之間進行簡單的計算和比較，進而可以求得不同影響因子的權重值，可以方便確定最佳的方案[1]。

2 模型的構建

水利工程成本的影響因子多而且還不確定，是相對比較復雜的工程。風險率和不確定因子是導致水利項目成本出現風險的根本元素。

2.1 建立風險因素的層次結構

風險因素的劃分通過智暴法對風險因素的種類進行判別，結合專家意見以及水利工程項目管理的制度特點，對風險因素的影響進行以下幾種形式的劃分，經濟、管理、內外部組織、技術、工程環境等風險作為第一層,并根據具體的情況進行各個因素的進一步劃分，具體的風險因素的劃分情況見表1。

表1 水利工程風險因素表

2.2 判斷矩陣的構造

AHP方式是以1～9之間的整數和各個整數的倒數為一個依據，通過這個依據來構造出判斷矩陣。有多重因素可對水利工程的項目成本產生影響，這些因素可以任意方式組合，具有很大的隨機性以及模糊性，這些相互組合的因素構成其風險因素，由于其組合的隨機性和模糊性使得單一的層次分析方式不能夠準確做出判斷。某兩種風險因素i、j對整個項目成本影響程度難以準確度量，我們能夠得到的只是兩種因素的可能最大值m和變化范圍在某個區間l、u，以上就是模糊判斷的定義。當假定給定其一個整數數值時，得到的推斷結果與預期結果不符，各個非精確結果層層疊加，產生的最終結果可能會導致風險管理體系的運行失敗。這也就是在模糊環境種我們要把層次分析方法進一步的完善和擴展。為完成擴展，將一個新的理論三角模糊數引進來，用來將兩風險因素相互比較時定量的表示結論，詳細的判定標準見表2。

表2 AHP判斷標度的設定

根據第一層的風險因素集合(A1,A2,… ,A6),我們的相應方面的資深專家對其進行分析，將各個因素一一相互對比得出結論，再通過表2種的判斷標準，得到各個資深專家的評估結論，見表3中的判斷矩陣。以表3為基礎在考慮各位專家的經驗以及研究背景，再通過分析計算不斷修正最終得出所有專家的平均綜合判別矩陣。

表3 專家判斷矩陣

2.3 一致性驗證以及層次的排序

以各位專家推薦的層次結構圖為依據，在風險識別的過程中再將模糊分析方法應用到層次分析中去，分析出各個層次里所含風險因素所占的比重，對此可以看成風險因素的先后順序的根據，逐步淘汰次要因素找到主要的風險因素，使得投標決策和項目成本預控可順利完成。

3 工程實例

3.1 工程概況

英那河共有兩條支流，一條發源于玉石之鄉的鞍山市岫巖縣，另一條發源于“北方小桂林”莊河市冰峪溝，全長95km。受2012年第10號臺風“達維”的影響，自8月3日2時起，莊河市南部地區普降大到暴雨，北部地區普降暴雨到大暴雨，局部特大暴雨，雨量時空分布不均，其中莊河最大降雨量390mm。此次強降雨造成英那河流域發生大洪水，特別是英那河上游流域降水量接近50a一遇標準，局部地區出現不同程度的洪澇災害。英那河經過2012年“8.04”大洪水沖刷后，多處形成險段，河道防洪能力低下。每遇到較大洪水，河水必淹河槽，嚴重地阻礙了當地經濟發展，另外由于河道在經過附近村屯段比降變緩，使河水中的泥沙沉積，造成河道淤塞，也影響了水流通過，為此需對莊河市境內的英那河河道進行規劃，在保證能通過設計洪水的基礎上，規劃整治河道，修建兩岸的堤防，確保洪水泄流順暢，保護兩岸人民的生命和財產安全。

3.2 風險因素層次結構的確立

依托工程實際，邀請相關專家在企業現有的生產條件下對項目工程進行評價，由表1可查得影響該項目的主要風險因素。對所有風險因素進行分析歸納，邀請3位專家對項目的第一層風險因素一一對比，依據判別標準進行打分。通過分析可分別得到3位專家建議所占比重各自為0.4，0.3，0.3。最終結論如表4所示。

根據表4的綜合評定矩陣，把所有影響因素的中間數mij抽出組成一個新矩陣:

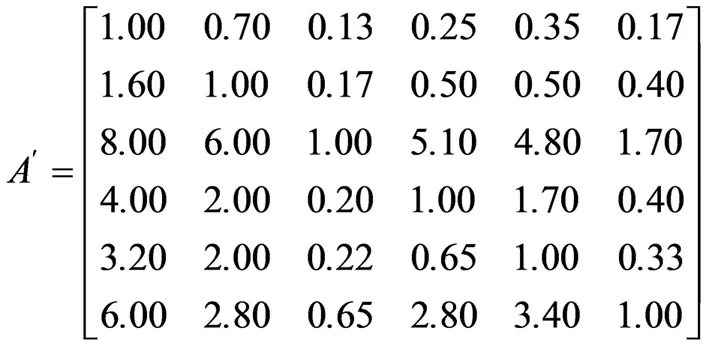
求解

(1)

式中：ω為矩陣A′的特征向量；λmax為A′的特征值。

其中：

w=(0.040,0.066,0.417,0.122,0.099,0.255)

λmax=6.272;C1=(λmax-n)(n-1)=0.054

R1=1.14;CR=C1/R1=0.048≤0.1

進而可以得出，矩陣A也能滿足一致性的要求。

把對應的數據代入到層次單排序和層次多排序公式[1]，進而可以求出第一層的風險因素的權重大小，具體的大小為見表4。

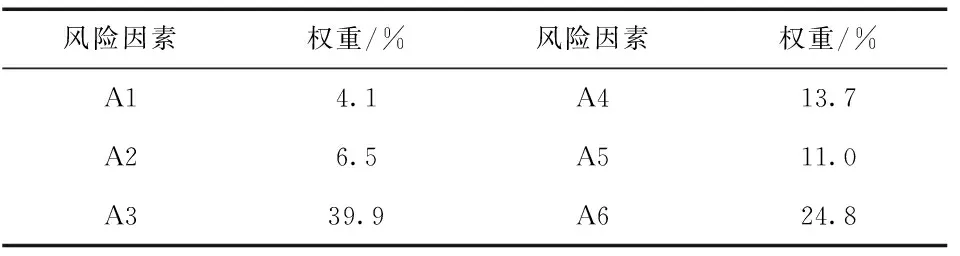
表4 第一層風險因素的權重值

通過專家評定結果，根據模糊層次分析法綜合確定第二層風險影響因子的權重值。具體如表5所示。

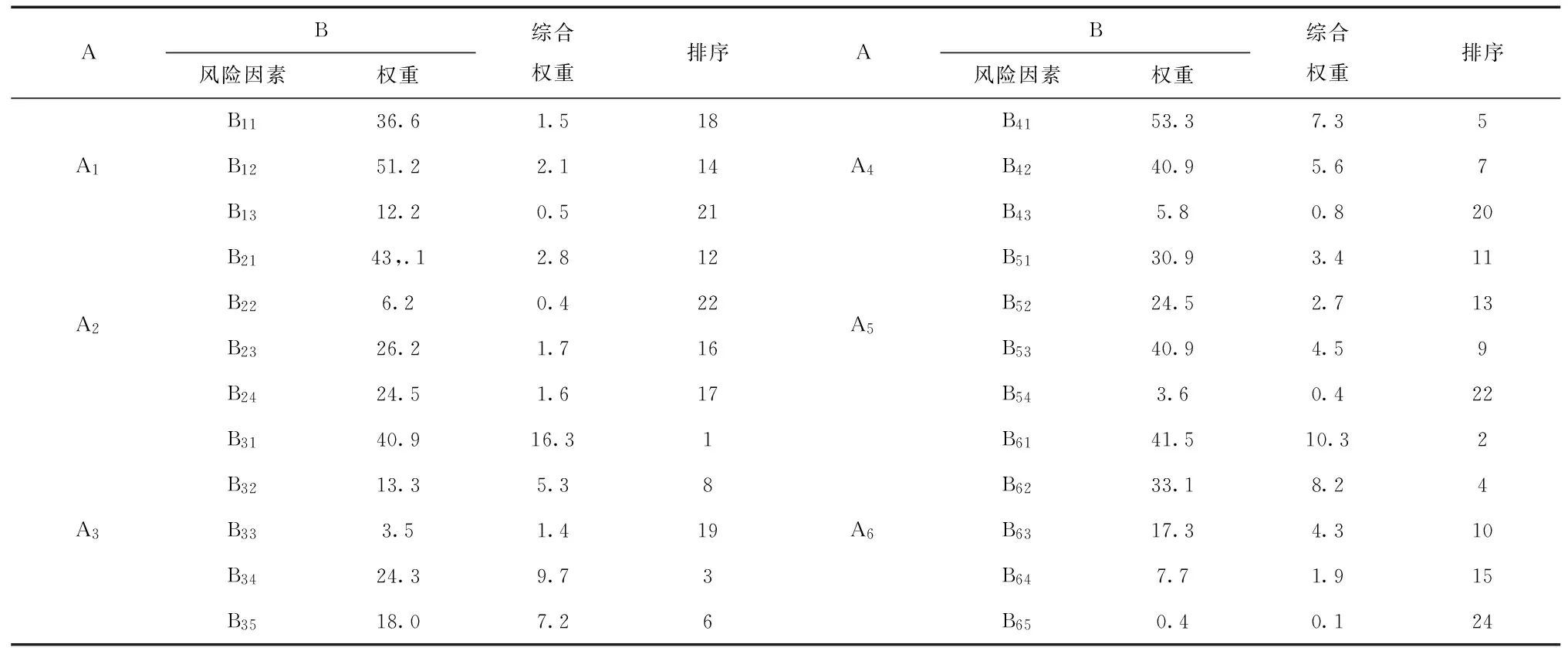
表5 第二層風險因素權重表

對上述確定的影響因子權重在前八位的影響因子作為判斷風險影響因子的主要影響因素，需要對其進行全面的控制，具體的控制措施情況如表6所示。

表6 主要風險因素來源及控制措施

所做出的風險應對措施需要根據不同時間不同地點不同情況對所做的應對措施進行改變，需要對整個項目的成本進行動態性控制。通過上述方法可以達到企業設定的目標成本，對此還取得良好的經濟效益和社會效益，可以看出該方法能夠可以給工程帶來良好的效果。

4 結 語

通過層次分析法把項目成本管理的風險進行劃分層次，進而建立了評價風險程度的數學模型。結合英那河工程案例可以得出層次分析法給項目成本帶來了良好的經濟效益，該法可以廣泛的應用到水利工程的項目成本管理中。

[1]曹昌平.小型水庫除險加固措施及土壩壩基帷幕灌漿的特點分析[J].水利科技與經濟，2016(02):113-115.

X913.4

C

1007-7596(2016)08-0031-04

2016-06-16

曹克元(1974-)，男，山西運城人，工程師，從事水文地質、工程地質及巖土工程勘察。