木梁拼接截面碳纖加固抗彎承載力
黃龍田,霍文斌,劉 玫
(1.廣東省建筑設計研究院,廣東 廣州 510010;2.廣州市公用事業規劃設計院,廣東 廣州 510230)
木梁拼接截面碳纖加固抗彎承載力
黃龍田1,霍文斌1,劉玫2
(1.廣東省建筑設計研究院,廣東 廣州510010;2.廣州市公用事業規劃設計院,廣東 廣州510230)
木結構矩形截面承重梁跨中拼接,拼接點沒有任何連接構造,基本上失去了抗彎能力,出于外觀的考慮,采用碳纖維片材加固,對此,導出拼接木梁極限抵抗彎矩公式。矩形截面拼接木梁用碳纖加固后彈性受力階段抗彎承載力比原材全截面計算的承載力可提高25%。界限破壞時抵抗彎矩比原材全截面計算的承載力提高約30%,提高值取決于木材受壓比例極限與屈服極限之比,即由木材性質所決定。
木結構;疊合梁;拼接截面;碳纖加固計算公式;抗彎承載力
0 引言
數座景觀木亭承重疊合梁,矩形截面,由于設計或施工的原因,梁的跨中截面由方木拼接但沒有任何連結措施(見圖1),梁已失去抗彎承載能力。
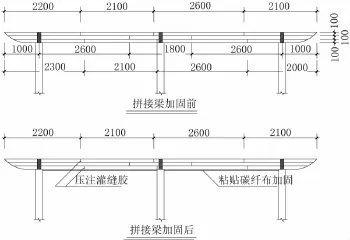
圖1 拼接梁加固前后示意圖(單位:cm)
加固方案比選結果采用碳纖維片材加固,為此要求探討和評估單根拼接木桿件經粘貼碳纖維片材加固后構件的抗彎承載力。
設定的前題是:豎向拼接面僅承受彎曲壓應力,拼接面木纖維不參加抗拉作用,彎曲拉應力完全由碳纖布所取代。以下的論述是對單根拼接木桿件而非對疊合梁,具體的加固措施另文敘述。
1 加固后梁的彎曲破壞類型
可能的破壞類型有:
(1)受壓區木材順紋擠壓破壞;
(2)碳纖布拉斷;
(3)碳纖布剝落(含粘貼區木纖維破壞)
因后兩種類型是可控的,僅對第一種破壞類型進行計算公式的分析推導。
2 基本假設
拼接截面壓注灌縫膠后受壓區可承受壓應力,不考慮受拉區粘合后的抗拉作用,截面下緣粘貼的碳纖維布作為抗拉元素;碳纖維布受拉時的應力與應變是線性關系。承載力計算公式推導的基本假設是:
(1)梁受彎后截面應變仍保持平面;
(2)碳纖的應力應變關系為線性,即
σf=Ef×εf
(3)拼接的截面只傳遞壓應力,不考慮受拉區粘合后木材的抗拉作用;
(4)碳纖布中心到梁頂的距離等于梁高;
(5)木材的應力應變關系:可通過柱形木試件測試取得[1],現按文獻資料[2]選取松木的應力應變關系曲線(見圖2)作為分析推導的基礎。
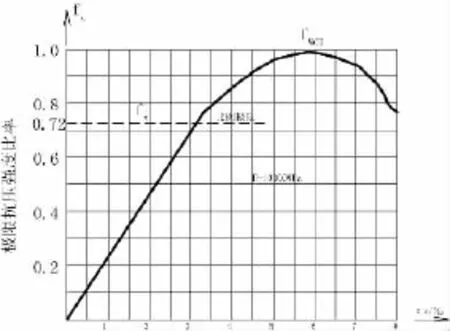
圖2 木材(松木)順紋受壓的應力應變實驗曲線
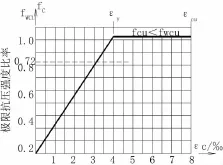
圖3 木材(松木)順紋受壓的應力--應變曲線(簡化)
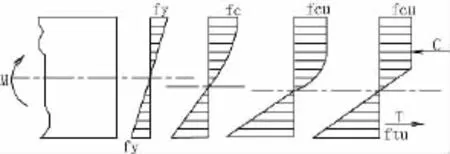
圖4 木構件受彎各工作階段
截面應力-應變關系式:
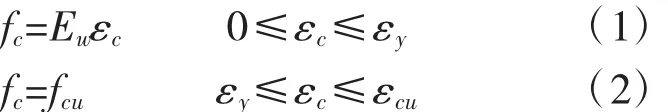
式中:fc為木材壓應力;εy為木材比例極限壓應變;εcu為木材極限壓應變;εc為木材壓應變;Ew為木材受壓彈性模量。
3 彈性受力階段截面抗彎承載力分析——實用計算方法
設定受彎構件截面應力在比例極限應力以內,木構件近似看作彈性體,外力消失后變形恢復。
彈性受力階段截面的應力分布:受壓區應力在比例極限以內,截面壓應力應變對截面形心的距離成正比,中和軸以上壓應力呈直線分布,拼接的木梁,中和軸以下截面不考慮抗拉應力,下緣碳纖拉應力與下緣應變成正比,見圖5。
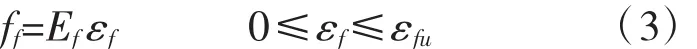
式中:εfu為碳纖極限拉應變;εf為碳纖拉應變;Ef為碳纖彈性模量;ff為碳纖拉應力。
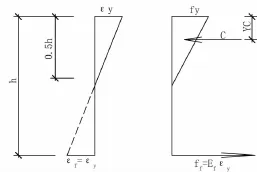
圖5 彈性受力階段截面應力分布圖
設木材比例極限壓應力為fy,受壓區壓力的合力為C,合力到截面上緣距離為yc。
C=0.25 bhfy,b為矩形截面寬度。
木結構設計規范[4]對受彎構件抗彎承載力驗算采用,fm為木材抗彎強度設計值是基于截面應變保持平面的假定和彈性體的假定,規范對fm的取值,已隱含了抗力的分項系數并經過調整,因此可按規范取fy=-fm,則受壓區壓應力合力C
C=0.25 bhfm
上式可改寫為

M0為按規范計算矩形截面梁的抗彎承載力。由∑x=0EfεfAf=C
EfεfAf=0.25bhfm
Af=0.25bhfm/Efεf
計算碳纖面積時取 εf=εY
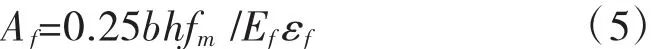
由式(4)得出,矩形拼接截面木梁用碳纖加固后抗彎承載力比原材全截面計算的承載力提高25%。條件是按式(5)計算碳纖面積,碳纖應變按小于等于木材受壓比例極限應變取值,木材抗彎強度按規范取值。
木材順紋受壓應變的比例極限εy木結構規范沒有作出規定。木材是生物材料,不同種類差異很大,比例極限可通過實驗數據取得,按文獻資料[2,5,6]對于承重結構的木材,建議可取0.002~0.004,取下限用于確定碳纖用量時將偏向安全。
對于非拼接的全截面抗彎構件加固,也可采用上述公式計算,因為沒有考慮木纖維的抗拉作用,計算結果偏于安全。
4 塑性受力階段截面抗彎承載力分析——界限破壞彎矩計算
4.1受壓區塑性變形階段的應力應變關系
木材順紋壓應力超過比例極限時,木纖維受壓屈曲,破壞時試件表面出現皺折,并呈現明顯的塑性變形特征曲線[5]。
當彎矩繼續增大,受壓區出現塑性變形,極限狀態時,壓應變εc=εcu。如果碳纖維布也同時達到最大拉應變εf=εfu,此時受壓區的高度定義為界限受壓高度,對應的彎矩定義為界限破壞彎矩。根據圖3的應力應變曲線,可以建立圖6的應變和應力圖形。
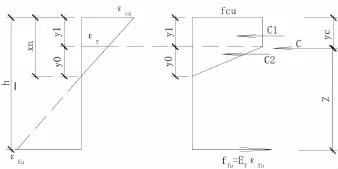
圖6 應變和應力圖
4.2界限破壞時抵抗彎矩計算
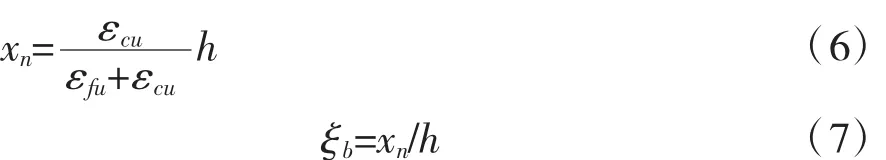
ξb:相對界限高度

取 εcu=0.008。
按加固規范[7]碳纖極限應變取εfu=0.014,則ξb=0.364。

受壓區合力c=c1+c2

合力C對受壓區上緣靜矩S:
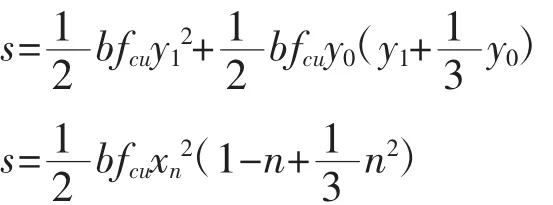
合力C重心到上緣距離yc
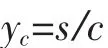
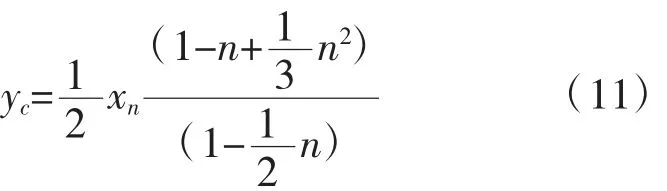
合力C對碳纖合力點取矩,則界限破壞時抵抗彎矩為:
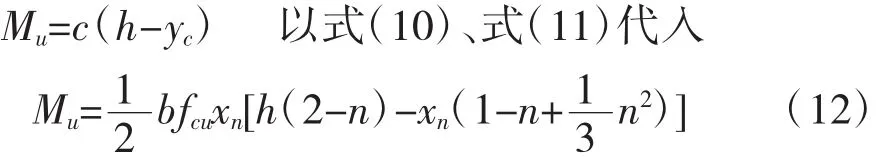
以式(7)代入
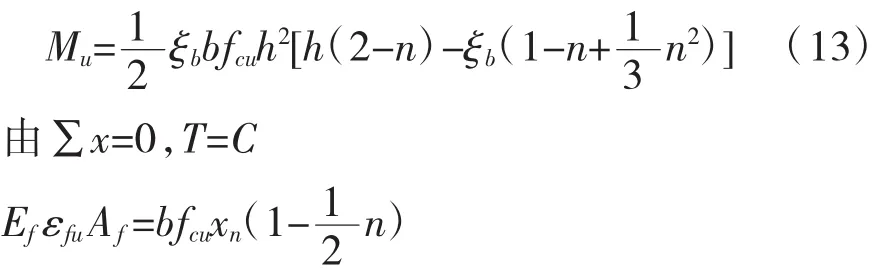
以式(7)代入
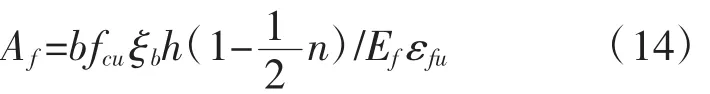
4.3小結
從以上公式可得出以下結論:
(1)當截面尺寸已定,碳纖極限應變按規范取值,界限破壞時抵抗彎矩取決于,即取決于木材受壓比例極限與屈服極限之比,由木材性質所決定。
(2)碳纖加固承載力提高的限值:式(13)可改寫為:

M0形式上相當于普通木結構計算的抗彎承載力的公式,但強度的取值為順紋抗壓極限強度計算值fcu,k1可視為粘貼碳纖后承載力提高系數。k1可制成計算表格備查(見表1)。

表1 k1系數表
k1平均值為1.30,可認為木梁碳纖加固后界限破壞時抵抗彎矩比原材按全截面計算的抵抗彎矩平均提高30%.
5 工程應用
計算理論用于某五星級賓館中庭的六座景觀木亭加固,經6 a的時間考驗,使用正常,效果良好。
[1]GB 50329-2002,木結構試驗方法標準[S].
[2]А.П.巴甫洛夫.木結構與木建筑物[M].上海:上海科學技術出版社,1961.
[3]龔偉,李希鈞,劉勵誠.鋼結構與木結構[M].北京:中國建筑出版社,1988.
[4]GB 50005-2003,木結構設計規范[S].
[5]潘景龍,祝恩淳.木結構設計原理[M].北京:中國建筑工業出版社,2009.
[6]廣西大學.木材學[Z].
[7]CECS 146:2003,碳纖維片材加固混凝土結構技術規程[S].
[8]GB 50367-2006,混凝土結構加固設計規范[S].
TU366.2
B
1009-7716(2016)06-0316-03
2016-02-23
黃龍田(1976-),男,湖南邵陽人,高級工程師,從事路橋設計工作。

