吸氣式高超聲速飛行器控制的最新研究進(jìn)展
吳立剛, 安 昊, 劉健行, 王常虹
(哈爾濱工業(yè)大學(xué) 航天學(xué)院, 哈爾濱 150001)
?
吸氣式高超聲速飛行器控制的最新研究進(jìn)展
吳立剛, 安 昊, 劉健行, 王常虹
(哈爾濱工業(yè)大學(xué) 航天學(xué)院, 哈爾濱 150001)
隨著超燃沖壓發(fā)動(dòng)機(jī)技術(shù)的快速發(fā)展, 吸氣式高超聲速飛行器正受到世界范圍內(nèi)的高度關(guān)注, 而其控制系統(tǒng)的設(shè)計(jì)則是重中之重.首先簡(jiǎn)要回顧了吸氣式高超聲速飛行器建模的發(fā)展, 表明了對(duì)其進(jìn)行控制器設(shè)計(jì)的復(fù)雜性;然后著重闡述了幾種廣泛應(yīng)用于吸氣式高超聲速飛行器的控制方法:基于線性化模型的控制方法、反向遞推法、T-S模糊控制方法、自適應(yīng)控制和滑模變結(jié)構(gòu)控制;最后指出了在控制器設(shè)計(jì)環(huán)節(jié)需要考慮的若干問題, 例如: 執(zhí)行機(jī)構(gòu)的非線性、容錯(cuò)控制、多目標(biāo)控制、切換控制等, 同時(shí)也是今后吸氣式高超聲速飛行器控制系統(tǒng)設(shè)計(jì)的研究方向.
吸氣式高超聲速飛行器;控制模型;控制系統(tǒng)設(shè)計(jì);實(shí)際問題;進(jìn)展
通常把飛行速度大于5Ma的飛行器稱為高超聲速飛行器, 由于其高速度、高機(jī)動(dòng)性、大飛行包線等優(yōu)勢(shì), 因而具有重要的民用、軍事價(jià)值和戰(zhàn)略意義.一般說(shuō)來(lái), 高超聲速飛行器主要分為兩種類型:1)火箭基高超聲速飛行器, 也稱為無(wú)動(dòng)力再入高超聲速飛行器.這類高超聲速飛行器本身不具備動(dòng)力裝置, 而是借助火箭助推器將其投送到預(yù)定的速度和高度, 然后利用自身的動(dòng)能、重力勢(shì)能以及氣動(dòng)舵面、反作用力噴氣等裝置按照預(yù)定的軌跡滑翔到最終目標(biāo), 例如: 洛克希德·馬丁公司的高超聲速技術(shù)飛行器(hypersonic technology vehicle, HTV)[1]、美國(guó)陸軍的先進(jìn)高超聲速武器(advanced hypersonic weapon, AHW)[2].2)采用吸氣式超燃沖壓發(fā)動(dòng)機(jī)作為動(dòng)力的高超聲速飛行器, 簡(jiǎn)稱吸氣式高超聲速飛行器.超燃沖壓發(fā)動(dòng)機(jī)可以在高超聲速飛行的狀態(tài)下, 使碳?xì)浠蛞簹淙剂虾臀氲目諝庠诔曀偃紵覂?nèi)進(jìn)行充分地燃燒.相比于常規(guī)的火箭發(fā)動(dòng)機(jī), 超燃沖壓發(fā)動(dòng)機(jī)不需要攜帶額外的氧化劑, 進(jìn)而有效地提升飛行器的載荷比.同時(shí), 超燃沖壓發(fā)動(dòng)機(jī)的機(jī)械結(jié)構(gòu)極其簡(jiǎn)單, 具有較低的生產(chǎn)成本和良好的可靠性.但由于超燃沖壓發(fā)動(dòng)機(jī)在低速(一般小于3.0Ma)是無(wú)法啟動(dòng)的, 因此, 這類高超聲速飛行器往往采用超燃沖壓發(fā)動(dòng)機(jī)與火箭發(fā)動(dòng)機(jī)或渦輪噴氣發(fā)動(dòng)機(jī)組合的方式, 以實(shí)現(xiàn)大范圍的全包線飛行[3].吸氣式高超聲速飛行器正得到美國(guó)、俄羅斯、英國(guó)、中國(guó)等國(guó)家的高度重視, 也是本文介紹的對(duì)象.具有代表性的吸氣式高超聲速飛行器有: 美國(guó)航空航天局的X-43A[4]、波音公司的X-51A[5]、俄羅斯的“鷹”試驗(yàn)飛行器、英國(guó)的“Shyfe”驗(yàn)證機(jī)、印度的“Avatar”空天飛機(jī)[2].
吸氣式高超聲速飛行器的研制是一項(xiàng)尖端、復(fù)雜、多學(xué)科的工程, 其涉及到高超聲速飛行動(dòng)力學(xué)、超聲速燃燒技術(shù)、熱傳導(dǎo)理論及熱防護(hù)材料、飛行器導(dǎo)航、制導(dǎo)與控制等多個(gè)學(xué)科[6-10].為了適應(yīng)高速度、高動(dòng)壓的飛行環(huán)境, 許多先進(jìn)的設(shè)計(jì)理念和制造工藝被應(yīng)用到吸氣式高超聲速飛行器的研制.例如: 扁平細(xì)長(zhǎng)的機(jī)身設(shè)計(jì)增加了飛行器的升阻比;輕質(zhì)復(fù)合材料的應(yīng)用提升了系統(tǒng)的防熱性能以及有效載荷比;機(jī)身-發(fā)動(dòng)機(jī)一體化構(gòu)型可以產(chǎn)生適于超燃沖壓發(fā)動(dòng)機(jī)工作的進(jìn)氣工況.然而, 這些先進(jìn)的技術(shù)也會(huì)給吸氣式高超聲速飛行器的控制帶來(lái)一些不期望的特性如圖1所示.例如: 細(xì)長(zhǎng)的外形設(shè)計(jì)和輕質(zhì)材料的應(yīng)用使得飛行器的機(jī)身具有更大的撓性, 在高超聲速飛行過(guò)程中極易激發(fā)彈性模態(tài), 引起機(jī)體的震動(dòng);由于超燃沖壓發(fā)動(dòng)機(jī)整合在機(jī)身下方, 因此發(fā)動(dòng)機(jī)的推力會(huì)產(chǎn)生一個(gè)附加的抬頭力矩, 增加了執(zhí)行機(jī)構(gòu)的負(fù)擔(dān);與此同時(shí), 超燃沖壓發(fā)動(dòng)機(jī)的進(jìn)氣、排氣也會(huì)對(duì)飛行器的升力、阻力和俯仰力矩產(chǎn)生嚴(yán)重的擾動(dòng).值得指出的是, 超燃沖壓發(fā)動(dòng)機(jī)對(duì)于飛行動(dòng)壓、進(jìn)氣條件以及燃空比有著相對(duì)苛刻的要求, 不當(dāng)?shù)墓r會(huì)引發(fā)所謂的熱阻現(xiàn)象, 進(jìn)而導(dǎo)致發(fā)動(dòng)機(jī)無(wú)法正常工作.可見, 吸氣式高超聲速飛行器相比于普通的飛行器而言, 具有更強(qiáng)的非線性、更復(fù)雜的耦合、更嚴(yán)重的彈性振動(dòng)以及更嚴(yán)格的控制約束[11-13].

圖1 吸氣式高超聲速飛行器控制的難點(diǎn)
Fig.1 Difficulties in the control of air-breathing hypersonic vehicles
除了吸氣式高超聲速飛行器本身的特點(diǎn), 高速、高動(dòng)壓的飛行環(huán)境也會(huì)產(chǎn)生一些不利的因素.大的飛行包線使得飛行器的飛行環(huán)境發(fā)生劇烈的變化, 又由于高超聲速氣動(dòng)熱、氣動(dòng)力的某些機(jī)理尚未明確, 因此, 目前建立的動(dòng)力學(xué)模型僅適用于某一特定的工作范圍, 并且具有很大的不確定性.高動(dòng)壓的飛行環(huán)境使得飛行器的執(zhí)行機(jī)構(gòu)(例如: 氣動(dòng)舵面)表現(xiàn)出一定的非線性特性, 甚至可能出現(xiàn)部分或者完全失效.同時(shí), 對(duì)于一些必要的飛行狀態(tài)(例如: 攻角、側(cè)滑角)很難采用已有常規(guī)的手段進(jìn)行精確測(cè)量, 例如: 空速管、慣性導(dǎo)航系統(tǒng)、嵌入式的大氣數(shù)據(jù)傳感器[14].可見, 吸氣式高超聲速飛行器控制器的設(shè)計(jì)是極具挑戰(zhàn)性的.
本文根據(jù)國(guó)內(nèi)外近期相關(guān)的成果以及作者的研究, 針對(duì)吸氣式高超聲速飛行器的控制問題進(jìn)行闡述, 并基于作者的認(rèn)知, 進(jìn)一步總結(jié)了控制器設(shè)計(jì)環(huán)節(jié)所面臨的一些實(shí)際問題.
1 吸氣式高超聲速飛行器模型概述
本文主要對(duì)于吸氣式高超聲速飛行器建模的發(fā)展做簡(jiǎn)要的概述和總結(jié).在高超聲速飛行過(guò)程中, 飛行器的幾何構(gòu)型對(duì)于飛行特性起著決定性的作用.目前, 常見的高超聲速飛行器的幾何構(gòu)型主要有帶翼錐形體構(gòu)型(winged-cone hypersonic vehicle, 如圖2(a)所示)和乘波體構(gòu)型(wave-rider hypersonic vehicle, 如圖2(b)所示).錐形體構(gòu)型的機(jī)身主體是一個(gè)軸對(duì)稱的幾何體, 由前段(圓錐體)、中段(圓柱體)、后段(圓臺(tái))3部分組成, 具有大升阻比、大細(xì)長(zhǎng)比、大后掠角以及小展弦比等特點(diǎn), 是一種比較成熟的高超聲速飛行器構(gòu)型.乘波體構(gòu)型已經(jīng)被證明是實(shí)現(xiàn)高超聲速飛行的最優(yōu)方案, 其獨(dú)特的幾何外形可使飛行器不需要額外的機(jī)翼來(lái)產(chǎn)生升力, 而是利用壓縮升力和激波升力進(jìn)行高超聲速飛行.目前, 以超燃沖壓發(fā)動(dòng)機(jī)作為動(dòng)力的高超聲速飛行器絕大部分采用乘波體構(gòu)型.其他的高超聲速飛行器構(gòu)型還有翼身融合體 (wing-body hypersonic vehicle)、升力體(lifting-body hypersonic vehicle)等.
由于吸氣式高超聲速飛行器具有非常復(fù)雜的非線性、耦合以及不確定性, 對(duì)其建立精準(zhǔn)的數(shù)學(xué)模型是極為困難的, 因此, 目前相關(guān)建模的研究主要集中于縱向、剛體動(dòng)力學(xué)建模[15-17].Chavez等[18]首次采用牛頓碰撞理論建立了可分析的超燃沖壓發(fā)動(dòng)機(jī)以及吸氣式高超聲速飛行器的數(shù)學(xué)模型. Shaughnessy等[19]利用風(fēng)洞實(shí)驗(yàn)測(cè)量氣動(dòng)力、力矩系數(shù)在不同攻角、速度和氣動(dòng)舵偏角下的數(shù)值, 為一類帶翼錐形體構(gòu)型的高超聲速飛行器建立了縱向剛體運(yùn)動(dòng)模型.Marrison等[20]進(jìn)一步在特定平衡點(diǎn)處得到其簡(jiǎn)化的擬合形式, 這個(gè)模型在早期的高超聲速飛行控制中得到了廣泛的應(yīng)用[21].近期, Bolender等[22]利用斜波理論和普朗特-邁耶?dāng)U張理論對(duì)于文獻(xiàn)[18]的工作進(jìn)行了發(fā)展和改進(jìn), 構(gòu)建了一類乘波體構(gòu)型的高超聲速飛行器的縱向彈性體運(yùn)動(dòng)模型.該模型可以很好地捕捉到超燃沖壓發(fā)動(dòng)機(jī)、空氣動(dòng)力學(xué)、結(jié)構(gòu)動(dòng)力學(xué)之間的關(guān)系.Parker等[23]進(jìn)一步利用多項(xiàng)式擬合的方法對(duì)于文獻(xiàn)[22]提出的模型進(jìn)行簡(jiǎn)化處理, 得到了面向控制器設(shè)計(jì)的吸氣式高超聲速飛行器模型(control-oriented model, COM).為方便后文的闡述, 以下總結(jié)了幾種具有代表性的數(shù)學(xué)模型.
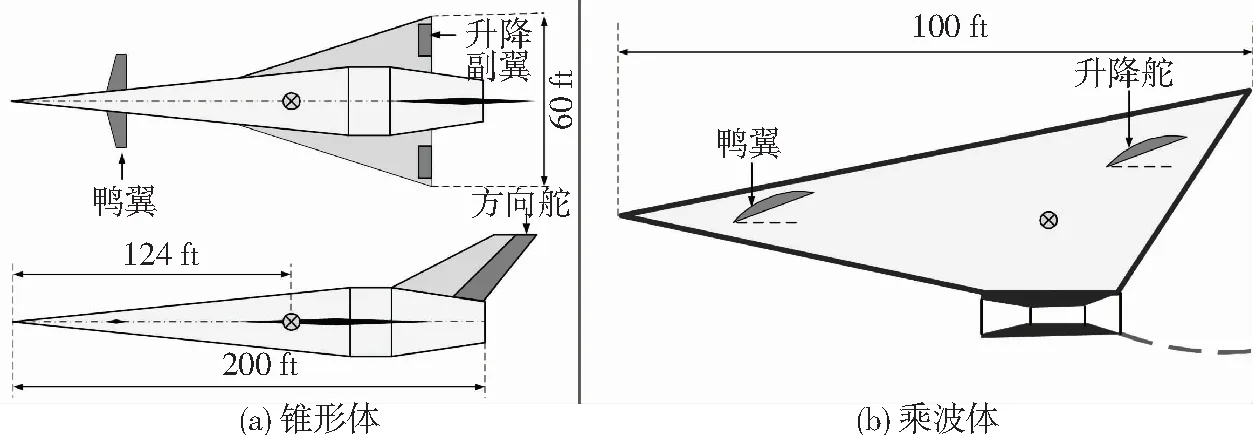
圖2 兩種常見的高超聲速飛行器構(gòu)型
1.1 錐形體縱向運(yùn)動(dòng)擬合模型
錐形體構(gòu)型的高超聲速飛行器(如圖2(a)所示)的縱向運(yùn)動(dòng)剛體動(dòng)力學(xué)方程為[20]
(1)
其中推力T、升力L、阻力D、俯仰力矩Myy有如下表達(dá)式:
(2)
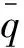
(3)
式中α0為平衡點(diǎn)處的攻角值.上述吸氣式高超聲速飛行器的數(shù)學(xué)模型(1)~(3)包含5個(gè)剛體飛行狀態(tài)量: 速度V、高度h、飛行航跡角γ、飛行攻角α、俯仰角速率Q;兩個(gè)控制輸入量: 燃料節(jié)流閥控制量δT、升降舵偏轉(zhuǎn)角δe.該模型并沒有考慮機(jī)身的彈性模態(tài)、超燃沖壓發(fā)動(dòng)機(jī)與機(jī)身之間的耦合以及氣動(dòng)舵偏轉(zhuǎn)角對(duì)于氣動(dòng)力(升力和阻力)的影響, 因此對(duì)于吸氣式高超聲速飛行器動(dòng)態(tài)特性的描述十分有限.即便如此, 其數(shù)學(xué)表達(dá)式仍是十分復(fù)雜的.
1.2 乘波體縱向運(yùn)動(dòng)擬合模型
乘波體構(gòu)型的高超聲速飛行器的縱向運(yùn)動(dòng)剛體動(dòng)力學(xué)方程與式(1)是相同的, 其彈性體模型具有如下表達(dá)式(僅為一種簡(jiǎn)單的表達(dá)形式, 詳見文獻(xiàn)[23-24]):
(4)
式中: 0<ξi<1,ωi>0為常數(shù).推力T、升力L、阻力D、俯仰力矩Myy以及廣義力Ni可以通過(guò)如下多項(xiàng)式擬合得到:
(5)
1.3 線性參數(shù)變化系統(tǒng)模型
基于乘波體縱向運(yùn)動(dòng)擬合模型, 文獻(xiàn)[25]進(jìn)一步推導(dǎo)出與之對(duì)應(yīng)的線性變參數(shù)模型(linearparameter-varyingmodel,LPVM), 該模型可以應(yīng)用于增益調(diào)度控制 (gain-schedulingcontrol,GSC) 或者基于線性不等式的魯棒控制 (LMI-basedrobustcontrol,LMI-BRC) 等, 其表達(dá)式具有如下線性形式:
(6)
1.4 六自由度模型
利用動(dòng)力學(xué)基本原理, 可以推導(dǎo)出吸氣式高超聲速飛行器的六自由度模型(6 degrees of freedom model, 6-DOFM)如下:
(7)
(8)
(9)
(10)
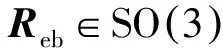
需要說(shuō)明的是, 模型(7)~(10)僅給出了高超聲速飛行器六自由度運(yùn)動(dòng)模型的整體框架, 相關(guān)的力/力矩表達(dá)式還需要進(jìn)行復(fù)雜的近似擬合處理, 所得到的擬合模型具有極其復(fù)雜的形式, 因此, 該六自由度模型常被用作控制算法的計(jì)算機(jī)仿真驗(yàn)證模型.通過(guò)進(jìn)行必要的假設(shè)(如慣量矩陣J為對(duì)角陣)并且合理地忽略一些耦合(如忽略氣動(dòng)舵面產(chǎn)生的附加阻力), 可以得到面向控制器設(shè)計(jì)的六自由度運(yùn)動(dòng)模型.例如, 文獻(xiàn)[26]進(jìn)一步采用克里金法(kriging method)和最小二乘法(least square method)對(duì)于氣動(dòng)力/力矩進(jìn)行擬合, 擬合后的模型可用于制導(dǎo)律、控制器的設(shè)計(jì).
本文概述了高超聲速飛行器控制中常用的4種數(shù)學(xué)模型, 實(shí)際的控制器設(shè)計(jì)不僅僅局限于這些模型, 例如將要介紹的精確線性化模型以及T-S模糊模型.可以看出, 錐形體、乘波體模型均為描述高超聲速飛行器縱向運(yùn)動(dòng)的非線性模型, 反映了高超聲速飛行的本質(zhì)屬性, 但其表達(dá)形式十分復(fù)雜.而線性變參數(shù)模型以及以下將要給出的反饋線性化模型、T-S模糊模型則是在上述兩種非線性模型的基礎(chǔ)上, 采用一定的模型處理方法而得到的具有一定線性形式的高超聲速飛行器模型, 這類模型雖然易于控制器設(shè)計(jì), 但仍有一定的不足, 例如: 反饋線性化模型完全抵消了原系統(tǒng)的非線性, T-S模糊模型的建立則需要具備充分的經(jīng)驗(yàn).六自由度模型僅僅給出了基本的運(yùn)動(dòng)學(xué)、動(dòng)力學(xué)方程以及執(zhí)行機(jī)構(gòu)的非線性, 具體的力、力矩還需要大量的理論分析及風(fēng)洞試驗(yàn)進(jìn)行確定.表1對(duì)各個(gè)模型的特點(diǎn)及用途進(jìn)行了簡(jiǎn)要的總結(jié).值得指出的是, 目前大部分對(duì)于吸氣式高超聲速飛行器控制的研究局限于縱向運(yùn)動(dòng), 并且忽略彈性模態(tài)(4), 僅對(duì)剛體動(dòng)力學(xué)(1)進(jìn)行控制系統(tǒng)的設(shè)計(jì).即便如此, 所要考慮的數(shù)學(xué)模型仍是十分復(fù)雜的, 往往需要結(jié)合多種線性、非線性控制理論來(lái)進(jìn)行控制器的綜合設(shè)計(jì).
2 吸氣式高超聲速飛行器的控制方法
一般來(lái)說(shuō), 在實(shí)施高超聲速飛行器控制器設(shè)計(jì)之前, 首先需要對(duì)其復(fù)雜的數(shù)學(xué)模型進(jìn)行預(yù)處理, 然后利用適當(dāng)?shù)目刂品椒ㄟM(jìn)行控制器的設(shè)計(jì).本文以高超聲速飛行器模型的處理手段為分類準(zhǔn)則, 闡述了3大類控制構(gòu)型: 基于線性化模型的控制、基于非線性模型的反向遞推控制以及基于T-S模糊模型的控制.進(jìn)而可以利用以上3種構(gòu)型并結(jié)合不同的控制方法進(jìn)行控制器的設(shè)計(jì),最后舉例說(shuō)明了兩種被廣泛應(yīng)用的控制方法: 自適應(yīng)控制與滑模變結(jié)構(gòu)控制.
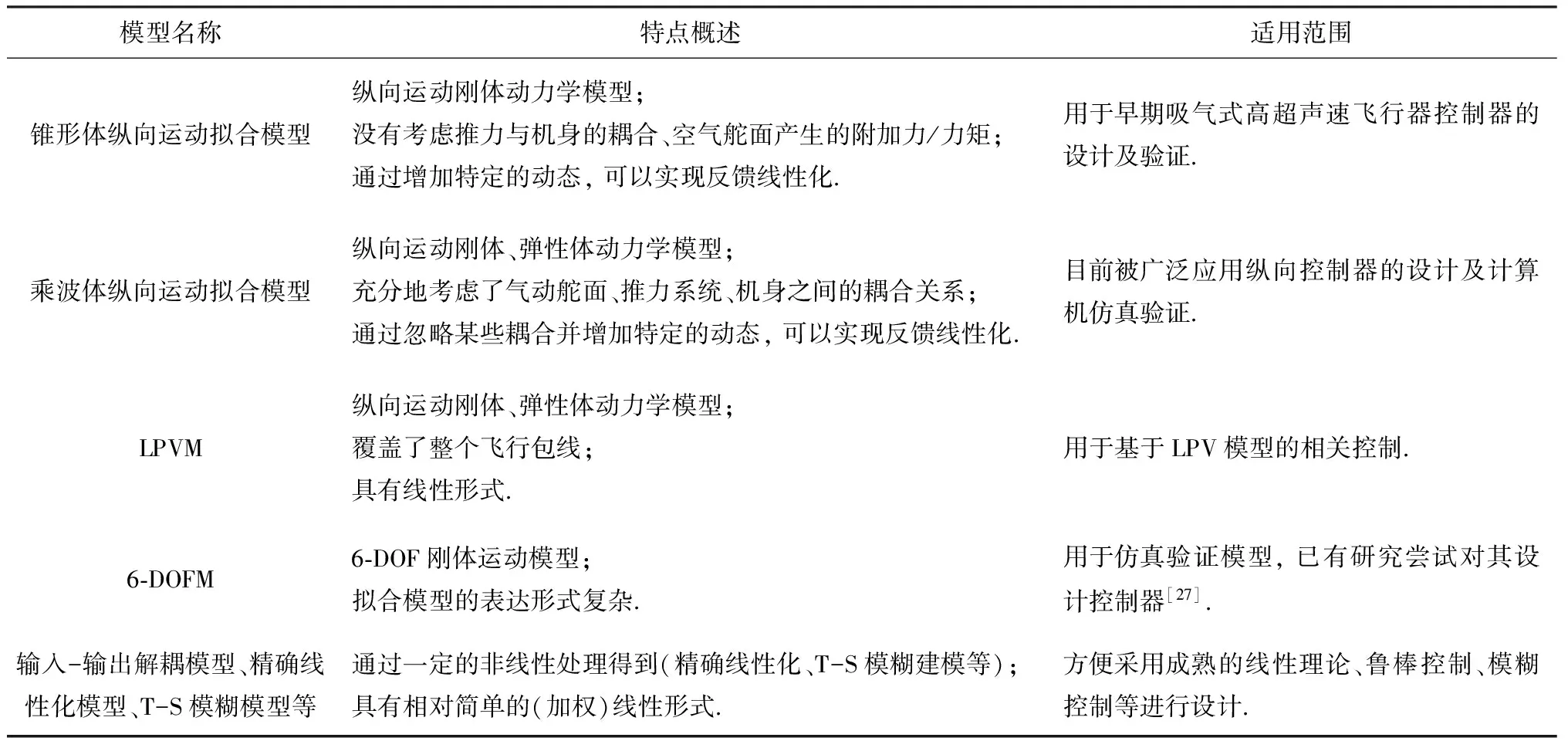
表1 吸氣式高超聲速飛行器模型總結(jié)
2.1 模型線性化控制
模型線性化控制的基本思想為: 首先采用一定的手段, 將吸氣式高超聲速飛行器的非線性模型進(jìn)行線性化處理, 然后利用適當(dāng)?shù)目刂评碚搶?duì)于得到的線性模型進(jìn)行控制器設(shè)計(jì), 最終的控制器由模型線性化部分和線性模型控制律組成, 如圖3所示.雖然平衡點(diǎn)處小偏差線性化方法也可以應(yīng)用于高超聲速飛行器模型, 但是對(duì)于大范圍的機(jī)動(dòng)來(lái)說(shuō), 采用這種方法并不適用.
在高超聲速飛行控制中, 常用的線性化手段主要有動(dòng)態(tài)逆補(bǔ)償(dynamic inverse compensation, DIC)和反饋線性化(feedback linearization, FL).動(dòng)態(tài)逆補(bǔ)償?shù)幕舅枷胧窃O(shè)計(jì)一個(gè)逆系統(tǒng)來(lái)抵消系統(tǒng)中的非線性動(dòng)態(tài), 進(jìn)而得到相應(yīng)的偽線性系統(tǒng).反饋線性化則利用微分幾何理論和Lie導(dǎo)數(shù)等工具, 對(duì)于滿足一定條件的系統(tǒng)模型通過(guò)反饋控制實(shí)現(xiàn)輸入-輸出解耦, 在特定的坐標(biāo)系下, 原非線性模型可以轉(zhuǎn)化為具有標(biāo)準(zhǔn)形式的線性模型.
例如, 文獻(xiàn)[23]首先對(duì)于乘波體縱向運(yùn)動(dòng)擬合模型進(jìn)行如下假設(shè):
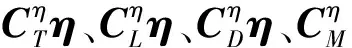
2)鴨翼的偏轉(zhuǎn)抵消了升降舵偏角對(duì)于升力的影響, 并且忽略升降舵產(chǎn)生的附加阻力, 進(jìn)而系統(tǒng)是最小相位的;
然后利用坐標(biāo)進(jìn)行變換:
以及反饋控制律:
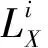
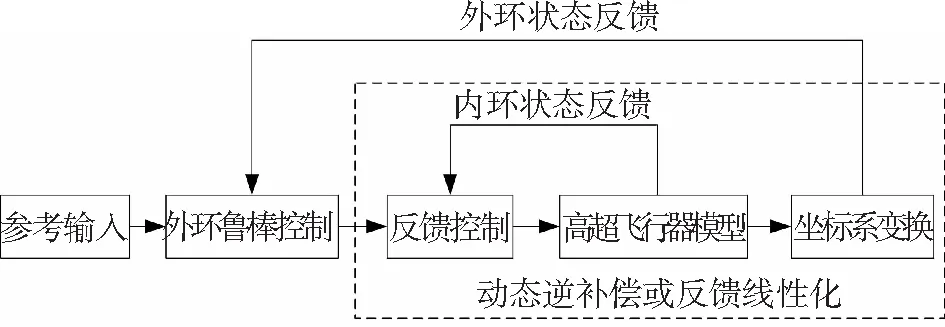
圖3 高超聲速飛行器模型線性化控制的基本結(jié)構(gòu)
Fig.3Structureofthelinearizedmodel-basedcontrolforair-breathinghypersonicvehicles
動(dòng)態(tài)逆補(bǔ)償和反饋線性化都面臨一個(gè)共同的問題[28]: 由于吸氣式高超聲速飛行器模型的非線性部分并不能精確已知, 即存在建模的不確定性[29], 因此, 在模型線性化過(guò)程中必然會(huì)產(chǎn)生相應(yīng)的逆誤差或反饋誤差.這就要求所設(shè)計(jì)的控制器在保證控制精度的同時(shí), 還需具備一定的魯棒性來(lái)克服線性化誤差.針對(duì)具有一定不確定性的吸氣式高超聲速飛行器模型, 文獻(xiàn)[30]采用魯棒反饋線性化方法推導(dǎo)出一種面向控制的線性不確定性模型(control-oriented linearized uncertainty model, CLUM):
(11)
模型線性化控制方法在吸氣式高超聲速飛行器控制領(lǐng)域已有較為廣泛的應(yīng)用.文獻(xiàn)[21]利用動(dòng)態(tài)逆補(bǔ)償將高超聲速飛行器模型進(jìn)行線性化, 針對(duì)建模存在的參數(shù)不確定性, 利用隨機(jī)魯棒控制理論進(jìn)行反饋控制律的設(shè)計(jì);文獻(xiàn)[30]基于魯棒反饋線性化模型(11)設(shè)計(jì)了極大-極小線性二次型輸出跟蹤魯棒控制器;文獻(xiàn)[31]利用反饋線性化和線性二次型高斯調(diào)節(jié)器, 實(shí)現(xiàn)了具有彈性模態(tài)和輸入耦合的吸氣式高超聲速飛行器的跟蹤控制;文獻(xiàn)[32]首先對(duì)可能存在執(zhí)行機(jī)構(gòu)故障的吸氣式高超聲速飛行器模型進(jìn)行反饋線性化, 并得到其線性模型, 然后利用滑模觀測(cè)器設(shè)計(jì)自適應(yīng)控制律來(lái)實(shí)現(xiàn)飛行速度、高度的精確跟蹤, 并具備一定的容錯(cuò)能力.
模型線性化控制方法的主要優(yōu)勢(shì)在于克服了高超聲速飛行器模型的復(fù)雜性, 同時(shí), 可以將成熟的線性控制理論引入到高超聲速飛行器的控制問題當(dāng)中.需要指出的是, 基于模型線性化的控制方法主要存在兩點(diǎn)不足: 1) 為了使吸氣式高超聲速飛行器模型滿足精確線性化條件, 需要適當(dāng)?shù)卦黾觿?dòng)態(tài)并忽略一些非線性特征及弱耦合項(xiàng);2) 線性化過(guò)程抵消了一些有益的非線性, 造成執(zhí)行機(jī)構(gòu)效能的浪費(fèi).可見, 模型線性化方法雖然簡(jiǎn)化了控制器的設(shè)計(jì), 但實(shí)際的應(yīng)用仍有諸多制約.因此, 更為廣泛、有效的方法是直接針對(duì)吸氣式高超聲速飛行器的非線性模型進(jìn)行控制器的設(shè)計(jì), 例如將要介紹的反向遞推法.
2.2 反向遞推控制
反向遞推法(back-stepping)是一種應(yīng)用廣泛的基于Lyapunov函數(shù)的非線性綜合設(shè)計(jì)方法.該方法首先將系統(tǒng)分為若干個(gè)串聯(lián)的子系統(tǒng), 然后從包含輸出的子系統(tǒng)到包含輸入的子系統(tǒng)依次設(shè)計(jì)虛擬控制律, 并最終得到執(zhí)行機(jī)構(gòu)的控制指令[33].由于反向遞推法可以在每一步充分地考慮系統(tǒng)的非線性, 并且設(shè)計(jì)過(guò)程自然地保持了系統(tǒng)的穩(wěn)定性, 因此, 在吸氣式高超聲速飛行器控制領(lǐng)域應(yīng)用較為廣泛.
對(duì)于吸氣式高超聲速飛行器縱向運(yùn)動(dòng)的剛體動(dòng)力學(xué)模型(1), 本文可以將其拆分成3個(gè)子系統(tǒng): 速度子系統(tǒng) (第1個(gè)動(dòng)態(tài)方程)、高度子系統(tǒng) (第2和第3個(gè)動(dòng)態(tài)方程)、姿態(tài)子系統(tǒng) (第4和第5個(gè)動(dòng)態(tài)方程), 如圖4所示, 然后依次對(duì)這3個(gè)子系統(tǒng)采用適當(dāng)?shù)姆蔷€性理論進(jìn)行控制律的設(shè)計(jì).反向遞推法的標(biāo)準(zhǔn)設(shè)計(jì)步驟在許多文獻(xiàn)及教材中均有詳細(xì)的介紹, 這里不再贅述.需要說(shuō)明的是, 雖然鴨翼的引入消除了系統(tǒng)的非最小相位特性、進(jìn)而簡(jiǎn)化了控制器的設(shè)計(jì)難度, 但是增加了飛行器機(jī)構(gòu)的復(fù)雜性以及熱防護(hù)系統(tǒng)的負(fù)擔(dān), 因此, 有些控制方法采用非線性理論來(lái)克服系統(tǒng)的非最小相位特性[34].另外, 吸氣式高超聲速飛行器的彈性動(dòng)力學(xué)(4)與剛體動(dòng)力學(xué)(1)之間是相互耦合的, 但目前的控制器設(shè)計(jì)很少考慮到機(jī)體的彈性模態(tài), 比較普遍的處理方法是將其對(duì)于剛體動(dòng)力學(xué)的影響等價(jià)為滿足特定條件的外界擾動(dòng).
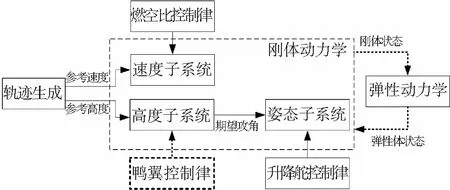
圖4 高超聲速飛行器反向遞推法控制的基本結(jié)構(gòu)
Fig.4 Structure of the back-stepping design for air-breathing hypersonic vehicles
基于上述構(gòu)型, 很多非線性控制理論可以應(yīng)用于子系統(tǒng)控制律的設(shè)計(jì).針對(duì)吸氣式高超聲速飛行器模型中的彈性模態(tài)和參數(shù)不確定性, 文獻(xiàn)[24]采用反向遞推和自適應(yīng)控制理論進(jìn)行魯棒控制器的設(shè)計(jì), 并證明了可以通過(guò)選擇適當(dāng)?shù)目刂茀?shù)來(lái)實(shí)現(xiàn)輸出的漸進(jìn)跟蹤以及對(duì)于彈性模態(tài)的抑制;文獻(xiàn)[34]結(jié)合自適應(yīng)控制理論、小增益參數(shù)和反向遞推設(shè)計(jì)方法, 僅利用燃空比和升降舵作為系統(tǒng)輸入, 實(shí)現(xiàn)了輸出的跟蹤控制, 克服了吸氣式高超聲速飛行器的非最小相位特性;文獻(xiàn)[35]針對(duì)非匹配不確定擾動(dòng)采用反向遞推與非線性擾動(dòng)觀測(cè)器相結(jié)合的方法, 為吸氣式高超聲速飛行器設(shè)計(jì)了追蹤控制器;文獻(xiàn)[36]利用自適應(yīng)動(dòng)態(tài)面與反向遞推的設(shè)計(jì)方法, 克服了執(zhí)行機(jī)構(gòu)的約束和不確定性.實(shí)際上, 反向遞推法還可以與其他非線性理論相結(jié)合進(jìn)行控制器設(shè)計(jì), 例如: 神經(jīng)網(wǎng)絡(luò)控制[37-38], 但限于篇幅限制這里不再列舉.
反向遞推法設(shè)計(jì)的優(yōu)勢(shì)在于可以充分考慮高超聲速飛行器模型的動(dòng)態(tài)特性: 在抵消有害非線性的同時(shí), 將一些有利于系統(tǒng)穩(wěn)定的非線性加以利用, 進(jìn)而減少了所設(shè)計(jì)的高超聲速飛行控制器的保守性.但反向遞推法相對(duì)于其他方法而言, 其設(shè)計(jì)過(guò)程略顯繁瑣.尤其當(dāng)設(shè)計(jì)的步數(shù)較多時(shí), 對(duì)于虛擬控制的高階求導(dǎo)會(huì)生成大量的分析計(jì)算, 所得到的控制律形式也極為復(fù)雜[33].這個(gè)問題可以通過(guò)利用指令濾波器[39]或者其他形式的微分器加以解決[40].
2.3 T-S模糊控制
除了動(dòng)態(tài)逆補(bǔ)償和反饋線性化, 設(shè)計(jì)者還可以采用一些智能控制理論來(lái)充分逼近模型的動(dòng)態(tài)特性, 從而避免了繁雜的非線性分析, 例如神經(jīng)網(wǎng)絡(luò)控制、模糊控制等.這里著重闡述一種比較成熟的智能控制方法: T-S模糊控制(Takagi-Sugeno fuzzy control, T-S FC).T-S模糊控制的基本思想是: 首先通過(guò)一定的模糊規(guī)則將吸氣式高超聲速飛行器的非線性模型近似為一系列線性子系統(tǒng)的加權(quán)形式, 即T-S模糊建模, 然后利用并行分布補(bǔ)償(parallel-distributed compensation, PDC)原理設(shè)計(jì)并得到最終的控制律.采用T-S模糊控制的非線性系統(tǒng)的穩(wěn)定性可以利用線性矩陣不等式(linear matrix inequality, LMI)等工具加以證明, 如圖5所示.以文獻(xiàn)[41]為例, 說(shuō)明吸氣式高超聲速飛行器T-S模糊建模的方法.
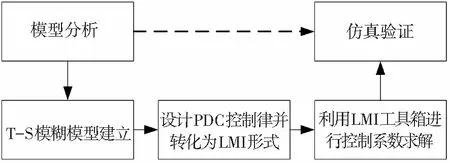
圖5 高超聲速飛行器T-S模糊控制器的設(shè)計(jì)步驟
Fig.5 Design steps of the T-S fuzzy controller for air-breathing hypersonic vehicles
首先, 注意到速度V和攻角α對(duì)于乘波體縱向運(yùn)動(dòng)擬合模型有重要影響, 本文將V和α作為兩個(gè)前提變量, 并定義模糊子集:S={Small, Middle, Big}和模糊隸屬函數(shù)(以V為例):
If V≥VM,
If V 式中:VS、VB、VM分別為速度在可行域的下界(Small)、上界(Big)和一個(gè)平衡點(diǎn)(Middle);攻角的隸屬度函數(shù)也有類似的形式. 然后, 得到如下9(32)條模糊規(guī)則: Rule (i): IfVis Small (or Middle or Big),αis Small (or Middle or Big), then: 式中: i=1,2,…,9;x、u分別為系統(tǒng)狀態(tài)向量、輸入向量;Ai、Bi分別可以通過(guò)特定的算法得到;C為輸出矩陣.從而吸氣式高超聲速飛行器T-S模糊模型具有如下形式: (12) 在得到T-S模糊模型(12)之后, 本文可以采用并行分布補(bǔ)償?shù)姆椒ㄟM(jìn)行控制器設(shè)計(jì), 并應(yīng)用線性矩陣不等式工具求解使閉環(huán)系統(tǒng)滿足穩(wěn)定性條件以及特定性能指標(biāo)的控制參數(shù), 限于篇幅這里不再贅述.利用上述T-S模糊控制方法, 文獻(xiàn)[41]為吸氣式高超聲速飛行器設(shè)計(jì)了保性能控制器, 即: 在實(shí)現(xiàn)輸出跟蹤的同時(shí),還滿足了一定的性能指標(biāo), 最終控制器參數(shù)滿足的條件以線性矩陣不等式的形式給出, 可以利用標(biāo)準(zhǔn)的數(shù)學(xué)軟件(如Matlab的LMI工具箱)進(jìn)行求解;文獻(xiàn)[42]考慮了執(zhí)行機(jī)構(gòu)和傳感器出現(xiàn)故障的情形, 采用T-S模糊控制方法設(shè)計(jì)了容錯(cuò)控制器;文獻(xiàn)[43]將滑模變結(jié)構(gòu)控制理論與T-S模糊建模相結(jié)合, 進(jìn)一步考慮了執(zhí)行機(jī)構(gòu)的飽和、死區(qū)等非線性特性;文獻(xiàn)[44]利用T-S模糊控制實(shí)現(xiàn)了吸氣式高超聲速飛行器的動(dòng)態(tài)輸出反饋控制. 基于T-S模糊模型的控制器設(shè)計(jì)的優(yōu)勢(shì)在于可以利用簡(jiǎn)單的線性形式去逼近高超聲速飛行器復(fù)雜的飛行動(dòng)態(tài), 甚至可以考慮機(jī)身的彈性動(dòng)力學(xué)(需要說(shuō)明的是, 精確線性化方法目前還難以考慮高超聲速飛行器的彈性模態(tài)), 同時(shí)也有較為成熟的理論去證明閉環(huán)系統(tǒng)的穩(wěn)定性.T-S模糊建模雖然簡(jiǎn)化了控制器的設(shè)計(jì)過(guò)程, 但也存在不足: 1)隨著模糊規(guī)則的增加, 系統(tǒng)的設(shè)計(jì)過(guò)程會(huì)變得更加復(fù)雜;2)隸屬函數(shù)的選取需要一定的經(jīng)驗(yàn);3)T-S模糊控制方法通常只能給出滿足穩(wěn)定性和性能指標(biāo)的控制器參數(shù)的充分條件. 2.4 自適應(yīng)控制和滑模變結(jié)構(gòu)控制 以上總結(jié)了3種高超聲速飛行器常用的控制構(gòu)型: 模型線性化、反向遞推以及T-S模糊控制.基于此, 許多控制理論可以與之相結(jié)合進(jìn)行控制器的設(shè)計(jì).這里主要介紹兩種廣泛應(yīng)用的控制方法: 自適應(yīng)控制和滑模變結(jié)構(gòu)控制. 2.4.1 自適應(yīng)控制 由于吸氣式高超聲速飛行器的模型參數(shù)存在嚴(yán)重的不確定性, 因此, 自適應(yīng)理論在飛行控制中有著較為廣泛的應(yīng)用, 主要體現(xiàn)在兩個(gè)方面: 1) 不確定參數(shù)的辨識(shí). 2) 自適應(yīng)跟蹤控制.參數(shù)辨識(shí)是高超聲速飛行器研究領(lǐng)域的一個(gè)重要課題, 例如:X-43A在飛行試驗(yàn)的最后階段進(jìn)行了一系列的機(jī)動(dòng)飛行, 進(jìn)而成功地辨識(shí)出特定的未知參數(shù), 為進(jìn)一步分析高超聲速飛行的動(dòng)態(tài)特性以及設(shè)計(jì)高性能的控制器獲取了必要的條件.但參數(shù)辨識(shí)問題不是本文研究的重點(diǎn), 因此, 以下主要對(duì)于自適應(yīng)跟蹤控制問題進(jìn)行闡述. 由于自適應(yīng)控制對(duì)系統(tǒng)不確定性(尤其是參數(shù)不確定性)具有強(qiáng)大的處理能力, 因此, 在吸氣式高超聲速飛行器跟蹤控制中已有著廣泛的應(yīng)用, 例如文獻(xiàn)[24, 27, 34, 45-46].以反向遞推方法中的速度子系統(tǒng)(如圖4所示)為例, 簡(jiǎn)要說(shuō)明自適應(yīng)控制的設(shè)計(jì)過(guò)程. 考慮速度動(dòng)態(tài)方程(1) 以及推力T、阻力D的擬合方程(5), 并假設(shè): 1)推力和阻力表達(dá)式中的擬合系數(shù)為未知的常值; (13) 其中Vr為速度參考軌跡, 并且 對(duì)于線性參數(shù)化方程(13), 可以設(shè)計(jì)控制律: 和自適應(yīng)律: 由上述例子可以看出, 自適應(yīng)控制的優(yōu)勢(shì)在于可以很好地處理高超聲速飛行器的參數(shù)不確定性, 這也是高超聲速飛行控制中所面臨的重要的問題之一, 另外, 由于自適應(yīng)控制方法具有強(qiáng)大的在線估計(jì)能力, 其也可用于高超聲速飛行器的參數(shù)辨識(shí)、故障檢測(cè)與處理等問題, 是目前應(yīng)用最為廣泛的高超聲速飛行控制手段.但需要說(shuō)明的是: 1) 自適應(yīng)跟蹤控制器中的估計(jì)參數(shù)一般并不收斂到其真實(shí)值, 這是由于輸入信號(hào)的“持續(xù)激勵(lì)”條件[47]在實(shí)際的跟蹤控制問題中是無(wú)法滿足的(例如, 一般會(huì)設(shè)定比較平緩的參考軌跡Vr, 以避免劇烈的機(jī)動(dòng)飛行);2) 除了參數(shù)不確定性, 還需進(jìn)一步考慮其他的約束條件, 例如: 燃空比的上、下限、氣動(dòng)舵的最大偏轉(zhuǎn)角、終端約束、高超聲速飛行走廊(hypersonic corridor)等. 2.4.2 滑模變結(jié)構(gòu)控制 一般來(lái)說(shuō), 直接針對(duì)高超聲速飛行器復(fù)雜的非線性模型進(jìn)行滑模面、趨近律的設(shè)計(jì)是非常困難的, 因此需要對(duì)于非線性模型進(jìn)行預(yù)處理.例如, 針對(duì)具有特定不確定性及外界擾動(dòng)的吸氣式高超聲速飛行器模型, 利用模型線性化控制中的假設(shè)并對(duì)跟蹤輸出(即速度V和高度h)反復(fù)地進(jìn)行求導(dǎo)運(yùn)算, 可以得到如下形式的表達(dá)式: (14) 首先, 對(duì)于具有參數(shù)不確定性和擾動(dòng)項(xiàng)的吸氣式高超聲速飛行器模型進(jìn)行T-S模糊建模.利用與T-S模糊控制相同的模糊集合與隸屬度函數(shù), 定義如下9(32)條模糊規(guī)則: Rule(i):IfVisSmall(orMiddleorBig),αisSmall(orMiddleorBig),then: 然后, 對(duì)應(yīng)每個(gè)模糊規(guī)則定義如下參考模型: Rule(i):IfVisSmall(orMiddleorBig), αisSmall(orMiddleorBig),then: Rule(i):IfVisSmall(orMiddleorBig), αisSmall(orMiddleorBig),then: 式中: Gi∈R2×7, Ki∈R2×7為需要設(shè)計(jì)的常值矩陣.因此, 整個(gè)系統(tǒng)的滑模面函數(shù)可以表示為 本文主要闡述了吸氣式高超聲速飛行器3種常見的控制構(gòu)型: 基于模型線性化的設(shè)計(jì)方法、反向遞推設(shè)計(jì)方法、T-S模糊控制方法, 并舉例說(shuō)明自適應(yīng)控制、滑模變結(jié)構(gòu)控制在高超聲速飛行控制領(lǐng)域的應(yīng)用.總的來(lái)說(shuō), 模型線性化方法雖然簡(jiǎn)化了控制器設(shè)計(jì), 卻忽略了吸氣式高超聲速飛行器的一些重要非線性(如非最小相位特性), 限制了其在實(shí)際工程中的應(yīng)用;反向遞推法和T-S模糊控制方法雖然設(shè)計(jì)步驟略顯繁瑣,但具有強(qiáng)大的非線性處理能力和良好的控制性能, 因此也是目前比較主流的設(shè)計(jì)方法;自適應(yīng)控制可以有效地處理飛行器建模產(chǎn)生的不確定性, 在實(shí)際的飛行試驗(yàn)中(如X-43A, HIFiRE項(xiàng)目等)已有應(yīng)用;而滑模變結(jié)構(gòu)控制具有較強(qiáng)的魯棒性和適應(yīng)性, 并且可以達(dá)到優(yōu)異的控制性能(如有限時(shí)間收斂), 其應(yīng)用前景十分廣闊.當(dāng)然, 吸氣式高超聲速飛行器的控制方法遠(yuǎn)不止這些, 例如, 神經(jīng)網(wǎng)絡(luò)控制(neural networks control, NNC), 軌跡線性化控制(trajectory linearization control, TLC), 線性變參數(shù)控制(linear parameter varying control, LPVC)等.無(wú)論采用何種方法進(jìn)行控制器的設(shè)計(jì), 都需要充分考慮實(shí)際系統(tǒng)自身的特點(diǎn), 因此, 以下將進(jìn)一步討論吸氣式高超聲速飛行器控制中需要解決的實(shí)際問題. 3.1 執(zhí)行機(jī)構(gòu)的非線性 針對(duì)吸氣式高超聲速飛行器氣動(dòng)舵面的飽和、死區(qū)等非線性的控制器設(shè)計(jì)已經(jīng)獲得較多的關(guān)注, 例如: 文獻(xiàn)[36-37, 39, 43, 55-56].實(shí)際的執(zhí)行機(jī)構(gòu)還可能存在一些更為復(fù)雜的動(dòng)態(tài)非線性特性, 這里著重介紹兩種常見的、但未在高超聲速飛行控制中充分考慮的非線性特性: 齒隙非線性和延遲特性. 氣動(dòng)舵面的機(jī)械連接以及伺服機(jī)構(gòu)的電氣特性會(huì)產(chǎn)生齒隙非線性(backlashnonlinearity).齒隙非線性的數(shù)學(xué)描述為[57] (15) 式中:uI、uO分別為齒隙非線性的輸入和輸出;KB>0,Br>0,Bl>0為未知常數(shù).由表達(dá)式(15)可以看出: 齒隙特性是控制輸入及其導(dǎo)數(shù)的函數(shù), 因此, 對(duì)這類非線性執(zhí)行機(jī)構(gòu)進(jìn)行理論分析以及控制器設(shè)計(jì)會(huì)更為復(fù)雜. 齒隙非線性特性(15)可以寫成如下線性形式: 另外一種更為有效的方法是利用逆補(bǔ)償?shù)乃枷虢⑷缦慢X隙逆補(bǔ)函數(shù)(inverse backlash function): 其中: 考慮到在實(shí)際系統(tǒng)中,參數(shù)KB、Br以及Bl是難以進(jìn)行準(zhǔn)確測(cè)量的, 因此實(shí)際的逆輸入uI可以設(shè)計(jì)為 另一種需要考慮的非線性是執(zhí)行機(jī)構(gòu)的延遲特性, 此處僅作簡(jiǎn)要的說(shuō)明.由于機(jī)載計(jì)算機(jī)有限的處理速度和執(zhí)行機(jī)構(gòu)的動(dòng)態(tài)特性, 從采集導(dǎo)航數(shù)據(jù)、機(jī)載計(jì)算機(jī)計(jì)算并發(fā)出控制指令到作動(dòng)器實(shí)際的控制效果, 必然會(huì)有一定的延遲, 如圖6所示.雖然這些延遲在普通低速飛行器的控制器設(shè)計(jì)中是可以忽略不計(jì)的, 但是對(duì)于至少以5Ma巡航的高超聲速飛行器來(lái)說(shuō), 0.1 s的執(zhí)行機(jī)構(gòu)延遲就可能產(chǎn)生近200 m的位置測(cè)量誤差, 這對(duì)于高性能的飛行控制是不被允許的. 圖6 高超聲速飛行控制中的延遲特性 另外, 由于延遲特性會(huì)引起的控制指令與實(shí)際控制輸出之間傳遞函數(shù)的相位移動(dòng), 進(jìn)而導(dǎo)致控制指令的失效.例如, 由于燃料泵的延遲特性, 超燃沖壓發(fā)動(dòng)機(jī)的燃流量指令Φc與實(shí)際燃流量Φ之間的傳遞函數(shù)可以表示為 式中:ξ=0.7,ω=20 rad/s, 延遲特性常數(shù)假設(shè)為τ=0.2 s.如果利用上述環(huán)節(jié)來(lái)響應(yīng)正弦燃流量指令:Φc=0.5 sin(πt)+0.5, 其輸出結(jié)果如圖7所示.可以看出, 具有延遲特性的環(huán)節(jié), 實(shí)際的燃流量與燃流量指令有著較大的誤差, 并且這一誤差將會(huì)隨著燃流量指令頻率的增加而進(jìn)一步增大.為了克服延遲效應(yīng), 可以利用時(shí)滯系統(tǒng)控制理論進(jìn)行高超聲速飛行器控制器的設(shè)計(jì), 另外, 所設(shè)計(jì)的控制律形式要盡量精簡(jiǎn), 以減少機(jī)載計(jì)算機(jī)在處理數(shù)據(jù)的耗時(shí).例如, 文獻(xiàn)[59]已經(jīng)證明: 采用文獻(xiàn)[33]中經(jīng)典的自適應(yīng)反向遞推設(shè)計(jì)方法可以實(shí)現(xiàn)一類帶有輸入時(shí)滯特性的線性系統(tǒng)的輸出跟蹤, 且不受最小相位條件的約束, 因此, 針對(duì)于吸氣式高超聲速飛行器執(zhí)行機(jī)構(gòu)的延遲問題, 可以利用其線性化模型設(shè)計(jì)飛行控制器. 圖7 延遲特性對(duì)于燃流量指令響應(yīng)的影響 Fig.7 Effects of delay on the response of fuel equivalency ratio command 3.2 容錯(cuò)控制 控制系統(tǒng)的故障可分為3種情形: 執(zhí)行機(jī)構(gòu)故障、傳感器故障以及組件故障[60].吸氣式高超聲速飛行器的氣動(dòng)舵面工作在高溫、高動(dòng)壓的惡劣環(huán)境下, 很可能出現(xiàn)執(zhí)行機(jī)構(gòu)部分失效甚至全部失效的情形, 因此, 所設(shè)計(jì)的控制器還需要具備一定的容錯(cuò)控制能力[61].一般來(lái)說(shuō), 容錯(cuò)控制主要分為兩類: 1)利用設(shè)計(jì)控制器的魯棒性來(lái)克服執(zhí)行機(jī)構(gòu)失效;2)通過(guò)引入故障的檢測(cè)機(jī)制來(lái)確定故障發(fā)生的位置和程度, 進(jìn)而采用一定的處理機(jī)制進(jìn)行克服. 對(duì)于吸氣式高超聲速飛行器容錯(cuò)控制的研究主要集中于第1類, 即: 通過(guò)設(shè)計(jì)具有強(qiáng)魯棒性或者自適應(yīng)能力的控制器來(lái)保證在執(zhí)行機(jī)構(gòu)、傳感器等出現(xiàn)故障時(shí)仍能達(dá)到一定的性能指標(biāo).例如: 文獻(xiàn)[62]利用動(dòng)態(tài)面反步法對(duì)于一類帶有舵面冗余的高超聲速飛行器設(shè)計(jì)了容錯(cuò)控制器, 實(shí)現(xiàn)了在部分舵面卡死情況下的指令跟蹤控制;文獻(xiàn)[63]利用擾動(dòng)觀測(cè)器增強(qiáng)型的反步法為高超聲速飛行器設(shè)計(jì)了跟蹤控制器, 并通過(guò)引入指令濾波器和輔助系統(tǒng)實(shí)現(xiàn)了飛行控制系統(tǒng)對(duì)于執(zhí)行機(jī)構(gòu)幅值、速度約束的魯棒性;文獻(xiàn)[64]通過(guò)在標(biāo)準(zhǔn)的動(dòng)態(tài)逆控制器中引入故障觀測(cè)器, 使得飛行控制系統(tǒng)能夠適應(yīng)一類突變的故障, 而對(duì)于其他類型的故障, 則利用支持向量機(jī)進(jìn)行在線補(bǔ)償;文獻(xiàn)[42]利用T-S模糊控制的方法考慮了執(zhí)行機(jī)構(gòu)部分失效的情形, 并保證了閉環(huán)系統(tǒng)的漸近穩(wěn)定性;文獻(xiàn)[65-66]設(shè)計(jì)了自適應(yīng)容錯(cuò)控制器, 使得在執(zhí)行機(jī)構(gòu)部分失效的情況下仍能實(shí)現(xiàn)有限時(shí)間的輸出跟蹤;文獻(xiàn)[67]利用反饋線性化模型設(shè)計(jì)了自適應(yīng)控制器, 在升降舵卡死的情況下保證系統(tǒng)的穩(wěn)定性, 并利用高增益觀測(cè)器實(shí)現(xiàn)了輸出反饋控制;文獻(xiàn)[68]利用神經(jīng)網(wǎng)絡(luò)估計(jì)執(zhí)行機(jī)構(gòu)故障對(duì)系統(tǒng)產(chǎn)生的影響, 進(jìn)而利用帶有指令預(yù)處理機(jī)制的反向遞推法設(shè)計(jì)了控制器;對(duì)于傳感器出現(xiàn)故障也有相關(guān)的研究[42, 69], 其中, 文獻(xiàn)[42]基于T-S模糊模型考慮了如下傳感器故障: 式中fsih、fsil分別為測(cè)量值的上界和下界.顯然, 如果fsil=fsih=0, 則代表測(cè)量信號(hào)完全丟失;如果fsil=fsih=1, 則代表傳感器沒有故障.基于此, 文獻(xiàn)[42]利用并行分布補(bǔ)償原理及線性矩陣不等式工具設(shè)計(jì)了模糊線性反饋控制器, 并實(shí)現(xiàn)了輸出的跟蹤.此外, 還有許多相關(guān)的研究成果限于篇幅無(wú)法詳細(xì)列舉說(shuō)明. 3.3 多目標(biāo)控制 大多數(shù)已有控制器設(shè)計(jì)的目標(biāo)為: 實(shí)現(xiàn)高超聲速飛行器輸出(速度、高度)的漸進(jìn)跟蹤以及系統(tǒng)狀態(tài)的收斂或有界.近期, 一些研究成果利用終端滑模變結(jié)構(gòu)控制技術(shù)(terminal sliding mode control, TSMC)實(shí)現(xiàn)了有限時(shí)間精確跟蹤, 即: 跟蹤誤差可以在特定有限的時(shí)間內(nèi)收斂到零, 并保持對(duì)于外界擾動(dòng)的魯棒性.然而, 僅僅實(shí)現(xiàn)對(duì)于輸出的跟蹤是遠(yuǎn)遠(yuǎn)不夠的, 還需要針對(duì)于多個(gè)性能指標(biāo)進(jìn)行控制系統(tǒng)的綜合設(shè)計(jì). 另外, 對(duì)于吸氣式高超聲速飛行器來(lái)說(shuō), 某些約束必須嚴(yán)格地進(jìn)行限制, 這主要體現(xiàn)在超燃沖壓發(fā)動(dòng)機(jī)的工作條件.一般來(lái)說(shuō), 為了滿足發(fā)動(dòng)機(jī)的進(jìn)氣條件,飛行攻角α和側(cè)滑角β的上界近似與飛行馬赫數(shù)有以下關(guān)系[72](如圖8所示): 式中:Kα>0,Bα>0,Kβ>0,Bβ>0為特定常數(shù), 并且4Kα+Bα≈0, 4Kβ+Bβ≈0.由此可見, 隨著馬赫數(shù)的不斷降低, 攻角和側(cè)滑角的約束越來(lái)越嚴(yán)格(尤其在M∞=4附近), 這對(duì)于吸氣式高超聲速飛行器的減速機(jī)動(dòng)控制具有極大的挑戰(zhàn)性.與此同時(shí), 由于高超聲速飛行會(huì)產(chǎn)生嚴(yán)重的氣動(dòng)熱, 因此對(duì)于飛行器本身的熱防護(hù)措施是及其苛刻的.從另一角度來(lái)說(shuō), 如果設(shè)計(jì)的控制器能夠充分地考慮相關(guān)方面的約束, 如合理的熱流量、動(dòng)壓變化范圍等, 則會(huì)在很大程度上減輕熱防護(hù)系統(tǒng)的設(shè)計(jì)壓力, 這就需要在飛行過(guò)程中嚴(yán)格地限制氣動(dòng)舵的偏轉(zhuǎn)角為 圖8 攻角、側(cè)滑角以及氣動(dòng)舵偏轉(zhuǎn)角的約束 Fig.8 Constraints on angle of attack, angle of sideslip and deflection angles of aerodynamic control surfaces 其中Ωhard為硬指標(biāo)確定的可行域. 一般來(lái)說(shuō), 對(duì)于該類問題的求解是十分困難的.近期, 文獻(xiàn)[73]通過(guò)引入控制Barrier函數(shù)(control barrier function, CBF)的概念, 利用二次規(guī)劃解決了一類多目標(biāo)控制問題.但是在吸氣式高超聲速飛行器控制領(lǐng)域還沒有相關(guān)方面的研究, 是一個(gè)具有實(shí)際意義的研究方向. 3.4 切換控制 吸氣式高超聲速飛行器還涉及相關(guān)的模式切換, 主要包括: 飛行模式的切換、動(dòng)力系統(tǒng)的切換以及執(zhí)行機(jī)構(gòu)的切換, 如圖9所示.目前對(duì)于吸氣式高超聲速飛行器控制的研究主要集中在巡航段, 但實(shí)際的飛行任務(wù)或者機(jī)動(dòng)過(guò)程必然要經(jīng)歷上升段和下降段.由于飛行器在各個(gè)飛行階段的動(dòng)態(tài)特性是不盡相同的, 僅依靠單一的控制律很難統(tǒng)一地實(shí)現(xiàn)每個(gè)飛行段的控制指標(biāo), 因此, 往往需要設(shè)計(jì)不同的控制器參數(shù)、結(jié)構(gòu)來(lái)適應(yīng)不同的飛行階段.另一方面, 超燃沖壓發(fā)動(dòng)機(jī)在低馬赫數(shù)(一般M∞<4)是難以啟動(dòng)的, 一般需要與其他動(dòng)力裝置進(jìn)行組合以實(shí)現(xiàn)全包線的飛行.例如:X-43A的飛行實(shí)驗(yàn)就采用飛馬座火箭將其助推到特定的速度、高度, 進(jìn)而點(diǎn)燃超燃沖壓發(fā)動(dòng)機(jī)以維持高超聲速飛行, 對(duì)于X-43A與助推器分離的穩(wěn)定性問題,NASA的研究人員[74]做了大量的分析和驗(yàn)證.另外, 在某些大機(jī)動(dòng)飛行過(guò)程中, 需要執(zhí)行機(jī)構(gòu)提供充足的控制力、力矩.但由于氣動(dòng)舵(主要考慮升降舵)需要克服推力產(chǎn)生的抬頭力矩, 并且過(guò)大的舵偏角在高超聲速飛行中會(huì)產(chǎn)生嚴(yán)重氣動(dòng)熱和附加阻力, 因此其控制裕度是十分有限的.基于上述原因, 吸氣式高超聲速飛行器通常采用氣動(dòng)舵面與反作用力控制系統(tǒng)(reactioncontrolsystem,RCS)組合的方式來(lái)提供足夠的機(jī)動(dòng)能力, 即: 執(zhí)行機(jī)構(gòu)可能發(fā)生切換. 圖9 高超聲速飛行中的控制器切換問題 由此可見, 對(duì)于大機(jī)動(dòng)、大飛行包線的高超聲速飛行來(lái)說(shuō), 單一的控制參數(shù)、控制結(jié)構(gòu)往往難以滿足預(yù)定的控制指標(biāo).因此, 需要針對(duì)不同的情形設(shè)計(jì)切換控制系統(tǒng), 并能夠?qū)τ陂]環(huán)系統(tǒng)的穩(wěn)定性及性能進(jìn)行充分地分析, 而這也是目前吸氣式高超聲速飛行器控制的一個(gè)重要的研究方向.采用近似線性化的方法, 設(shè)計(jì)者可以將具有參數(shù)或結(jié)構(gòu)變化的吸氣式高超聲速飛行器控制問題表述成一類多模型切換控制問題: 3.5 制導(dǎo)與控制的一體化設(shè)計(jì) 眾所周知, 飛行器的制導(dǎo)與控制是緊密相連的.由于飛行系統(tǒng)的復(fù)雜性, 制導(dǎo)子系統(tǒng)與控制子系統(tǒng)的設(shè)計(jì)往往是分開進(jìn)行的.雖然這種模塊化設(shè)計(jì)思想在工程實(shí)際中證明是有效的, 但并不是最優(yōu)的設(shè)計(jì)方案: 1) 為了簡(jiǎn)化設(shè)計(jì)過(guò)程, 控制(制導(dǎo))模塊的設(shè)計(jì)忽略了其與制導(dǎo)(控制)模塊之間的弱耦合, 因此, 整合后的制導(dǎo)/控制系統(tǒng)往往會(huì)出現(xiàn)不匹配的情形, 需要進(jìn)行大量繁瑣的驗(yàn)證、修正工作;2) 制導(dǎo)/控制系統(tǒng)的模塊化設(shè)計(jì)往往具有一定的保守性, 并且在理論上難以保證閉環(huán)系統(tǒng)的穩(wěn)定性.這就促使設(shè)計(jì)者進(jìn)行制導(dǎo)/控制系統(tǒng)的一體化設(shè)計(jì), 即: 在整體上把握制導(dǎo)、控制之間的耦合、約束, 同時(shí)完成制導(dǎo)律與控制律的全部設(shè)計(jì)指標(biāo). 雖然制導(dǎo)/控制一體化的設(shè)計(jì)思想在20世紀(jì)80年代就已出現(xiàn)[77], 但由于各個(gè)通道之間的嚴(yán)重耦合(如飛行器的縱向運(yùn)動(dòng)與橫向運(yùn)動(dòng)), 目前大部分的研究成果僅僅局限于單通道的制導(dǎo)/控制一體化設(shè)計(jì).許多控制方法已成功應(yīng)用到一體化設(shè)計(jì), 例如: 最優(yōu)控制方法[77]、反向遞推控制方法[78]、滑模變結(jié)構(gòu)控制方法[79]、H控制方法[80]等.但這些研究成果對(duì)于以快速機(jī)動(dòng)為目標(biāo)的高超聲速飛行器來(lái)說(shuō)是遠(yuǎn)遠(yuǎn)不夠的.由于高超聲速飛行器需要大幅度的橫向機(jī)動(dòng), 各個(gè)通道之間往往具有嚴(yán)重的耦合.在這種情況下, 單通道一體化設(shè)計(jì)方法難以保證整個(gè)飛行系統(tǒng)的穩(wěn)定性.此外, 無(wú)法利用一些有益的耦合項(xiàng)來(lái)進(jìn)一步提高系統(tǒng)的控制性能.目前, 已有一些研究成果對(duì)于多通道耦合的制導(dǎo)/控制一體化設(shè)計(jì)進(jìn)行了一些探索, 例如: 非線性次優(yōu)控制方法[81-82]、反饋線性化控制方法[83]、分塊反向遞推控制方法[84]等. 另一個(gè)制約制導(dǎo)/控制一體化設(shè)計(jì)的因素是飛行過(guò)程中的各種約束.如多目標(biāo)控制部分所述, 由于系統(tǒng)狀態(tài)、執(zhí)行機(jī)構(gòu)存在特定的約束, 內(nèi)環(huán)控制系統(tǒng)往往無(wú)法精確跟蹤外環(huán)制導(dǎo)系統(tǒng)產(chǎn)生的控制指令, 進(jìn)而產(chǎn)生執(zhí)行機(jī)構(gòu)的飽和(氣動(dòng)舵)或者失效(超燃沖壓發(fā)動(dòng)機(jī)), 嚴(yán)重地危害了系統(tǒng)的穩(wěn)定性.帶有約束的制導(dǎo)/控制一體化設(shè)計(jì)方面的研究目前還是比較少的, 而對(duì)于吸氣式高超聲速飛行器來(lái)說(shuō)是一個(gè)具有實(shí)際意義的研究課題. 本文總結(jié)了吸氣式高超聲速飛行器控制系統(tǒng)設(shè)計(jì)中亟待解決的幾個(gè)問題.實(shí)際高超聲速飛行控制系統(tǒng)設(shè)計(jì)所面臨的問題遠(yuǎn)不止這些, 例如: 吸氣式高超聲速飛行器的細(xì)長(zhǎng)外形、薄壁結(jié)構(gòu)以及輕質(zhì)復(fù)合材料使其具有比普通飛行器更為明顯的彈性模態(tài), 但限于篇幅和作者的能力很難全部涉獵.值得說(shuō)明的是, 雖然飛行控制僅僅是整個(gè)高超聲速飛行器工程中的一個(gè)子系統(tǒng), 但卻是至關(guān)重要的.這是因?yàn)榭刂葡到y(tǒng)的設(shè)計(jì)還需要慎重考慮其與導(dǎo)航、制導(dǎo)子系統(tǒng)之間的融合, 并能充分滿足其他分系統(tǒng)(如飛行器結(jié)構(gòu)、推進(jìn)系統(tǒng)、熱防護(hù)系統(tǒng))的需求[2], 如圖10所示.可見, 吸氣式高超聲速飛行器控制系統(tǒng)的設(shè)計(jì)是一個(gè)涉及多學(xué)科的綜合問題, 仍有許多問題需要進(jìn)一步解決. 圖10 控制系統(tǒng)與各系統(tǒng)之間的關(guān)系 Fig.10 Relationship between the control subsystem and other subsystems 由于吸氣式高超聲速飛行器獨(dú)特、復(fù)雜的飛行動(dòng)態(tài)特性, 對(duì)其設(shè)計(jì)具有魯棒性、可靠性、高性能的控制器是非常具有挑戰(zhàn)性的.本文著重闡述了吸氣式高超聲速飛行器控制系統(tǒng)的設(shè)計(jì)方法: 模型線性化方法、反向遞推法、T-S模糊控制方法、自適應(yīng)和滑模變結(jié)構(gòu)控制方法, 進(jìn)而總結(jié)了實(shí)際控制器設(shè)計(jì)過(guò)程中需要克服的若干問題.限于文章篇幅和作者能力, 所提及的研究方法和控制問題是十分有限的.但有一點(diǎn)可以肯定, 對(duì)于吸氣式高超聲速飛行器控制系統(tǒng)的設(shè)計(jì)需要兼顧各個(gè)子系統(tǒng), 這樣所設(shè)計(jì)的控制器才具有實(shí)際的應(yīng)用價(jià)值, 同時(shí)也是今后高超聲速飛行器控制領(lǐng)域的努力方向. [1] WEEKS D, WALKER S, SACKHEIM R. Small satellites and the DARPA/Air Force FALCON program[J]. Acta Astronautica, 2005, 57(2-8): 469-477. DOI:10.1016/j.actaastro.2005.03.058. [2] 李惠峰. 高超聲速飛行器制導(dǎo)與控制技術(shù)[M]. 北京: 中國(guó)宇航出版社, 2012. [3] RODRIGUEZ A, DICKESON J, CIFDALOZ O, et al. Modeling and control of scramjet-powered hypersonic vehicles: challenges, trends, and tradeoffs[C]// AIAA Guidance, Navigation and Control Conference and Exhibit. Honolulu: AIAA, 2008. [4] VOLAND R, HUEBNER L, MCCLINTON C. X-43A hypersonic vehicle technology development[J]. Acta Astronautica, 2006, 59(1-5):181-191. DOI: 10.1016/j.actaastro.2006.02.021. [5] HANK J M, MURPHY J S, MUTZMAN R C. The X-51A scramjet engine flight demonstration program[C]// Proceedings of the 15thAIAA International Space Planes and Hypersonic Systems and Technologies Conference. Dayton: AIAA, 2008. [6] 崔爾杰. 近空間飛行器研究發(fā)展現(xiàn)狀及關(guān)鍵技術(shù)問題[J].力學(xué)進(jìn)展, 2009, 39(6): 658-673. CUI Erjie. Research statutes, development trends and key technical problems of near space flying vehicles[J]. Advances in Mechanics, 2009, 39(6): 658-673. [7] 孫長(zhǎng)銀, 穆朝絮, 余瑤. 近空間高超聲速飛行器控制的幾個(gè)科學(xué)問題研究[J]. 自動(dòng)化學(xué)報(bào), 2013, 39(11): 1901-1913. SUN Changyin, MU Chaoxu, YU Yao. Some control problems for near space hypersonic vehicles[J]. ACTA Automatica Sinica, 2013, 39(11): 1901-1913. [8] 黃琳, 段志生, 楊劍影. 近空間高超聲速飛行器對(duì)控制科學(xué)的挑戰(zhàn)[J]. 控制理論與應(yīng)用, 2011, 28(10): 1496-1505. HUANG Lin, DUAN Zhisheng, YANG Jianying.Challenges of control science in near space hypersonic aircrafts[J]. Control Theory & Applications, 2011, 28(10): 1496-1505. [9] 黃長(zhǎng)強(qiáng), 國(guó)海峰, 丁達(dá)理. 高超聲速滑翔飛行器軌跡優(yōu)化與制導(dǎo)綜述[J]. 宇航學(xué)報(bào), 2014, 35(4): 369-379. DOI:10.3873/j.issn.1000-1328.2014.04.001. HUANG Changqiang, GUO Haifeng, DING Dali. A survey of trajectory optimization and guidance for hypersonic gliding vehicle[J]. Journal of Astronautics, 2014, 35(4): 369-379. DOI:10.3873/j.issn.1000-1328.2014.04.001. [10]葉友達(dá). 高超聲速空氣動(dòng)力學(xué)研究進(jìn)展與趨勢(shì)[J]. 科學(xué)通報(bào), 2015, 60(12): 1095-1103. DOI: 10.1360/N972014-01180. YE Youda. Advances and prospects in hypersonic aerodynamics[J]. Chinese Science Bulletin, 60(12): 1095-1103. DOI: 10.1360/N972014-01180. [11]吳宏鑫, 孟斌. 高超聲速飛行器控制研究綜述[J]. 力學(xué)進(jìn)展, 2009, 39(6): 756-765. DOI: 10.3321/j.issn:1000-0992.2009.06.013. WU Hongxin, MENG Bin. Review on the control of hypersonic flight vehicles[J]. Advances in Mechanics, 2009, 39(6): 756-765. DOI: 10.3321/j.issn:1000-0992.2009.06.013. [12]XU Bin, SHI Zhongke. An overview on flight dynamics and control approaches for hypersonic vehicles[J]. Science China Information Sciences, 2015, 58(7): 1-19. DOI: 10.1007/s11432-014-5273-7. [13]王文博, 范國(guó)超, 許承東. 臨近空間高超聲速飛行器制導(dǎo)與控制技術(shù)研究綜述[J]. 戰(zhàn)術(shù)導(dǎo)彈技術(shù), 2013, (6): 32-36. DOI: 10.16358/j.issn.1009-1300.2015.06.06. WANG Wenbo,F(xiàn)AN Guochao,XU Chengdong. Survey of the guidance and control for near-space hypersonic vehicle[J]. Tactical Missile Technology, 2013, (6): 32-36. DOI: 10.16358/j.issn.1009-1300.2015.06.06. [14]王鵬, 金鑫, 張衛(wèi)民. FADS系統(tǒng)在尖楔前體高超聲速飛行器中的應(yīng)用[J]. 中國(guó)科學(xué):物理學(xué)力學(xué)天文, 2013, 43(9): 1105-1110. DOI: 10.1360/132012-314. WANG Peng, JIN Xin, ZHANG Weimin. Application of FADS system in hypersonic flight vehicles with sharp wedged fore-bodies[J]. SCIENTIA SINICA: Physica, Mechanica & Astronomica, 2013, 43(9): 1105-1110. DOI: 10.1360/132012-314. [15]華如豪, 葉正寅. 吸氣式高超聲速飛行器多學(xué)科動(dòng)力學(xué)建模[J]. 航空學(xué)報(bào), 2015, 36(1): 346-356. DOI:10.7527/S1000-6893.2014.0243. HUA Ruhao, YE Zhengyin. Multidisciplinary dynamics modeling and analysis of a generic hypersonic vehicle[J]. Acta Aeronautica ET Astronautica Sinica, 2015, 36(1): 346-356. DOI:10.7527/S1000-6893.2014.0243. [16]楊超, 許赟, 謝長(zhǎng)川. 高超聲速飛行器氣動(dòng)彈性力學(xué)研究綜述[J]. 航空學(xué)報(bào), 2010, 31(1): 1-11. YANG Chao, XU Yun, XIE Changchuan. Review of studies on aeroelasticity of hypersonic vehicles[J]. Acta Aeronautica ET Astronautica Sinica, 2010, 31(1): 1-11. [17]李惠峰, 肖進(jìn), 張冉. 高超聲速飛行器剛體/彈性體耦合動(dòng)力學(xué)建模[J]. 北京航空航天大學(xué)學(xué)報(bào), 2012, 38(2): 160-165. DOI: 11-2625 /V.20120221.1146.010. LI Huifeng, XIAO Jin, ZHANG Ran. Hypersonic vehicle rigid/elastic coupled dynamic modeling[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(2): 160-165. DOI: 11-2625/V.20120221.1146.010. [18]CHAVEZ F R, SCHMIDT D K. Analytical aeropropulsive/aeroelastic hypersonic-vehicle model with dynamic analysis[J]. Journal of Guidance, Control, and Dynamics, 1994, 17(6): 1308-1319.DOI: 10.2514/3.21349. [19]SHAUGHNESSY J, PINCKNEY S, MCMINN J, et al. Hypersonic vehicle simulation model: winged-coneconfiguration[R]. Langley: NASA Langley Research Center, 1990. [20]MARRISON C I, STENGEL R F. Design of robust control systems for a hypersonic aircraft[J]. Journal of Guidance, Control, and Dynamics, 1998, 21(1): 58-63. DOI: 10.2514/2.4197. [21]WANG Qian, STENGEL R F. Robust nonlinear control of a hypersonic aircraft[J]. Journal of Guidance, Control, and Dynamics, 2000, 23(4): 577-585.DOI: 10.2514/2.4580. [22]BOLENDER M A, DOMAN D B. Nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle[J]. Journal of Spacecraft and Rockets, 2007, 44(2): 374-387. DOI: 10.2514/1.23370. [23]PARKER J T, SERRANI A, YURKOVICH S, et al. Control-oriented modeling of an air-breathing hypersonic vehicle[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(3): 856-869. DOI: 10.2514/1.27830. [24]FIORENTINI L, SERRANI A, BOLENDER M A, et al. Nonlinear robust adaptive control of flexible airbreathing hypersonic vehicles[J]. Journal of Guidance, Control, and Dynamics, 2009, 32(2): 402-417. DOI: 10.2514/1.39210. [25]SIGTHORSSON D O, SERRANI A. Development of linear parameter-varying models of hypersonic airbreathing vehicles[C]//AIAA Guidance, Navigation, and Control Conference. Chicago: AIAA, 2009. DOI: 10.2514/6.2009-6282. [26]SHAKIBA M, SERRANI A. Control oriented modeling of 6-DOF hypersonic vehicle dynamics[C]//AIAA Guidance, Navigation, and Control Conference. Portland: AIAA, 2011. DOI:10.2514/6.2011-6227. [27]SERRANI A, BOLENDER M A. A nonlinear adaptive reconfigurable controller for a generic 6-DOF hypersonic vehicle model[C]//American Control Conference. Portland, OR: IEEE, 2014: 1384-1389. DOI: 10.1109/ACC.2014.6858885. [28]方洋旺, 柴棟, 毛東輝, 等. 吸氣式高超聲速飛行器制導(dǎo)與控制研究現(xiàn)狀及發(fā)展趨勢(shì)[J]. 航空學(xué)報(bào), 2014, 35(7): 1776-1786. DOI: 10.7527/S1000-6893.2014.0021. FANG Yangwang, CHAI Dong, MAO Donghui, et al. Status and development trend of the guidance and control for air-breathing hypersonic vehicle[J]. Acta Aeronautica ET Astronautica Sinica, 2014, 35(7): 1776-1786. DOI: 10.7527/S1000-6893.2014.0021. [29]曾開春, 向錦武. 高超聲速飛行器飛行動(dòng)力學(xué)特性不確定分析[J]. 航空學(xué)報(bào), 2013, 34(4): 798-808. DOI: 10.7527/S1000-6893.2013.0139. Zeng Kaichun, XIANG Jinwu. Uncertainty analysis of flight dynamic characteristics for hypersonic vehicles[J]. Acta Aeronautica ET Astronautica Sinica, 2013, 34(4): 798-808. DOI: 10.7527/S1000-6893.2013.0139. [30]REHMAN O, PETERSEN I, FIDAN B. Feedback linearization-based robust nonlinear control design for hypersonic flight vehicles[J]. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2012, 227(1): 3-11. DOI: 10.1177/0959651812447722. [31]REHMAN O, FIDAN B, PETERSEN I. Robust control system design for an uncertain nonlinear system using minmax LQG design method[J]. Asian Journal of Control, 2014, 16(4): 1029-1041. DOI: 10.1002/asjc.777. [32]GAO Gang, WANG Jinzhi. Observer-based fault-tolerant control for an air-breathing hypersonic vehicle model[J]. Nonlinear Dynamics, 2014, 76(1): 409-430. DOI: 10.1007/s11071-013-1135-x. [33]KRSTIC M, KANELLAKOPOULOS I, KOKOTOVIC P. Nonlinear and adaptive control design[M]. New York: Wiley, 1995. [34]FIORENTINI L, SERRANI A. Nonlinear adaptive control design for non-minimum phase hypersonic vehicle models with minimal control authority[C]// Proceedings of the 48th IEEE Conference on Decision and Control. Shanghai: IEEE, 2009: 1405-1410. DOI: 10.1109/CDC.2009.5400744 [35]SUN Haibin, LI Shihua, YANG Jun, et al. Non-linear disturbance observer-based back-stepping control for airbreathing hypersonic vehicles with mismatched disturbances[J]. IET Control Theory & Application, 2014, 8(17): 1852-1865. DOI: 10.1049/iet-cta.2013.0821. [36]ZONG Qun, WANG Fang, TIAN Bailing, et al. Robust adaptive dynamic surface control design for a flexible air-breathing hypersonic vehicle with input constraints and uncertainty[J]. Nonlinear Dynamics, 2014, 78(1): 289-315. DOI: 10.1007/s11071-014-1440-z. [37]XU Bin. Robust adaptive neural control of flexible hypersonic flight vehicle with dead-zone input nonlinearity[J]. Nonlinear Dynamics, 2015, 80(3): 1509-1520. DOI:10.1007/s11071-015-1958-8. [38]XU Bin, YANG Chenguang, PAN Yongping. Global neural dynamic surface tracking control of strict-feedback systems with application to hypersonic flight vehicle[J]. IEEE Transactions on Neural Networks and Learning Systems, 2015, 26(10): 2563-2575.DOI: 10.1109/TNNLS.2015.2456972. [39]XU Bin, WANG Shixing, GAO Daoxiang, et al. Command filter based robust nonlinear control of hypersonic aircraft with magnitude constraints on states and actuators[J]. Journal of Intelligent & Robotic Systems, 2014, 73(1): 233-247.DOI: 10.1007/s10846-013-9941-4. [40]FARRELL J, POLYCARPOU M, SHARMA M, et al. Command filtered backstepping[J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1391-1395.DOI: 10.1109/TAC.2009.2015562. [41]HU Xiaoxiang, WU Ligang, HU Changhua, et al. Fuzzy guaranteed cost tracking control for a flexible air-breathing hypersonic vehicle[J]. IET Control Theory & Application, 2012, 6(9): 1238-1249. DOI: 10.1049/iet-cta.2011.0065. [42]HU Xiaoxiang, GAO Huijun, KARIMI H R, et al. Fuzzy reliable tracking control for flexible air-breathing hypersonic vehicles[J]. International Journal of Fuzzy Systems, 2011, 13(4): 323-334. [43]HU Xiaoxiang, WU Ligang, HU Changhua, et al. Adaptive fuzzy integral sliding mode control for flexible air-breathing hypersonic vehicles subject to input nonlinearity[J]. Journal of Aerospace Engineering, 2013, 26(4): 721-734. DOI:10.1061/(ASCE)AS.1943-5525.0000193. [44]HU Xiaoxiang, WU Ligang, HU Changhua, et al. Dynamic output feedback control of a flexible air-breathing hypersonic vehicle via T-S fuzzy approach[J]. International Journal of Systems Science, 2014, 45(8): 1740-1756.DOI: 10.1080/00207721.2012.749547. [45]BROCANELLI M, GUNBATAR Y, SERRANI A, et al. Robust control for unstart recovery in hypersonic vehicles[C]//AIAA Guidance, Navigation, and Control Conference. Minneapolis: AIAA, 2012. DOI: 10.2514/6.2012-4698. [46]WIESE D P, ANNASWAMY A M, MUSE J A, et al. Adaptive control of a generic hypersonic vehicle[C]//AIAA Guidance, Navigation, and Control Conference. Boston: AIAA, 2013. DOI: 10.2514/6.2013-4514. [47]IOANNOU P, FIDAN B. Adaptive control tutorial[M]. Philadelphia: SIAM, 2006. [48]WU Ligang, SHI Peng, SU Xiaojie. Sliding mode control of uncertain parameter-switching hybrid systems[M]. London: Wiley, 2014. DOI: 10.1002/9781118862612. [49]WANG Na , YAO Xiuming, LI Wenshuo. Nonlinear disturbance observer-based sliding mode control for flexible airbreathing hypersonic vehicles[J]. Mathematical Problems in Engineering, 2015, 2015:1-15. DOI: 10.1155/2015/675659. [50]CHENG Xianlei, TANG Guojian, WANG Peng, et al. Predictive sliding mode control for attitude tracking of hypersonic vehicles using fuzzy disturbance observer[J]. Mathematical Problems in Engineering. DOI: 10.1155/2015/727162. [51]WANG Jianmin, WU Yunjie, DONG Xiaomeng. Recursive terminal sliding mode control for hypersonic flight vehicle with sliding mode disturbance observer[J]. Nonlinear Dynamics, 2015, 81(3): 1489-1510. DOI: 10.1007/s11071-015-2083-4. [52] SHAO Xingling, WANG Honglun. Sliding mode based trajectory linearization control for hypersonic reentry vehicle via extended disturbance observer[J]. ISA Transactions, 2014, 53(6): 1771-1786. DOI: 10.1016/j.isatra.2014.09.021. [53]WANG Jie, ZONG Qun, SU Rui, et al. Continuous high order sliding mode controller design for a flexible air-breathing hypersonic vehicle[J]. ISA Transactions, 2014, 53(3): 690-698. DOI:10.1016/j.isatra.2014.01.002. [54]WANG Peng, TANG Guojian, WU Jie. Sliding mode decoupling control of a generic hypersonic vehicle based on parametric commands[J]. Science China Information Sciences, 2015, 58(5): 1-14. DOI: 10.1007/s11432-014-5122-8. [55]CHEN Mou, WU Qinxian, JIANG Changsheng, et al. Guaranteed transient performance based control with input saturation for near space vehicles[J]. Science China Information Sciences, 2014, 57(5): 1-12. DOI: 10.1007/s11432-013-4883-9. [56]AN Hao, LIU Jianxing, WANG Changhong, et al. Disturbance observer-based antiwindup control for air-breathing hypersonic vehicles[J]. IEEE Transactions on Industrial Electronics, 2016, 63(5): 3038-3049.DOI: 10.1109/TIE.2016.2516498. [57]ZHOU Jing, WEN Changyun. Adaptive backstepping control of uncertain systems: nonsmooth nonlinearities[M]. Berlin Heidelberg: Springer-Verlag, 2008. DOI:10.1007/978-3-540-77807-3_2. [58]ZHOU Jing, WEN Changyun, ZHANG Ying. Adaptive backstepping control of a class of uncertain nonlinear systems with unknown backlash-like hysteresis[J]. IEEE Transactions on Automatic Control, 2004, 49(10): 1751-1759. DOI: 10.1109/TAC.2004.835398. [59]ZHOU Jing, WEN Changyun. Adaptive backstepping control of uncertain systems with unknown input time-delay[J]. Automatica, 2009, 45(6): 1415-1422. DOI: 10.1016/j.automatica.2009.01.012. [60]GAO Zhiwei, CECATI C, DING S X. A survey of fault diagnosis and fault-tolerant techniques-Part I: Fault diagnosis with model-based and signal-based approaches[J]. IEEE Transactions on Industrial Electronics, 2015, 62(6): 3757-3767. DOI: 10.1109/TIE.2015.2417501. [61]錢佳淞, 齊瑞云, 姜斌. 高超聲速飛行器再入容錯(cuò)制導(dǎo)技術(shù)綜述[J]. 飛行力學(xué), 2015, 33(5): 390-394. QIAN Jiasong, QI Ruiyun, JIANG Bin. Review of reentry fault-tolerant guidance technology on hypersonic vehicles[J]. Flight Dynamics, 2015, 33(5): 390-394. [62]黃宇海, 齊瑞云, 姜斌, 等. 基于動(dòng)態(tài)面backstepping控制的高超聲速飛行器自適應(yīng)故障補(bǔ)償設(shè)計(jì)[J]. 中國(guó)科學(xué)技術(shù)大學(xué)學(xué)報(bào), 2012, 42(9): 768-774. DOI: 10.3969/j.issn.0253-2778.2012.09.011. HUANG Yuhai, QI Ruiyun, JIANG Bin, et al. Adaptive failure compensation design for hypersonic vehicles based on dynamic surface backstepping control[J]. Journal of University of Science and Technology of China, 2012, 42(9): 768-774. DOI: 10.3969/j.issn.0253-2778.2012.09.011. [63]AN Hao, LIU Jianxing, WANG Changhong, et al. Approximate back-stepping fault-tolerant control of the flexible air-breathing hypersonic vehicles[J]. IEEE/ASME Transactions on Mechatronics, 2016, 21(3): 1680-1691. DOI: 10.1109/TMECH.2015.2507186. [64]CHEN Fuyang, WANG Zheng, TAO Gang, et al. Robust adaptive fault-tolerant control for hypersonic flight vehicles with multiple faults[J]. Journal of Aerospace Engineering, 2015, 28(4): 04014111. DOI: 10.1061/(ASCE)AS.1943-5525.0000449. [65]WANG Jie, ZONG Qun, HE Xiao, et al. Adaptive finite-time control for a flexible hypersonic vehicle with actuator fault[J]. Mathematical Problems in Engineering, 2013, 2013: 920796. DOI: 10.1155/2013/920796. [66]JI Yuehui, ZHOU Hailiang, ZONG Qun. Adaptive active fault-tolerant control of generic hypersonic flight vehicles[J]. Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering, 2015, 229(2): 130-138.DOI: 10.1177/0959651814552809. [67]HE Jingjing, QIN Ruiyun, JIANG Bin, et al. Adaptive output feedback fault-tolerant control design for hypersonic flight vehicles[J]. Journal of the Franklin Institute, 2015, 352(5): 1811-1835. DOI: 10.1016/j.jfranklin.2015.01.016. [68]FU Wenxing, WANG Yuji, ZHU Supeng, et al. Neural adaptive control of hypersonic aircraft with actuator fault using randomly assigned nodes[J]. Neurocomputing, 2016, 174(Part B, 22): 1070-1076. DOI: 10.1016/j.neucom.2015.10.023. [69]GAO Zhifeng, LIN Jinxing, CAO Teng. Robust fault tolerant tracking control design for a linearized hypersonic vehicle with sensor fault[J]. International Journal of Control, Automation and Systems, 2015, 13(3): 672-679.DOI:10.1007/s12555-014-0169-2. [70]BECHLIOULIS C P, ROVITHAKIS G A. Robust adaptive control of feedback linearizable MIMO nonlinear systems with prescribed performance[J]. IEEE Transactions on Automatic Control, 2008, 53(9): 2090-2099. DOI: 10.1109/TAC.2008.929402. [71]BECHLIOULIS C P, ROVITHAKIS G A. Adaptive control with guaranteed transient and steady state tracking error bounds for strict feedback systems[J]. IEEE Transactions on Automatic Control, 2009, 45(2): 532-538.DOI: 10.1016/j.automatica.2008.08.012. [72]BOLENDER M, WILKIN H, JACOBSEN L, et al. Flight dynamics of a hypersonic vehicle during inlet unstart[C]//Proceedings of the 16th AIAA/DLR/DGLR International Space Planes and Hypersonic Systems and Technologies Conference. Bremen: AIAA, 2009. DOI: 10.2514/6.2009-7292. [73]AMES A D, GRIZZLE J W, TABUADA P. Control barrier function based quadratic programs with application to adaptive cruise control[C]//Proceedings of the IEEE 53rd Annual Conference on Decision and Control. Los Angeles, CA: IEEE Compendex, 2014: 6271-6278. DOI: 10.1109/CDC.2014.7040372. [74]PEEBLES C. Road to Mach 10: lessons learned from the X-43A flight research program[M]. Reston: AIAA, 2008. [75]LIBERZON D. Switching in systems and control[M]. New York: Springer Science & Business Media, 2003. [76]SUN Z, GE S. Switched linear systems-control and design[M]. Berlin: Springer Science & Business Media, 2004. [77]WILLIAMS D, RICHMAN J, FRIEDLAND B. Design of an integrated strapdown guidance and control system for a tactical missile[C]. Guidance and Control Conference. Gatlinburg: AIAA, 1983. DOI:10.2514/6.1983-2169. [78]SHARMA M, RICHARDS N. Adaptive, integrated guidance and control for missile interceptors[C]. AIAA Guidance, Navigation, and Control Conference and Exhibit. Providence: AIAA, 2004. DOI: 10.2514/6.2004-4880. [79]SHIMA T, IDAN M, GOLAN O. Sliding mode control for integrated missile autopilot guidance[J]. Journal of Guidance, Control, and Dynamics, 2006, 29(2): 250-260. DOI:10.2514/1.14951. [80]GUO Jianguo, ZHOU Jun. Integrated guidance-control system design based onHcontrol[C]//Proceedings of the 2010 International Conference on Electrical and Control Engineering. Wuhan: IEEE, 2010: 1204-1207. DOI: 10.1109/iCECE.2010.300. [81]VADDI S S, MENON P K, OHLMEYER E J. Numerical SDRE approach for missile integrated guidance control[J]. Journal of Guidance, Control, and Dynamics, 2009, 32(2): 699-703.DOI: 10.2514/1.34291. [82]XIN Min, BALAKRISHNAN S N, OHLMEYER E J. Integrated guidance and control of missiles withθ-D method[J]. IEEE Transactions on Control Systems Technology, 2006, 14(6): 981-992. DOI: 10.1109/TCST.2006.876903. [83]尹永鑫, 楊明, 王子才. 導(dǎo)彈三維制導(dǎo)控制一體化設(shè)計(jì)[J]. 電機(jī)與控制學(xué)報(bào), 2010, 14(3): 87-91. DOI: 10.3969/j.issn.1007-449X.2010.03.016. YIN Yongxin, YANG Ming, WANG Zicai. Three-dimensional guidance and control for missile[J]. Electric Machines and Control, 2010, 14(3): 87-91. DOI: 10.3969/j.issn.1007-449X.2010.03.016. [84]KIM B, CALISE A, SATTIGERI R. Adaptive, integrated guidance and control design for line-of-sight based formation flight[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(5): 1386-1398.DOI: 10.2514/1.27758. (編輯 張 紅) Recent progress in control of air-breathing hypersonic vehicles WU Ligang, AN Hao, LIU Jianxing, WANG Changhong (School of Astronautics, Harbin Institute of Technology, Harbin 150001, China) With the rapid development of the scramjet, air-breathing hypersonic vehicles(AHVs) are receiving worldwide attentions, while the control system design is of the most importance. Firstly, the developments in modeling of AHVs are briefly reviewed to illustrate the complexity of the controller design. Secondly, we concentrate to display several types of design methods for AHVs, i.e., linearized model-based controller design, back-stepping controller design, T-S fuzzy controller design, adaptive control and sliding mode control. Finally, this paper summarizes several practical problems that should be taken into account at design level, for example, actuator nonlinearity, fault-tolerance control, multi-objective control, switching control, etc., which could also be regarded as some potential research directions in the control system design for AHVs. air-breathing hypersonic vehicles (AHVs); control-oriented model; control system design; practical problem; progress 10.11918/j.issn.0367-6234.2016.10.001 2016-04-14 國(guó)家自然科學(xué)基金(61525303) 吳立剛(1977—), 男, 教授, 博士生導(dǎo)師; 吳立剛, ligangwu@hit.edu.cn V11 A 0367-6234(2016)10-0001-16 王常虹(1961—), 男, 教授, 博士生導(dǎo)師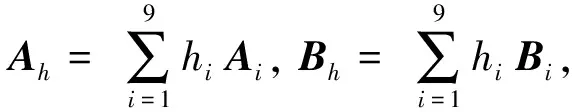
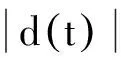
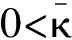
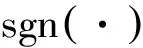
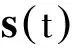
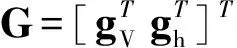
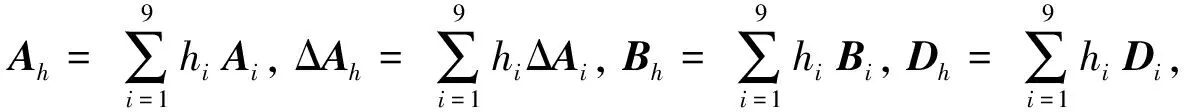
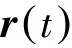
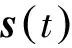
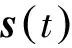
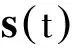
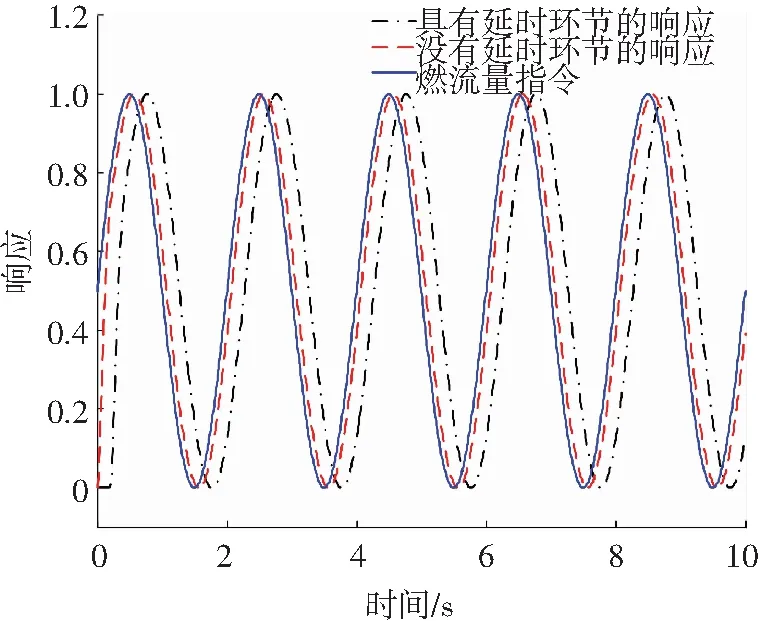
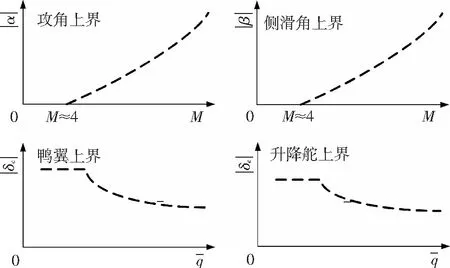
3 吸氣式高超聲速飛行器控制面臨的問題

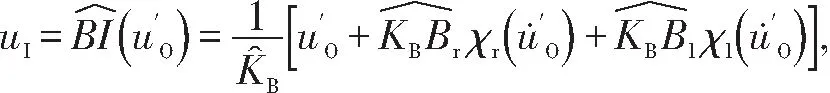
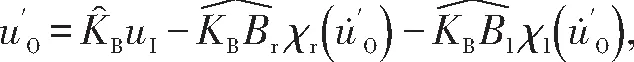

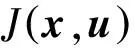
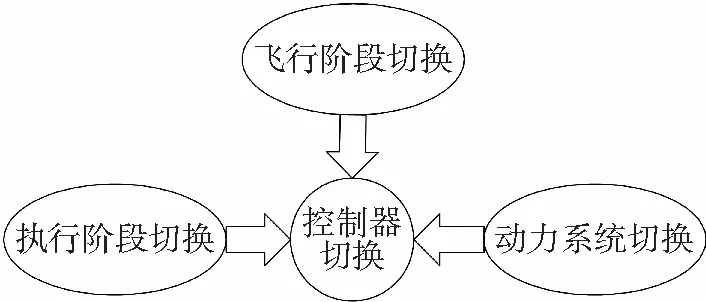


4 結(jié) 語(yǔ)

