飛輪系統(tǒng)的符號(hào)動(dòng)力學(xué)故障檢測(cè)方法

王日新，龔學(xué)兵，徐敏強(qiáng)，李玉慶

(哈爾濱工業(yè)大學(xué) 航天學(xué)院，哈爾濱 150001)

?

飛輪系統(tǒng)的符號(hào)動(dòng)力學(xué)故障檢測(cè)方法

王日新，龔學(xué)兵，徐敏強(qiáng)，李玉慶

(哈爾濱工業(yè)大學(xué) 航天學(xué)院，哈爾濱 150001)

為檢測(cè)飛輪系統(tǒng)的微弱故障, 提出一種基于符號(hào)動(dòng)力學(xué)的故障檢測(cè)方法.首先，利用符號(hào)動(dòng)力學(xué)算法將飛輪的電流數(shù)據(jù)進(jìn)行字符映射，實(shí)現(xiàn)信號(hào)降噪、數(shù)據(jù)壓縮.其次，利用D階馬爾科夫過(guò)程定義電流字符序列的變異過(guò)程，且根據(jù)字符序列的熵值變化率確立算法的字符個(gè)數(shù)，并計(jì)算字符的概率狀態(tài)轉(zhuǎn)移矩陣.最后，根據(jù)概率狀態(tài)轉(zhuǎn)移矩陣求解字符概率特征向量，并利用特征向量之間的距離閾值檢測(cè)飛輪的故障.仿真結(jié)果表明:該方法能夠根據(jù)字符概率特征向量之間的距離區(qū)分不同嚴(yán)重程度的飛輪系統(tǒng)故障，實(shí)現(xiàn)微弱故障的檢測(cè);與擴(kuò)展卡爾曼濾波算法相比，該方法不需復(fù)雜的動(dòng)力學(xué)建模，且僅利用單變量即可實(shí)現(xiàn)飛輪的故障檢測(cè).此外，利用過(guò)程數(shù)據(jù)，該方法可以快速學(xué)習(xí)衛(wèi)星其他部件的行為，并檢測(cè)故障。

符號(hào)動(dòng)力學(xué)；飛輪；有限狀態(tài)時(shí)序機(jī)；故障檢測(cè)；擴(kuò)展卡爾曼濾波

隨著納米衛(wèi)星、小衛(wèi)星的應(yīng)用與推廣，衛(wèi)星系統(tǒng)的測(cè)點(diǎn)設(shè)置受到體積的限制，衛(wèi)星系統(tǒng)的故障檢測(cè)、診斷只能利用較少的觀測(cè)變量.廣泛使用的閉環(huán)控制使得航天器的早期故障難以被檢測(cè)[1].航天器長(zhǎng)期在失重、高低溫交變等惡劣的環(huán)境中運(yùn)行，早期故障容易惡化，最終導(dǎo)致系統(tǒng)部件失效，進(jìn)而產(chǎn)生災(zāi)難性的后果[2]，因此，早期故障檢測(cè)能夠幫助衛(wèi)星提早隔離故障部件，合理規(guī)劃衛(wèi)星任務(wù)，降低運(yùn)行成本.

針對(duì)飛輪的故障檢測(cè)問(wèn)題，目前研究主要集中在各種觀測(cè)器的設(shè)計(jì).利用觀測(cè)器能精確的識(shí)別、檢測(cè)飛輪的故障參數(shù)，但數(shù)學(xué)公式的推導(dǎo)、證明非常復(fù)雜.例如：基于迭代學(xué)習(xí)型的觀測(cè)器[3]能通過(guò)自主迭代學(xué)習(xí)算法精確的估計(jì)飛輪的故障.正交匹配追蹤算法[4](OPM)能夠用于追蹤飛輪系統(tǒng)的瞬時(shí)故障和緩變故障.自適應(yīng)的神經(jīng)元參數(shù)估計(jì)方法[5]能夠利用飛輪系統(tǒng)多個(gè)輸入、輸出量對(duì)非線性系統(tǒng)建模，并檢測(cè)、分離飛輪系統(tǒng)的故障.未知輸入觀測(cè)器[6]通過(guò)分析殘差向量的變化對(duì)飛輪的傳感器以及系統(tǒng)的故障參數(shù)進(jìn)行檢測(cè)、分離.基于擴(kuò)展卡爾曼濾波的動(dòng)量輪故障檢測(cè)方法[7]將動(dòng)量輪的物理模型參數(shù)擴(kuò)展為狀態(tài)空間的狀態(tài)量，實(shí)現(xiàn)飛輪物理參數(shù)的實(shí)時(shí)跟蹤與檢測(cè).基于自適應(yīng)觀測(cè)器與擴(kuò)張狀態(tài)觀測(cè)器的綜合觀測(cè)器[8]能在執(zhí)行器輸出量不可得的限制條件下實(shí)現(xiàn)故障檢測(cè)，并獲得飛輪的真實(shí)輸出估計(jì).自適應(yīng)的神經(jīng)模糊推理系統(tǒng)[9](ANFIS)能夠利用系統(tǒng)觀測(cè)變量的輸入、輸出與信號(hào)指令等數(shù)據(jù)來(lái)估計(jì)飛輪的物理參數(shù)，從而檢測(cè)飛輪系統(tǒng)的故障.算法的收斂性是上述模型設(shè)計(jì)的關(guān)鍵問(wèn)題，建模精度會(huì)影響算法的收斂性.對(duì)無(wú)法精確建模的物理系統(tǒng)，基于數(shù)據(jù)分析[10]的故障檢測(cè)方法能避免物理建模，根據(jù)觀測(cè)數(shù)據(jù)，利用概率推理實(shí)現(xiàn)航天器的故障檢測(cè)、診斷.

針對(duì)物理建模或者參數(shù)獲取存在困難的復(fù)雜系統(tǒng)，本文從觀測(cè)數(shù)據(jù)出發(fā)，進(jìn)行故障檢測(cè)，避免物理建模；上述的故障檢測(cè)方法要求多個(gè)觀測(cè)變量，而本文只需要一個(gè)觀測(cè)變量.利用所有變量進(jìn)行故障檢測(cè)將增加航天器系統(tǒng)的操作與維護(hù)成本.基于符號(hào)動(dòng)力學(xué)[11-13]的模型能夠簡(jiǎn)單、快速的提取系統(tǒng)的非線性特征，因此，基于符號(hào)動(dòng)力學(xué)的單變量故障檢測(cè)方法能簡(jiǎn)單、快速的提取飛輪的非線性特征，而字符映射使得該方法能夠快速處理大量的觀測(cè)數(shù)據(jù)，適合衛(wèi)星實(shí)時(shí)在線故障檢測(cè).且字符映射能夠降低系統(tǒng)噪聲的影響，使得本文算法能夠更加容易檢測(cè)飛輪的微弱故障.基于上述原因，本文建立飛輪系統(tǒng)的Simulink仿真模型，設(shè)置兩種故障并采集相應(yīng)的電流信號(hào)，利用符號(hào)動(dòng)力學(xué)模型構(gòu)建電流信號(hào)的狀態(tài)轉(zhuǎn)移矩陣，并計(jì)算健康狀態(tài)的字符概率距離，通過(guò)設(shè)定的閾值檢測(cè)飛輪系統(tǒng)的故障.

1 飛輪模型

常見(jiàn)的飛輪系統(tǒng)故障類(lèi)型[14]主要有：軸承卡死、軸承性能異常、電機(jī)不轉(zhuǎn)、電機(jī)性能下降、殼體與輪體組件異常等幾類(lèi)故障模式.按照故障變化的快慢可以劃分為緩變故障與突變故障.而早期故障一般都是一類(lèi)緩變故障，隨著時(shí)間推移慢慢影響飛輪的性能，本文為了模擬早期故障，調(diào)整故障參數(shù)，產(chǎn)生一組不同故障幅值的故障數(shù)據(jù).主要有電機(jī)增益變小故障與摩擦力力矩增大故障.

1.1 飛輪模型

根據(jù)文獻(xiàn)[15]給出的ITHACO-A型飛輪的數(shù)學(xué)模型，建立基于Simulink的飛輪高精度開(kāi)環(huán)系統(tǒng)仿真模型，如圖1所示.

圖1中的相關(guān)參數(shù)介紹如下：Vtc為等效的直流電動(dòng)機(jī)驅(qū)動(dòng)控制力矩，主要是電壓控制；Gd為電機(jī)驅(qū)動(dòng)增益；ωd為驅(qū)動(dòng)帶寬；Im為電機(jī)電流；Kt為電機(jī)轉(zhuǎn)動(dòng)系數(shù)；Ke為電機(jī)電動(dòng)勢(shì)反饋系數(shù)；Ibus為母線電流；Vbus為母線電壓；Rin為輸入電阻；Kf為電壓反饋增益；τv為滑動(dòng)摩擦力矩；τC為靜摩擦力矩，也叫庫(kù)倫摩擦力矩；τz為控制力矩；J為飛輪轉(zhuǎn)動(dòng)慣量；θα為力矩噪聲引起的角誤差；ωα為高通噪聲濾波器頻率；ωs為轉(zhuǎn)速限制閾值；Ks為轉(zhuǎn)速限制增益系數(shù)；ω為飛輪的實(shí)時(shí)轉(zhuǎn)速.

圖1 飛輪高精度開(kāi)環(huán)系統(tǒng)仿真模型

1.2 動(dòng)量輪開(kāi)環(huán)系統(tǒng)的數(shù)學(xué)模型

根據(jù)圖1的仿真模塊，建立飛輪開(kāi)環(huán)系統(tǒng)的狀態(tài)空間模型為

(1)

(2)

式中：ψ1(Im,ω)、ψ2(ω)、ψ3(ω)分別描述了電動(dòng)勢(shì)力矩限制、軸承摩擦力與力矩干擾、電機(jī)轉(zhuǎn)速限制這3個(gè)非線性模塊.飛輪仿真模型的參數(shù)設(shè)置見(jiàn)表1.

表1 飛輪參數(shù)

式(1),(2)反映了飛輪在姿態(tài)控制過(guò)程中，電流與系統(tǒng)狀態(tài)的關(guān)系密切，系統(tǒng)的閉環(huán)控制必然引起電流的變化，通過(guò)分析電流的變化規(guī)律能夠發(fā)現(xiàn)系統(tǒng)的早期故障特征.因此，本文主要分析的信號(hào)是飛輪的電流信號(hào).

2 非線性系統(tǒng)的特征提取

針對(duì)非線性系統(tǒng)，其動(dòng)態(tài)特征提取主要通過(guò)相平面分析、小擾動(dòng)線性化、仿真分析等方法完成，主要從非線性方程中提取動(dòng)態(tài)系統(tǒng)的固有模式.例如：平衡點(diǎn)的個(gè)數(shù)、自持振蕩現(xiàn)象.而從非線性系統(tǒng)的觀測(cè)數(shù)據(jù)進(jìn)行非線性分析，主要通過(guò)信號(hào)處理的方法完成特征提取.利用信號(hào)處理的技術(shù)提取非線性系統(tǒng)的固有模式.一般可分為：

1)信號(hào)預(yù)處理.主要是對(duì)樣本數(shù)據(jù)進(jìn)行降噪，利用時(shí)域、頻域或者時(shí)頻域的分析方法對(duì)數(shù)據(jù)進(jìn)行降噪處理.

2)相空間重構(gòu)技術(shù). 基于采樣定理，利用時(shí)間延遲變量來(lái)重構(gòu)狀態(tài)向量為

式中: T為時(shí)間延遲變量，dE為相空間的維度.

3)信號(hào)分類(lèi). 信號(hào)分類(lèi)與識(shí)別主要依據(jù)系統(tǒng)的不變量.這類(lèi)不變量具有吸引子的性質(zhì)，這類(lèi)不變量并不局限于某一特殊的相軌跡.在非線性問(wèn)題中主要有兩類(lèi)不變量：分形維數(shù)與李雅普洛夫指數(shù).

4)建模與預(yù)測(cè). 主要是確定動(dòng)態(tài)模型的參數(shù)，判斷參數(shù)是否與不變量(李雅普洛夫指數(shù)與分形維數(shù))一致.

上述3個(gè)步驟主要是分析隨機(jī)系統(tǒng)，并提取隨機(jī)系統(tǒng)的自由度或者復(fù)雜度，從而用最簡(jiǎn)單的結(jié)構(gòu)去表示隨機(jī)系統(tǒng)的基本特征或者固有模式.最后步驟是利用基本特征定義系統(tǒng)行為，并用于判斷系統(tǒng)的異常狀態(tài)或者早期故障.

在非線性系統(tǒng)中，慢變參數(shù)能緩慢的改變非線性系統(tǒng)的長(zhǎng)周期變化規(guī)律.符號(hào)動(dòng)力學(xué)方法利用提取時(shí)間序列的長(zhǎng)周期特征實(shí)現(xiàn)早期故障檢測(cè)，符號(hào)化映射能實(shí)現(xiàn)信號(hào)降噪.字符序列的統(tǒng)計(jì)量能同時(shí)分析信號(hào)的長(zhǎng)周期與短周期變化細(xì)節(jié).利用D階馬爾科夫過(guò)程定義字母符號(hào)序列的固有模式，提取非線性系統(tǒng)的周期性特征.因此，基于符號(hào)動(dòng)力學(xué)的特征提取方法能夠簡(jiǎn)單、快速的處理非線性系統(tǒng)的數(shù)據(jù)，并提取非線性系統(tǒng)的周期性特征，避免了復(fù)雜的非線性方程求解.

2.1 非線性系統(tǒng)的符號(hào)化映射

假設(shè)一個(gè)連續(xù)隨機(jī)系統(tǒng)的物理過(guò)程可以利用如下方程表示：

(3)

(4)

最終，通過(guò)字符集合把一個(gè)時(shí)間序列信號(hào)分割為不同的子區(qū)間序列，每個(gè)子區(qū)間通過(guò)一個(gè)字母表示，如式(4)所示，這種映射也叫動(dòng)態(tài)系統(tǒng)符號(hào)化映射.使得一個(gè)連續(xù)隨機(jī)的時(shí)間序列通過(guò)字母符號(hào)化進(jìn)行離散變換，變成一組不同字母組合的符號(hào)序列.

時(shí)間序列數(shù)據(jù)通過(guò)子區(qū)間進(jìn)行分割，相空間的信號(hào)由于離散而丟失一部分系統(tǒng)信息.這類(lèi)丟失的信息可能是測(cè)量噪聲、誤差或者初始條件引起的變異信息.但字母組合能夠保留系統(tǒng)的主要特征，例如，相軌跡的周期性和吸引子等特征.

2.2 字符序列的特征提取

針對(duì)一串連續(xù)的符號(hào)序列，需要定義這串序列的變化規(guī)律，通常有兩種機(jī)器學(xué)習(xí)方法[16]，主要有ε機(jī)器學(xué)習(xí)和D階馬爾科夫機(jī)器學(xué)習(xí)方法.本文選擇D階馬爾科夫機(jī)器學(xué)習(xí)方法提取符號(hào)序列的固有特征的主要原因是利用D階馬爾科夫鏈描述系統(tǒng)的狀態(tài)演變過(guò)程會(huì)使得符號(hào)序列的特征向量具有相同的維度，從而使得異常程度或者故障程度的計(jì)算相對(duì)簡(jiǎn)單.

考慮一組字符串序列包含了系統(tǒng)的某一規(guī)律(周期性)，D階馬爾科夫機(jī)器學(xué)習(xí)方法可以定義系統(tǒng)的有效狀態(tài)(周期性轉(zhuǎn)移的有效狀態(tài)).某一周期內(nèi)的字符串組合的長(zhǎng)度看作D∈N，且字符的獨(dú)立不重復(fù)組合定義如下：

(5)

其中，狀態(tài)轉(zhuǎn)移的概率計(jì)算公式如下：

(6)

狀態(tài)轉(zhuǎn)移概率是有效狀態(tài)qj=si1…siD向有效狀態(tài)qk=si1…siDs轉(zhuǎn)移而出現(xiàn)的可能性.

2.3 字符個(gè)數(shù)的確定

符號(hào)個(gè)數(shù)的選擇對(duì)于符號(hào)動(dòng)力學(xué)系統(tǒng)建模至關(guān)重要，最優(yōu)的字符個(gè)數(shù)能夠幫助符號(hào)動(dòng)力學(xué)模型更準(zhǔn)確地提取系統(tǒng)的非線性特征，同時(shí)有效地降低噪聲的干擾；較少的字符個(gè)數(shù)導(dǎo)致系統(tǒng)特征的細(xì)節(jié)丟失，但是太多的字符個(gè)數(shù)會(huì)導(dǎo)致信息冗余，且浪費(fèi)計(jì)算資源.本文采用一種基于熵值變化率的指標(biāo)來(lái)確定字符個(gè)數(shù)，使得字符個(gè)數(shù)取值達(dá)到最優(yōu)，如圖2所示.

(7)

式中：pi為字符si出現(xiàn)的概率，且有H(1)=0.通過(guò)熵的變化率h(k)選擇合理的字符個(gè)數(shù)[17]，即

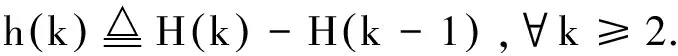
(8)

圖2 基于熵值變化率的字符個(gè)數(shù)選擇

h是一個(gè)量綱一的變量，從圖2中可以看出：熵值的變化率會(huì)隨著字符個(gè)數(shù)的增加單調(diào)遞減，表明字符個(gè)數(shù)的增加會(huì)降低熵值的變化率.雖然較低的熵值變化率使得模型能夠更加準(zhǔn)確的提取系統(tǒng)的微弱變化，但同時(shí)會(huì)增加故障檢測(cè)的計(jì)算量.微弱故障檢測(cè)能力與模型的計(jì)算量需要平衡，最優(yōu)的字符個(gè)數(shù)才能夠使算法的性能最優(yōu).因此，字符個(gè)數(shù)的選擇應(yīng)該使得熵值變化率相對(duì)較小，且用較少的字符.本文設(shè)置熵值變化率的閾值為εh=0.1，相應(yīng)的字符個(gè)數(shù)為9.

2.4 字符序列的故障檢測(cè)原理分析

假設(shè)電流信號(hào)服從杜芬方程的變化規(guī)律，且字符個(gè)數(shù)選取4.則字符a、b、c、d分別代表了正常信號(hào)的字符區(qū)間，而a′、b′、c′、d′則分別代表了故障信號(hào)的字符區(qū)間.故障參數(shù)θ能夠引起電流信號(hào)幅值、周期的微弱變化，從而導(dǎo)致故障信號(hào)的字符區(qū)間發(fā)生變異，與故障對(duì)應(yīng)的電流字符序列會(huì)重新組合.

例如：在圖3中，選取某一段電流信號(hào).根據(jù)式(4)，將健康狀態(tài)的電流數(shù)據(jù)轉(zhuǎn)換為對(duì)應(yīng)的字符序列“dccccccd”，而故障狀態(tài)的電流數(shù)據(jù)轉(zhuǎn)換為對(duì)應(yīng)的字符序列“d′c′c′b′b′c′c′d′”.字符序列已經(jīng)重新組合.因此，重新組合的字符序列能夠反映電流信號(hào)的故障.

圖3 字符序列的重新組合

2.5 飛輪故障檢測(cè)算法的流程圖

雖然狀態(tài)轉(zhuǎn)移矩陣能夠定義系統(tǒng)的行為，但是健康與故障狀態(tài)下的差異性難以通過(guò)狀態(tài)轉(zhuǎn)移矩陣的計(jì)算加以區(qū)分.而狀態(tài)轉(zhuǎn)移矩陣中具有單位值的概率特征向量能夠代表系統(tǒng)的固有特征.因此，本文用向量的距離代替兩個(gè)矩陣的距離.實(shí)際信號(hào)由于噪聲干擾以及系統(tǒng)動(dòng)態(tài)變化的影響，不同時(shí)間段的樣本所對(duì)應(yīng)的字符概率特征向量肯定存在一定的差異性，健康狀態(tài)的字符概率特征向量之間的差異性需要定義一個(gè)合理的閾值.待測(cè)狀態(tài)的字符概率特征向量在該范圍內(nèi)變化視為正常，否則故障.通過(guò)下式就能合理反映不同健康狀態(tài)之間的差異.

式中：pH為健康數(shù)據(jù)的字符概率特征向量(symbol probability vector) ；pT為測(cè)試數(shù)據(jù)的字符概率特征向量；δ反映了健康數(shù)據(jù)與測(cè)試數(shù)據(jù)之間的字符概率距離.因此，飛輪系統(tǒng)的符號(hào)動(dòng)力學(xué)故障檢測(cè)方法的流程如圖4所示.

Step 1 非線性系統(tǒng)的輸入會(huì)引起系統(tǒng)狀態(tài)的改變，不同的激勵(lì)信號(hào)使得系統(tǒng)的正常特征產(chǎn)生較大的波動(dòng).結(jié)合式(1)、(2)，利用Simulink仿真模型獲取飛輪系統(tǒng)在指定工作狀態(tài)下的電流信號(hào)序列集合.

Step 2 信號(hào)分類(lèi).主要是調(diào)整故障參數(shù)幅值，當(dāng)故障偏差幅值取零時(shí)，假定為系統(tǒng)健康數(shù)據(jù)；當(dāng)故障偏差幅值增大時(shí)，假定為測(cè)試數(shù)據(jù).

Step 3 狀態(tài)轉(zhuǎn)移矩陣通過(guò)式(6)獲取，式(7)計(jì)算狀態(tài)轉(zhuǎn)移矩陣的熵，式(8)計(jì)算狀態(tài)轉(zhuǎn)移矩陣的熵值相對(duì)于字符個(gè)數(shù)的變化率.根據(jù)圖2確定最優(yōu)的字符個(gè)數(shù).

Step 4 字符概率特征向量的閾值能反映健康狀態(tài)的擾動(dòng)范圍.式(9)能夠反映兩個(gè)字符概率特征向量之間的距離.簡(jiǎn)稱(chēng)字符概率距離.而這種距離是基于狀態(tài)轉(zhuǎn)移矩陣的熵，它的大小與系統(tǒng)噪聲有一定的關(guān)系.因此，閾值設(shè)置應(yīng)參考熵率的取值.

Step 5 利用式(10)實(shí)現(xiàn)飛輪系統(tǒng)的故障檢測(cè)，當(dāng)δ大于閾值時(shí)，飛輪系統(tǒng)出現(xiàn)故障；否則，飛輪系統(tǒng)正常.

圖4 飛輪系統(tǒng)的符號(hào)動(dòng)力學(xué)故障檢測(cè)流程

Fig.4 The fault detection of flywheel system based on symbolic dynamic filter

由于字符概率距離是一種向量的距離，本文選擇余弦的反函數(shù)，描述健康字符概率特征向量與故障字符概率特征向量之間的距離，計(jì)算公式如下：

(9)

式中，〈x,y〉是向量x與y的內(nèi)積，而 ‖x‖2是向量x的歐拉距離.與傳統(tǒng)的歐拉距離相比，利用向量夾角的反余弦值能準(zhǔn)確、直觀地反映微弱故障與正常狀態(tài)之間的差異性.距離指標(biāo)M反映了故障信號(hào)序列的長(zhǎng)周期偏離正常信號(hào)序列的嚴(yán)重程度.

對(duì)多個(gè)正常狀態(tài)的時(shí)間序列(健康數(shù)據(jù)樣本集合)進(jìn)行符號(hào)化映射，能夠得到一系列字符概率距離.這個(gè)距離反映了正常狀態(tài)偏離期望狀態(tài)的程度.對(duì)字符概率特征向量距離的集合進(jìn)行分析，取最大值作為該指標(biāo)的閾值.當(dāng)新獲取的測(cè)試數(shù)據(jù)屬于正常狀態(tài)時(shí)，滿足下式所定義的條件.否則，測(cè)試數(shù)據(jù)為故障數(shù)據(jù).

(10)

M是量綱一的變量.然而，系統(tǒng)噪聲使得健康數(shù)據(jù)在一定范圍內(nèi)波動(dòng).字符概率距離的閾值Mε與系統(tǒng)內(nèi)部參數(shù)變化無(wú)關(guān)，閾值設(shè)置應(yīng)該考慮系統(tǒng)噪聲的影響.這種不確定性導(dǎo)致字符概率距離存在一定的波動(dòng).字符個(gè)數(shù)越少，符號(hào)動(dòng)力學(xué)模型的降噪能力越強(qiáng)，對(duì)應(yīng)的字符概率閾值越小；而字符個(gè)數(shù)越多，符號(hào)動(dòng)力學(xué)模型的降噪能力變?nèi)酰瑢?duì)應(yīng)的字符概率閾值越大.參考熵值的變化率，這里選擇Mε=0.1.

3 飛輪系統(tǒng)的故障檢測(cè)

小衛(wèi)星由于體積的限制，只能布置少量的系統(tǒng)觀測(cè)點(diǎn)，衛(wèi)星系統(tǒng)中重要的部件至少有一個(gè)狀態(tài)觀測(cè)變量，這類(lèi)重要的觀測(cè)量包含系統(tǒng)的早期故障特征.工程中常見(jiàn)的故障檢測(cè)方法是單變量閾值檢測(cè)方法，單變量故障檢測(cè)具有簡(jiǎn)單、快速的優(yōu)點(diǎn)，數(shù)據(jù)存儲(chǔ)少，實(shí)時(shí)性強(qiáng)，適用于星載計(jì)算機(jī)，能夠完成衛(wèi)星實(shí)時(shí)在線的故障檢測(cè)、診斷.

符號(hào)動(dòng)力學(xué)[18]能用于非線性系統(tǒng)的異常檢測(cè)或者早期故障的預(yù)測(cè)分析.符號(hào)動(dòng)力學(xué)[19]計(jì)算簡(jiǎn)單、快速，對(duì)數(shù)據(jù)量要求小，能夠有效分析復(fù)雜非線性系統(tǒng)的變化規(guī)律.而飛輪的控制方程也可以看作一個(gè)非線性方程，電流信號(hào)就能反映飛輪系統(tǒng)的動(dòng)態(tài)變化過(guò)程.

飛輪的轉(zhuǎn)速始終通過(guò)電流驅(qū)動(dòng)，當(dāng)飛輪系統(tǒng)出現(xiàn)故障時(shí)，飛輪轉(zhuǎn)速會(huì)產(chǎn)生異常擾動(dòng)，但閉環(huán)控制會(huì)通過(guò)電流的增加或者減少實(shí)現(xiàn)目標(biāo)轉(zhuǎn)速的擾動(dòng)補(bǔ)償.因此，衛(wèi)星動(dòng)量輪的異常檢測(cè)主要針對(duì)飛輪的電流信號(hào).本文的指定工作狀態(tài)：小衛(wèi)星在姿態(tài)保持過(guò)程中，為了抵抗空間干擾力矩的作用，衛(wèi)星利用飛輪的動(dòng)量矩交換實(shí)現(xiàn)衛(wèi)星姿態(tài)的保持，飛輪轉(zhuǎn)速將圍繞目標(biāo)轉(zhuǎn)速波動(dòng).飛輪的電流能夠反映系統(tǒng)的異常擾動(dòng).此過(guò)程中設(shè)置了飛輪電機(jī)增益變小與飛輪摩擦力力矩增大的故障.為了體現(xiàn)微弱故障檢測(cè)能力，仿真給出了5個(gè)不同故障幅值的故障數(shù)據(jù).

飛輪閉環(huán)系統(tǒng)為一個(gè)速度反饋系統(tǒng)(圖5)，確保目標(biāo)轉(zhuǎn)速的魯棒性，但同時(shí)增加故障檢測(cè)的難度.系統(tǒng)包括：飛輪開(kāi)環(huán)模型、飛輪轉(zhuǎn)速PID控制器和飛輪數(shù)據(jù)采集系統(tǒng).

圖5 飛輪閉環(huán)系統(tǒng)框圖

飛輪轉(zhuǎn)速控制器的(PID)參數(shù)設(shè)置：比例系數(shù)0.1、積分系數(shù)0.1、微分系數(shù)0.1；系統(tǒng)仿真過(guò)程中，電機(jī)電流、飛輪轉(zhuǎn)速的初始值取0，其他對(duì)應(yīng)的物理參數(shù)選取無(wú)故障時(shí)相應(yīng)的取值；仿真系統(tǒng)的步長(zhǎng)0.01s，仿真時(shí)間為400s，故障發(fā)生時(shí)間是200s，一次采樣40 000點(diǎn).

3.1 電機(jī)增益變小故障

如圖6所示，第1段數(shù)據(jù)為飛輪電流的健康數(shù)據(jù)，飛輪的電機(jī)增益變小故障仿真5次，一共有6個(gè)觀測(cè)數(shù)據(jù)，為對(duì)比分析，6段數(shù)據(jù)放在同一圖中.電機(jī)增益參數(shù)的故障幅值為健康取值的比例分別為：1.00、0.99、0.95、0.90、0.70、0.50，對(duì)應(yīng)的故障參數(shù)偏差幅值分別為：0、0.01、0.05、0.10、0.30、0.50.由于飛輪在健康狀態(tài)下存在一定的動(dòng)態(tài)調(diào)整過(guò)程，使得電流信號(hào)存在一個(gè)階躍變化，而為了檢測(cè)幅值更小的故障，需要消除這類(lèi)正常擾動(dòng)的影響.因此，符號(hào)動(dòng)力學(xué)模型只分析電流從50～400s之間的數(shù)據(jù)，即相對(duì)穩(wěn)定的數(shù)據(jù).采樣點(diǎn)數(shù)為35 000，6段數(shù)據(jù)共有210 000個(gè)點(diǎn).

根據(jù)圖6所示，第1、2段數(shù)據(jù)的差異性非常微弱，難以區(qū)分.主要是噪聲力矩使得電流信號(hào)存在正常的波動(dòng)范圍，故障引起的波動(dòng)與噪聲引起的波動(dòng)相差微弱，導(dǎo)致兩種狀態(tài)難以區(qū)分；而第5、6段的數(shù)據(jù)明顯超出了電流正常的波動(dòng)范圍，但是通過(guò)閉環(huán)控制的調(diào)整，電流又回到正常的波動(dòng)范圍.因此，隨著故障偏差幅值的增加，在故障初期的電流階躍擾動(dòng)越來(lái)越明顯，但又快速回到正常波動(dòng)范圍，使得故障狀態(tài)與正常狀態(tài)難以區(qū)分.

圖6 電機(jī)增益變小故障的飛輪電流

根據(jù)飛輪系統(tǒng)符號(hào)動(dòng)力學(xué)故障檢測(cè)模型的流程圖(圖4)，計(jì)算健康狀態(tài)與故障狀態(tài)的字符概率距離，具體的計(jì)算結(jié)果如圖7所示. 隨著故障偏差幅值的增加，對(duì)應(yīng)的字符概率距離變大.由于第5、6段數(shù)據(jù)的故障差異性更加明顯，導(dǎo)致對(duì)應(yīng)的字符概率距離比其余故障的字符概率距離大.

基于擴(kuò)展卡爾曼濾波[7]的故障檢測(cè)方法將飛輪的故障檢測(cè)視為系統(tǒng)參數(shù)辨識(shí)與跟蹤問(wèn)題.為便于計(jì)算，將式(1)表示為線性離散狀態(tài)空間的時(shí)變形式.在物理建模的過(guò)程中忽略飛輪系統(tǒng)的3個(gè)非線性函數(shù)，并將飛輪的非線性函數(shù)簡(jiǎn)化為

(11)

(12)

式(12)中給出了飛輪系統(tǒng)的物理參數(shù)與系數(shù)矩陣的對(duì)應(yīng)關(guān)系.飛輪故障檢測(cè)的目標(biāo)是識(shí)別矩陣系數(shù)F中的物理參數(shù).電機(jī)增益變小的故障相當(dāng)于磁通量變小的故障.圖8是飛輪增益變小故障的檢測(cè)結(jié)果，在圖8中，可以看到物理參數(shù)的取值通過(guò)飛輪的3個(gè)變量可以得到實(shí)時(shí)跟蹤.故障偏差幅值設(shè)為0.1.

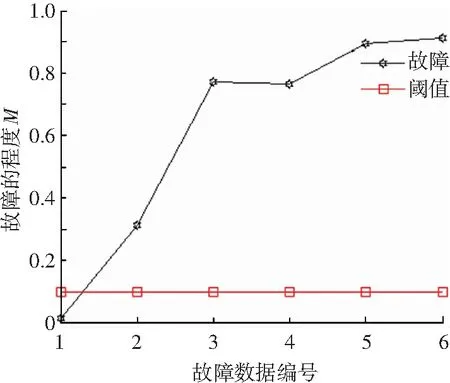
圖7 電機(jī)增益故障的檢測(cè)結(jié)果

圖8 擴(kuò)展卡爾曼濾波算法的故障檢測(cè)結(jié)果

3.2 摩擦力力矩增大故障

如圖9所示，第1段數(shù)據(jù)為飛輪電流的健康數(shù)據(jù)，飛輪的電機(jī)增益故障采集了5次，一共有6個(gè)觀測(cè)數(shù)據(jù)，為對(duì)比分析，將6段數(shù)據(jù)放在同一圖中.電機(jī)摩擦力力矩參數(shù)的故障幅值為健康取值的比例分別為：1.00、1.01、1.05、1.10、1.30、1.50，對(duì)應(yīng)的故障參數(shù)偏差幅值分別為：0、0.01、0.05、0.10、0.30、0.50.由于飛輪在健康狀態(tài)下存在動(dòng)態(tài)調(diào)整過(guò)程，使得電流信號(hào)存在一個(gè)階躍變化，而為了檢測(cè)幅值更小的故障，需要消除這類(lèi)正常擾動(dòng)的影響.因此，符號(hào)動(dòng)力學(xué)模型只分析電流從50～400 s之間的數(shù)據(jù)，即相對(duì)穩(wěn)定的數(shù)據(jù).采樣點(diǎn)數(shù)為35 000.6段數(shù)據(jù)共有210 000個(gè)點(diǎn).

根據(jù)圖10所示，第2、3、4段數(shù)據(jù)與第1段數(shù)據(jù)的差異性非常的微弱,難以區(qū)分.對(duì)比圖9與圖6的電流變化，電機(jī)增益變小故障直接影響飛輪電流，而摩擦力矩增大故障是通過(guò)轉(zhuǎn)速變化間接影響飛輪電流.當(dāng)故障幅值足夠大時(shí)，電機(jī)電流超出了健康狀態(tài)的波動(dòng)范圍.閉環(huán)控制為了抑制摩擦力力矩增大故障的影響，飛輪只能增加電流輸出.因此，摩擦力矩增大故障能夠顯著的增加飛輪系統(tǒng)的能耗，對(duì)系統(tǒng)危害更大.從圖9的第6、7段數(shù)據(jù)可以看到：異常擾動(dòng)的電流不能回到正常的波動(dòng)范圍.隨著故障偏差幅值的增加，電流的擾動(dòng)幅值增加.故障狀態(tài)與正常狀態(tài)之間的差異性更明顯.

圖9 摩擦力力矩增大故障的飛輪電流

根據(jù)飛輪系統(tǒng)符號(hào)動(dòng)力學(xué)故障檢測(cè)模型的流程圖(圖4)，計(jì)算健康狀態(tài)與故障狀態(tài)的字符概率距離，具體的計(jì)算結(jié)果如圖10所示. 隨著故障偏差幅值的增加，對(duì)應(yīng)的字符概率距離變大.

圖10 摩擦力力矩故障的檢測(cè)結(jié)果

對(duì)比圖7與圖10的字符概率距離，都超出了閾值控制線Mε=0.1，本文所提的方法能夠檢測(cè)飛輪的微弱故障或者早期故障.此外，早期故障的物理模型難以獲取，而相關(guān)的觀測(cè)數(shù)據(jù)卻容易得到，對(duì)于實(shí)際問(wèn)題中的早期故障，基于數(shù)據(jù)的方法比基于模型的方法更適合早期故障檢測(cè)的研究.

摩擦力矩增大的故障相當(dāng)于摩擦力矩系數(shù)增大的故障，圖11是飛輪系統(tǒng)摩擦力力矩增大故障的檢測(cè)結(jié)果,故障偏差幅值設(shè)為0.1.圖8的故障檢測(cè)結(jié)果要比圖11的故障檢測(cè)結(jié)果更準(zhǔn)確，主要原因是噪聲方差使得摩擦力矩參數(shù)估計(jì)值的方差變大.

圖11 擴(kuò)展卡爾曼濾波算法的故障檢測(cè)結(jié)果

3.3 對(duì)比分析

將該方法與本文方法進(jìn)行對(duì)比：首先，對(duì)比變量個(gè)數(shù)，該方法需要飛輪轉(zhuǎn)速、指令電壓、飛輪電流3個(gè)觀測(cè)量，而本文方法只需飛輪系統(tǒng)的電流信號(hào).其次，本文方法只關(guān)注飛輪的數(shù)據(jù)特征，而基于模型的方法注重算法的收斂度與精度分析，推導(dǎo)過(guò)程嚴(yán)密，在建模過(guò)程中需要忽略飛輪狀態(tài)方程的3個(gè)非線性項(xiàng).因此，當(dāng)求解的物理方程變?yōu)楦鼜?fù)雜的非線性方程時(shí)，求解過(guò)程會(huì)遇到較大的困難.最后，系統(tǒng)狀態(tài)方程的精確表達(dá)式在實(shí)際工程中很難精確獲取，而系統(tǒng)中變量的觀測(cè)數(shù)據(jù)相對(duì)容易獲取，工程應(yīng)用性強(qiáng).且本文算法的可移植性強(qiáng)，能夠用于衛(wèi)星其他部件的故障檢測(cè).

4 結(jié) 論

1)本文提出了一種基于字符概率特征向量的故障檢測(cè)方法.與基于模型的故障檢測(cè)方法對(duì)比分析，本文只需要單一變量的觀察數(shù)據(jù)進(jìn)行故障檢測(cè)，單變量故障檢測(cè)能夠減少觀測(cè)點(diǎn)的設(shè)置，降低衛(wèi)星系統(tǒng)的維護(hù)成本，且工程數(shù)據(jù)獲取比模型參數(shù)獲取相對(duì)容易.

2)本文算法是從數(shù)據(jù)中學(xué)習(xí)系統(tǒng)的行為，描述待測(cè)樣本偏離學(xué)習(xí)樣本的程度.因此，本文算法能夠避免復(fù)雜的數(shù)學(xué)建模，工程中易于實(shí)施.且算法的降噪能力強(qiáng)，具有可移植性、數(shù)據(jù)處理量大.本文算法具有簡(jiǎn)單、快速的優(yōu)點(diǎn)，適合星上實(shí)時(shí)的故障檢測(cè).

[1] 周東華, 劉洋, 何瀟. 閉環(huán)系統(tǒng)故障診斷技術(shù)綜述[J]. 自動(dòng)化學(xué)報(bào), 2013, 39(11):1933-1943. DOI: 10.3724/SP.J.1004.2013.01933.

ZHOU Donghua, LIU Yang, HE Xiao. Review on fault diagnosis techniques for closed-loop systems[J]. ACTA Automatica Sinica, 2013, 39(11):1933-1943. DOI: 10.3724/SP.J.1004.2013.01933.

[2] CHANDOLA V, BANERJEE A, KUMAR V. Anomaly detection: A survey [J]. ACM Computing Surveys (CSUR), 2009, 41(3):1-58. DOI: 10.1145/1541880.1541882.

[3] ZHANG Aihua, HU Qinglei, ZHANG Youmin. Observer-based attitude control for satellite under actuator fault[J]. Journal of Guidance, Control, and Dynamics, 2015, 38(4):806-811.DOI: 10.2514/1.G000625.

[4] WANG Zhenhua, SHEN Yi, ZHANG Xiaolei, et al. Fault diagnosis for satellite attitude control systems with four flywheels[J]. Journal of Dynamic Systems, Measurement, and Control, 2014, 136(4):0410161-0410164. DOI: 10.1115/1.4026515.

[5] SOBHANI-TEHRANI E, TALEBI H A, KHORASANI K. Hybrid fault diagnosis of nonlinear systems using neural parameter estimators[J]. Neural Networks, 2014, 50:12-32. DOI: 10.1016/j.neunet.2013.10.005.

[6] 曲春娣, 張洪鉞. 衛(wèi)星動(dòng)量輪閉環(huán)系統(tǒng)的UIO雙觀測(cè)器故障診斷[J]. 航天控制, 2005,23(6):66-71.DOI: 10.3969/j.issn.1006-3242.2005.06.016.

QU Chundi, ZHANG Hongyue. The fault diagnosis of momentum close-loop system used in satellite based on the UIO double observers[J]. Aerospace Control, 2005,23(6):66-71.DOI: 10.3969/j.issn.1006-3242.2005.06.016.

[7] 李知周, 張銳, 朱振才, 等. 基于擴(kuò)展卡爾曼濾波的動(dòng)量輪故障檢測(cè)方法[J]. 航空學(xué)報(bào), 2010, 31(8):1614-1621.

LI Zhizhou, ZHANG Rui, ZHU Zhencai, et al. Extended Kalman filter-based fault detection for momentum wheel[J]. ACTA Aeronautica et Astronautica Sinica, 2010, 31(8):1614-1621.

[8] 岑朝輝, 魏蛟龍, 蔣睿, 等. 基于綜合觀測(cè)器的執(zhí)行器過(guò)程故障量精確診斷[J]. 宇航學(xué)報(bào), 2011,32(6):1318-1326. DOI: 10.3873/j.issn.1000-1328.2011.06.018.

CEN Zhaohui, WEI Jiaolong, JIANG Rui, et al. Accurate diagnosis on process fault parameters of nonlinear actuator based on adaptive observer and extended state observer[J]. Journal of Astronautics, 2011,32(6):1318-1326.DOI: 10.3873/j.issn.1000-1328.2011.06.018.

[9] BELLALI B, HAZZAB A, BOUSSERHANE I K, et al. Parameter estimation for fault diagnosis in nonlinear systems by ANFIS[J]. Procedia Engineering, 2012, 29:2016-2021. DOI: 10.1016/j.proeng.2012.01.254.

[10]沈毅, 張攸磊, 王振華. 基于EMD和有向因子圖的航天器故障診斷[J]. 哈爾濱工業(yè)大學(xué)學(xué)報(bào), 2013,45(1):19-24.

SHEN Yi，ZHANG Xiaolei，WANG Zhenhua. Spacecraft fault diagnosis based on empirical mode decomposition and directed factor graph[J]. Journal of Harbin Institute of Technology, 2013,45(1):19-24.

[11]BAHRAMPOUR S, RAY A, SARKAR S, et al. Performance comparison of feature extraction algorithms for target detection and classification[J]. Pattern Recognition Letters, 2013, 34(16):2126-2134. DOI: 10.1016/j.patrec.2013.06.021.

[12]陳沖, 丁炯, 張宏, 等. 累積放電模型及其符號(hào)動(dòng)力學(xué)研究[J]. 物理學(xué)報(bào), 2013, 62(14):49-55.DOI:10.7498/aps.62.140502.

CHEN Chong, DING Jiong, ZHANG Hong, et al. Study of an integrate-and-discharge model with symbolic dynamics[J]. Acta Physica Sinica, 2013, 62(14):49-55.DOI:10.7498/aps.62.140502.

[13]王松嶺, 許小剛, 劉錦廉, 等. 基于符號(hào)動(dòng)力學(xué)信息熵與改進(jìn)神經(jīng)網(wǎng)絡(luò)的風(fēng)機(jī)故障診斷研究[J]. 華北電力大學(xué)學(xué)報(bào)(自然科學(xué)版), 2013,40(4): 51-58. DOI:10.3969/j.ISSN.1007-2691.2013.04.09.

WANG Songling, XU Xiaogang, LIU Jinlian, et al. Fault diagnosis of fan based on symbolic dynamics entropy and improved neural network[J]. Journal of North China Electric Power University,2013,40(4): 51-58. DOI:10.3969/j.ISSN.1007-2691.2013.04.09.

[14]厲海濤, 金光, 周經(jīng)倫, 等. 動(dòng)量輪在軌狀態(tài)可靠性貝葉斯網(wǎng)絡(luò)建模與評(píng)估[J]. 航空學(xué)報(bào), 2009,30(6):1084-1089. DOI: 10.3321/j.issn:1000-6893.2009.06.019.

LI Haitao, JIN Guang, ZHOU Jinglun, et al. Bayesian network reliability modeling and assessment of momentum wheel on orbit[J]. ACTA Aeronautica et Astronautica Sinica, 2009,30(6):1084-1089. DOI: 10.3321/j.issn:1000-6893.2009.06.019.

[15]ZHAO Shuping, KHORASANI K. A recurrent neural network based fault diagnosis scheme for a satellite[C]//Proceedings of the 33rd Annual Conference of the IEEE Industrial Electronics Society, IECON. Taipei: IEEE Computer Society, 2007: 2660-2665. DOI: 10.1109/IECON.2007.4459995.

[16]SHALIZI C R, SHALIZI K L, CRUTCHFIELD J P. An algorithm for pattern discovery in time series[R/OL]. (2002-10-29)[2002-11-27]. http://arxiv.org/abs/cs/0210025.

[17]RAJAGOPALAN V, RAY A. Symbolic time series analysis via wavelet-based partitioning[J]. Signal Processing, 2006, 86(11):3309-3320. DOI: 10.1016/j.sigpro.2006.01.014.

[18]RAJAGOPALAN V, CHAKRABORTY S, RAY A. Estimation of slowly varying parameters in nonlinear systems via symbolic dynamic filtering[J]. Signal Processing, 2008, 88(2):339-348. DOI: 10.1016/j.sigpro.2007.08.007.

[19]李洪偉, 周云龍, 任素龍, 等. 符號(hào)動(dòng)力學(xué)信息熵在氣液兩相流型電導(dǎo)信號(hào)分析中的應(yīng)用[J]. 化工學(xué)報(bào), 2012,63(11):3486-3492.DOI: 10.3969/j.issn.0438-1157.2012.11.015.

LI Hongwei, ZHOU Yunlong, REN Sulong, et al. Application of conductance signals analysis of gas-liquid two-phase flow patterns based on symbolic dynamics entropy[J]. CIESC Journal, 2012,63(11):3486-3492.DOI: 10.3969/j.issn.0438-1157.2012.11.015.

(編輯 張 紅)

A symbolic dynamic analysis of flywheel system for fault detection

WANG Rixin, GONG Xuebing, XU Minqiang, LI Yuqing

(School of Astronautics, Harbin Institute of Technology, Harbin 150001, China)

The fault detection method of symbolic dynamics is proposed to detect the tiny faults of flywheels. Firstly, the symbolic dynamics algorithm transforms the flywheel current into a series of symbols. The signal noise reduction and data compression can be accomplished by the symbol generation. Secondly, theD-Markov machine can define the abnormal transitions of symbol sequences and produce the probability state transition matrix. Then, the number of symbols is selected from the change in entropy of symbol sequences. Moreover, the symbol probability vector can be obtained according to the eigenvector of the probability state transition matrix. The threshold of distance among the symbol probability vectors can be used to detect the faults of the flywheel. Finally, The simulation results show this method can identify varying degrees of faults in the flywheel and achieve the tiny fault detection by the distance among the vectors. Compared with the extended Kalman filter method, the proposed method can detect the faults of flywheel by using the single variable without the complicated kinetic modeling. The proposed fault detection method in this paper can be also used in the other components of satellites, which can learn the system behavior from process data and have the merit of portability.

symbolic dynamics; flywheel system; finite-state automaton; fault detection; extended kalman filtering

10.11918/j.issn.0367-6234.2016.10.004

2015-05-27

國(guó)家自然科學(xué)基金( 61203151);國(guó)家重點(diǎn)基礎(chǔ)研究發(fā)展計(jì)劃( 973 計(jì)劃) (2012CB720003);航天器在軌故障診斷與維修重點(diǎn)實(shí)驗(yàn)室開(kāi)放課題資助(SDML-OF2015003)

王日新(1963—)男，副教授；

徐敏強(qiáng)(1960—)男，教授，博士生導(dǎo)師

龔學(xué)兵，gongdanumber1@163.com

TP274

A

0367-6234(2016)10-0031-08