可規定性能的輸入受限非線性系統反步控制
王永超,張勝修,扈曉翔,曹立佳,孫維超
(1.火箭軍工程大學 控制工程系,西安710025;2.哈爾濱工業大學 智能控制與系統研究所,哈爾濱150001)
?
可規定性能的輸入受限非線性系統反步控制
王永超1,張勝修1,扈曉翔1,曹立佳1,孫維超2
(1.火箭軍工程大學 控制工程系,西安710025;2.哈爾濱工業大學 智能控制與系統研究所,哈爾濱150001)
針對具有不可直接測量狀態和控制方向未知的輸入受限非線性系統的跟蹤問題,提出一種基于模糊狀態觀測器的反步控制方法.首先采用模糊狀態觀測器估計被控系統中的不可測量狀態;然后利用具有光滑特性的雙曲正切函數和Nussbaum增益函數對控制器的飽和問題進行處理,根據可規定誤差面性能技術對輸出跟蹤誤差的邊界進行限定;最后將反步法和動態面法相結合設計魯棒控制器.運用Lyapunov理論對系統的穩定性能進行了分析,證明閉環系統的所有信號最終半全局一致有界.以具有參數不確定性和存在外界未知有界干擾的高超聲速飛行器縱向運動為仿真模型,仿真結果驗證了所提算法的有效性.
可規定性能;模糊狀態觀測器;輸入受限;反步法;高超聲速飛行器
近年來針對輸入受限問題出現了一系列的研究成果.文獻[1-2]分別針對飛行控制中執行機構飽和的問題,采用解耦線性控制方法設計了飛控系統.文獻[3]利用LMI區域法對抗飽和中D穩定問題進行了比較深入的研究.文獻[4]提出了SISO系統的指令濾波反步控制方法,較好地解決系統狀態與控制信號受限情況下的穩定控制問題.文獻[5]利用多層神經網絡逼近控制律的飽和特性,該控制策略能夠有效地處理控制輸入飽和受限的約束,在完成控制目標的同時,具有良好的過渡過程品質.文獻[6]提出一種智能自適應滑模控制方法,利用神經網絡來逼近補償執行機構的飽和非線性.文獻[7-8]利用雙曲正切函數的光滑特性設計了反步控制器,并利用Nussbaum增益函數對飽和受限問題進行處理,其中系統的干擾利用神經網絡或干擾觀測器進行在線逼近.文獻[9]利用模型預測控制自身優勢,將輸入飽和視為待優化目標函數的一種約束條件,在此基礎上進行控制器的設計,取得了理想的效果.
以上研究成果在一定條件下均取得理想的效果,但是上述文獻都是基于控制系統狀態可直接測量這個假設基礎之上的,對于控制系統中狀態不可直接測量的情況少有研究.而在實際的控制系統中,狀態不可直接測量的情況也是十分常見的,在這種情況下,需要一種基于狀態觀測器的控制方案.
反步法[10](backstepping)是解決非線性系統控制問題的一種行之有效的方法.其基本思想是將復雜的高階非線性系統分解成一系列的低階系統,通過由后至前反復為每個子系統設計Lyapunov函數和虛擬控制變量,直到完成整個控制系統的設計.傳統的反步法在設計控制器的過程當中,虛擬控制變量反復求導,并且伴隨著階數的增加,計算量呈指數增長,也就是所謂的“計算膨脹”.文獻[11]引入了動態面法,也即是將設計的輔助虛擬控制變量通過一階積分濾波器,避免了求導這個復雜過程.
本文采用模糊邏輯系統(Fuzzy logic system,FLS)逼近系統中含有不確定參數和未知有界干擾的非線性函數,并由此來構建模糊狀態觀測器,利用具有光滑特性的雙曲正切函數和Nussbaum增益函數處理系統中的輸入飽和受限問題,并結合可規定跟蹤誤差面性能技術運用Backstepping法設計一種有效處理輸入受限的輸出反饋自適應控制方案.
1 問題描述
考慮如下所示的一類SISO非線性系統:
(1)
式中:xi(t)=[x1(t),…,xi(t)]T∈Ri為系統的狀態向量;u(v(t))∈R為系統受執行器飽和特性影響的輸出;v(t)∈R為執行器的輸入;y(t)∈R為系統的輸出量;fi(·)、gi(·)分別為包含不確定參數的光滑非線性函數;di(t)為系統受到的外界干擾變量.為敘述方便,文中將xi(t)記為xi,其余變量作類似處理.
式(1)中的飽和受限函數具體表達形式如下:
式中uM為受限函數的界限值,這在一些工業控制應用中值是已知的.
考慮到雙曲正切函數對飽和受限函數的近似逼近性質,上述所示的飽和受限函數等價于如下形式:

式中:h(·)為雙曲正切函數,d(v)=sat(v)-h(v)為有界函數,界限值表示為
則式(1)可變換為如下形式:
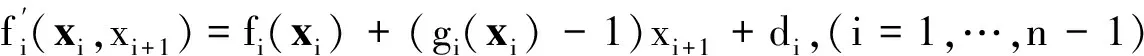
在本文中,假設只有輸出y是可測量的.控制目標是設計模糊狀態觀測器和自適應控制方案使得系統能夠穩定跟蹤參考輸入信號yr,閉環系統所有信號半全局一致有界且跟蹤誤差滿足可規定的衰減動態性能.
為便于控制器的設計引入下列假設及引理.
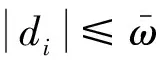
假設2[7]對于非線性系統(1),參考輸入信號yr及其一階導數存在且有界.
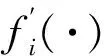
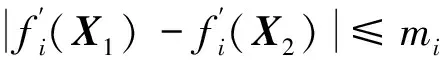
式中‖·‖表示向量的2-norm.
定義1 如果函數N(s)滿足以下條件:
則稱函數N(s)為Nussbaum增益函數.

式中:C、M、γχ>0分別為常數,ζ為正變量.
2 可規定誤差面性能
定義誤差面向量S(t)=[s1(t),…,sn(t)]T∈Rn,本文中可規定的性能是使系統誤差面si(t)嚴格按照如下所示的范圍衰減[13-14].
(2)
式中:設計參數δi,1,δi,2滿足0<δi,1,δi,2≤1,函數hi(t)為有界且單調遞減的光滑函數且具有如下特性:
式中hi,∞為常數.
引入誤差變換方程:
式中:?i(t)為變換誤差,Φi:(-δi,1,δi,2)→(-∞,∞)為嚴格遞增的光滑函數.文中采用如下變換函數:
式中ai>0為設計常數.
引理2[15]如果?i(t)有界,那么當t≥0時,誤差面si(t)滿足如式(2)所示的可規定衰減動態性能.
3 模糊狀態觀測器設計
3.1 模糊邏輯系統
根據文獻[16],帶有模糊規則庫(IF-THEN規則),乘積推理機,單值模糊器和中心平均解模糊器的模糊系統形式表示如下:
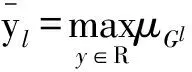
定義模糊基函數ξl如下:
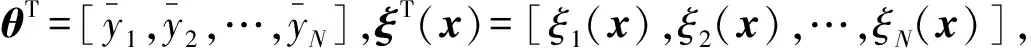
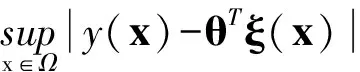
3.2 狀態觀測器
由于文中只有輸出y可測量,狀態變量x2,…,xn不可直接測量,故需要設計一狀態觀測器對其進行觀測.設計如下所示的模糊狀態觀測器[17]:

式中HL(s)為Butterworth低通濾波器(Low-passfilter,LPF)[18].

(3)
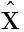
(4)
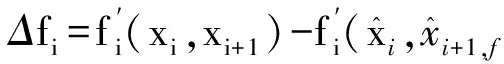
3.3 觀測器的穩定性分析
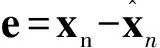
(5)
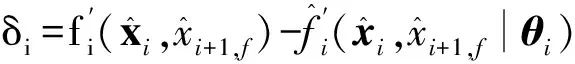
ATP+PA=-2Q.
(6)
選擇Lyapunov函數V0如下:

則函數V0關于時間t的導數為
(7)
將式(5)、(6)帶入式(7),得
(8)
式中λmin(Q)為正定矩陣Q的最小特征值;δ=[δ1,…,δn]T,ΔF=[Δf1,…,Δfn]T.
根據Young不等式和假設3~5,可得:
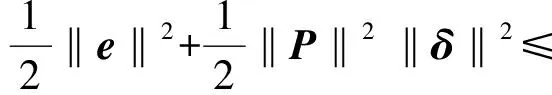
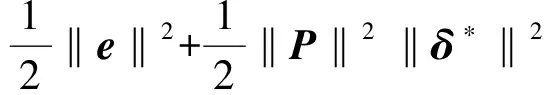
(9)
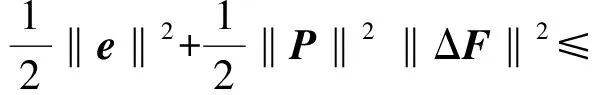


(10)

聯立式(8)~(10),得到:
(11)
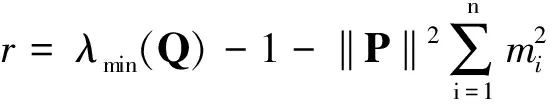

4 控制器設計及穩定性分析
本文將結合反步法和動態面法對控制系統進行設計.
Step 1 由于系統中狀態不可測量,系統中的反饋控制律不能直接利用其給出.模糊狀態觀測器設計中已經證明了建立的模糊狀態觀測器觀測誤差是收斂的,故觀測器狀態可以用于系統反饋控制律的設計,這與針對實際系統進行設計是等價的,因此定義如下:
式中αi-1為虛擬控制變量,具體形式由下文給出.
為了便于控制的設計,本文中只要求系統跟蹤參考信號的誤差滿足一定的可規定性能.
令s1=z1,則誤差變換函數?1關于時間t的導數為
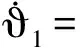
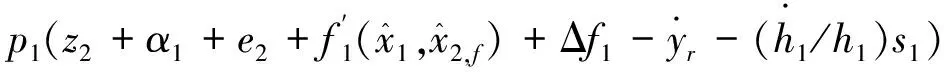
(12)
式中p1=a1((1/(s1+δ1,1h1))-(1/(s1-δ1,2h1))).
定義模糊系統最小逼近誤差ε1為
(13)

需要說明的是,根據文中所建立的Lyapunov函數導數性質和文中采用投影法確定參數的自適應律,可以保證參數有界,進而根據緊集上連續函數的性質,假設4和假設6成立是可以得到保證的.
將式(13)帶入式(12),得


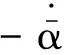
選擇Lyapunov函數V1為
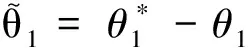
則函數關于時間t的導數為


(14)
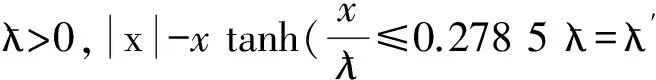
根據定理2,式(14)可變換為
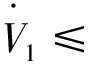
(15)
同時根據Young不等式,得
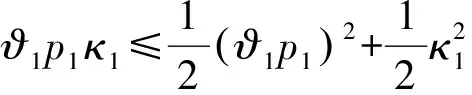
(16)
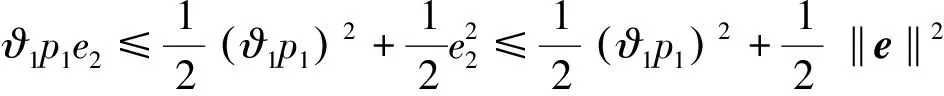
(17)
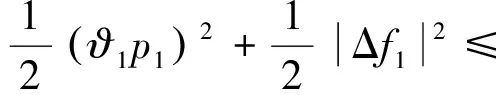
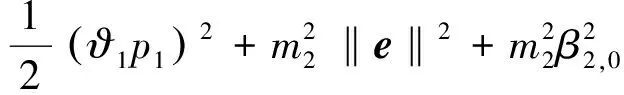
(18)
將式(16)~(18)帶入式(15),得

(19)
選取虛擬控制變量和參數的自適應律分別為
(21)
(22)
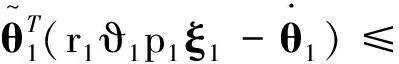
將式(20)~(22)帶入到式(19)中,得
(23)
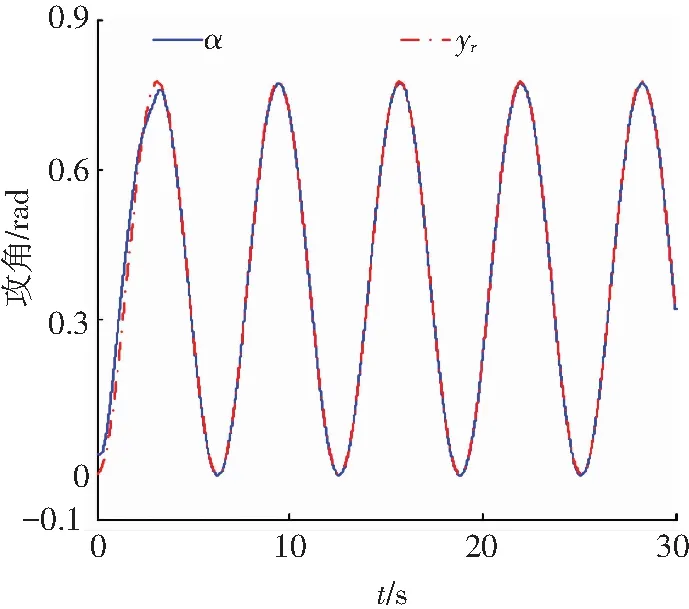
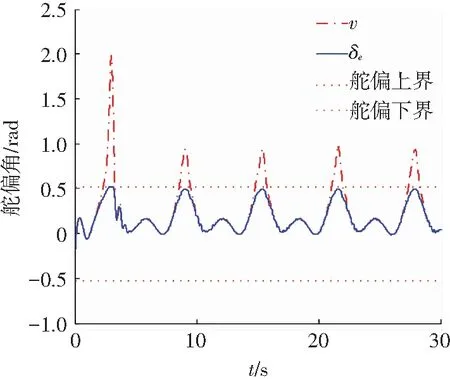
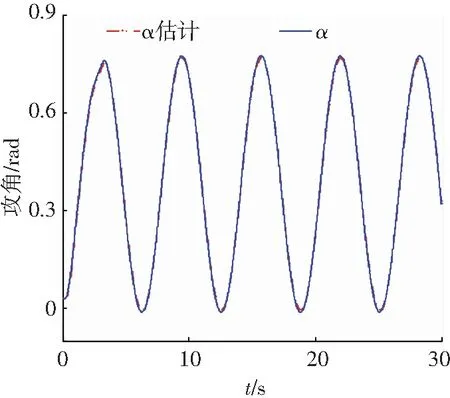
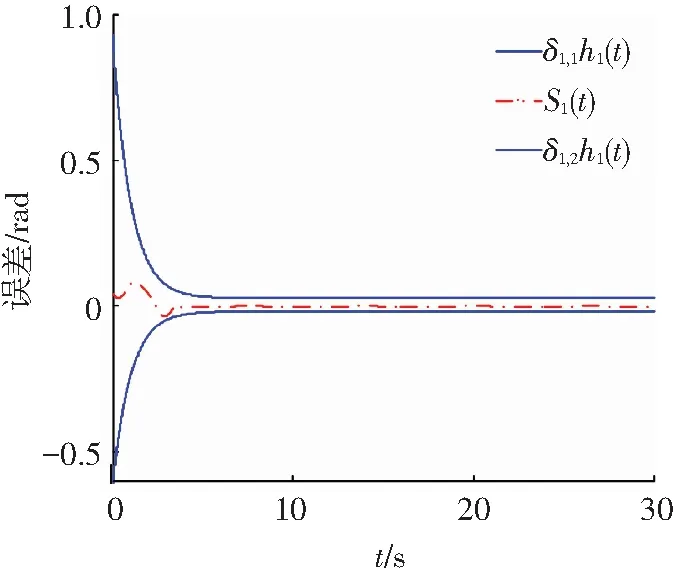
Step i(2≤i (24) 式中wi=εi-δi為模糊系統復合誤差. (25) 選擇Lyapunov函數Vi為 (26) 則函數Vi關于時間t的導數,并將式(24)、(25)帶入式(26)得 (27) 根據定理2和Young不等式,式(27)可化為 (28) (29) (30) (31) 將式(29)~(31)帶入到式(28)中,得 (32) (33) 參數的自適應律如式(30)、(31)所示,并將式(33)帶入式(28)中,得 (34) Step n 定義: zn關于時間t的導數為 (35) (36) 選擇Lyapunov函數Vn為 (37) 則函數Vn關于時間t的導數,并將式(35)、(36)帶入式(37)得 (38) 根據定理2和Young不等式,式(38)可轉化為 (39) 選取輔助虛擬控制變量和參數自適應律如下: (40) (41) (42) 將式(40)~(42)帶入到式(39)中,整理合并可得 (43) Step n+1 定義: (44) (45) (46) (47) 中間變量zn+1關于時間t的導數為 選擇Lyapunov函數Vn+1為 則函數Vn+1關于時間t的導數為 (48) 考慮到閉環系統所有信號的有界性,選擇Lyapunov函數Vsum如下: 對函數Vsum求導,并結合式(11)、(23)、(32)、(34)、(43)、(48)整理合并可得 (49) 則式(49)可轉化為 (50) 對式(50)進行積分,得 根據引理1可得Vsum(·)和χ(·)有界,且跟蹤誤差滿足如下不等式: 同時變量?1(t)有界,根據引理2可得,輸出跟蹤誤差滿足衰減動態性能. 故根據以上控制器的設計過程和對閉環系統穩定性分析,可得到以下定理 . 定理3 對于滿足假設1~5的輸入受限非線性系統(1),設計模糊狀態觀測器(3),設計控制器(44)~(46),設計系統輔助虛擬控制變量(20)、(29)、(33)、(40),選取參數自適應律(21)~(22)、(30)~(31)、(41)~(42),則閉環系統所有信號半全局一致有界(SGUUB),并且輸出跟蹤誤差滿足可規定衰減動態性能. 由于高超聲速飛行器超高的飛行速度和特殊的飛行環境,相比于傳統飛行器具有較強的參數不確定和較大的外界干擾,且飛行動力系統對姿態特別是攻角側滑角具有非常嚴格的條件要求,控制系統的研究面臨前所未有的挑戰[21].為此需要設計魯棒性強,跟蹤誤差滿足一定要求的控制系統.同時由于高超聲速飛行器不菲的造價,因此也要求控制系統具有一定的可靠性(如系統中狀態量傳感器出現故障導致狀態不能直接測量的情況下,控制系統依然能夠實現對指令的穩定跟蹤).在飛行器進行機動飛行時由于執行器自身物理構造的限制,導致執行器出現飽和的情況.如果不考慮這種輸入受限的情況,可能會導致系統動態性能變差,如調節時間增長、超調量增大、引起系統滯后和振蕩加劇,嚴重的將導致系統不穩定[22],因此在設計控制系統時也需要考慮執行器輸入受限這種情況.為驗證本文所提方法的有效性,選用一類有翼錐構型的吸氣式高超聲速飛行器作為仿真模型.飛行高度h=110 000 ft,速度v=15 060 ft/s,其縱向動態特性表示如下[23]: (51) 式中:α、q分別為飛行器的攻角和俯仰角速度;m、Iyy分別為質量和轉動慣量;L、T、Myy、d分別為升力、推力、俯仰力矩和俯仰軸上受到的外界干擾.上述系統中涉及的力與力矩的具體表達形式如下: CL=0.620 3α, CM(α)=-0.035α2+0.036 617(1+ΔCMα)α+5.326 1×10-6, CM(δe)=ce(δe-α), 文中假設推力不變,攻角的跟蹤控制通過舵偏角的偏轉來調節.飛行器的舵偏角是在一定的范圍內的,且飽和界限值(±30°)已知.采用正切函數處理飽和問題,令[x1,x2]T=[α,q]T,將式(51)等效為如下形式: 假設俯仰角速度測量傳感器在飛行的過程當中出現故障,無法實現精確測量,故采用本文中設計的基于模糊狀態觀測器的控制方法.本文中攻角的參考指令信號為yr=-22.5°cos(t)+22°. 按照本文方法設計如下所示的模糊狀態觀測器和反步控制器. 模糊狀態觀測器: 設計的控制器如下: 函數h1(t)=e-t+0.03,設計參數δ1,1=0.6,δ1,2=0.9,a1=0.02. 圖1為輸出響應曲線,其中圖1中虛線表示為參考輸入信號曲線,實線表示為跟蹤響應曲線.從圖1中可以看出在系統存在不確定性參數和未知外界干擾的情況下,攻角的輸出信號能夠穩定地跟蹤參考輸入信號. 圖1 輸出響應曲線 圖2為系統的控制信號曲線,虛線表示為設計的控制輸入信號,實線表示為執行器信號.從圖2中可以看出雖然控制輸入信號在一些情況下遠遠超出了界限值,但是執行器信號依然控制在飽和界限范圍內.圖3,4分別為模糊狀態觀測器的響應曲線.雖然俯仰角在外界干擾值很大的情況下,觀測效果不太理想,但是系統在輸入受限的情況下,依然能夠很好地跟蹤參考輸入信號.圖5為系統的跟蹤誤差曲線,虛線表示系統的跟蹤誤差.從圖5中可以清晰地看出,系統跟蹤誤差被限定在可規定性能范圍內. 圖2 控制信號 圖3 攻角觀測響應曲線 圖4 俯仰角觀測響應曲線 圖5 跟蹤誤差曲線 1)本文提出了一種有效處理具有不可直接測量狀態的輸入受限的不確定非線性系統的反步控制方法.運用Lyapunov理論對系統的穩定性進行分析,證明了閉環系統所有信號半全局一致最終有界(SGUUB). 2)利用雙曲正切函數和Nussbaum增益函數有效地處理了輸入飽和約束,并采用可規定誤差面性能技術對輸出跟蹤誤差進行了有效限定. 3)能夠有效地處理控制方向未知而引起的奇異等問題,并且文中對模糊系統的逼近誤差進行了自適應補償,進一步減小了跟蹤誤差. 4)仿真過程中,雖然模糊狀態觀測器對不可直接測量狀態的估計效果不是很理想,但系統依然能夠具有很好的跟蹤效果和很強的魯棒性能. [1]SIWAKOSITW,SNELLSA,HESSRA.Robustflightcontroldesignwithhandlingqualitiesconstraintsusingscheduledlineardynamicinversionandloop-shaping[J].IEEETransactionsonControlSystemsTechnology, 2000, 8(3): 483-494.DOI: 10.1109/87.845879. [2] JOHNSON E N, CALISE A J. Limitedauthority adaptive flight control for reusable launch vehicles[J]. Journal of Guidance, Control, and Dynamics, 2003, 26(6): 906-913. [3] HENCEY B, ALLEYNE A. An anti-windup technique for LMI regions[J]. Automatica, 2009, 45(10): 2344-2349. DOI: 10.1016/j.automatica.2009.06.021. [4] FARRELL J A, POLYCARPOU M, SHARMA M, et al. Commandfiltered backstepping[J]. IEEE Transactions on Automatic Control, 2009, 54(6): 1391-1395. DOI: 10.1109/TAC.2009.2015562.[5] 李靜,左斌,段洣毅,等. 輸入受限的吸氣式高超聲速飛行器自適應Terminal滑模控制[J]. 航空學報,2012, 33(2):220-233. DOI: 11-1929/V.201110T4.1505.003. LI Jing, ZUO Bin, DUAN Miyi, et al. Adaptive terminal sliding mode control for air-breathing hypersonic vehicles under control input constraints[J]. Acta Aeronautica ET Astronautica Sinica, 2012, 33(2):220-233. DOI: 11-1929/V.201110T4.1505.003. [6] 胡慶雷,張愛華,姜成平, 等. 控制受限的衛星軌道轉移過程中的姿態控制[J]. 哈爾濱工業大學學報,2013, 45(5):1-6. DOI: 10.11918/j.issn.0367-6234.2013.05.001. HU Qinglei,ZHANG Aihua,JIANG Chengping, et al. Attitude control of satellite in process of orbit transfer with constraint input[J]. Journal of Harbin Institute of Technology, 2013, 45(5):1-6. DOI: 10.11918/j.issn.0367-6234.2013.05.001. [7] WEN Changyun, ZHOU Jing, LIU Zhitao, et al. Robust adaptive of uncertain nonlinear systems in the presence of input saturation and external disturbance[J]. IEEE Transactions on Automatic Control, 2011, 56(7): 1672-1678. DOI: 10.1109/TAC.2011.2122730. [8] 周硯龍,陳謀. 基于干擾觀測器的輸入受限非線性系統魯棒控制[J]. 南京理工大學學報,2014, 38(1):40-47.DOI: 10.3969/j.issn.1005-9830.2014.01.007. ZHOU Yanlong, CHEN Mou. Robust control of nonlinear systems with input constraint based on disturbance observer[J]. Journal of Nanjing University of Science and Technology, 2011, 56(7): 1672-1678. DOI: 10.3969/j.issn.1005-9830.2014.01.007. [9] 孔小兵,劉向杰. 基于輸入輸出線性化的連續系統非線性模型預測控制[J]. 控制理論與應用,2012, 29(2):217-224. DOI: 10.7641/j.issn.1000-8152.2012.2.PCTA110510. KONG Xiaobing, LIU Xiangjie. Continuous-time nonlinear model predictive control with input/output linearization[J]. Control Theory & Applications, 2012, 29(2):217-224. DOI: 10.7641/j.issn.1000-8152.2012.2.PCTA110510. [10]KANELLAKOPOULOS I, KOKOTOVI P V, MORSE A S. Systematic design of adaptive controllers for feedbacklinearizable systems[J]. IEEE Transactions on Automatic Control, 1991, 36(11): 1241-1253. DOI: 10.1109/9.100933. [11]SWAROOP D, HEDRICK J K, YIP PP, et al. Dynamic surface control for a class of nonlinear systems[J]. IEEE Transactions on Automatic Control, 2000, 45(10): 1893-1899. DOI: 10.1109/TAC.2000.880994. [12]HUA Changchun, WANG Qingguo, GUAN Xinping. Adaptive fuzzy output feedback controller design for nonlinear time-delay systems with unknown control direction[J]. IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics, 2009, 39(2): 363-374. DOI: 10.1109/TSMCB.2008.2005204. [13]BECHLIOULIS C P, ROVITHAKIS G A. Prescribed performance adaptive control for multi-input multi-output affine in the control nonlinear systems[J]. IEEE Transactions on Automatic Control, 2010, 55(5): 1220-1226. DOI: 10.1109/TAC.2010.2042508. [14]XU Yinyin, TONG Shaocheng, LI Yongming. Prescribed performance fuzzy adaptive fault-tolerant control of non-linear systems with actuator faults[J]. IET Control Theory and Applications, 2014, 8(6): 420-431. DOI: 10.1049/iet-cta.2013.0676.[15]YOO S J. Fault-tolerant control of strict-feedback nonlinear time-delay systems with prescribed performance[J]. IET Control Theory and Applications, 2013, 7(11): 1220-1226. DOI: 10.1049/iet-cta.2013.0252.[16]WANG Lixin. Adaptive fuzzy systems and control: design and stability analysis[M]. New Jersey: Prentice-Hall, 1994. [17]TONG Shaocheng, LI Yongming. Observer-based adaptive fuzzy backstepping control of uncertain nonlinear pure-feedback systems[J]. Science China(Information Sciences), 2014, 57(1): 1-14. DOI: 10.1007/s11432-013-5043-y. [18]ZOU Anmin, HOU Zengguang, TAN Min. Adaptive control of a class of nonlinear pure-feedback systems using fuzzy backstepping approach[J]. IEEE Transactions on Fuzzy systems, 2008, 16(4): 886-897. DOI: 10.1109/TFUZZ.2008.917301. [19]KHALIL H K. Nonlinear systems[M]. 3rd ed. New Jersey: Prentice Hall, 2002. [20]PLOYCARPOU MM, IOANNOU P A. A robust adaptive nonlinear control design[J]. Automatica, 1996, 32(3): 423-427. DOI:10.1016/0005-1098(95)00147-6. [21]黃琳,段志生,楊劍影. 近空間高超聲速飛行器對控制科學的挑戰[J]. 控制理論與應用,2011,28(10): 1496-1505. DOI: 10.7641/j.issn.1000-8152.2011.10.025. HUANG Lin, DUAN Zhisheng, YANG Jianying. Challenges of control science in near space hypersonic aircrafts[J]. Control Theory & Applications,2011,28(10): 1496-1505. DOI: 10.7641/j.issn.1000-8152.2011.10.025. [22]CAMPO P J, MORARI M. Robust control of processes subject to saturation nonlinearities[J]. Computers & Chemical Engineering, 1990, 14(4/5): 343-358. DOI: 10.1016/0098-1354(90)87011-D.[23]XU Haojian, MIRMIRANI M D, IOANNOU P A. Adaptive sliding mode control for a hypersonic flight vehicle[J]. Journal of Guidance, Control, and Dynamics, 2004 27(5): 829-838. DOI: 10.2514/1.12596. (編輯 張 紅) Prescribed performance backstepping control of nonlinear systems with input saturation WANG Yongchao1, ZHANG Shengxiu1, HU Xiaoxiang1, CAO Lijia1, SUN Weichao2 (1.Dept. of Control Engineering, Rocket Force Engineering University, Xi’an 710025, China;2.Research Institute of Intelligent Control and Systems, Harbin Institute of Technology, Harbin 150001, China) The tracking problem of the nonlinear system with input saturation is investigated by using a backstepping approach based on fuzzy state observer, where the underline system contains immeasurable states and unknown control directions. Firstly, a fuzzy state observer is designed to estimate the immeasurable states. Then, the Hyperbolic tangent function with smooth property and a Nussbaum function are used to handle the input saturation. The bound of the output tracking error is set by the prescribed performance methodology. A robust controller is designed combining the backstepping approach and the dynamic surface method. The Lyapunov theory is applied to analyze the stability of the system. It is proved that all the signals of the resulting closed-loop system are semi-globally uniformly ultimately bounded(SGUUB). Finally, the longitudinal dynamics as the simulation model is given to show the effectiveness of the proposed control approach. prescribed performance;fuzzy state observer;input saturation;backstepping approach;hypersonic vehicle 10.11918/j.issn.0367-6234.2016.10.016 2015-04-14 國家自然科學基金(61304001,61304239) 王永超(1991—),男,博士研究生; 張勝修(1963—),男,教授,博士生導師 張勝修,zsx1963@aliyun.com TP273.2 A 0367-6234(2016)10-0110-09







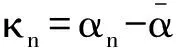
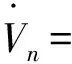
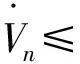
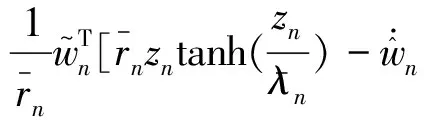
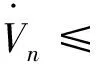


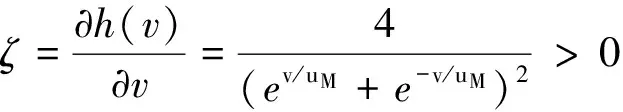
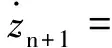


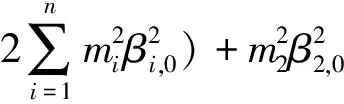

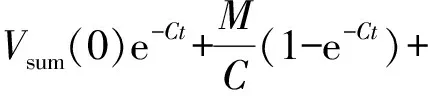
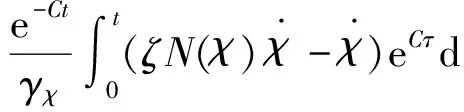
5 仿真分析

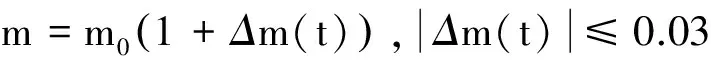



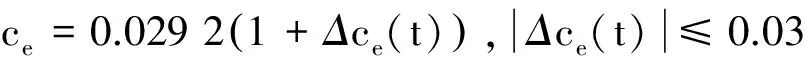
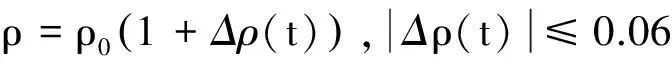
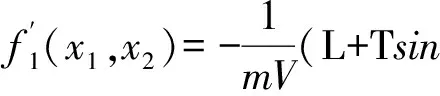

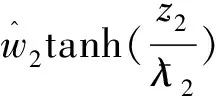
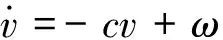

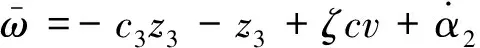
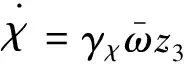

6 結 論

