重力異常物性正則化反演研究

周宇軒， 雷 宛

(成都理工大學 地球物理學院，成都 610059)

?

重力異常物性正則化反演研究

周宇軒， 雷 宛

(成都理工大學 地球物理學院，成都 610059)

經典位場物性反演是建立在數與模型之間的線性關系，利用離散正演公式將每個剖分單元相對觀測點的核函數進行計算，以尋求觀測數據與核函數有最好的相關性。該類方法在計算過程最大的問題就是在解巨大超定方程組時，導致求解極不穩定。在前人的研究基礎上，提出一種基于先驗密度模型約束正則化條件下的重力異常視密度求解方法，通過L曲線法選取最佳的參數，使求解過程中有較高的穩定性和求解精度。這里以一理論模型作為觀測數據，并引入噪聲作為觀測誤差，通過算法的對比表明，該方法有很高的計算精度和穩定性，對于需要求解大型超定矩陣的三維模型，在給定先驗初始模型的條件下，該方法仍然能夠取得很好的效果。

重力異常； 視密度； 正則化； 先驗模型； 約束反演

0 引言

重力勘探是地球物理勘探的主要分支之一。目前國內主要通過地面測量來獲取研究區各點重力場觀測值，再通過必要地改正得到重力異常值[1]。重力勘探方法作為重要的勘探手段，已經廣泛應用于油氣勘探、金屬礦勘查、地質填圖及工程與環境地球物理勘探等領域。隨著儀器、計算機、導航定位等技術的不斷發展，重力探測技術應用已經擴展到衛星、航空、海洋等方面。相應地，針對衛星、航空、海洋重力實際資料大面積、大數據量以及快速估算解釋的要求[2]，三維正反演也逐漸地發展起來。

反演是重力資料定量解釋中的重要環節之一[3]。與其他地球物理方法一樣，重力資料解釋的目的在于通過地面或航空等實測數據利用某種手段推算出地下的密度分布規律，從而達到尋找目標地質體、推斷地質體埋深和地質體分布范圍的目的。雖然能很容易找到滿足數據擬合空間的解模型，但是由于重力場的體積效應、有限觀測數據的不準確性及反演問題的欠定性等幾種因素的存在，反演結果往往產生多解性，從而很難得到一個符合實際情況的解。這就需要在反演過程中添加一些約束條件及先驗信息，最大限度地保證反演結果的正確性，如王薇等[4]提出的地震波形反演的稀疏約束正則化方法；舒夢埕等[5]提出儲層重力密度反演后驗約束正則化方法等；Tikhonov[6-7]正則化算法使反演結果更加可靠。對于反演模型可用場源目標體的形狀或遍歷地下半空間的物性值大小來表示，這就產生了兩種完全不同的反演方法：①幾何反演；②物性反演。幾何反演是在地下半空間場源體給定物性參數大小的基礎上，利用地面觀測異常來擬合幾何體(如多邊形或多面體)形狀大小，通過幾何體的形狀大小來模擬目標體的分布規律。物性反演是將觀測區域地下半空間離散化成規則的網格單元，通過反演方法確定各離散單元的物性值，由物性的分布確定場源的實際分布情況。早期以形態反演為主，主要應用于沉積基底界面反演以及形態簡單的場源體反演等。隨著計算機計算能力地提高，物性反演后來居上且從二維發展為三維，逐漸成為國內、外重力反演的主要方向[8]。

1 密度模型正演原理

建立如圖1所示的二維密度模型和觀測系統，在地表(z=0)處觀測和接收數據，d(i)為在地面第i個觀測點所得的數據，mj為地下介質剖分后第j個 單元的密度(通常是未知的)。

圖1 密度模型及觀測系統示意圖Fig.1 Schematic diagram of density model and observation system

根據圖1的重力觀測模式，d(i)與mj的定量關系如式(1)所示。

d(1)=f1,1m1+f1,2m2+f1,3m3…+f1,mmm

(1)

其中：f1,j為重力場觀測網格化后物理的距離函數。

剖分矩形截面重力正演公式，如式(2)所示。

(2)

其中：dx、dy分別為地下網格的長度和寬度；xk,zk為地下觀測點坐標；G表示牛頓萬有引力常數。

為了與實際重力異常相結合，此處計算的是每一個場源的引力在鉛垂方向上的投影，最后將它們相加。需要計算一條測線上面的重力異常值，可以用式(3)的矩陣表示。

(3)

式(3)可以化簡為式(4)：

F m=d

(4)

其中：F為表示表示觀測點與場源的核函數；m為每個網格單元的密度值；d為測線上面的重力異常觀測值。

圖2 三維密度模型和觀測系統Fig.2 3D density model and observation system

三維模型通常將地下的地質體劃分為多個立方單元體，密度模型和觀測系統如圖2所示。剖分立方體正演公式,如式(5)所示。

Δg= -G m|||[ξ ln(η+ρ)+

(5)

其中：η、ζ、ξ為網格單元的x、y、z坐標值；ρ為觀測點到單元網格的距離，其表達式如式(6)所示。

(6)

若F等于式(7)所示的公式：

(7)

則可以將式(5)表示為：Δg=F m，為每個網格單元體的密度值。

2 正則化反演原理

在反演過程中，正演擬合參與運算的剖分單元數往往大于觀測數據個數，特別是實際觀測數據總是存在觀測誤差，導致反算F方程通常是一個超定矩陣，無法穩定線性的求出精確的解，為了使解更加穩定、準確，一般需要求解一個最小二乘意義下的近似解式(8)。

‖F m-d‖2→min

(8)

最小二乘本質是線性增量修正，由于修正量與解的收斂不確定性，導致求到的解會出現由穩定收斂到逐步發散的現象，為克服上述問題，作者運用Tikhonov正則化思想設計的正則化反演模型：

(9)

其中：α是正則化參數；m0為先驗的密度模型；通過L曲線法選取最佳的α參數。

為降低反演的多解性，需要加入一個先驗模型的約束。具體求解過程推導如下：

(10)

利用最小二乘原理將上訴問題轉化為正則方程，得到的結果如式(11)所示。

(GTG+α2I)m=GTd+α2Im0

(GTG+α2I)(m-m0)=GT(d-Gm0)

(11)

令m*=m-m0,d*=d-Gm0，將其代入式(11)中，則可得到式(12)。

(GTG+α2I)m*=GTd*

(12)

求解上述方程，對矩陣G進行奇異值(SVD)分解：

(VSTUTUSVT+α2I)m*=VSTUTd*

(VSTSVT+α2I)m*=VSTUTd*

假設x*=VTm*，m=Vx,VVT=I

則有：

(STS+α2I)x*=STUTd*

(13)

從而可求到：

(14)

令m-m0=m*=Vx*,d=d*+Gm0，代入式(14)，可以得到：

(15)

其中：S、U、V由矩陣G的SVD分解得到；Gm0、m0都是已知量，因此，作者采用L-curve曲線方法[9](圖3)求解。

圖3 L-curve曲線Fig.3 L-curve curve

正則化參數α的取值規則是從小取到大，依次用不同α算出的‖G m-d‖、‖m-m0‖取對數顯示成L曲線。通過L曲線可以看出，當α很小時‖G m-d‖的值較小，而‖m-m0‖較大，這說明取較小的α時數據擬合效果較好，但反演結果與初始后驗模型相比擾動較大。當α取較大時擬合誤差‖G m-d‖變大，而反演結果與后驗模型的距離‖m-m0‖變小。因此選擇L曲線曲率最大處作為最優有α參數，這樣既能平衡擬合誤差，又能兼顧后驗模型[10-12]。

求出α以后，代入到公式(15)中，即可求出m。

3 數值試驗

設計一個二維模型(圖4)，其參數設置為：中間方形的密度為ρ=2 g/cm3，旁側的密度設為 g/cm3；長寬分別為300 m、300 m，中心埋深為500 m；數據網格為10 m×20 m，測線上的數據點采樣為2 000個，計算重力正演異常(圖5)。

為模擬觀測數據的隨機觀測誤差，對該重力異常進行隨機噪聲添加(圖6)。

對圖6所得重力異常數據進行最小二乘優化反演，得到結果如圖7所示，反演的視密度比較接近真實值2，但從視密度成像幾何分布特征來看，與設計理論模型圖4存在很明顯的差異。在給定先驗密度模型約束條件下，采用正則化方法，對含噪聲重力異常數據進行反演，其視密度成像結果如圖8所示。從圖8中可以看出,無論密度反演值還是密度分布成像特征，均較最小二乘法有很好的改進，與設計模型(圖4)有很好的對比性，表明基于正則化條件下的視密度反演算法，在噪聲條件下，反演解未陷于局部收斂，其解有很高的穩定性和求解精度。

圖5 正演重力異常Fig.5 Positive gravity anomaly

圖6 加噪音正演重力異常Fig.6 Positive gravity anomaly with noise

將上述算法推廣到三維模型，設計如圖9的模型，其中模型密度為ρ=2 g/cm3，圍巖密度為ρ=0.4 g/cm3；長、寬、高分別為300 m、300 m、300 m，中心埋深為500 m；數據網格為10 m×10 m×10 m，數據節點為1 000個；觀測面數據采樣為50×50=2 500個；其正演重力異常見圖10。 設置如圖11所示的先驗初始模型，采用該先驗模型進行正則化條件下的重力異常數據三維物性反演，得到的結果如圖12所示。從圖12中可以看出，反演的視密度大小及幾何形狀分布與圖9有很高的吻合度。對比二維和三維反演的計算效率(表1)。

由表1可以看出，三維正則化物性反演雖然在迭代時間上消耗較多，但迭代次數相對二維反演較小，且能達到同等的效果。表明該方法在三維大型數據運算中仍具有很高的求解精度和穩定的求算解。

圖7 最小二乘算法反演結果Fig.7 Least square algorithm inversion results

圖8 加噪音正則化算法反演結果Fig.8 Inversion results with noise

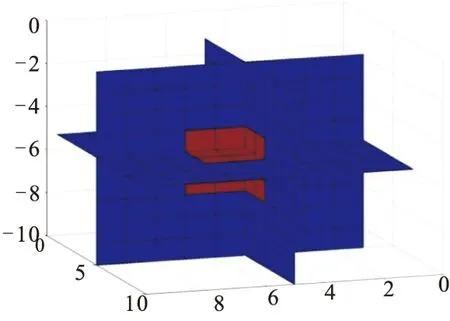
圖9 三維正演模型Fig.9 3D forward modeling

圖10 三維正演平面圖Fig.10 3D positive results plan

圖11 先驗初始模型Fig.11 A priori initial model

圖12 反演結果Fig.12 Inversion results

網格點數迭代次數時間消耗二維反演10*20150.34三維正則化反演10*10*10100.53

4 結論

1)重力異常物性反演在解巨大超定方程組時，導致求解極不穩定，作者提出基于正則化條件下的約束反演，對于解決這類問題有很好的效果。

2)二維噪聲模型和三維密度模型數值模擬結果表明，基于正則化條件下的反演算法，特別是在給定先驗初始密度模型約束條件下，在求解的精度和求解的穩定性有其相對優勢。

[1] GROETSCH C W. Inverse Problems[M]. Washington: The Mathematical Association of America, 1999.

[2] 陳召曦,孟小紅,郭良輝.重磁數據三維物性反演方法進展[J].地球物理學進展,2012,27(12)：503-511.

CHEN Z X, MENG X H, GUO L H. Review of 3D property inversion of gravity and magneticdata[J]. 2012,27(12)：503-511.(In Chinese)

[3] 陳桂廷,羅強,周宇軒,等.三維位場正則化向下延拓成像技術[J].科技創新導報,2014(26):46-47.

CHEN G T, LUO Q, ZHOU Y X ,et al.Down-ward extension imaging techn ique of threedimensional potential field[J]. Scienc Science and Technology Innovation Herald,2014(26):46-47. (In Chinese)

[4] 肖庭延. 反問題的數值解法[M]. 北京：科學出版社, 2003.

XIAO T Y.Numerical solution of the inverse problem[M].Beijing:Science Press, 2003. (In Chinese)

[5] 舒夢埕,王彥飛.儲層重力密度反演后驗約束正則化方法[J].地球物理學,2015,58(6):2079-2086.SHU M C,WANG Y F.The posterior constrained regularization method for reservoirdensity inversion[J].ActaGeophysicaSinica,2015,58(6):2079-2086.(In Chinese)

[6] 徐新禹，李建成，王正濤,等.Tiknohov正則化方法在GOCE重力場中的模擬研究[J].測繪學報，2010,39(5)：466-470.

XU X Y, LI J C, WANG Z T, et al.The simulation research on the Tikhonov regularization applied in Gravity Field[J].Acta Geodaeticaet Cartograph-icaSinica, 2010,39(5)：466-470. (In Chinese)

[7] 傅初黎，洪芳，向團.不適定問題的Tikhonov正則化方法[J].計算數學,2006,28(3):237-246.

FU C L,HONG F,XIANG T.Iterated Tikhonov regularization for ill-poseproblems[J].Mathematica Numerica Sinica,2006,28(3)：237-246.(In Chinese)

[8] 王邦華,王理.重磁位場的正則化向下延拓[J].物探化探計算技術,1998,20(1):30-35.

WANG B H. WANG L.A new normalized thod of down ward extrapolation for potential field[J]. Computing Techniques for Geophysical and Geochemical Exploration,1998,20(1):30-35. (In Chinese)

[9] TVEITO A, LANGTANGEN H P, NIELSEN B F,et al. Parameter estimation and Inverse problems[M].Pittsburgh:Academix Press,2013.

[10]馮寶賓. 不適定問題的正則化解算方法設計及應用[D]. 成都：成都理工大學, 2010.

FENG B B.Design and application of theregularization method for solving ill posed problems[D].Chengdu：Chengdu University of Technology,2010.(In Chinese)

[11]ARSENIN, IA. V. Solutions of ill-posed problems [M]. Washington:Winston,1977.

[12]劉銀萍,王祝文,杜曉娟,等. 基于Tikhonov正則化算法的重力數據三維約束反演[J]. 地球物理學報, 2013, 56(5):1650-1659.

LIU Y P, WANG Z W, DU X J, et al. 3D constrained inversion of gravity data based on Tikhonov regularization algorithm[J].Chinese Journal Geophysics,2013,56(5):1650-1659. (In Chinese)

Study on physical properties regularization inversion of gravity anomaly

ZHOU Yu-xuan， LEI Wan

(College of Geophysics,Chengdu University of Technology,Chengdu 610059，China)

Classical potential field physical properties inversion is based on the linear relationship between the number and the model.We calculate each cross-sectional unit relative to observation point kernel function by using discrete forward formula to seek the best correlation in the observational data and the kernel function. The biggest problem of this kind of method calculation is unstable system to solving when we solve the large set of equations. On the basis of previous research,a kind of density algorithm is put forward based on the prior density model regularization constraint conditions of gravity anomaly in this study.The solution process has high stability and accuracy by using the L-curve method to select optimal parameters. In this paper,we establish a theoretical model as the observation data and introduce a noise as the observation error.Calculation results show that the method has high accuracy and stability through the comparison of different algorithms.Given a priori model of the initial conditions,the method can still achieve good results for the need for solving large over determined matrix of 3D model.

gravity anomaly; apparent density; regularization; a priori model; constrained inversion

2016-04-13 改回日期：2016-06-14

中國地質調查項目(12130113095100)

周宇軒(1992-),男，碩士，從事地球物理勘探方法研究，E-mail:zhouyuxuan@163.com。

1001-1749(2016)05-0579-05

P 631.1

A

10.3969/j.issn.1001-1749.2016.05.01