投影尋蹤模型在行蓄洪區運用風險評價中的應用

黃健元,金廣宇,于彥博

(1.河海大學公共管理學院,江蘇 南京 210098; 2.淮河水利委員會水利水電工程技術研究中心,安徽 蚌埠 233001)

?

投影尋蹤模型在行蓄洪區運用風險評價中的應用

黃健元1,金廣宇1,于彥博2

(1.河海大學公共管理學院,江蘇 南京 210098; 2.淮河水利委員會水利水電工程技術研究中心,安徽 蚌埠 233001)

將行蓄洪區運用風險評價指標體系應用于基于信息熵的投影尋蹤模型,得到風險評價投影值。根據結果把淮河干流行蓄洪區運用風險等級分為4類,風險等級及分類區間從高到低依次為Ⅰ級,投影值≥4.16,包括4個蓄洪區和壽西湖、鮑集圩2個行洪區;Ⅱ級,投影值為4.10～4.16,包括湯漁湖等4個行洪區;Ⅲ級,投影值為3.90～4.16,包括香浮段等7個行洪區;Ⅳ級,投影值為0～3.90,包括邱家湖等4個行洪區。

信息熵;投影尋蹤模型;風險等級;行蓄洪區

行蓄洪區運用風險評價是實際運用決策中的基礎工作。一直以來,對行蓄洪區運用風險的研究方法各不相同,李紹飛等[1]建立了以致災因子、孕災環境、承載體屬性三方面為基礎的蓄滯洪區洪災風險評價指標體系,并制定了洪災風險等級評價標準。包君等[2-3]根據行蓄洪區的運用風險特征,從社會風險、經濟風險、行洪危險和承災能力等4個方面,構建了包括16項指標的行蓄洪區運用風險綜合評價指標體系,分別利用模糊ISODATA聚類分析法和基于模糊優選模型、決策優選方法的混合模型對淮河流域21個行蓄洪區的運用風險進行評價,將淮河干流行蓄洪區從高到低分為5個風險等級。

與以往研究不同,考慮到風險評價指標在一定程度上存在著相關性,本文利用基于信息熵的投影尋蹤模型對行蓄洪區運用風險進行評價,得到有關行蓄洪區運用風險的相對水平值,并劃分淮河干流21個行蓄洪區的運用風險等級。混合模型是對典型行蓄洪區運用風險進行綜合評價,對比分析各相關行蓄洪區運用時的風險因素;模糊ISODATA聚類分析法是對調研獲取的數據對應的風險進行聚類分析,將行蓄洪區運用風險分類管理;而基于信息熵的行蓄洪區運用風險評價投影尋蹤模型是得到有關行蓄洪區運用風險的相對水平值。上述3種評價方法在發揮各自價值的同時,可以相互校驗,使得評價結果更為合理。

1 行蓄洪區運用風險評價指標體系與評價指標值采集

包君等[2-3]分別利用模糊ISODATA聚類分析法和基于模糊優選模型、決策優選方法的混合模型對淮河干流行蓄洪區運用風險進行聚類、排序分析,而本文利用投影尋蹤模型對淮河干流行蓄洪區運用風險進行相對水平值計算。為了更好地比較,故直接采用已有行蓄洪區運用風險綜合評價指標體系(見表1)[2]，評價指標值也直接采用已有相關指標數據[2]。

2 投影尋蹤模型

傳統的統計評價方法只適用于2個或者3個評價對象等較少指標的綜合評價,而投影尋蹤法因其具有適用范圍廣、靈活簡單等優點,在風險評價中始終占據著重要位置,適用于多指標、多個評價對象、復雜化的風險評價。行蓄洪區風險評價指標體系中含有多個指標,并且作為評價對象的行蓄洪區也有多個,因此,運用投影尋蹤方法評價行蓄洪區的運用風險顯然是合適的。

投影尋蹤聚類技術[4]實質上是一種將高維數據投影到低維子空間上的降維處理技術,即將影響問題的多因素指標通過投影尋蹤聚類分析,得到反映其綜合指標特性的投影特征值,進而建立投影特征值與因變量的一一對應關系函數。通過優化投影指標函數,求出能反映原高維數據結構和特征的投影向量,分析低維數據來達到研究和分析高維數據的目的。

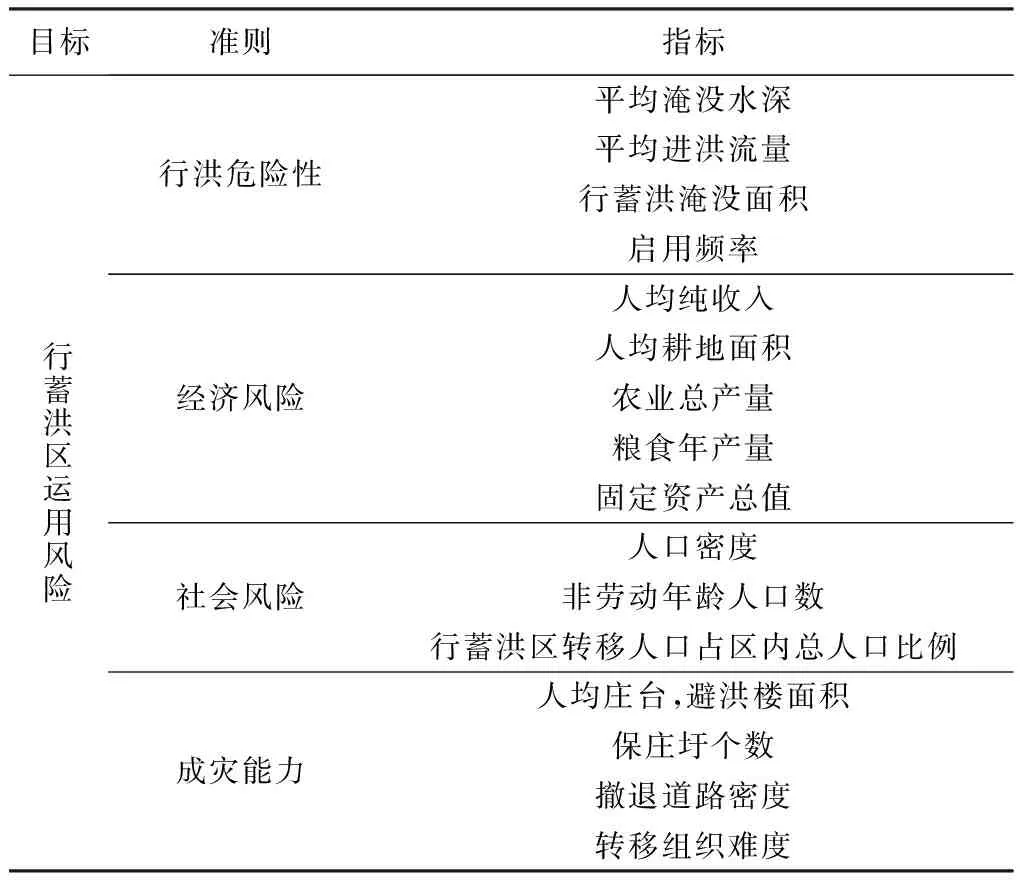
表1 行蓄洪區運用風險評價指標體系

2.1 指標值的無量綱化處理

假設第i個樣本的第j個指標為x*(i,j)(i=1,2,…,n;j=1,2,…,p),其中n,p分別為樣本的個數和指標的數目。為消除各指標的量綱和統一各指標值的變化范圍,可利用極值歸一化處理法。

對于越大越優的指標:

(1)

對于越小越優的指標:

(2)

式中:xmax(j)和xmin(j)分別為第j個指標值的最大值和最小值;x(i,j)為指標特征值歸一化的序列。

轉移組織難度指標運用模糊一致矩陣[5]進行量化處理并利用映射

將優度值si(i=1,2,…,21)轉化為在[0,1]中取值的優屬度ri。優屬度越高行蓄洪區運用風險越高。計算結果見表2。

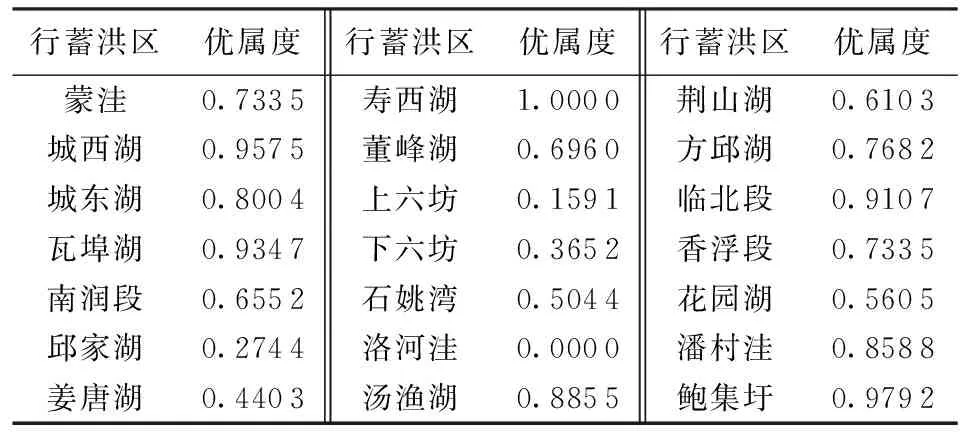
表2 轉移組織難度優屬度

2.2 線性投影

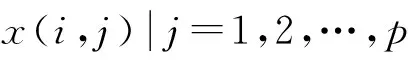
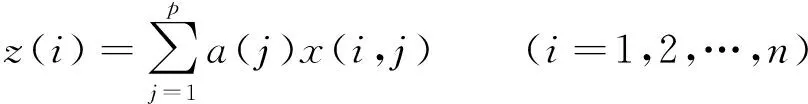
(3)

根據z(i)的一維散布圖可進行分類,其中a為單位長度向量。投影向量的大小實際上反映了各評價指標對評價等級的影響程度。根據Jaynes[6]最大熵原理,在只能掌握部分信息的情況下要對概率分布做出推斷,應取滿足約束條件同時使信息熵值最大的概率分布,熵值越大意味著人為添加的約束和假設越少。因此,可構造最大熵目標函數如下:

(4)

(5)

式中:Sa為z(i)的標準差;Da為z(i)的局部密度。即:

(6)

(7)

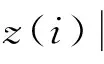
2.3 投影函數最優化

當各指標值的樣本集給定時,Q(a)只隨投影方向a的變化而變化。不同的投影方向反映不同的數據結構特征,而最佳的投影方向就是最大可能暴露高維數據某類特征結構的投影方向。因此可以通過求解投影指標函數最大化問題來估計最佳投影方向。

最大化目標函數:

maxQ(a)=H(a)SaDa

(8)

約束條件:

(9)

這是一個復雜的非線性最優化問題,此處運用粒子群優化算法來求解這一尋優問題。

2.3.1 粒子群優化算法原理

粒子群算法(PSO)處理優化問題時,類似于在D維空間中搜索以一定質量飛行的粒子。空間中的各個粒子都有各自的位置和飛行速度,各個粒子都了解自己到目前為止搜索到的最好位置和整個群體內部其他粒子的歷時最好點,看作粒子同伴的經驗。各個粒子都隨著最優粒子進行搜索。如果獲得較好的解,則以較好的解為起始依據尋找下一個解[8]。

2.3.2 粒子群優化算法建立過程

隨機為m個粒子產生初始速度和初始位置后,假設D維搜索空間中第i個粒子的位置為:Xi=(xi1,xi2,…,xiD),速度為:Vi=(vi1,vi2,…,viD)(1≤i≤m)。迭代過程中,第i個粒子經歷的最好點記為Pi=(pi1,pi2,…,piD);整個粒子群所經過的最好點記為Pg=(pg1,pg2,…,pgD)。根據跟蹤的兩個最優解粒子不斷更新自己,速度和位置變化公式如下:

(10)

(11)

式中:w為慣性系數,防止算法過早收斂;c1、c2為學習因子，通常c1=c2=2;ξ和η是定義在[0,1]區間上的偽隨機數。

該算法的一般步驟為:①粒子群初始化;②估算粒子群中粒子的適應值;③對比粒子與它所經歷最佳位置的適應值,若更好則替代原位置;④比較所有粒子所經歷最好位置的適應值,將最好的值對應的位置作為當前的全局最好位置;⑤用式(10)、式(11)更新粒子的位置和速度;⑥若未達到終止條件,則回到第②步繼續進行迭代計算。通常達到足夠好的適應值或者預先設計的最大迭代次數則終止計算。

2.4 等級評價

獲得最佳投影方向后,可求各個樣本點的投影值z*(i),根據z*(i)的值進行從大到小排序或對各個樣本點進行分類。

3 基于投影尋蹤模型的行蓄洪區運用風險評價結果分析

借助MATLAB仿真,利用投影尋蹤模型對行蓄洪區運用風險進行評價。選取不同的迭代次數和迭代步長求解投影函數的最大值。其中,粒子群中粒子數為21,最大迭代次數為100。部分計算結果見表3。

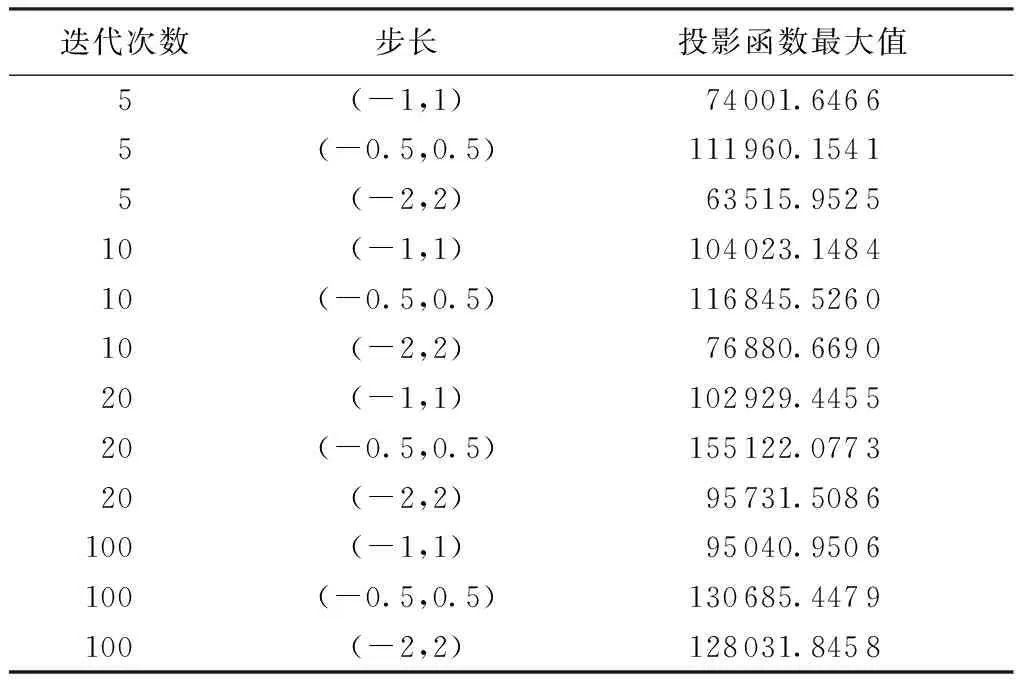
表3 不同迭代次數和步長下的投影函數最大值

從表3的計算結果中發現投影函數的最大值為155 122.0773。因此最佳投影方向為(0.157 2,-0.770 6,0.349 6,0.838 3,-0.350 7,0.801 1,0.138 4,0.200 9,0.608 3,-0.172 0,-0.349 5,0.104 5,0.833 6,0.600 3,0.809 1,0.510 0),將最佳投影方向代入模型中,計算樣本數據的投影值,計算結果見表4。

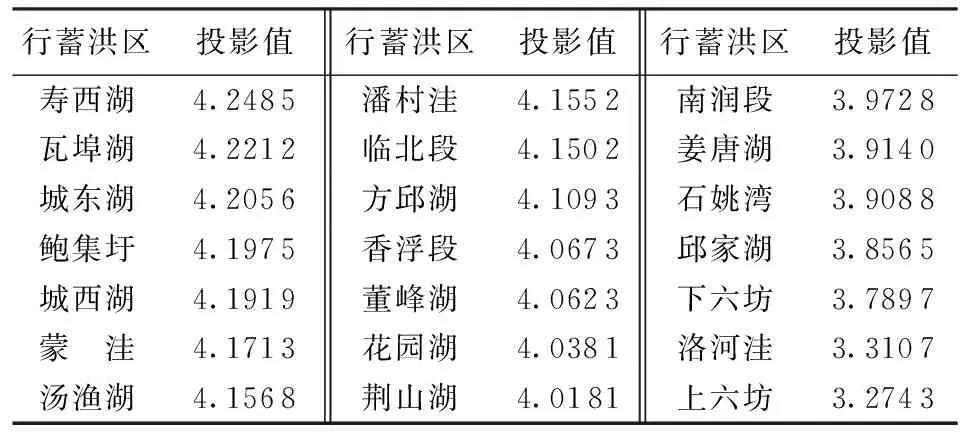
表4 淮河干流行蓄洪區運用風險評價投影值

為了方便把投影尋蹤模型與模糊ISODATA方法和混合模型進行比較,根據表4中的投影值大小可將行蓄洪區的運用風險分為4類,風險等級及分類區間從高到低依次為Ⅰ級(投影值≥4.16),Ⅱ級(投影值為4.10～4.16),Ⅲ級(投影值為3.90～4.16),Ⅳ級(投影值為0～3.90)。不同的風險等級代表啟用該類行蓄洪區時會帶來不同程度的經濟風險和社會風險,造成不同程度的洪災損失(包括直接損失和間接損失)。如Ⅰ級行蓄洪區指啟用該類行蓄洪區行蓄洪時帶來的經濟風險和社會風險最大,造成的損失最高。對應的Ⅳ級行蓄洪區啟用時洪水淹沒造成的損失最小。

結合淮河干流行蓄洪區實際情況對21個行蓄洪區運用風險進行分級,其等級具體劃分結果見表5。

根據結果可知:4個蓄洪區中,城西湖是淮河中游蓄洪量最大的蓄洪區,蓄洪量達29.5 億m3,被譽為淮河防汛的最后一張王牌。瓦埠湖蓄洪區是淮河中游面積最大的蓄洪區,耕地面積廣闊。2020年瓦埠湖規劃人口40.77萬人,蓄洪時轉移人口多。蒙洼和城東湖糧食年產量分別為8.52萬t和10.97萬t,因此4個蓄洪區在運用時都具有Ⅰ級風險。可見蓄洪區都有高的運用風險。

表5 淮河干流行蓄洪區運用風險等級劃分結果

行洪區中的鮑集圩、壽西湖兩個行洪區因經濟水平相對較高、固定資產總值高、行蓄洪時人口轉移比例大、人均避洪設施面積小等因素導致其運用風險為Ⅰ級風險。邱家湖和下六坊因經濟水平相對落后、人均安全設施面積大、撤退時轉移人口比例小等因素綜合作用而使運用風險等級為Ⅳ級風險。上六坊和洛河洼在運用時無須轉移人口,行洪阻力較小,因此,運用風險等級為Ⅳ級風險。湯漁湖、潘村洼和臨北段3個行洪區因經濟水平相對較高、固定資產總值較高、行蓄洪時人口轉移比例較大、人均避洪設施面積小等因素導致其運用風險為Ⅱ級風險。方邱湖農業總產值和固定資產總值較高,因此其運用風險為Ⅱ級風險。其他行洪區運用風險略低于方邱湖,處于Ⅲ級風險水平。因此,在啟用行蓄洪區時,應優先考慮風險等級較低的行洪區,再考慮啟用蓄洪區。

4 結 論

a. 通過比較3種模型結果分析發現:淮河干流4個蓄洪區的運用風險都較高,處于高或較高水平。行洪區中壽西湖、鮑集圩等處于高風險水平,洛河洼、上六坊堤、下六坊堤等運用風險處于較低或低水平。不論從3種模型的對比來看,還是參照歷年運用情況和調整規劃方案,都說明評價結果具有一定的合理性。基于指標體系和相關指標值,利用基于信息熵的行蓄洪區運用風險評價投影尋蹤模型,得到有關行蓄洪區運用風險的相對水平值,對行蓄洪區的運用風險從高到低進行等級劃分是行蓄洪區運用風險評價方法選擇的又一嘗試,并且可以通過投影尋蹤模型、混合模型和模糊ISODATA聚類分析法三者相互校驗,使得評價結果更為合理。行蓄洪區運用風險評價投影尋蹤模型的建立,旨在引進一種新的行蓄洪區運用風險評價方法,是對已有評價方法的有益補充。

b. 運用投影尋蹤模型對淮河干流行蓄洪區的運用風險進行評價分析,結果如下:4個蓄洪區在運用時全具有Ⅰ級風險,風險等級高,壽西湖、鮑集圩兩個行洪區也屬于Ⅰ級風險;湯漁湖、潘村洼、臨北段、方邱湖4個行洪區屬于Ⅱ級風險,風險等級較高;邱家湖、下六坊、上六坊、洛河洼4個行洪區屬于Ⅳ級風險,風險等級低;其余7個行洪區屬于Ⅲ級風險,風險等級較低。

c. 本研究仍存在不足之處:首先,各指標之間存在一定程度的相關性。其次,利用投影尋蹤模型的計算量較大,并且將高維數據投影到低維子空間上,必然造成一些原始信息的損失。因此,在對高維數據進行降維的過程中,如何保持原數據信息的完整性,是需要進一步研究解決的問題。

[1] 李紹飛,于萍,孫書洪. 基于神經網絡的蓄滯洪區洪災風險模糊綜合評價[J]. 中國農村水利水電,2008(6):60-64.

[2] 包君,黃健元. 基于改進ISODATA的行蓄洪區運用風險評價[J]. 人民黃河,2014,36(7):41-44.

[3] 包君,王再明. 混合模型在行蓄洪區運用風險評價中的應用[J]. 中國農村水利水電,2015(3):95-97.

[4] 王兆禮,賴成光,陳曉宏. 基于熵權的洪災風險空間模糊綜合評價模型[J]. 水力發電學報,2012,31(5):35-40.

[5] 劉群昌,許迪,謝崇寶,等. 波涌灌溉技術田間適應性分析[J]. 農業工程學報,2002,18(1):35-40.

[6] JAYNES E T. Information theory and statistical mechanics[J]. Physical Review,1957,106:620-630.

[7] 霍映寶,韓之俊. 基于廣義最大熵原理和遺傳算法的多指標權重確定方法研究[J]. 數理統計與管理，2005,24(3):40-42.

[8] 張雙虎,黃強,吳洪濤,等. 水電站水庫優化調度的改進粒子群算法[J]. 水力發電學報，2007,26(1):2-4.

水利部公益性行業科研專項經費項目(201301065)

黃健元(1964—),男,江蘇溧陽人,教授,主要從事公共管理、統計學等研究。E-mail:hjy1964@sina.com

10.3880/j.issn.1003-9511.2016.05.014

P426

A

1003-9511(2016)05-0060-04

2016-04-23 編輯：胡新宇)