馬氏體不銹鋼的微觀組織各向異性對微區應力和氫分布的影響

鐘振前,田志凌，楊 春，2

(1 鋼鐵研究總院 分析測試所，北京 100081；2 清華大學 材料學院，北京 100083)

?

馬氏體不銹鋼的微觀組織各向異性對微區應力和氫分布的影響

鐘振前1,田志凌1，楊 春1，2

(1 鋼鐵研究總院 分析測試所，北京 100081；2 清華大學 材料學院，北京 100083)

利用電子背散射衍射(EBSD)實驗分析了馬氏體組織的微區彈性剛度分布，并在此基礎上建立應力-氫交互作用的耦合有限元模型，研究馬氏體組織的各向異性對微區應力和氫分布的影響。結果表明: 相鄰Block板條束之間的取向差互成60°，在同一受力方向上不同Block板條束具有不同的彈性剛度，從而引發組織間的微區應力和氫呈不均勻分布，Block板條束是表征微區應力的組織單元。Block板條束彈性剛度梯度和組織尺寸決定了組織間的應力集中，而應力集中又影響了氫的分布。彈性剛度梯度高和板條束尺寸大的Block組織單元應力集中較為嚴重，并富集高濃度的氫，最終引發氫致開裂。上述模擬結果與氫脆斷口的微觀斷裂形貌和氫脆裂紋的EBSD分析結果相符。

各向異性；氫擴散；彈性剛度；氫脆；FEM；EBSD

氫致延遲斷裂是高強結構鋼斷裂失效的常見形式之一，應力、氫、材料三者的交互作用是氫致延遲斷裂發生的主要原因。其中應力扮演了極其重要的角色，這是因為應力可以極大地提高氫在材料中的擴散能力，并使部分氫脫離氫陷阱的束縛[1]，驅動氫向應力集中處擴散和聚集[2]，最終萌生氫致延遲裂紋。

目前，應力對氫的擴散[3,4]和聚集[5,6]作用的研究更多集中在宏觀尺度上，例如在加載應力條件下用電化學滲透方法研究氫的擴散行為，或通過預制缺口拉伸試樣的方式計算缺口處的應力集中系數和氫的聚集濃度[7]。少量微觀尺度上的氫擴散研究主要集中在氫與位錯[8]或缺陷[9,10]的相互作用，以及氫對局部[11,12]塑性變形的影響等方面上，但對應力作用下氫在馬氏體微觀組織間的分布和富集的研究鮮有報道，而開展此項研究工作對探求氫脆微觀機理和預防氫脆斷裂事故的發生具有重要意義。

由于材料微觀組織結構的各向異性，氫的微區分布是不均勻的，氫的局部濃度與多晶體材料中的微區應變相關，而微區應變由晶體彈性剛度[13,14]的各向異性決定。本工作用彈性剛度計算微區應變的方法，與氫的Fick擴散定律結合起來，分析應力作用下氫在馬氏體微觀組織間的微區分布。該研究方法可概括為3個步驟：(1)通過電子背散射衍射(Electron Back Scatter Diffraction,EBSD)測定材料的微區彈性剛度[15,16]分布；(2)利用軟件Abaqus開發微觀組織的數值模型計算微區應力；(3)根據應力對氫擴散的驅動作用，分析氫的局部聚集行為。

1 實驗材料與方法

1.1 慢拉伸實驗

實驗材料選用0Cr16Ni5Mo，其化學成分(質量分數/%)為：C 0.04，Si 0.39，Mn 0.78，P 0.027，S 0.012，Cr 15.81，Ni 5.25，Mo 1.05。經淬火(980℃×2h)+高溫回火(500℃×4 h)調質熱處理。

慢拉伸實驗分別在快速滲氫溶液和大氣中進行。制取兩根板狀拉伸試樣(厚度2mm，寬度4mm，標距為30mm)，表面粗糙度為Ra=3.2μm。將其中一根試樣的中間部分浸入到快速滲氫液(0.5mol/L H2SO4+少量 As2O3)中，兩端夾持區固定在WDML-1型微機控制慢應變速率力學試驗機上。在200mA/cm2的電流下預充氫4h后，以0.003mm/min的速率進行慢拉伸實驗(充氫不停止)。另取一根同規格的試樣在大氣中以同樣的加載速率進行慢拉伸實驗。將拉斷后的兩試樣置于SEM下(JSM-6400)觀察并比較斷口的微觀形貌。

1.2 EBSD實驗及微區彈性剛度分析

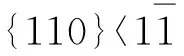
2 有限元分析

2.1 力學模型

根據微觀組織(見圖1(a))形態和尺寸建立材料微區結構的有限元模型，模擬結構如圖1(b)所示，以1.5μm為單元尺寸進行網格劃分，共得到4519個單元(如圖1(c)所示)。

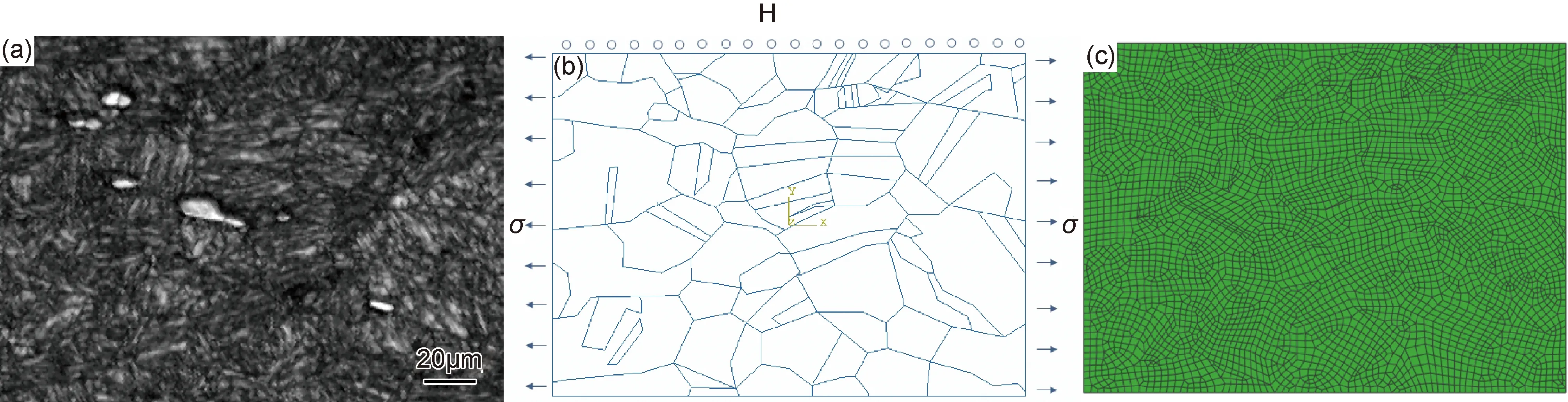
圖1 馬氏體組織微區結構模型及邊界條件(a)板條馬氏體微觀組織結構；(b)在微觀組織結構基礎上建立模型；(c)網格劃分Fig.1 Martensite microstructure model and boundary conditions(a) microstructure of lathmartensite;(b)numerical model based on microstructure;(c)mesh of model

2.2 氫濃度模型

由于高強結構鋼中位錯運動對氫運輸的貢獻很小[18]，因此忽略結構缺陷對氫的陷阱作用[7]，假定氫的擴散富集只由應力驅動控制，應力對氫的擴散驅動遵循下列公式：

(1)

(2)

根據傳質理論：

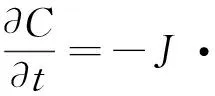
(3)

將公式(1)，(2)代入(3)，得出應力與氫濃度的關系公式：

(4)

力學計算完成后，將單位類型轉換DCAX4，將應力代入公式(4)即可得出氫濃度。

2.3 材料參數及邊界條件設定

各節點的初始氫濃度C0設置為1×10-6，上邊界氫濃度C設置為4×10-6，如圖1(b)所示。材料密度取7850kg/m3，泊松比取0.3。在模型的橫向方向上加載均勻分布的應力，如圖1(b)中σ，并輸入各板條束的彈性剛度，其值由EBSD實驗得出，如圖2(a)所示。

3 結果與分析

3.1 馬氏體組織取向分析及彈性剛度分布

圖2(a)是材料的彈性剛度分布圖，可見Packet由許多平行的Block板條束組成，選取3個不同形狀和尺寸的Packet板條束，如圖2(a)中Packet 1，Packet 2，Packet 3，在各Packet內部分別垂直于Block板條束作一條路徑，如圖中箭頭所示路徑，分析路徑上不同組織單元的取向差、彈性剛度、Taylor因子的變化趨勢。

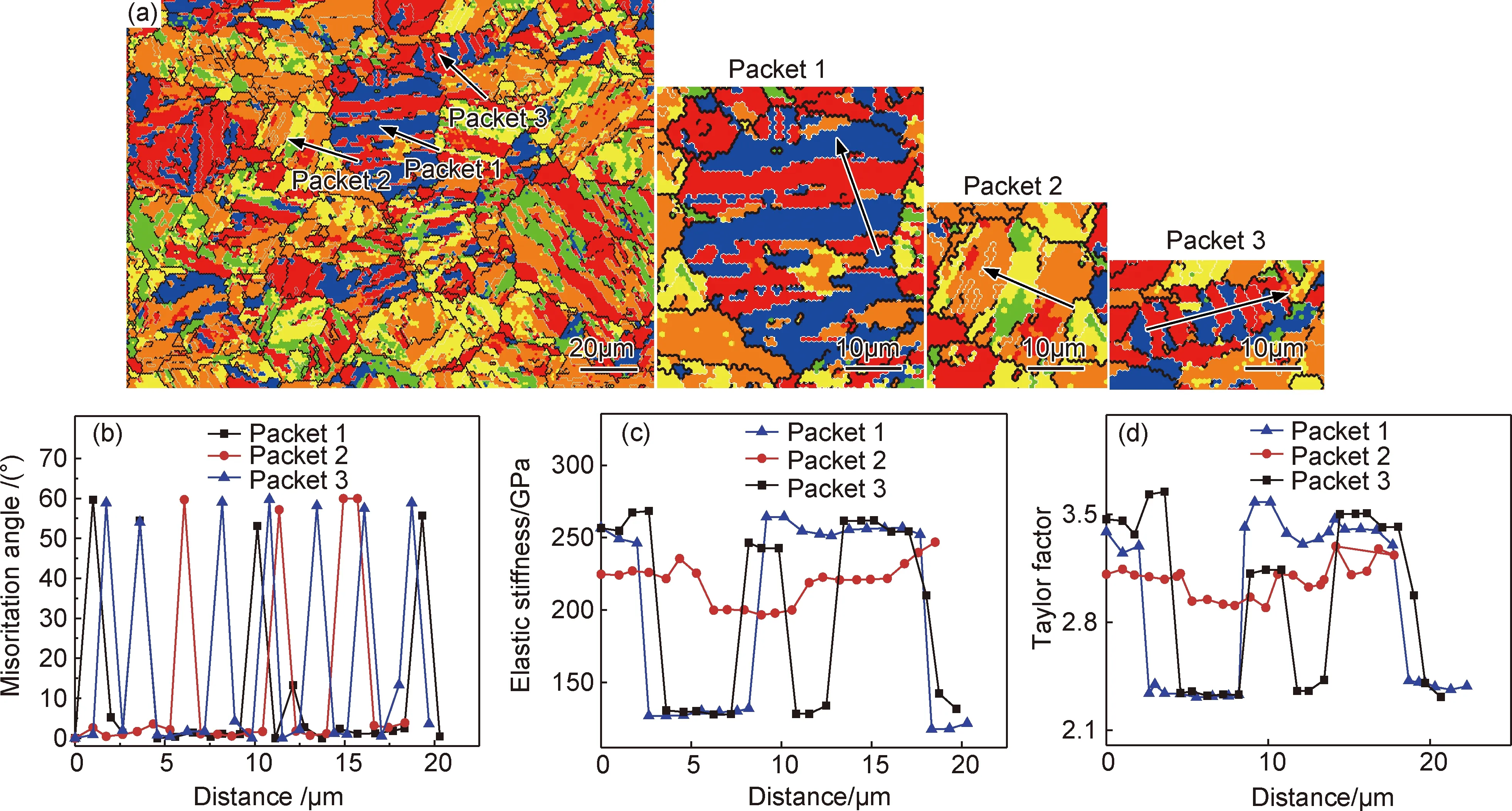
圖2 馬氏體組織的晶體取向、彈性剛度和Taylor因子 (a)彈性剛度分布圖及3個Packet板條束的內部路徑；(b)3個Packet內部路徑的點對點取向差變化；(c)3個Packet內的彈性剛度分布曲線；(d)3個Packet內的Taylor factor的分布Fig.2 Crystal orientation，elastic stiffness and Taylor factor for martensite(a) the elastic stiffness distribution along 3 Paths respectively in the 3 Packets;(b) point to point misorientation distribution along 3 paths in the 3 Packets;(c)elastic stiffness distribution in the 3 Packets;(d)Taylor factor distribution in the 3 Packets

圖2(b)中取向差分布曲線表明，3條不同路徑上的取向差的變化規律較為一致，相鄰Block板條束的取向差均為60°，同一Block板條束內的不同Lath板條取向差均基本在5°以內。

盡管3個路徑上相鄰Block板條束的取向差均為60°，但彈性模量和Taylor因子的大小沒有明顯的分布規律，如圖2(c)，(d)所示，有些相鄰板條束的彈性模量和Taylor因子相差很大(Packet 1，3內部的Block板條束)，有些相差很小(Packet 2內部的Block板條束)。這是因為彈性剛度和Taylor因子是矢量，其大小主要與晶體取向和受力方向有關，而取向差是標量，其大小與受力方向無關，只由相鄰板條束的取向關系決定。這在一定程度上表明，取向差只能表示晶界類型，并不能用來表征微區應變量。

Taylor因子可以用來表示多晶體材料中各晶體取向的胞元在某一受力方向上的變形能力，反映各胞元之間的形變約束關系和晶體滑移的優先性。彈性剛度和Taylor因子的變化曲線相近似，以及Taylor因子和彈性剛度之間的計算關系[21]表明，微區彈性剛度可以用來表征某一受力方向上的晶體滑移性能和微區應變。

3.2 彈性剛度和板條束的大小對氫濃度的影響

將EBSD得到的彈性剛度實驗數據輸入模型中，進行應力和氫濃度的模擬計算。圖3(a)為沒有外加應力時，氫從上邊界向內擴散200s后的濃度分布圖。氫濃度在X方向上呈均勻分布，在Y方向上呈梯度分布，以邊界濃度最高，向內依次逐漸降低；因此，無應力作用時，氫的濃度變化只與濃度梯度和擴散時間有關，而與板條束的彈性剛度無關。圖3(b)為外加均布載荷80MPa下的應力云圖，如σL為各Block板條束上的局部應力，σ0為邊界均布應力，定義應力集中系數α=σL/σ0，根據應力云圖可以計算各Block板條束的應力集中系數。圖3(c)為同樣加載條件下氫濃度的分布圖。對照圖3(b)，(c)可見，氫的濃度分布與應力分布規律基本一致，應力集中系數高的區域其氫濃度也較高。

在應力云圖和氫分布圖的不同Block板條束上采集計算數據，分析彈性剛度梯度(相鄰Block的彈性剛度之差)和板條束長度尺寸對氫濃度和應力集中系數的影響，如圖4(a)，(b)所示，可見隨著這些參數的增大，應力集中系數和氫濃度總體也在增加。

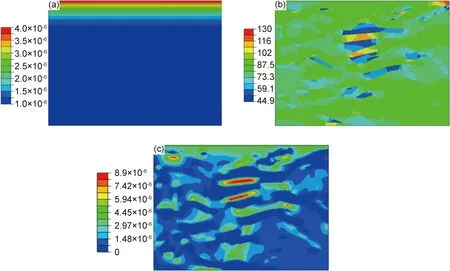
圖3 應力及氫濃度分布 (a) 無應力作用時氫的濃度分布；(b)加載80MPa時應力在組織間的分布；(c)加載80MPa時氫濃度的分布Fig.3 Distribution of stress and hydrogen concentration(a) hydrogen diffusion by hydrogen concentration gradient with no stress driving；(b) stress distribution under uniformed load of 80MPa on the boundary；(c) hydrogen concentration distribution under uniformed load of 80MPa

3.3 應力集中系數對氫濃度的影響

圖5(a)為從應力云圖上截取的部分區域，該區域對應的氫濃度分布如圖5(b)所示；在兩張放大圖上設定分析路徑。在邊界應力σ0分別為5,20,50,80,100MPa時，分析路徑上各位置的應力和氫濃度。圖5(c)可見增大邊界應力σ0時，各位置的局部應力σL也隨之線性增大。圖5(d)中分析了距離上邊界分別為3，6，9，14，16，20.6μm等位置(在圖中用Distance 3,Distance 6……表示)的氫濃度，可見各位置的氫濃度隨應力的增大線性增加或減少，其中應力集中系數α>1位置的氫濃度隨應力的增大而線性增加，斜率k為正；而α<1位置的氫濃度隨應力的增大反而線性減少，斜率k為負。圖5(e)對圖5(d)中各直線的斜率k與相應的應力集中系數α用一元二次方程進行擬和，得到經驗式：

(5)

可見，應力驅動對氫擴散的影響可分為3種情況：(1)當α=1.0時，斜率為0，隨外加應力的增大，局部氫濃度不發生改變；(2)當α>1.0時，斜率為正，隨應力的增大，氫濃度隨之增大；(3)當α<1.0，斜率為負，隨應力的增大，氫濃度反而降低。

因此，局部氫濃度的大小由各區域的應力集中系數和應力水平決定。

圖4 彈性剛度梯度(a)和Block尺寸(b)對應力集中系數和氫濃度的影響Fig.4 Effects of elastic stiffness gradient (a) and Block length (b) on the stress concentration and hydrogen concentration

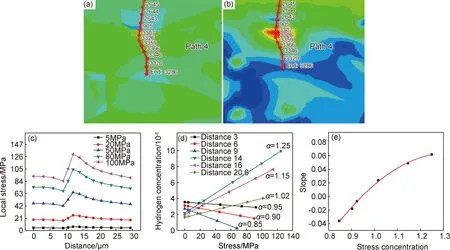
圖5 氫濃度與應力集中系數的關系(a)在應力分布圖上設定分析路徑Path 4；(b)在氫分布圖上設定與應力相同的分析路徑；(c)不同外加應力下的局部應力的變化；(d)局部應力對局部氫濃度的影響；(e)應力集中系數與斜率(氫濃度與應力的線線關系)的擬合關系曲線Fig.5 Relationship between hydrogen concentration and stress concentration(a)Path 4 was set in stress distribution map;(b)Path 4 was set in hydrogen distribution map as same as that in fig.(a);(c) the change curve of local stress under different applied load;(d)the effect of local stress change on local hydrogen concentration;(e) the fitted curve of stress concentration and slope of hydrogen concentration related to stress

3.4 氫脆斷口形貌及解理裂紋的EBSD實驗分析

在快速滲氫溶液和大氣中進行的慢拉伸力學性能實驗結果如表1所示，快速滲氫溶液中的試樣斷后伸長率為0，斷裂強度僅為677MPa，低于大氣中的材料屈服強度850MPa，說明材料尚未發生宏觀塑性變形就已斷裂，斷口微觀形貌如圖6(a)所示，為穿晶準解理的脆性斷裂形態[22]，同一Block板條束內的板條斷裂形態相同，氫脆斷口以Block板條束為結構單元發生穿晶斷裂。大氣環境下的無氫正常拉伸試樣斷口有塑性頸縮，斷后伸長率達到14%，抗拉強度為1034MPa，試樣在屈服極限以上發生塑性斷裂，微觀斷口如圖6(b)所示，為韌窩斷裂形態。對比上述兩種斷口形態可知，是氫引發了滲氫溶液中試樣斷裂的脆性轉變。

遠離斷口的剖面金相上可觀察到3條微裂紋， 裂紋兩側沒有明顯塑性變形，呈現氫脆裂紋的脆性開裂特征。對裂紋附近的組織進行EBSD分析。如圖7(a)所示，可見裂紋主要在彈性剛度差異大的板條處萌生，垂直于裂紋作兩個分析路徑Path 5, Path 6，彈性剛度的變化曲線如圖7(b)所示，裂紋附近的彈性剛度相差較大，在120GPa左右。依據EBSD實驗得到的微區彈性剛度數據對該區域進行微區應力和氫濃度的模擬計算分析，結果如圖7(c),(d)所示，最大應力和最大氫濃度出現的位置與裂紋的產生區域相符，說明裂紋從氫的聚集區萌生，并擴展形成脆性裂紋。

表1 力學性能實驗結果

圖6 慢拉伸斷口分析(a)氫損傷環境下的脆性準解理斷口；(b)大氣下的韌窩斷口Fig.6 Fracture surface analysisof specimen get by slow tensile test (a) the quasi-cleavage fracture morphology under hydrogen damage environment；(b) the dimple fracture morphology under atmosphere

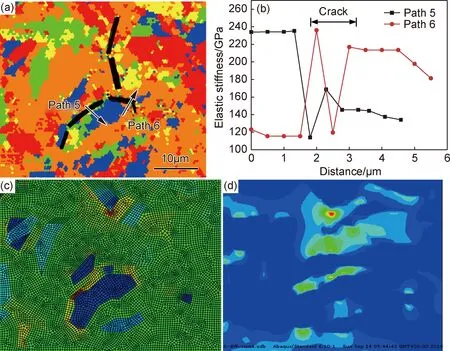
圖7 氫脆裂紋區域的EBSD及數值模擬計算分析(a)氫脆裂紋附近的彈性剛度分布；(b)沿Path 5, 6的彈性剛度變化曲線；(c)施加橫向載荷時的微區應力分布；(d)施加橫向載荷時的氫濃度分布Fig.7 EBSD analysis on crack region and numerical simulation calculation(a)the elastic stiffness distribution for the HB crack region；(b)the change curve of elastic stiffness along Path 5 and Path 6；(c)the stress distribution applied by the load of TD direction；(d)the hydrogen concentration distribution by the load of TD direction

4 討論

4.1 馬氏體組織單元對氫局部富集的影響

板條馬氏體結構鋼依據其尺寸和顯微組織形態，由大到小可劃分[23-25]為原奧氏體晶粒、Packet板條束、Block板條束和Lath板條。同一Block板條束內的各Lath板條由于取向基本一致，其彈性剛度相差較小，不會形成明顯的應力集中和氫的局部富集。相鄰Block板條束的晶體取向不同，板條束間會形成彈性剛度梯度。彈性剛度梯度和組織尺寸越大，Block板條束的應力集中越嚴重，氫的局部富集濃度越高。

由于Block板條束的晶體取向和性能的各向異性，材料在微觀下變形不均勻，微區應力分布主要受Block板條束之間的相互作用的影響，原奧氏體晶界和Packet晶界并不是微區應力集中的特殊位置。氫的擴散由應力主導時，氫會脫離這些晶界氫陷阱，向內部Block板條束應力集中處富集，引發穿晶開裂。這也是許多高溫回火的馬氏體組織結構鋼在進行應力控制下的氫脆實驗時，通常并不是以沿晶方式斷裂，而是以穿晶準解理方式斷裂的原因。但如果氫的擴散不完全由應力控制，或者原奧氏體或Packet晶界的碳化物或雜質偏析較為嚴重，氫在晶界陷阱處的優先富集會最終引發沿晶開裂。

4.2 應力集中系數對氫擴散的影響

上述實驗與模擬計算分析表明，馬氏體微觀組織的彈性剛度呈各向異性，外加應力作用時，應變及氫濃度在不同彈性剛度的組織單元上呈不均勻分布，形成局部應力集中及氫的局部富集。氫的富集程度由應力集中系數和應力大小決定。

彈性剛度梯度大且組織粗大的Block板條束，容易形成較大的應力集中。氫沿應力梯度方向擴散，向應力集中區富集。氫的局部富集程度主要由應力集中系數和應力水平決定：應力集中系數大于1時，氫濃度隨應力的增大而增大；應力集中系數小于1時(即局部應力低于平均應力)，氫濃度隨應力的增大而減少。

應力對氫擴散的驅動現象可用相關文獻在實驗基礎上得到的氫擴散經驗式[26]進行解釋：

(6)

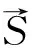
對應力集中系數大于1的區域，dσ/dx為正，氫擴散方向與應力梯度方向相同，外加應力越大，氫溶入的擴散系數也越大，氫濃度隨應力的增大而增大；對應力集中系數小于1的區域，dσ/dx為負，氫擴散方向與應力梯度方向相反，外加應力越大，氫逸出的擴散系數也越大，氫濃度隨應力的增大反而降低。此現象與本研究的數值結果相符。

5 結論

(1)由于板條馬氏體中Block板條束的彈性剛度各向異性，有外力作用時，應力及氫濃度在微觀組織下呈不均勻分布。

(2)可以利用彈性剛度的各向異性計算馬氏體組織的微區應力，Block板條束是表征微區應力的組織單元。

(3)在應力驅動氫擴散的條件下，氫逐漸向高應力處擴散，使高應力區的Block板條束的氫濃度逐漸增加，低應力區的Block板條束的氫濃度逐漸降低。

(4)馬氏體組織的局部氫濃度主要取決于應力集中系數和應力水平，其中應力集中系數決定了氫濃度增大或減少的變化趨勢。

(5)彈性剛度梯度大以及組織粗大的Block板條束組織單元應力集中較為嚴重，聚集較高含量的氫，易萌生氫脆裂紋。

[1] 李永德，徐娜，郭衛民,等. 高壓氣相熱充氫對SUJ2軸承鋼超高周疲勞行為的影響[J]. 材料工程，2014,(2): 87-98.

LI Y D, XU N, GUO W M, et al. The influence of high pressure thermal hydrogen charging on very high cycle fatigue behavior of SUJ2 bearing steel [J]. Journal of Materials Engineering, 2014,(2): 87-98.

[2] AKIHIDE N, SHIGERU K, KOJI I, et al. Visualization of hydrogen transport in high strength steels affected by stress fields and hydrogen trapping[J]. Scripta Materialia, 2001, 45(10): 1227-1232.

[3] 郭昀靜，王春芳，李建錫,等. 利用TDS研究二次硬化鋼中氫的擴散行為[J]. 航空材料學報，2012,32(3)：5-9.

GUO Y J, WANG C F, LI J X, et al. Investigation of hydrogen diffusion in secondary hardening steel by means of thermal desorption spectrometry[J]. Journal of Aeronautical Materials, 2012, 32(3)：5-9.

[4] ZHANG W S, HOU M Q, WANG H Y, et al. Numerical simulation of diffusivity of hydrogen in thin tubular metallic membranes affected by self-stresses[J]. International Journal of Hydrogen Energy, 2004, 29(11): 1165-1172.

[5] KIMURA Y, SAKAI Y, HARA T, et al. Hydrogen induced delayed fracture of ultrafine grained 0.6%O steel with dispersed oxide particles[J]. Scripta Materialia, 2003, 49(11):1111-1116.

[6] HARDIE D, LIU S E.The effect of stress concentration on hydrogen embrittlement of a low alloy steel[J]. Corrosion Science, 1996, 38(5): 721-733.

[7] WANG M Q, AKIYAMA E, TSUZAKI K. Determination of the critical hydrogen concentration for delayed fracture of high strength steel by constant load test and numerical calculation[J]. Corrosion Science, 2006, 48(8): 2189-2202.

[8] BARNOUSH A, VEHOFF H. Recent development in the study of hydrogen embrittlement: hydrogen effect on dislocation nucleation [J].Acta Materialia, 2010, 58(16): 5274-5285.

[9] DOSHIDA T, NAKAMURA M, SAITO H, et al. Hydrogen-enhanced lattice defect formation and hydrogen embrittlement of cyclically prestressed tempered martensitic steel[J]. Acta Materialia,2013, 61(20): 7755-7766.

[10] NEERAJ T, SRINIVASAN R, LI J. Hydrogen embrittlement of ferritic steels: observations on deformation microstructure, nanoscale dimples and failure by nanovoiding[J].Acta Materialia,2012, 60(13): 5160-5171.

[11] ZHAO M J, GUO Z F, CHEN S H, et al. Hydrogen-induced modification in the deformation and fracture of a precipitation-hardened Fe-Ni based austenitic alloy[J]. Journal of Materials Science & Technology, 2014,30(11)：1155-1159.

[12] VENEGAS V,CALEYO F, GONZLEZ J L, et al. EBSD study of hydrogen induced cracking in API-5-5L-X46 pipeline steel [J]. Scripta Materialia, 2005, 52(2):147-152.

[13] LIM H, LEE M G,KIM J H, et al. Simulation of polycrystal deformation with grain and grain boundary effects[J]. International Journal of Plasticity, 2011, 27(27):1328-1354.

[14] TUNG P V, KATJA J, THOMAS B. Simulation of sheet metal forming incorporating EBSD data[J]. Journal of Materials Processing Technology,2012, 212(12): 2659-2668.

[15] NYE J F. Physical Properties of Crystals[M]. London: Oxford University Press, 1985.

[16] THOMAS J H, BRENT L A, DAVID T F, et al. Estimation of the full Nye’s tensor and its gradients by micro-mechanical stereo-inference using EBSD dislocation microscopy[J]. International Journal of Plasticity, 2013, 50: 146-157.

[17] MURA T. Micromechanics of Defects in Solid[M]. Dordrecht, Holland: Matrinus Nijhoff Publishers, 1987.

[18] LUFRANO J, SOFRONIS P. Enhanced hydrogen concentrations ahead of rounded notches and cracks-competition between plastic strain and hydrostatic stress[J]. Acta Materialia, 1998, 46(5): 1519-1526.

[19] ZAKROCZYMSKI T, OWCZAREK E. Electrochemical investigation of hydrogen absorption in a duplex stainless steel[J]. Acta Materialia, 2002, 50 (10): 2701-2713.

[20] 褚武揚. 氫損傷和滯后斷裂[M] . 北京: 冶金工業出版社, 1988.

CHU W Y.Hydrogen Induced Cracking and Delayed Fracture[M].Beijing:Metallurgical Industry Press,1988.

[21] 孫秦，童小燕，楊慶雄. 多晶體材料微結構彈性性質的數值統計分析[J]. 機械強度，1997, 19(1):37-41.

SUN Q, TONG X Y, YANG Q X. Numerical statistical analysis on elastic behaviors of polycrystalline material microstructures [J]. Journal of Mechanical Strength, 1997, 19(1): 37-41.

[22] AKIHIDE N, CYNTHIA D S, MOHSEN D, et al. The role of hydrogen in hydrogen embrittlement fracture of lath martensitic steel[J]. Acta Materialia, 2012, 60(13-14): 5182-5189.

[23] MORITO S,TANAKA H, KONISHI R, et al. The morphology and crystallography of lath martensite in Fe-C alloys[J]. Acta Materialia, 2003, 51(6): 1789-1799.

[24] YOJI M, KOICHI H, HIROKI T, et al. Micro-tension behavior of lath martensite structures of carbon steel[J]. Materials Science and Engineering, 2013, 560(10): 535-544.

[25] KITAHARA H, UEJI R, UEDA M, et al. Crystallographic features of lath martensite in low-carbon steel[J]. Acta Materialia, 2006, 54(5):1279-1288.

[26] 權高峰，宋余九. 應力場中氫擴散的實驗研究[J]. 中國腐蝕與防護學報, 1993, 13(1): 80-85.

QUAN G F, SONG Y J. An experimental study on hydrogen diffusion in stress fields [J]. Journal of Chinese Society for Corrosion and Protection, 1993, 13(1): 80-85.

Microstructure Anisotropy Effect on Stress and Hydrogen Distribution in Micro Area for Martensitic Stainless Steel

ZHONG Zhen-qian1,TIAN Zhi-ling1,YANG Chun1，2

(1 Division of Analysis and Testing,Central Iron and Steel Research Institute,Beijing 100081,China；2 School of Materials and Engineering,Tsinghua University，Beijing 100083,China)

Elastic stiffness distribution of martensite microstructure was analyzed by using Electron Back Scatter Diffraction(EBSD) experiment, based on which the coupled finite element model of stress-hydrogen interaction was established to study the influence of martensitic microstructure anisotropy on the micro local stress and hydrogen distribution. The results show that misorientation between adjacent Block Laths is 60°, and different Block Laths have different elastic stiffness in the same loading direction, which resulted in the heterogeneous distribution of micro stress and hydrogen, and micro stress can be characterized by microstructure element of Block Lath.Elastic stiffness gradient and Block size play a significant role in stress concentration among microstructures, and while stress concentration can affect hydrogen distribution. High elastic stiffness gradient and large size of Block Lath cause high stress concentration, accumulate high concentration of hydrogen, which initiate crack of hydrogen embrittlement in the end. The above results are consistent with micro fracture morphology and EBSD experiment on crack region.

anisotropy;hydrogen diffusion;elastic stiffness;hydrogen embrittlement;FEM;EBSD

10.11868/j.issn.1001-4381.2016.10.012

TG111.5

A

1001-4381(2016)10-0080-08

中國應急分析平臺(2060503)

2014-12-10;

2015-12-28

鐘振前(1979-)，男，博士，高級工徎師，主要從事材料失效分析研究，聯系地址：北京市海淀區高粱橋斜街13號鋼鐵研究總院(100081)，E-mail:13521142587@139.com