第12講“貴了探索型問題”復習精講

韓芬

專題精講

規律探索型問題也是歸納猜想型問題，其特點是：給出一組具有某種特定關系的數、式、圖形，或給出與圖形有關的操作變化過程，或某一具體的問題情境，要求通過觀察分析推理，探究其中蘊涵的規律，進而歸納或猜想出一般性的結論，主要有“數列規律”“計算規律”“圖形規律”與“動態規律”等題型，

規律探索問題的解題方法一般是通過觀察、類比特殊情況（特殊點、特殊數量、特殊線段、特殊位置等）中的數據特點，將數據進行分解重組、猜想、歸納得出規律，并用數學語言來表達這種規律，同時要用結論去檢驗特殊情況，以肯定結論的正確性，

點撥：對于數字規律問題主要是在分析比較的基礎上發現題目中所蘊涵的數量關系，先猜想，然后通過適當的計算回答問題，此題主要考查探尋數字規律問題，注意觀察總結規律，并能正確應用規律，解答此題的關鍵是判斷出：1+3+5+…+（2n-1）=n²，

點撥：對于數式規律問題主要是通過觀察、分析、歸納、驗證，然后得出一般性的結論，以列代數式即函數關系式為主要內容，此題考查數式的規律，通過觀察，分析、歸納并發現其中的規律，并應用發現的規律解決問題，

三.圖形規律型

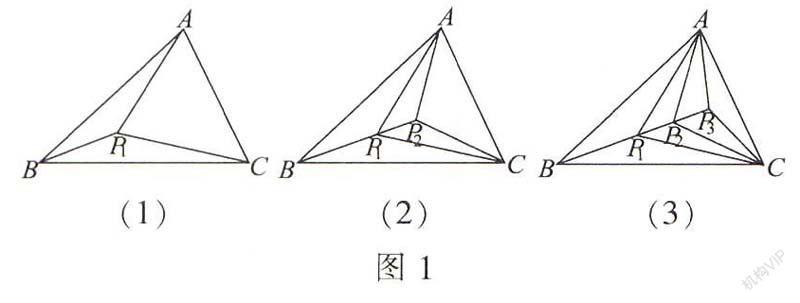
例3（2015·聊城）如圖1（1），△ABC的三個頂點和它內部的點Pl，把△ABC分成3個互不重疊的小三角形；如圖l（2），AABC的三個頂點和它內部的點Pl、P2，把△ABC分成5個互不重疊的小三角形；如圖1（3），△ABC的三個頂點和它內部的點P1、P2、B，把△ABC分成7個互不重疊的小三角形：…△ABC的三個頂點和它內部的點P1、P2、P3、…、Pn，把△ABC分成個互不重疊的小三角形，

點撥：圖形規律問題主要是觀察圖形的組成、分拆等過程中的特點，分析其聯系和區別，用相應的算式描述其中的規律，要注意對應思想和數形結合，本題考查圖形的變化規律類型，對于找規律的題目首先應找出哪些部分發生了變化，是按照什么規律變化的，然后通過分析找到各部分的變化規律，直接利用規律求解，

點撥：對于數形結合猜想型問題首先要觀察圖形，從中發現圖形的變化方式，再將圖形的變化以數或式的形式反映出來，從而得出圖形與數或式的對應關系，數形結合總結出圖形的變化規律，進而解決相關問題，此題主要考查了坐標與圖形變化問題，解答此題的關鍵是判斷出An的橫坐標、縱坐標各是多少，

中考命題預測

1.請觀察下面幾組數：

1，3，5，7，9，11，13，15……2，5，8，1l，14，17，20，23……7，13，19，25，31，37，43，49……

這三組數具有共同的特點，現在有上述特點的一組數，第一個數是3，第三個數是ll，則其第n個數為（

），

A.8n-5

B.n²+2

C.4n-1

D.2n²-4n+5

2.古希臘數學家把數1，3，6，10，15，21，…叫作三角形數，其中l是第一個三角形數，3是第2個三角形數，6是第3個三角形數……依此類推，那么第9個三角形數是____，2 016是第____個三角形數，