實對稱矩陣的合同

程生敏

（鄭州工業應用技術學院基礎教學部 河南鄭州 451100）

實對稱矩陣的合同

程生敏

（鄭州工業應用技術學院基礎教學部 河南鄭州 451100）

關于實對稱矩陣的研究有極其廣泛的內容，本文主要探討了實對稱矩陣的合同標準形、規范標準形和實對稱矩陣的應用等。

實對稱矩陣 合同變換 合同標準形

一、預備知識

定義：在數域P中，n n×矩陣A，B稱為合同的，若有可逆的n n×矩陣C，使'BC AC=。

二、實對稱矩陣的合同標準形、規范標準形等問題

定理1 在數域P上，任意一個實對稱矩陣都合同于一對角矩陣，且任一實對稱矩陣都合同于一個右邊形式的對角矩陣：

其中對角線上1的個數p及-1的個數rp-（r是A的秩）都是唯一確定的，分別稱為A的正、負慣性指數.它們的差2pr-稱為A的符號差。

證明：我們對變量的個數n作歸納法。

分四種情形來討論：

（1） aii（ i=1，2，...，n）中至少有一個不為零，例如a11≠0.取替換

于是A和C1可寫成分塊矩陣，

這里'α為α的轉置，1nE-為1n-級單位矩陣.這樣

這是一個對角矩陣.我們所要的可逆矩陣就是C=C1C2.

（2） a11=0但有一個aii≠0.

這時只要把A的第一行與第i行互換，再把第一列與i列互換，就歸結成上面的情形，根據初等矩陣與初等變換的關系，取

顯然P（1，i）'=P（1，i），矩陣就是把A的第一行與第i行互換，再把第一列與第i列互換的結果，因此，C1'AC左上角第一個元素就是aii，這樣就歸結到第一種情形。

（3） aii=0，i=1，…，n ，但有一a1j≠0，j≠0.

與上一種情形類似，作合同變換P（2，j）'AP（2，j），可以把a1j搬到第一行第二列的位置，這樣就變成了配方法中的第二種情況.與那里的變數替換相對應，取C1=，于是的左上角就是

實數域P上，任意實對稱矩陣都可以變成規范形，且規范形是唯一的［1］

定理2 實對稱陣的特征多項式的根都是實數［1］.

定理3 設A是一個實對稱矩陣，則屬于A的不同特征值的特征向量一定正交［1］.

定理4 設是一個n階實對稱陣，總能找到一個n階正交矩陣P，使P-1AP

為對角陣［1］.

由定理4說明，對任何一個實對稱陣總有正交矩陣存在，使它化為對角陣，具體如何找到這樣的正交矩陣，可按照以下步驟進行：

（2） 對每個λi（i=1，2，…，s）.解特征方程組（λiE-A） X=0，找出它們的一個基礎解系Xi1，Xi2，…，Xiri，這就是矩陣A的屬于特征值λi的線性無關的特征向量；

（3） 用施密特法，將Xi1，Xi2，…，Xiri正交化、單位化，得到一組正交的單位向量組εi1，εi2，…，εiri，它們是A的屬于特征值λi的正交的單位特征向量；

（4） 因為λ1， λ2，…，λs各不相同，ε11，…，ε1r1，ε21，…，ε2r2，…，εs1，…，εsrs它們仍是正交的單位向量組，它們的總數為n個，以這一組向量為列，作一個矩陣P，它就是所要求的正交陣.

三、實對稱矩陣的應用

若pn=，則該矩陣為正定矩陣；若0pn＜＜且0q=，則該矩陣為半正定矩陣；

若0pn＜＜且0qn＜＜，則該矩陣為不定矩陣；若qn=，則該矩陣為負定矩陣；

若0p=且0qn＜＜，則該矩陣為負定矩陣.

合同變換除了保秩性外，還具有保定性，利用后一條性質，可把實對稱矩陣進行合同分類，實n階對稱矩陣按合同分類，可以分為種，這也就解決了怎樣的矩陣是合同的.下面舉例看看實對稱矩陣及其標準型的應用.

例1 設f（ x， y， z）=2y2-8x2-z2-2xy+6xz-2yz，試討論：若（x， y， z）看作k3上的向量，問在k3上f（ x， y， z）是否有非零零點。

解：

由A是實對稱矩陣知A合同于某對角陣，且，

即A為不定陣，由此可得f（ x， y， z）在k3上有非零零點.

例2 設A是n階實對稱矩陣，若有n維向量X1，X2，使則必有實n維向量使

證明 因為A為n階實對稱矩陣，所以有n階可逆矩陣T，使

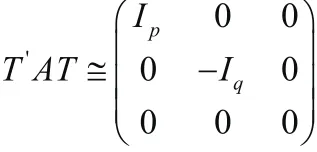
即（TY0）'A（ TY0）=0，令X0=TY0，則

例3 設A是一個n階實對稱矩陣，則A是一個秩為r的半正定矩陣?存在r個線性無關的實n維列向量αi=（a1i，a2i，...，ani）'，i=1，2…，r 使得證明 “?”因A是秩為r的半正定矩陣，所以存在n階實可逆矩陣P，使

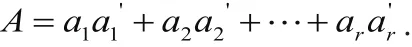
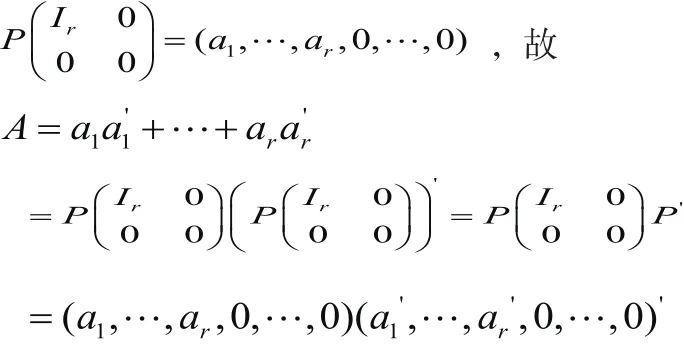
［1］ 王萼芳，石生明.高等代數［M］.第三版.北京：高等教育出版社，2003.

［2］ 陳云龍，鐘立敏.線性代數簡明方程［M］.中國科學技術出版社，1989.

［3］ 陳維新.線性代數［M］.北京：北京科學出版社，2000.

［4］ 孫蘭芳，陳一巾.線性代數［M］.浙江：浙江大學出版社，1994.

［5］ 同濟大學應用數學系.高等數學（第五版）［M］.北京：高等教育出版社，2001.