不等式恒成立解題策略
福建省沙縣一中 黃仍洪
不等式恒成立解題策略
福建省沙縣一中 黃仍洪
不等式 函數 高考
不等式恒成立是一類常見且重要的問題,這類問題因為既含參數又含變量,具有形式靈活、思維性強、不同知識交匯等特點,在解題時對問題要有充分的認識理解,否則若理解偏差,或對問題的認識有誤,都會導致解題錯誤,造成不必要的失分,本文結合教學實踐就不等式恒成立的幾類問題進行舉例剖析,重點是分析它們的解題策略和注意事項與大家分享.
問題一注意所研究不等式恒成立的類型
例1(1)已知關于x的不等式x2+ax+1〉0恒成立,求參數a的取值范圍.
(2)已知關于x的不等式ax2+ax+1〉0恒成立,求參數a的取值范圍.
分析:本例中的兩個小題都是一個關于x的不等式恒成立的問題,稍不注意都易把它們當成是關于x的一元二次不等式恒成立的問題,實際上問題(1)確實是一個關于x的一元二次不等式恒成立的問題,所以結合二次函數 f(x)=x2+ax+1的圖像,必須整個函數的圖像都在x軸的上方,從而只要Δ=a2-4〈0得到-2〈a〈2;
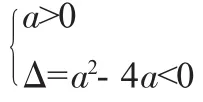
本例特別注意點是問題(2)的易忽略a=0.
問題二注意不等式恒成立轉化中符號的影響
例2(1)已知不等式x2+ax+1〉0對一切x∈(0,+∞)恒成立,求參數a的取值范圍.
(2)已知不等式x2+ax+1〉0對一切x∈(-2,2)恒成立,求參數a的取值范圍.
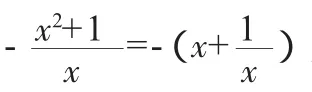
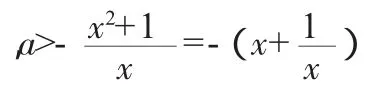
本例應注意點是(2)在分離過程中自變量的取值對不等號方向的影響,也就是分離參數不等式轉化過程中注意不等號的方向是否改變問題,若涉及符號變化,則應進行分類討論處理.
問題三注意問題轉化過程的含義和要求
例3(1)已知函數y=lg(2x2+mx+1)的定義域為R,求實數m的取值范圍.
(2)已知函數y=lg(2x2+mx+1)的值域為R,求實數m的取值范圍.
分析:本例中兩小題從題目表面來看區別不大,但實際上在轉化為恒等式的過程中還是存在很大的區別的.
問題(1)是函數的定義域為R,也就是不論x為何值,函數y=lg(2x2+mx+1)均有意義,所以不等式2x2+mx+1〉0恒成立,應滿足Δ=m2-8〈0,得;而問題(2)是值域為R,根據對數函數性質,這時必須保證2x2+mx+1能得到所有的正數,所以結合二次函數的圖像知,滿足的關系是2x2+mx+1的最小值不大于0,于是有Δ=m2-8≥0得到或
問題四注意全稱命題和特稱命題成立的區別
例4(1)命題“?x∈[-2,3],m<x2+2x+2”是真命題,求出m的取值范圍;
(2) 命題“?x∈[-2,3],m<x2+2x+2”是真命題,求出m的取值范圍;
分析:命題“?x∈[-2,3],m<x2+2x+2”是真命題即對一切[-2,3]上的實數x,不等式恒成立;形如“a≥f(x)”或“a≤f(x)”是不等式恒成立問題中最基本的類型,其實質是不等式恒成立中最常見的問題“a≥f(x)在x∈D上恒成立,則a≥f(x)max(x∈D),a≤f(x)x∈D上恒成立,則a≤f(x)min(x∈D)”;因為f(x)=x2+2x+2在[-2,3]的最小值為1,所以命題“?x∈[-2,3],m<x2+2x+2”是真命題,則m的取值范圍是m〈1.
命題“?x∈[-2,3],m<x2+2x+2”是真命題即在[-2,3]上存在實數x,使不等式成立;這是不等式成立中的另一類常見問題,存在x∈D,a≥f(x)成立,則 a≥f(x)min(x∈D);存在x∈D,a≤f(x)成立,則a≤f(x)max(x∈D);f(x)=x2+2x+2在[-2,3]的最大值為17,所以命題“?x∈[-2,3],m<x2+2x+2”是真命題,m的取值范圍是m<17即可.
問題五 注意f(x)〉g(x)恒成立與f(x1)〉g(x2)恒成立的區別
分析:f(x)≤g(x)恒成立問題轉化為[f(x)-g(x)]max≤0恒成立;而f(x1)〈g(x2)恒成立問題轉化為f(x)max〈g(x)min恒成立.
問題(1)解法:f(x)≤g(x)在x∈[0,1]恒成立在x∈[0,1]恒成立在x∈[0,1]上的最大值小于或等于零.
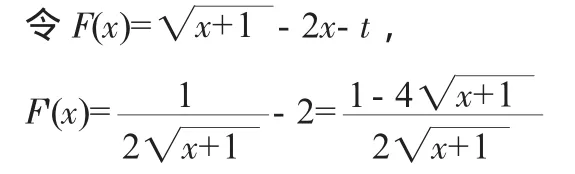
∵x∈[0,1], ∴F'(x)〈0即F(x)在[0,1]上單調遞減,
∴f(x)≤F(0)=1-t≤0,即t≥1.
問題(2)解法:對任意x1,x2∈[-2,2],都有f(x1)〈g(x2)成立,等價于x∈[-2,2],
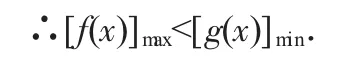
∵f'(x)=x2-2x-3,令f'(x)〉0得x〉3或x〈-1;得f'(x)〈0.
∴f(x)在[-2,-1]為增函數,在[-1,2]為減函數.
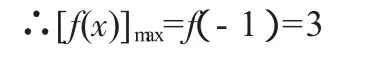

問題六注意正確選用和理解問題中的參數
例6對于滿足0≤p≤4的一切實數,不等式x2+px〉4x+p-3恒成立,試求 x的取值范圍.
分析:在解決不等式恒成立問題時,一種最重要的思想方法就是構造適當的函數,然后利用相關函數的圖像和性質解決問題,但若是一個含多個變量的數學問題時,需要確定合適的變量和參數,從而揭示函數關系,才會使問題更加清晰明了;人們都習慣把x當作自變量,即這時的函數為y=x2+(p-4)x+3-p,于是問題轉化為:當p∈[0,4]時,y〉0恒成立,求x的取值范圍.解決這個問題需要用到二次函數以及二次方程的區間根原理,是相當復雜的.這時如果能適時地把主元變量和參數變量進行“換位”,往往會使問題降次、簡化.一般來說,已知存在范圍的量視為變量,而待求范圍的量視為參數.
解:設函數f(p)=(x-1)p+(x2-4x+3),顯然x≠1,則f(p)是p的一次函數,要使f(p)〉0恒成立,當且僅當f(0)〉0且f(4)〉0時,解得x的取值范圍是(-∞,-1)∪(3,+∞).
本例注意點是很容易把問題簡單地等價轉化為一個二次不等式問題,解題的關鍵是正確選用和理解問題中的參數.

