確定性信號分解與平穩隨機信號分解的統一研究

王宏禹，邱天爽

（大連理工大學電子信息與電氣工程學部，遼寧 大連 116024）

確定性信號分解與平穩隨機信號分解的統一研究

王宏禹，邱天爽

（大連理工大學電子信息與電氣工程學部，遼寧 大連 116024）

對確定性信號分解與平穩隨機信號分解進行了深入統一的研究。首先根據線性系統穩定性理論，分別給出正則穩定情況下與邊界穩定情況下2種信號分解的統一研究結果。然后根據線性空間投影理論，分別給出正交投影情況下與自投影情況下2種信號分解的統一研究結果。前一種研究明確具體且物理意義清晰，后一種研究數學意義與幾何意義清晰，將兩者合在一起研究，相得益彰。

信號分解；線性系統；正則穩定；邊界穩定；線性空間；正交投影；自投影

1 引言

確定性信號與平穩隨機信號的分解或展開已有許多研究[1～5]，已為眾所熟知。這2種信號（包括連續的與離散的、有限的與無限的）有許多共性，可對它們進行統一研究。不過，據文獻調研，目前尚未見到這種研究。為此，本文對這2種信號分解進行了統一研究。由于確定性離散信號與平穩隨機離散信號（以下均略去“離散”）可分別由{δ(n)}與白噪聲序列{w( n)}激勵一線性時不變離散系統（以下均簡稱為線性系統）所產生，所以這2種信號可由線性系統理論統一起來研究。線性系統穩定性分為正則穩定的與邊界穩定的，前者為人們熟悉，后者卻不熟悉。本文對這2種信號于線性系統正則穩定與邊界穩定情況下的信號分解，給出了統一研究結果。對這2種信號的共性，可由數學泛函分析的線性空間理論統一研究。線性空間投影分為正交投影與自投影，前者為人們熟悉，后者卻不熟悉，本文對這2種信號于線性空間正交投影與自投影情況下的信號分解，給出了統一研究結果。

2 線性時不變離散系統及其穩定性

設因果線性時不變離散系統（以下為了簡便起見，再次將其簡稱為線性系統）的傳遞函數H( z)為有限階m和n的有理函數[5]

式(1)可表示為如下的零、極點模型，有

在式(2)中，分子項與分母項為1時分別對應于全極點模型與全零點模型。

H( z)為全極點模型時，將其展開為部分分式，當它所有極點不同時，有

與H( z)對應的格林函數g( k)或脈沖響應h( k)為

由此可見，當k→∞時，使g( k)=h( k)→0的唯一條件是λi＜1，i=1,2,…,n 。如果λi＞1，則當k→∞時，g(k)將無限增長。因此，對線性系統，若H( z)所有極點均位于單位圓內時，系統是穩定的，而H( z)只要有極點在單位圓外時，系統是不穩定的。由于極點全部位于單位圓內，有限階全極點模型可以化為無限階全零點模型，所以，若線性系統是穩定的，則必定是因果的最小相位或最小時延系統。

若H( z)的極點位于z平面的單位圓上，線性系統處于穩定與不穩定的邊界，其穩定性要視極點在單位圓上的位置與H( z)是否有相同的極點而定。當H( z)在單位圓上有l個相同極點時，則其格林函數gl( k)或脈沖響應hl( k)為

1) 極點位于單位圓實軸上，即λi=1,i=1,2,…,l。對l=1，為1階極點情況，g1( k)=h1( k)=C（C為常數）。對l=2，為2階極點情況，g2(k)=h2( k)=C1+C2k （C1、C2為常數），它為k的線性增長函數，對l一般情況，有

它為k的l?1階多項式增長函數。

2) 在z平面單位圓上有一個一階共軛極點時，即λ1,2=e±jω，由式(5)有

即g( k)=h( k)為穩定的等幅正弦與余弦振蕩函數。式(7)中常數a=C1+C2，常數b=j(C1?C2)。

若g( k)=h( k)在z平面單位圓上共有n個不同的一階共軛極點時，則

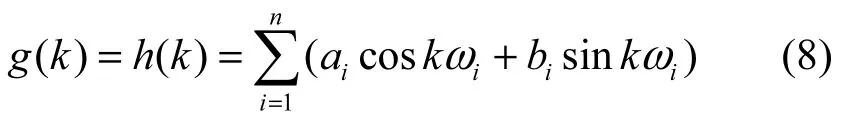
為n個不同頻率的穩定等幅正弦與余弦振蕩函數。

若g( k)=h( k)在z平面單位圓上有l（1＜l≤n）個相同共軛極點時，則

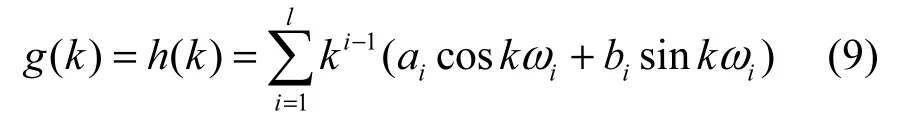
為l(1＜l≤n)個不同頻率且幅度增長的正弦與余弦振蕩函數。

由此可見，當g( k)=h( k)為常數與單個或多個等幅正弦與余弦振蕩函數時，線性系統是邊界穩定的；當g( k)=h( k)為一線性增長、多項式曲線增長與單個或多個不同頻率增長的正弦與余弦振蕩函數時，線性系統是邊界不穩定的。

由以上研究，線性系統的穩定性分為穩定的與邊界穩定的，本文為了使兩者區分更加清楚，對穩定的情況，改稱為正則穩定的情況，因線性系統這種穩定情況是眾所熟知的。

3 基于線性系統穩定性理論的信號分解

由于確定性（離散）信號與平穩隨機（離散）信號分別由{δ(n)}與白噪聲序列{w( n)}激勵一線性系統所產生，故這2種信號分解可由線性系統理論統一研究。因線性系統穩定性有正則的與邊界穩定的2種情況，需要對它們分別進行研究。

3.1 線性系統正則穩定情況下的信號分解

正則穩定的線性系統有3種描述方式：z域傳遞函數或時域格林函數、零極點模型、線性差分方程，這3種描述方式可以互相轉換，可以從任何一種得到另外一種。欲利用正則穩定的線性系統對確定性信號與平穩隨機信號的信號分解進行統一研究，以采用格林函數描述方式為最佳，其理由如下。

1) 數學物理意義清楚，并為人們熟悉。這易由圖1中線性系統的輸入輸出關系而得到。

圖1線性系統輸入與輸出關系

圖1中確定性信號x( n)為

平穩隨機信號x( n)為

2) 便于與后面研究的線性空間投影理論相聯系，得到幾何意義解釋。

對應于線性空間理論研究，{δ(i)}可以視為標準正交基組同樣，白噪聲w( n)是正交的，若其方差σ2=E[ w2( n)]=1，也可視為標準正交基組。這樣，確定性信號x( n)與平穩隨機信號x( n)均可視為線性空間中的一個矢量，信號分解就是將x( n)矢量分解（或投影）到標準正交基上，g( i)是x( n)在相應基上的坐標，如圖2所示。圖2中，ei?δ(i) 時，為確定性信號x( n)在線性空間中的分解情況，而ei?w( i)時，為平穩隨機信號x( n)在線性空間中的分解情況。

圖2信號x( n)的矢量分解

3) 可推廣研究非平穩確定性信號與非平穩隨機信號的分解，詳見文獻[5]。

對正則穩定的線性系統，要求其n階全極點模型的極點λi不同，并且λi＜1,i=1,2,…,n 。現對確定性信號與平穩隨機信號的統一研究，使用的是線性系統的格林函數g( k)，對它所要求的條件也應研究清楚。先考慮一階極點模型，它可化為一無窮階全零點模型如下

對式(12)最后表示式進行因式分解，當λ＜1時，顯見其所有零點必須在單位圓內，此種情況，稱為最小時延系統或最小相位系統。與式(12)H( z)對應的格林函數g( k)或脈沖響應h( k)為

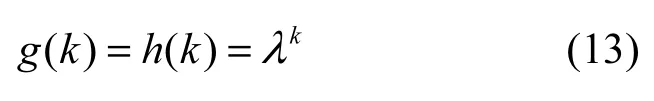
當k=0,1,2,…時，得序列{g( k)}={h( k)}={1,λ,λ2,…}，若λ＜1，則{g( k)={h( k)}是因果最小時延序列或因果最小相位序列。此種一階極點模型研究結果，可以推廣到λi＜1(i=1,2,…,n )且各λi不同的n階全極點模型情況，它就是λi＜1(i=1,2,…,n )時的式(3)與式(4)。

綜上研究，正則穩定的線性系統必定是因果的最小時延系統或最小相位系統，而此種線性系統用格林函數描述時，格林函數序列{g( k)}應該是因果的最小時延或最小相位序列。

3.2 線性系統邊界穩定情況下的信號分解

1) 邊界穩定線性系統的格林函數與差分方程

邊界穩定線性系統的格林函數g( k)=h( k)為常數與單個或多個不同等幅與頻率的正弦與余弦函數組成，現研究與其對應的線性差分方程。先考慮如下單個等幅正弦函數情況

其中，b為正弦函數的幅度，?為相位。由三角恒等式

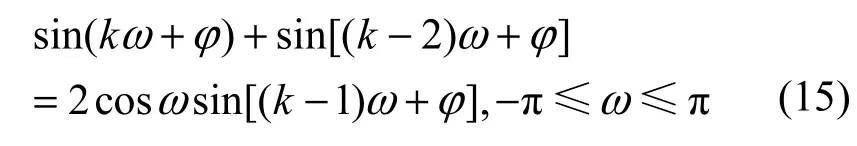
結合式(14)和式(15)有

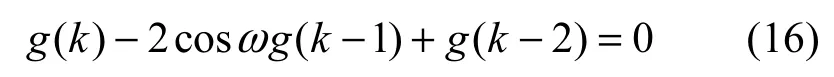
將式(16)表示成一般線性差分方程形式，有

式(17)中，a1=2cosω，a2=?1。式(17)為一零輸入二階線性時不變差分方程。若線性系統由n個不同等幅與頻率及相位的正弦函數組成時，即

則可得零輸入2n階線性時不變差分方程，為

式(19)是1個零輸入2n階線性時不變差分方程。對此種零輸入差分方程，由于g( k)可由g( k)的過去值g( k?i)（i=1,2,…,2n ）線性組合精確確定或精確預測，因此，對凡是零輸入差分方程，其所描述的信號x( k)是可精確確定或可精確預測的。

對正則穩定的線性系統，其格林函數g( k)定義為δ(n)輸入時線性系統的輸出。現對邊界穩定線性系統，無需δ(n)輸入。系統會自激而產生正弦與余弦振蕩。因此，前者定義的格林函數g( k)對后者并不適用。為此，對邊界穩定的線性系統，應尋求格林函數以外比較合適的定義方式。本文將系統自激所產生正弦與余弦振蕩函數的線性組合定義為奇異的格林函數，表示為g(s)(k)。這樣，由式(18)可得g(s)(k)的一般表示式為

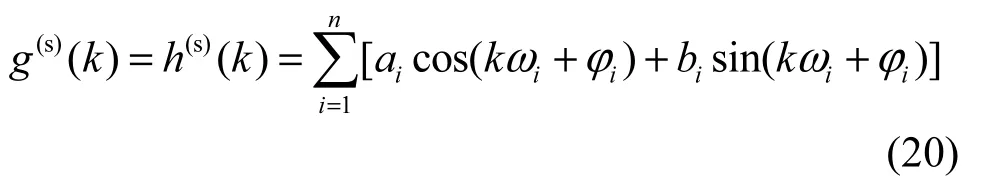
g( k)與g(s)(k)對比關系如表1所示。

表1g(k)與g(s)(k)的對比關系

2) 線性系統邊界穩定情況下的平穩隨機信號

線性系統邊界穩定情況下的正弦與余弦函數經平穩隨機變量調制，可以得到平穩隨機信號[6,7]，常見的有如下情況。

① 調相平穩隨機信號

設單個信號時

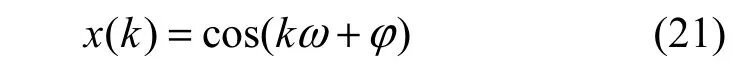
式(21)中ω為常數，?為在[?π,π]均勻分布的隨機變量，其概率密度在。因x( k)的自相關函數r( l)為

上式后一項消失，故

由此可見，r( l)與時間k無關，故x( k)是平穩隨機的。若

式(22)中Ai與ωi為常數，?i為[?π,π]均勻分布的隨機變量，其概率密度在?π≤?≤π為1，2π i=1,2,…,n 。x( k)的自相關函數r( l)為

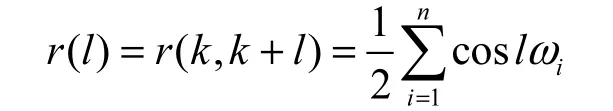
可得到式(22)的x( k)是平穩隨機的。

② 調幅平穩隨機信號

復正弦調幅信號x( k)為

式(23)中ωi是常數，ai是互不相關的隨機變量，其均值為零，方差σi2=E[ ai2],i=1,2,…,n 。x( k)的自相關函數為

實正弦與實余弦調幅信號x( k)為

在式(25)中，ai與bi是互不相關的實隨機變量，均值為零，且的自相關函數為

由于式(24)與式(25)、式(23)與式(25)的調幅復正弦與實正弦與實余弦信號都是平穩隨機的，并且不難得出調幅與調相平穩隨機信號的一般表示式為

其中，ωi為常數，ai、bi與?i為隨機變量，且ai與bi互不相關，為概率密度的均勻分布，i=1,2,…,n 。

對上述3種平穩隨機信號，與調幅及調幅調相平穩隨機信號對應的線性差分方程是線性隨機變量系數的隨機差分方程，現尚未見到文獻介紹，只有調相平穩隨機信號對應的線性差分方程是線性常系數隨機差分方程，可以對其進行研究。將式(22)改寫為

它是一個零輸入的隨機差分方程。

平穩隨機序列{x( n)}，其現在值x( n)是不能由其過去值x( n?i)( i=1,2,…)精確確定或精確預測的，但有的文獻將預測誤差ε(n)的σ2=E[ε2(n) ]為零時，定義為在均方意義下可精確確定或可精確預測的，即

式(30)可進一步表示為

上式即式(29)。這樣，可知式(29)所示的零輸入隨機差分方程是均方意義下可精確確定或可精確預測的。

3) 線性系統邊界穩定情況下信號分解的統一研究

由式(19)線性系統邊界穩定情況下的奇異格林函數g(s)(k)，也就是此種情況下確定性信號x( k)的分解表示式，即

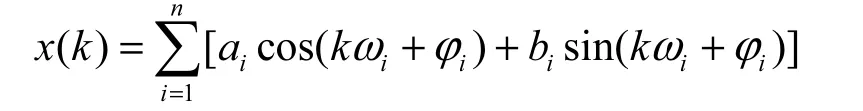
它與平穩隨機信號x( k)分解表示式(27)相同，因此，可在數學上將兩者統一起來。但應明確，對確定性信號x( k)，ai、bi、ωi和?i均為常數，而對于平穩隨機信號x( k)，ωi為常數，ai與bi是不相關的且有相同方差的隨機變量，?i是在[?π,π]均勻分布的隨機變量。

綜上所述，線性系統在邊界穩定情況下，系統可以自激而產生正弦與余弦振蕩，將它們線性組合起來，而產生所需要的信號。對此，在信號分析與處理中，稱其為調和過程，以區別他激線性系統產生信號的一般線性過程。

4 基于線性空間投影理論的信號分解

利用線性空間投影理論來研究確定性與平穩隨機信號的分解[8～12]，不僅可使這2種信號分解在泛函數學框架下統一起來，并可從空間幾何意義上對它們了解得更加清楚。

1) 幾種線性空間的意義與關系

由信號序列或數據序列X={x1, x2,…}組成的線性空間，若信號x是穩定的，其能量需是有限的，即。此種線性空間稱為l2空間。可表示成內積與P=2的范數（P范數定義為，即

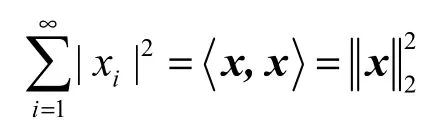
從而有內積線性空間與賦范線性空間。由于范數有不同定義方式，它可不等于內積，對內積等于范數的線性空間，稱為希爾伯特空間，表示為H( X)。由此可見，這4種線性空間意義是相同的。線性空間引入內積后，就可以把許多平面幾何性質推廣到n維或無窮維抽象空間。線性空間引入范數，就可以進行極限運算，以表明信號分解是收斂的，即xk的極限為x，是指，稱xk均方收斂于x，并表示為

對平穩隨機信號的研究，若ξ與η是隨機變量，有：①內積是指；②范數是指；③ξ與η正交是指E[ξη]=0；④ξn收斂于ξ是指。這樣，對確定性信號與平穩隨機信號在數學表示上可進行統一研究。

2) 希爾伯特子空間投影

在希爾伯特子空間中，由非正交不相關的信號序列X={x1, x2,…,xn}所張成的子空間，將其表示為Hn(X)=span{x1, x2,…,xn},xn在子空間Hn?1(X)=span{x1, x2,…,xn?1}的投影表示為x?n，投影誤差為εn，則有

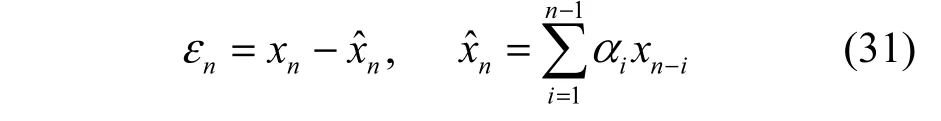
式(31)中αi為待定的線性組合系數。式(31)的關系如圖3所示，εn⊥Hn?1(X )，εn與Hn?1(X )中各元素x1, x2,…,xn?1都正交。

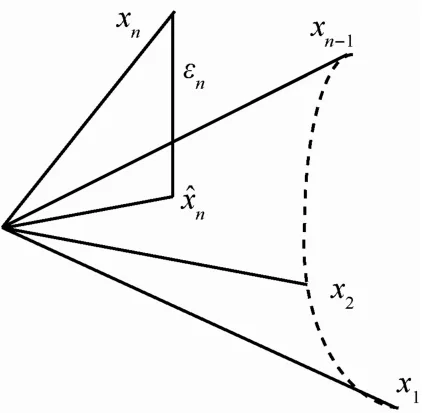
圖3εn在Hn?1(X)投影

nn穩隨機信號的研究中，x?n為均方誤差E[( xn?)2]=E[]最小對x的線性最優估計或最優一步預測，n在最優一步預測中，εn是不線性依賴于xn過去值而出現的新息。通常在希爾伯特子空間中研究的都是這種情況的投影，將其稱為正則投影。

在對確定性信號研究中，若εn=0，則，即xn在子空間Hn?1(X )的投影是其自己，現將這種投影稱為自投影或奇異投影。這種情況的投影，Hn(X)≡Hn?1(X )，對所有n均成立，即所有子空間Hi( X),i=n, n?1,…是相同的。另外，xn可由其過去值xn?1,xn?2,…精確確定。在對平穩隨機信號研究中，應明確的是為均方意義下的自投影或奇異投影，而xn可由其過去值xn?1,xn?2,…在均方意義下精確確定或精確預測。

根據上述，信號x在希爾伯特子空間上的投影分為2種，一種是正則投影，用xu表示，另一種是自投影，用xv表示。若xu與xv是不相關的，且是同時存在的，則有

現在需要研究的是信號分解的問題。首先要解決如何將x分成為xu與xv，這涉及使用格萊姆—施密特（Gram-Schmidt）正交化方法，應對其做必要的介紹與研究。

3) 格萊姆—施密特正交化方法

格萊姆—施密特正交化方法是將非正交的線性不相關序列X={x1, x2,…,xn}化成為正交的線性不相關序列{ε1,ε2,…,εn}，n可以是有限的，也可以是無限的。該方法的基本思路是選擇x1作為ε1；其次，將x2關于x1進行正交分解并選擇與ε1正交的分量作為ε2，于是有；再次，將x3關于空間{ε1,ε2}進行正交分解，并選擇正交于{ε1,ε2}的分量作為ε3。類此不斷繼續下去，直至完成處理過程。這種方法的表示式為

若{ε1,ε2,…,εn}欲成為X的標準正交基，需要對式(33)進行歸一化處理，得

格萊姆—施密特正交化過程可理解為前一希爾伯特子空間Hi?1(X )增加一個正交基εi以得到后一子空間Hi( X),i=2,3,…,n ，從而成為不斷擴大其子空間的過程，如表2所示。

表2格萊姆—施密特正交化過程與H(X)子空間擴大過程關系

表2中，⊕表示“直和”或“正交和”。由表2可得Hn(X)由其子空間Hi( X),i=1,2,…,n ?1擴大過程的表示式，為

4) 希爾伯特子空間的正交投影

線性不相關的非正交信號序列X={x1, x2,…,xn}經格萊姆—施密特正交化方法可化為線性不相關的歸一化正交信號序列E={e1, e2,…,en}，這樣，利用x∈Hn(X )的線性子空間投影可將其轉化為在Hn(E)的線性子空間投影。當k＜n時，x在Hn(E)=span{e1, e2,…,ek}子空間的投影為

當k=n時，由于x在Hn(E)中的投影mn就是它自己，即mn=x，因此，得

式(37)被稱為x在希爾伯特子空間Hn(E)的正交投影。

5) 線性空間正則投影信號xu與自投影信號xv

xu的希爾伯特空間為H( X)=span{,,…}。xv的希爾伯特空間為H( X)=span{,,…}。若xu與xv不相關，x=xu+xv，則H(x)=H(xu)+H( xv)。H( xu)與H( xv)∈H( x)，且處在2個不相交相鄰的H( x)子空間上。為此，可令H( Xu)∈H∞(X )，H( Xv)∈H?∞(X )，這是非常合理的。

對xu采用希爾伯特子空間正交投影法，當n=∞時，由式(37)得信號分解式

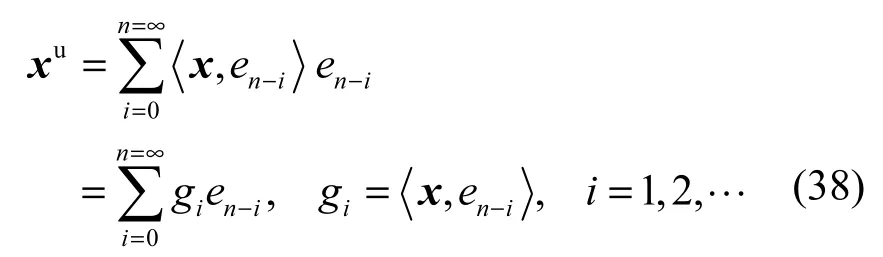
這種情況與線性系統正則穩定情況下的信號分解式(10)相對應，因此，式(38)中標準正交基上的坐標gi對應于式(10)的最小延時或最小相位的格林函數g( i)。

由表2可知，格萊姆—施密特的正交化過程是{ε1}→{ε1, ε2}→{ε1, ε2,ε3}→…→{ε1, ε2,…,εn}，H( X)子空間擴大化過程是H1(X)→H2(X)→H3(X)→…→Hn(X )，則它們的逆過程應分別為去正交過程{ε1, ε2,…,εn}→{ε1, ε2,…,εn?1}→…→{ε1}與H( X)子空間減少過程Hn(X)→Hn?1(X )→…→H1(X)。現采取H( X)子空間減少過程，將xu∈H∞(X)從H( X)=H∞(X)+H (?∞)中分出，得到xv∈H?∞(X)，表示為

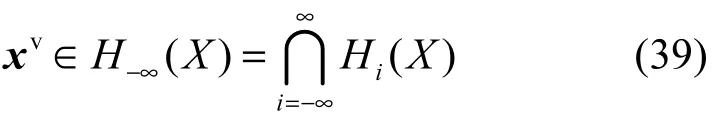
式(39)是與式(35)相對應的逆過程表示式。xv是自投影的，H(Xv)=H(Xv)，對所有n均成立。n n?1這樣，可由其過去值,,…精確確定。

5 與信號沃爾德（Wold）分解關系

信號沃爾德分解任意平穩隨機信號x可以分解為xu和xv2個平穩隨機信號之和，x=xu+xv，其中，xu是平穩隨機MA(∞)信號，即

式(40)中，wn是白噪聲序列。xu是不可精確預測的隨機信號，也稱為正則的隨機信號。xv與xu不相關，它是均方意義可精確預測的隨機信號，也稱為奇異的隨機信號。

對上述信號沃爾德分解，已有一些文獻研究[13～15]，并給出了嚴格數學證明，但均繁難，不易理解。本文研究與其研究有相似之處，但存在完全不同之處，有自己的許多新發展。

本文研究與信號沃爾德分解研究相似之處是均應用了泛函線性空間理論，一個是從線性空間投影理論研究，另一個是從線性空間預測理論研究。

本文研究與信號沃爾德分解研究完全不同之處主要有2個方面。1) 本文是對確定性信號分解與平穩隨機信號分解進行了統一理論研究，而信號沃爾德分解是僅對平穩隨機信號的理論研究。2) 本文提出了新的基于線性系統穩定性的信號分解統一理論，它分為z域單位圓內正則穩定的正則信號分解及z域單位圓上邊界穩定的奇異信號分解，而奇異信號分解是正弦與余弦函數的線性組合。因此，它非常具體明晰，可從物理意義上了解清楚，這非常有助于解決依據線性空間理論信號分解的統一研究中在這方面的不足之處。

6 結束語

本文依據線性系統穩定性理論與線性空間投影理論，給出了確定性信號與平穩隨機信號的信號分解統一研究結果。前者的研究具體明確且物理意義清晰，后者的研究數學與幾何意義清晰，對兩者合在一起研究，可相得益彰，有助于對信號沃爾德分解的研究。本文具有研究新發展前景，主要表現在2個方面。1) 確定性信號與平穩隨機信號的信號分解，各自均可分成為正則信號分解與奇異信號分解，它們可有不同的線性組合方式，例如平穩隨機信號的正則信號與確定性信號的奇異信號，它們的線性組合是方差平穩隨機信號或均值具有趨向性的非平穩隨機信號。因此，對它們的一些線性組合方式進行研究，是有創新發展前景的。2) 本文依據線性系統穩定性理論對信號分解的統一研究，可推廣研究非平穩確定性信號與非平穩隨機信號的統一研究，作者已對此做了研究，參見文獻[5]。

[1]王宏禹. 信號處理相關理論綜合與統一法[M]. 北京: 國防工業出版社, 2005.WANG H Y. Synthesis and unification method in correlation theory of signal processing [M]. Beijing: National Defense Industry Press, 2005.

[2]王宏禹. 信號處理方法與應用[M]. 北京: 機械工業出版社, 2008.WANG H Y. The methods and applications of signal processing[M].Beijing: China Machine Press, 2008.

[3]王宏禹, 邱天爽, 陳喆. 非平穩隨機信號分析與處理（第二版）[M].北京: 國防工業出版社, 2008.WANG H Y, QIU T S, CHEN Z. Non-stationary random signal analysis and processing (second edition)[M]. Beijing: National Defense Industry Press, 2008.

[4]王宏禹, 邱天爽. 微分方程格林函數法的研究[J]. 信號處理, 2015,31(4): 379-385.WANG H Y, QIU T S. Study on the differential equation using the Green’s function[J]. Signal Processing, 2015, 31(4): 379-385.

[5]王宏禹, 邱天爽. 非平穩確定性信號與非平穩隨機信號統一分類法的探討[J]. 通信學報, 2015, 36(2): 2015028.WANG H Y, QIU T S. Unified classification methods for determinate nonstationary signals and random nonstationary signals[J]. Journal on Communications, 2015, 36(2): 2015028.

[6]PRIESTLEY M B. Spectral analysis and time series[M]. London:Academic Press Inc, 1981.

[7]PAPOULIS A. Probability, random variables and stochastic processes[M]. New York: McGraw-Hill, 1984.

[8]KAY S M, MARPLE S L. Spectrum analysis: a modern perspective[J].Proc IEEE, 1981, 69(11):1380-1419.

[9]ROBINSON E A. A historical perspective of spectrum estimation[J].Proc IEEE, 1982, 70(9):885-907.

[10]李冬海. 頻譜估計理論與應用[M]. 西安: 西安電子科技大學出版社, 2014.LI D H. Spectrum estimation theory and application[M]. Xi’an: Xidian University Press, 2014.

[11]BREZINSKI C. Projection methods for liner systems[J]. Journal of Computational and Applied Mathematics, 1997, 77(1): 35-51.

[12]GALANTAI A. Projectors and projection methods[M]. Springer Science amp; Business Media, 2013.

[13]ANDERSON T W. The statistical analysis of time series[M]. John Wiley amp; Sons, 2011.

[14]LINDQUIST A, PICCI G. Linear stochastic systems: a geometric approach to modeling, estimation and identification[M]. Springer, 2015.

[15]FRAZHO A E. Complements to models for noncommuting operators[J]. Journal of Functional Analysis, 1984, 59(3): 445-461.

Unified study on the decomposition for deterministic signals and stationary random signals

WANG Hong-yu, QIU Tian-shuang
(Faculty of Electronic Information and Electrical Engineering, Dalian University of Technology, Dalian 116024, China)

The unified decomposition theories and methods for deterministic signals and stationary random signals were deeply studied. According to the stability theory of linear systems, the unified results of signal decomposition under both regular stable and boundary stable conditions were given respectively. The unified results of signal decomposition under both orthogonal projection and self projection conditions were also provided based on the linear space projection theory.The former is clear and definite in its physical meaning, and the latter is clear in its mathematical and geometrical meanings. They are both complement with each other.

signal decomposition, linear system, regular stability, boundary stability, linear space, orthogonal projection,self projection

The National Natural Science Foundation of China (No.61172108, No.61139001, No.81241059, No. 61671105)

TN911.7

A

10.11959/j.issn.1000-436x.2016189

2015-10-14；

2016-08-25

邱天爽，qiutsh@dlut.edu.cn

國家自然科學基金資助項目（No.61172108, No.61139001, No.81241059, No.61671105）

王宏禹（1929-），男，北京人，大連理工大學教授、博士生導師，主要研究方向為信號信息處理。

邱天爽（1954-），男，江蘇海門人，博士，大連理工大學教授、博士生導師，主要研究方向為信號信息處理。