基于?1稀疏正則化的信源個數(shù)估計(jì)新算法

金芳曉，邱天爽，王鵬，夏楠，李景春

（1. 大連理工大學(xué)電子信息與電氣工程學(xué)部，遼寧 大連 116024；2. 國家無線電監(jiān)測中心，北京 100037）

基于?1稀疏正則化的信源個數(shù)估計(jì)新算法

金芳曉1，邱天爽1，王鵬1，夏楠2，李景春2

（1. 大連理工大學(xué)電子信息與電氣工程學(xué)部，遼寧 大連 116024；2. 國家無線電監(jiān)測中心，北京 100037）

針對現(xiàn)有信號源個數(shù)估計(jì)相關(guān)算法在低信噪比和較少快拍數(shù)下存在欠估計(jì)的問題，提出一種適用于空間平穩(wěn)噪聲下基于?1稀疏正則化的信源個數(shù)估計(jì)新算法。該算法利用信號協(xié)方差矩陣特征值分解得到的特征值序列的稀疏性，選取合適的正則化參數(shù)對信號源個數(shù)進(jìn)行估計(jì)。理論分析和仿真實(shí)驗(yàn)表明，所提算法可以在較低信噪比的空間平穩(wěn)噪聲條件下，實(shí)現(xiàn)對較少快拍數(shù)下陣列接收數(shù)據(jù)信源個數(shù)的精確估計(jì)。

稀疏正則化；信源個數(shù)估計(jì)；空間平穩(wěn)噪聲；正則化參數(shù)

1 引言

隨著陣列傳感器在雷達(dá)、聲納、無線通信和醫(yī)學(xué)成像等許多領(lǐng)域的廣泛使用[1]，陣列信號處理的重要性日益凸顯。精確的信源數(shù)是許多超分辨陣列信號處理算法實(shí)現(xiàn)的基礎(chǔ)，如果信源個數(shù)估計(jì)錯誤，這些算法的估計(jì)性能會顯著下降，甚至完全失效。

陣列信號中的信源個數(shù)最初是通過假設(shè)檢驗(yàn)方法來估計(jì)的，在空間平穩(wěn)白噪聲條件下，根據(jù)先驗(yàn)知識預(yù)設(shè)判決門限，此方法的缺點(diǎn)是帶有很強(qiáng)的主觀性。為解決這一問題，Wax和Kailath[2]首先將信息論準(zhǔn)則引入陣列信號信源個數(shù)估計(jì)中，該類方法中最具代表性且比較簡單易行的是根據(jù) Akaike信息論準(zhǔn)則(AIC, Akaike information criterion)[3]和最小描述長度(MDL, minimum description length)[4]準(zhǔn)則提出的信源數(shù)估計(jì)算法。為了進(jìn)一步提高抗噪能力，文獻(xiàn)[5]從算法的頑健性出發(fā)提出了一個比較穩(wěn)健的 MDL算法(robust-MDL)，文獻(xiàn)[6]則采用最大特征值變化率準(zhǔn)則(MEVRC, maximum eigenvalue varied rate criteria)對信源個數(shù)進(jìn)行估計(jì)。然而，上述的信號源個數(shù)估計(jì)方法均是利用白噪聲信號模型推導(dǎo)出來的，僅適用于白噪聲條件。但在實(shí)際中，由于各種因素的影響，白噪聲條件難以滿足。為此，文獻(xiàn)[7]提出了用Gerschgorin圓盤定理（GDE,Gerschgorin disk estimator）判斷信源個數(shù)的方法，可適用于有色噪聲條件，但其調(diào)整因子的選擇較為困難。另一方面，在低快拍數(shù)和低信噪比的情況下，上述算法信源個數(shù)估計(jì)的精度均顯著下降。

針對上述問題，本文將理想情況下信號協(xié)方差矩陣特征值分解得到的具有稀疏性的特征值（SREV,sparse representation of eigenvalues vectors）序列作為重構(gòu)目標(biāo)；同時利用協(xié)方差矩陣估計(jì)誤差的概率分布獲取重構(gòu)殘差項(xiàng)較大概率的置信上界，以此作為約束條件來最小化待求解矢量的?1范數(shù)，從而得到一種簡單易懂且較為準(zhǔn)確的參數(shù)選取方法，進(jìn)而提出了一種基于?1稀疏正則化[8,9]的陣列信號信源個數(shù)估計(jì)新算法(?1-SREV)。與現(xiàn)有的基于信息論準(zhǔn)則、基于蓋爾圓盤定理的信號源估算方法不同，本文是在稀疏表示理論框架內(nèi)研究信號源個數(shù)估計(jì)問題，結(jié)合稀疏表示能夠用較少的采樣數(shù)據(jù)重構(gòu)原信號的優(yōu)點(diǎn)，使本文算法具有不需精確已知陣列流形、適用于較低信噪比且較少快拍數(shù)條件、陣列信號個數(shù)估計(jì)頑健性較好等優(yōu)點(diǎn)。

2 信號模型

假設(shè)K個入射角為θi,i=1,2,…,K 的遠(yuǎn)場平穩(wěn)窄帶信號入射到由M(M＞K)個陣元組成的陣列天線上，則t時刻接收到的數(shù)據(jù)x(t)=[x1( t),…,xM(t )]T為

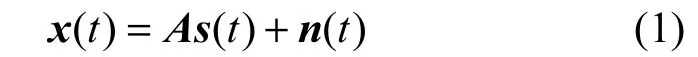
其中，X=[x(1),x(2),…,x(t),…]為陣列接收數(shù)據(jù)矩陣，S=[s(1),s(2),…,s(t),… ]為信號數(shù)據(jù)矩陣，N=[n(1),n(2),…,n(t),…]為噪聲數(shù)據(jù)矩陣。則陣列信號的協(xié)方差矩陣的表達(dá)式為

其中，U為特征矢量矩陣，V為由特征值組成的對角矩陣

式(5)中的特征值滿足如下關(guān)系

然而考慮實(shí)際情況，在有限快拍數(shù)的情況下，信號源個數(shù)估計(jì)受到較大影響，具體原因如下：設(shè)有限快拍數(shù)下，采樣協(xié)方差矩陣如式(7)所示。

其中，矩陣ΔR為誤差矩陣，文獻(xiàn)[10]表明其滿足下列漸進(jìn)高斯分布

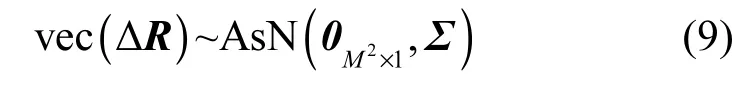
這里，vec(·)表示矩陣列向量化，AsN(μ, σ2)表示均值為μ，方差為σ2的漸近正態(tài)分布，Σ為協(xié)方差矩陣，L為快拍數(shù)，?表示 Kronecker積。由于計(jì)算誤差的影響，有限快拍數(shù)據(jù)下的陣列協(xié)方差矩陣的噪聲特征值不再相等，而是具有式(10)所示的關(guān)系。

將式(8)與式(2)做比較，可以看出誤差矩陣ΔR類似于信號模型中噪聲矩陣N的地位，結(jié)合式(3)對式(8)進(jìn)行修改，從而構(gòu)建相關(guān)域上模型，其表達(dá)式如式(11)所示，基于此模型本文提出了一種陣列信號信源個數(shù)估計(jì)新算法。

3 信源個數(shù)估計(jì)算法研究

3.1 算法原理

首先假設(shè)在無限快拍數(shù)，即式(6)成立的理想條件下，本文很自然地想到利用特征值分解后得到的最小特征值λM作為噪聲功率的估計(jì)，消除特征值序列中的噪聲功率，從而得到稀疏度為K的稀疏向量

則向量u中非零元素的個數(shù)便是信號源的個數(shù)。

然而，在有限陣列快拍數(shù)據(jù)下，由于噪聲的特性（如均值、方差）會有一定偏差，導(dǎo)致陣列信號協(xié)方差矩陣特征值分解得到的噪聲子空間不再相等，則利用上述方法得到的向量D如式(13)所示。

參考式(12)，本文的核心思想是利用稀疏表示相關(guān)算法，對稀疏向量u進(jìn)行重構(gòu)，進(jìn)而將信源個數(shù)估計(jì)轉(zhuǎn)化為向量的稀疏度K的求解，其稀疏度用?0范數(shù)表示為，從而得到信源個數(shù)估計(jì)的算法如下。

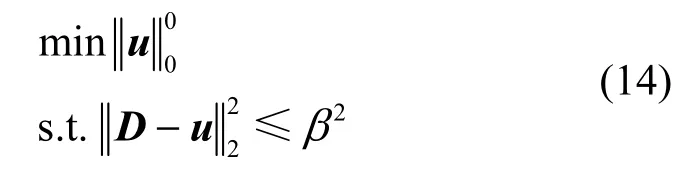
其中，β為“容噪”參數(shù)[9]，其具體選取方法將在下節(jié)中介紹。這里，向量u為稀疏的假設(shè)是必要的，因?yàn)槿绻麤]有此假設(shè)，則式(14)為病態(tài)問題。但是，式(14)需要列出u中所有非零項(xiàng)位置的種可能的線性組合，才能得到最優(yōu)解。因此，其數(shù)值計(jì)算極不穩(wěn)定且為NP難問題。針對此問題，學(xué)者們提出許多近似算法，其中包括貪婪逼近算法[10]、FOCUSS 算法[11]以及?1和?p松弛算法[12]等。基于上述理論基礎(chǔ)，本文提出了基于?1稀疏正則化的信源個數(shù)估計(jì)新算法，其目標(biāo)函數(shù)為

表1不同信噪比條件下的稀疏向量u

其中，γ為正則化參數(shù)，其具體選取將在下節(jié)中具體介紹。這里假設(shè)γ選取適當(dāng)，設(shè)定信源個數(shù)為3，陣列的陣元數(shù)目為 6，則在不同信噪比的空間平穩(wěn)白噪聲條件下，通過式(15)得到的稀疏向量u如表1所示。由此表可以看出，本文算法可以將低信噪比下混淆的信號子空間與噪聲子空間很好地分離開來，使噪聲子空間的功率近似為零，進(jìn)而將信源個數(shù)的估計(jì)轉(zhuǎn)化為稀疏向量u中的稀疏度的求取。

3.2 正則化參數(shù)選取

式(15)中的正則化參數(shù)γ是信源個數(shù)估計(jì)算法中的重要參數(shù)，它的選取是否適當(dāng)不僅影響算法的收斂性及收斂速度，而且決定所求得的解是否收斂于真實(shí)解。為此，本文采用L-curve法[13]對參數(shù)γ進(jìn)行遍歷搜索，將殘差項(xiàng)最小值作為參數(shù)γ的估計(jì)值，得到參數(shù)γ在0.5～0.6范圍內(nèi)。表2為此范圍的參數(shù)γ在不同信噪比下的正確檢測率，由此表可以看出，在0.5～0.6范圍內(nèi)參數(shù)γ越小，意味著對向量的稀疏性約束越弱，故更適合在低信噪比條件下進(jìn)行信源個數(shù)估計(jì)；但隨著信噪比的增高，向量的稀疏性隨之增強(qiáng)，故參數(shù)γ有所增大，準(zhǔn)確率也更高。雖然此方法相對繁瑣，但對于固定系統(tǒng)模型來說，參數(shù)γ的值是不變的，故可預(yù)先設(shè)定。

由于正則化參數(shù)γ的選取較為復(fù)雜，本文利用拉格朗日乘子法將式(15)的無約束優(yōu)化問題轉(zhuǎn)化為如(16)所示的約束優(yōu)化求解問題。

則將正則化參數(shù)γ的估計(jì)轉(zhuǎn)化為式(17)中相對簡單易懂的參數(shù)β的選取問題。由上節(jié)介紹可知，本文的目標(biāo)是構(gòu)建一個僅包含信號特征值的稀疏向量u，這意味著參數(shù)β的選取應(yīng)滿足：β足夠大，使?jié)M足的概率很小，這里。由本文第2節(jié)可知，向量n中的元素不為零是有限快拍數(shù)下誤差矩陣ΔR所引起的，由于vec(ΔR)是符合漸進(jìn)高斯分布[14]的，故可將向量n的方差近似看作服從自由度為M的χ2分布。根據(jù)分布情況，設(shè)定置信值p（通常情況下，為使式(16)對于陣列信號個數(shù)具有較好的頑健性，設(shè)置p=0.01），將上限值作為參數(shù)β的值。

表2正則化參數(shù)γ取值為范圍內(nèi)0.5～0.6不同信噪比下的估計(jì)準(zhǔn)確率

3.3 算法實(shí)現(xiàn)步驟

為了解決(16)中的?1稀疏正則化問題，本文使用斯坦福大學(xué)Grant和Boyd教授等開發(fā)的CVX工具箱對其進(jìn)行求解，信源個數(shù)估計(jì)的具體求解步驟如下所示。

?1-SREV 信源個數(shù)估計(jì)算法

已知∶ 陣列接收信號x(t)；陣元個數(shù)M；β2=(χ2(M))2

求解∶ 信源個數(shù)K

算法∶ 對陣列信號x(t)的協(xié)方差矩陣進(jìn)行特征值分解得到特征值序列Λ；

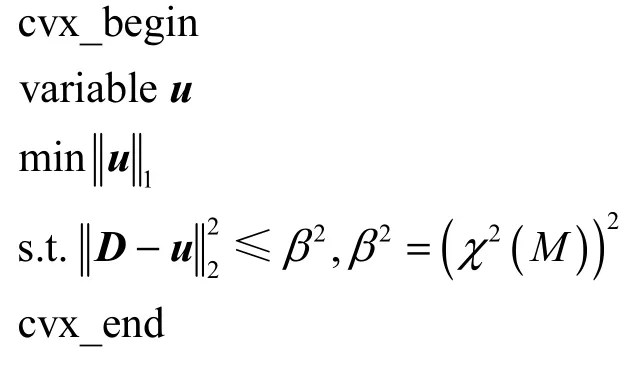
求取向量u的稀疏度作為信號源個數(shù)估計(jì)值。

本文通過分析算法所需的乘法次數(shù)估算運(yùn)算復(fù)雜度。以K個信號源的M維陣列為例，采用式(15)的信號源估計(jì)的運(yùn)算復(fù)雜度主要包括?1稀疏正則化目標(biāo)函數(shù)和特征值分解，為，采用式(16)的運(yùn)算復(fù)雜度則為O( K3M3)。而采用RMDL算法的運(yùn)算復(fù)雜度為O( M4)[5]。雖然本文算法在運(yùn)算復(fù)雜度上并沒有明顯改善，但是本文利用采樣協(xié)方差矩陣與理想自相關(guān)矩陣R存在計(jì)算誤差矩陣ΔR=?R滿足漸進(jìn)高斯分布vec(ΔR)～AsN(0M2×1,Σ)的原理，將其作為“容噪”參數(shù)β的選取依據(jù)，從而克服了有限快拍數(shù)所引起的誤差，估計(jì)的韌性更好，抗噪性能更強(qiáng)。同時結(jié)合稀疏表示能夠用較少的采樣數(shù)據(jù)重構(gòu)原信號的優(yōu)點(diǎn)，使本文算法更加適用于較少快拍數(shù)的條件。

4 仿真

為了說明上述算法的有效性，將本文提出的算法?1-SREV 與已有算法 RMDL[5]、AIC[3]、MEVRC[6]和 MGDE[7]進(jìn)行信號源個數(shù)估計(jì)實(shí)驗(yàn)比較，其中，MGDE算法調(diào)整因子經(jīng)多次實(shí)驗(yàn)取0.1。本文設(shè)定實(shí)驗(yàn)條件為 10陣元，間距為半波長的均勻圓陣，接收信號為3個遠(yuǎn)場獨(dú)立源，其入射角分別為(40°，60°，80°)，Monte Carlo 實(shí)驗(yàn)次數(shù)為 200。衡量算法性能的指標(biāo)選為估計(jì)準(zhǔn)確率 Pd，其定義為正確估計(jì)次數(shù)與 Monte Carlo實(shí)驗(yàn)次數(shù)的比值。

4.1 不同信噪比下，信源個數(shù)估計(jì)算法性能對比分析

本文在空間平穩(wěn)噪聲條件下，快拍數(shù)為 50時，對上述5種算法的信源個數(shù)估計(jì)性能進(jìn)行比較分析。圖 1為平穩(wěn)噪聲條件下，5種算法信源個數(shù)估計(jì)準(zhǔn)確率 Pd隨SNR變化曲線仿真。由此圖可以看出，當(dāng)信噪比較低(SNR≤?4dB )時，相對于其他3種方法，AIC算法和本文算法估計(jì)性能較好，且AIC算法準(zhǔn)確率要高于本文算法；隨著信噪比的增加(?4dB＜SNR ＜?2dB )，本文算法性能迅速提高，但AIC算法改善不明顯；隨著SNR進(jìn)一步增加(SNR≥2 dB )，本文算法和其他算法均達(dá)到 100%估計(jì)準(zhǔn)確率，但 AIC算法對信源個數(shù)準(zhǔn)確率仍無法達(dá)到100%，從而影響后續(xù)基于信源個數(shù)相關(guān)陣元信號處理算法的頑健性。綜上考慮，相對于其他算法，本文算法具有更好的綜合性能。

圖1平穩(wěn)噪聲條件下，對應(yīng)于SNR的算法性能比較

雖然本文算法是白噪聲假設(shè)下提出的，但當(dāng)噪聲為色噪聲時（實(shí)驗(yàn)中的色噪聲是白噪聲經(jīng)過濾波裁剪得到的），在參數(shù)β預(yù)先設(shè)定好的情況下，同樣具有較好的結(jié)果。由文獻(xiàn)[15]可知，RMDL、AIC、MEVRC和EDC的估計(jì)算法都是基于白噪聲信號模型推導(dǎo)出來的，無法準(zhǔn)確估計(jì)此時的信源數(shù)。MGDE算法雖然可以處理，但是當(dāng)MGDE進(jìn)行酉變換時，其陣列協(xié)方差矩陣較小特征值對應(yīng)的特征向量與導(dǎo)向矢量并不是完全正交的，所以在信噪比較高的情況下，其估計(jì)的誤差也不會趨于零。圖2為色噪聲條件下，信源個數(shù)估計(jì)準(zhǔn)確率對應(yīng)于SNR的算法性能對比，可以看出，本文提出的 ?1-SRAE 算法，相對于MGDE算法受色噪聲的影響更小。

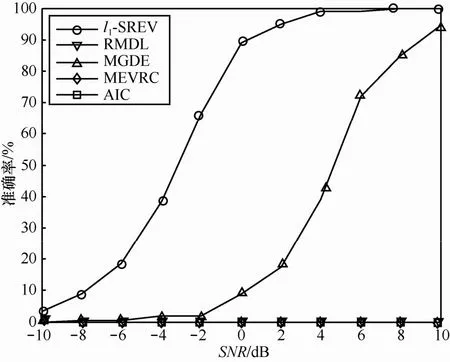
圖2色噪聲條件下，對應(yīng)于SNR的算法性能比較

4.2 不同快拍數(shù)下，信號源個數(shù)估計(jì)算法性能對比分析

圖3是5種算法在信噪比為0 dB的平穩(wěn)噪聲條件下，快拍數(shù)的變化從10到240時算法的估計(jì)性能比較仿真。從圖中可以看出，在較少快拍數(shù)（快拍數(shù)小于10）的條件下，AIC算法的估計(jì)精度相對較高，其他各算法的估計(jì)準(zhǔn)確率均不高。但隨著快拍數(shù)的增加，由于本文算法較好地克服了有限快拍所引起的誤差，估計(jì)準(zhǔn)確率迅速提升。當(dāng)快拍數(shù)增加到50時，估計(jì)準(zhǔn)確率便達(dá)到了100%，RMDL算法則在快拍數(shù)為70時，才達(dá)到100%的估計(jì)準(zhǔn)確率，而其他算法則在快拍數(shù)增加到200時，仍無法達(dá)到100%的估計(jì)準(zhǔn)確率。綜上可以看出，本文算法可以在較少快拍數(shù)下實(shí)現(xiàn)對信源個數(shù)的精確估計(jì)。

圖3不同快拍數(shù)下，不同算法信源個數(shù)估計(jì)準(zhǔn)確率對比

5 結(jié)束語

精確的信源數(shù)是許多超分辨陣列信號處理算法實(shí)現(xiàn)的基礎(chǔ)。針對現(xiàn)有的信號源個數(shù)估計(jì)算法在低信噪比和低快拍數(shù)下估計(jì)性能差的問題，本文提出了一種適用于遠(yuǎn)場陣列信號的基于?1稀疏正則化的信源個數(shù)估計(jì)新算法，理論和仿真實(shí)驗(yàn)證明了該算法在低快怕數(shù)和低信噪比的情況下，與現(xiàn)有信號源個數(shù)估計(jì)算法相比具有較好的一致性和頑健性。

[1]程偉, 左繼章. 基于時空結(jié)構(gòu)的陣列信號三維參數(shù)同時估計(jì)方法[J].通信學(xué)報(bào), 2004, 25(10): 67-74.CHENG W, ZUO J Z. A new method for simultaneous estimation of 3-D parameters of array signal based on time-space structure[J]. Journal on Communications, 2004, 25(10): 67-74.

[2]CHEN W, WONG K M, REILLY J P. Detection of the number of signals: a predicted eigen-threshold approach[J]. IEEE Transactions on Signal Processing, 1991, 39(5): 1088-1098.

[3]ZHAO L C, KRISHNAIAH P, BAI Z D. Remarks on certain criteria for detection of number of signals[J]. IEEE Transactions on Acoustics,Speech and Signal Processing, 1987, 35(2): 129-132.

[4]WAX M, ZISKIND I. Detection of the number of coherent signals by the MDL principle[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1989, 37(8): 1190-1196.

[5]FISHLER E, POOR H V. Estimation of the number of sources in unbalanced arrays via information theoretic criteria[J]. IEEE Transactions on Signal Processing, 2005, 53(9): 3543-3553.

[6]LIU Y, SORAGHAN J, DURRANI T. Detection of number of harmonics by maximum eigenvalue varied rate criteria[C]//International Conference on Acoustics, Speech, and Signal Processing (ICASSP).1990: 2543-2546.

[7]WU H T, YANG J F, CHEN F K. Source number estimators using transformed Gerschgorin radii[J]. IEEE Transactions on Signal Processing, 1995, 43(6): 1325-1333.

[8]石光明, 劉丹華, 高大化. 壓縮感知理論及其研究進(jìn)展[J]. 電子學(xué)報(bào), 2009, 37(5): 1070-1081.SHI G M, LIU D H, GAO D H. Advances in theory and application of compressed sensing[J]. Chinese Journal of Electronics, 2009, 37(5):1070-1081.

[9]MALIOUTOV D, ?ETIN M, WILLSKY A S. A sparse signal reconstruction perspective for source localization with sensor arrays[J].IEEE Transactions on Signal Processing, 2005, 53(8): 3010-3022.

[10]RAO B D, ENGAN K, COTTER S F. Subset selection in noise based on diversity measure minimization[J]. IEEE Transactions on Signal Processing, 2003, 51(3): 760-770.

[11]OTTERSTEN B, STOICA P, ROY R. Covariance matching estimation techniques for array signal processing applications[J]. Digital Signal Processing, 1998, 8(3): 185-210.

[12]MILLER A. Subset selection in regression[M]. CRC Press, 2002.

[13]YARDIBI T, LI J, STOICA P. Source localization and sensing: a nonparametric iterative adaptive approach based on weighted least squares[J]. IEEE Transactions on Aerospace and Electronic Systems,2010, 46(1): 425-443.

[14]CANDES E, RUDELSON M, TAO T, et al. Error correction via linear programming[C]//IEEE Symposium on.Foundations of Computer Science (FOCS). 2005: 668-681.

[15]CHEN W G, REILLY J P, WONG K M. Detection of the number of signals in noise with unknown, non-white covariance matrices[C]//IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP). 1992, 5: 377-380.

New source number estimation algorithm based on ?1sparse regularization

JIN Fang-xiao1, QIU Tian-shuang1, WANG Peng1, XIA Nan2, LI Jing-chun2
( 1.Faculty of Electronic Information and Electrical Engineering, Dalian University of Technology, Dalian 116024, China;2.State Radio Monitoring Center, Beijing 100037, China)

In view of the problems of inefficient in low SNR and less snapshots when using existing sources number estimation related algorithms, a new algorithm based on ?1sparse regularization under space stationary noise was proposed to estimate the number of signal sources. The algorithm estimated the sources number by using the sparse representation of eigenvalues vectors with the suitable regularization parameter. Theoretical analysis and simulation results show that the algorithm can realize an accurate sources number estimation in low SNR and less snapshots.

sparse regularization, sources number estimation, space stationary noise, regularization parameter

s:The National Natural Science Foundation of China (No.61139001, No.61172108, No.81241059, No.61501301),The National Key Technology Ramp;D Program (No.2012BAJ18B06-04)

TN911. 7

A

10.11959/j.issn.1000-436x.2016198

2016-02-02；

2016-08-30

邱天爽，qiutsh@dlut.edu.cn

國家自然科學(xué)基金資助項(xiàng)目（No.61139001, No.61172108, No.81241059, No.61501301）；國家科技支撐計(jì)劃基金資助項(xiàng)目（No.2012BAJ18B06-04）

金芳曉（1988-），女，遼寧沈陽人，大連理工大學(xué)博士生，主要研究方向?yàn)槔走_(dá)信號處理、無線電信號處理和陣列信號處理。

邱天爽（1954-），男，江蘇海門人，博士，大連理工大學(xué)教授、博士生導(dǎo)師，主要研究方向?yàn)榻y(tǒng)計(jì)信號處理、射頻與通信信號處理等。

王鵬（1989-），男，河北寧晉人，大連理工大學(xué)博士生，主要研究方向?yàn)槔走_(dá)信號處理、無線電信號處理和陣列信號處理。

夏楠（1983-），男，遼寧大連人，博士，國家無線電監(jiān)測中心高級工程師，主要研究方向?yàn)橥ㄐ判盘柋O(jiān)測與信息處理等。

李景春（1966-），男，河北寧晉人，博士，國家無線電監(jiān)測中心副主任兼總工程師，主要研究方向?yàn)闊o線電監(jiān)測理論與應(yīng)用等。