直線電動機伺服系統精確自動建模方法研究

柳 瑞，張 馳，沈林勇，趙 飛，董 良，李 榮

(1.上海大學，上海 200072；2.中國科學院 寧波工業技術研究院，寧波 315201)

?

直線電動機伺服系統精確自動建模方法研究

柳 瑞1,2，張 馳2，沈林勇1，趙 飛2，董 良1,2，李 榮2

(1.上海大學，上海 200072；2.中國科學院 寧波工業技術研究院，寧波 315201)

永磁同步直線電動機伺服系統具有復雜耦合性、部件參數測量難度大、不確定等特點，使理論與真實模型存在差異。頻域特性直觀反映系統的響應和運動性能，快速自動頻域模型辨識具有重要意義。在dSPACE/MATLAB實驗平臺上產生正弦掃頻信號，簡便靈活。對比對數掃頻實驗與穩態步進逐點掃描實驗曲線，結果表明對數掃頻可以快速精確地獲得頻域特性。采用最小二乘綜合零極點自動優化配置的方法擬合模型，實現快速準確建模。

永磁同步直線電動機；正弦掃頻；頻域特性；自動建模

0 引 言

目前，永磁同步直線電動機伺服系統在精密機床、電子制造等領域得到了廣泛應用。伺服系統的控制性能決定著系統加工性能和效率[1]，為提高伺服系統控制性能就需要明確被控對象精確模型。磁場矢量控制實現電流穩態解耦，基于矢量控制建立永磁同步直線電動機模型是常用建模方法[2]，然而永磁同步直線電動機伺服系統具有復雜耦合性和各部件參數測量難度大、不精確等特點，基于理論模型與真實模型具有一定差異[3]。因此，通過系統響應辨識方法，獲得實際系統模型具有現實意義，是進行控制器設計實現良好控制性能的基礎[4-8]。

在工業應用領域中(如振動分析和伺服系統辨識)常采用頻率辨識的方法，直接辨識系統的傳遞函數。實驗室中常用正弦激勵、隨機激勵和錘擊法測量系統頻響函數，正弦激勵常用于航天航空模型的測試，具有相當可靠性[9]。

正弦掃頻試驗有正弦逐點掃描試驗和瞬時頻率變化掃頻試驗。前者是一種穩態正弦掃頻，需滿足系統在每一個頻率點處都進入穩定狀態，充分暴露系統特性，得到非常高精度的頻響函數，但每次改變頻率后需等待系統瞬態響應結束，比較耗時，并且較長時間的振動對系統容易造成損壞。

近幾年隨硬件發展，瞬時頻率變化掃頻試驗得以發展，如Chirp信號掃頻[10]和正弦掃頻，縮短了掃頻試驗時間，并可以更加真實地模擬產品的工作環境[11]。Gloth[12]對逐點正弦激勵、多點組合正弦激勵、隨機激勵和掃頻激勵進行研究，使用慢掃頻信號作為激勵，既提供較大的推動力，又節省測試時間。文獻[13]中通過設計正弦掃頻的產生和綜合分析，解決掃頻信號的非穩態問題。針對直線電動機伺服系統非線性、小阻尼特性，合理選擇掃頻激勵信號可提高系統辨識精度和節約測試時間[14]。

本文首先分析正弦掃頻頻域特性的測試原理，基于dSPACE/MATLAB半實物仿真實驗平臺實現掃頻信號的生成和數據采樣、處理，可替代價格昂貴的傳統的頻率特性測試儀和信號發生器，具有簡便靈活、節約成本的優點。對于高速電機輕阻尼結構，研究掃頻速率對系統的影響，用來選擇最佳掃頻速率；并進行正弦步進逐點掃頻實驗，對比驗證正弦掃頻測試系統頻域特性的可靠性和快速性。采用最小二乘及零極點自動優化配置的模型擬合方法，實現快速準確建模。

1 正弦掃頻激勵頻域特性測試原理

永磁同步直線電動機伺服驅動系統由運動控制器、驅動器、直線電動機、線性導軌、直線光柵、工作臺等部件組成。基于dSPACE/MATLAB控制實驗平臺產生測試信號，編程方便，實時采集數據，可替代價格昂貴的傳統的頻率特性測試儀和信號發生器，便捷靈活，節約成本[15-17]。該系統模型辨識原理框圖如圖1所示，DS1103單板I/O模塊DAC端口輸出掃頻激勵信號，編碼器端口連接電機位置光柵端口。ControlDesk實現實時測試界面，進行數據的采集和記錄，將數據導入MATLAB中進行處理、分析和自動模型擬合，快速得到系統較精確數學模型。實際的辨識對象包括直線電動機、驅動器(電流環控制、濾波等)等，驅動器內部采用PI控制。

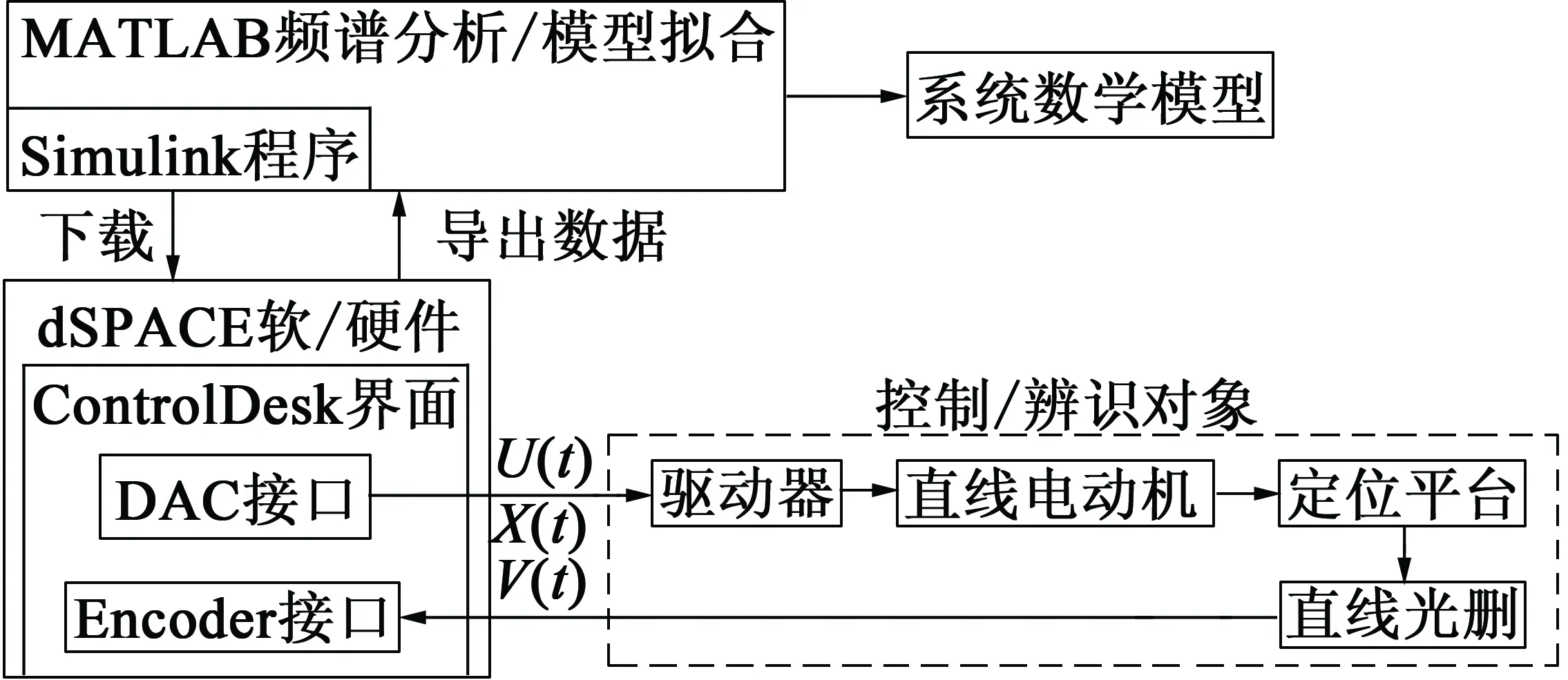
圖1 永磁同步直線電動機系統模型辨識原理框圖

1.1 正弦掃頻信號

正弦掃頻函數精確表達式：

(1)

式中：A(t)為幅值，一般為常數；φ0為初相位。根據頻率的變化規律，可分為線性掃頻和對數掃頻。對比對數掃頻與線性掃頻頻率變化特性，在低頻時對數掃頻頻率變化較慢，頻率間隔較小，更適合掃頻實驗。對數掃頻頻率表達式:

(2)

式中：f0為起始頻率；r為掃頻速率,表示每分鐘r個倍頻程(oct/min)。 c和φ0組成新相位值，對數掃頻函數精確表達式：

(3)

基于以上推導，該信號在dSPACE/MATLAB控制實驗平臺上通過編輯Simulink程序實現。對數頻率變化在掃頻速率較低時，一個周期內頻譜可認為單一譜線。針對實驗選用的掃頻速率，對數掃頻信號25Hz處相鄰兩周期頻率分別為25.368Hz和25.381Hz，前后周期頻率相差甚小，可認為頻率連續變化。

1.2 數據相關分析

實驗采集得到的數據是時域數據，需將數據變換為頻域數據。由于FFT分析整周期信號無泄漏，針對慢掃頻信號頻率連續變化，計算方便[18]。相關分析抑制噪聲效果很好，步進逐點掃頻用相關分析法可提高辨識精度[19]。

首先需要對時域測試數據進行預處理，數據預處理主要包括對高頻噪聲的濾波、粗大誤差的剔除和穩態截取。由于速度信號是由位置值微分得到，慢掃頻信號中主要存在差分時的高頻噪聲，對時域數據進行滑動平均濾波效果較好，計算簡便。步進逐點掃頻需得到系統穩態響應，當存在某些異常和響應非穩定時的數據需要剔除。對預處理后數據進行FFT譜分析和相關分析，FFT譜分析利用MATLAB計算簡單方便；相關分析在實驗平臺實現原理如下。

設頻率為f0的單位輸入信號xi(t)，采集信號長度為N，采樣間隔為Δt，待辨識系統響應：

(4)

式中：Af0為待識別信號幅值，φf0表示相位。分別計算yi(t)與單位信號sin(2πf0·iΔt)和cos(2πf0·iΔt)的相關函數：

(5)

由此得到正弦函數穩態響應的幅值和相位，即待辨識系統的幅相特性分別：

(6)

2 快速自動建模方法

由于該測試系統采用速度環開環系統，在低頻段呈近似線性特性，利用最小二乘方法擬合模型，計算簡便可靠。隨著ω的增大，使得最小二乘擬合B(jω)增大，擬合誤差增加[20]，故在中高頻段通過獲取頻率曲線零極點并調整模態參數進行曲線擬合，即在頻率特性曲線峰值處設置阻尼合適的極點，在波谷處設置相應零點，分別進行配置。對于更高頻段，受各種不確定性影響較大，采用適當增益覆蓋曲線，便可得到整個頻段精確模型，同時含有未建模動態不確定性的模型，便于魯棒控制設計，提高系統魯棒性。

2.1自動查找系統零極點

由于在不同頻段采用不同的建模方法，因此，需要合理劃分低高頻率段，并確定系統的零極點。在頻率特性中含頻率、增益和相位信息，通過對增益數據列的迭代比較找出曲線的轉折點，即曲線極值點，同時也可能是系統零極點。考慮模態組合及測試誤差，曲線不是嚴格意義上的單調光滑曲線，存在許多毛刺，增加了查找正確零極點的難度。

圖2 確定曲線極大點原理框圖

設置增益分辨率ΔMag已消除曲線毛刺的影響，其中以極大值點為例，自動查找程序原理如圖2所示。為得到系統主要零極點，設頻率分辨率ΔFreq范圍內含有兩個或多個相鄰極大(或極小)點時，取極值最大(或最小)的一個作為系統零極點記錄保存。該系統零極點如圖 3所示，最終取頻率最小的極點(或零點)的頻率作為低頻率段臨界頻率。

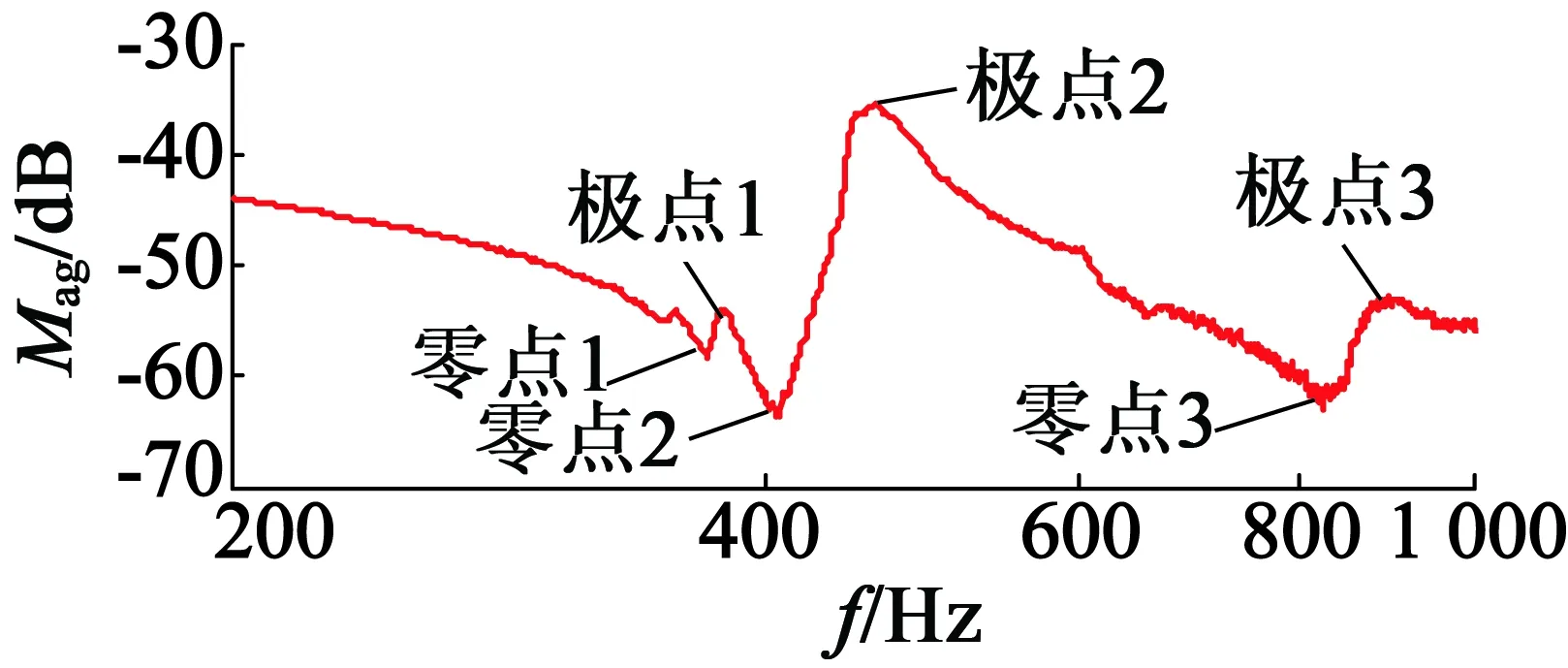
圖3 自動查找系統零極點

2.2 低頻段最小二乘擬合

最小二乘計算簡便可靠，設系統傳遞函數：

(7)

在任意某個頻率點處，極小化誤差目標函數：

(8)

可得到擬合參數：

(9)

圖4為對頻率特性低頻段擬合。可見低頻段擬合精度較高。

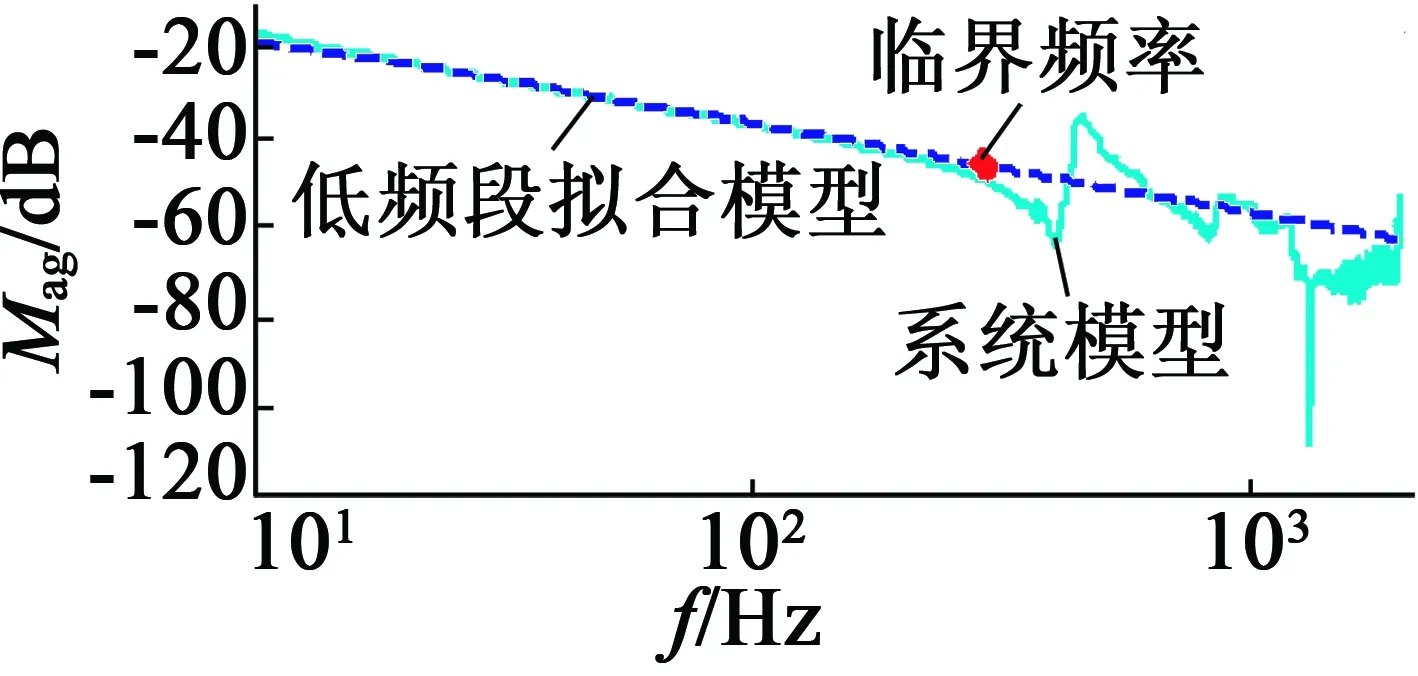
圖4 低頻段模型

2.3 中高頻段零極點配置自動建模

快速自動擬合曲線實現原理圖如圖5所示，通過自動求取合適的阻尼比ξ，使該頻率段曲線的擬合誤差小于很小的正常數，即確保擬合誤差在一定范圍內。

圖5 配置零極點的自動擬合原理圖

當ωn確定時，阻尼比ξ的大小決定著幅值增益，ξ越大幅值增益越小。依據此規律，以Δξ為其分辨率來改變ξ的大小，直到擬合誤差滿足要求。實驗中各零極點頻率值和阻尼比值如表1所示。頻率值為圖3中得到的各個零極點的頻率，阻尼比為自動擬合值。

表1 系統調整后各點的阻尼比

3 實 驗

實驗選用辨識對象為自主研發的XY平臺的X軸永磁同步直線電動機和CopleyXenus型驅動器，Copley驅動器設置為電流環差分模擬輸入模式，設計電機參數和驅動器參數設置如表2所示，位置傳感器為美國MicroE的MercuryⅡ型直線光柵尺。整體實驗裝置如圖 6所示。

系統頻率特性直觀反映系統的響應速度、精度和運動平穩性。為直觀顯示系統理論模型與實際模型的差異，建立經典控制方法的理論模型。根據矢量控制的基本原理，對永磁同步直線電動機的電壓方程、電磁推力方程和機械運動方程簡化得到理論數學模型，仿真其頻域特性如圖7虛線所示。圖7實線為實驗得到系統頻域特性，存在振動模態，經分析，中頻段主要振動是有機械支撐結構引起；中高頻段引起振動原因較為復雜。可見，理論模型不能反映實際驅動器部件特性和動子(或工作臺)支撐結構的機械特性，故實際系統辨識很有必要，具有現實意義，是控制器設計的基礎。

圖6 基于ds1103的參數辨識實驗臺

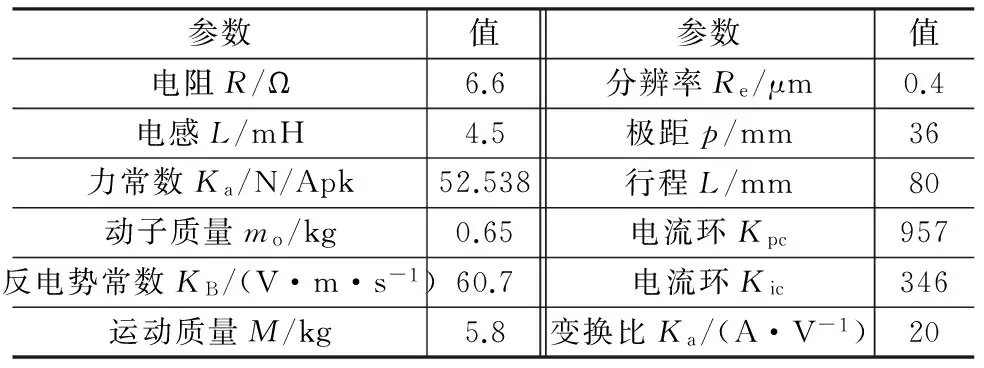
參數值參數值電阻R/Ω6.6分辨率Re/μm0.4電感L/mH4.5極距p/mm36力常數Ka/N/Apk52.538行程L/mm80動子質量mo/kg0.65電流環Kpc957反電勢常數KB/(V·m·s-1)60.7電流環Kic346運動質量M/kg5.8變換比Ka/(A·V-1)20

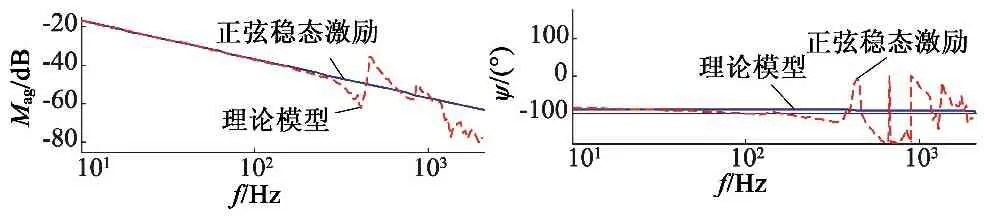
圖7 系統理論模型和實際模型頻域特性

在對數掃頻試驗中，掃頻速率過大使得系統響應幅頻特性峰值降低；速率過小時，由于速度信號是通過位置差分得到，使得測量噪聲較大，會降低系統信噪比。選用不同的頻率變化速率進行測試，綜合評比峰值幅值和高頻噪聲影響，最終確定合適激勵信號頻率變化速率為1.32 oct/min，分別對實際系統進行正弦掃頻和步進穩態掃頻實驗。系統實驗結果如圖 8所示，虛線是正弦穩態激勵下的測試結果，由于系統響應在穩定條件下測得，可作為實際系統理想頻率曲線；實線是對數掃頻激勵下測得的頻域特性。對比實驗結果，永磁同步直線電動機伺服系統正弦掃頻激勵方法具有相當可靠性和高效性。該伺服系統一階共振頻率在465 Hz附近。

圖8 實際系統掃頻激勵和步進穩態激勵下頻率特性

對掃頻激勵頻率特性曲線使用最小二乘綜合自動零極點配置進行擬合，擬合結果如圖 9所示，低頻段幅頻特性盡量貼近實際曲線，絕對誤差<0.5 dB，中高頻段擬合模型的幅值頻率特性曲線高于實際曲線，這樣控制器設計時，就會加強對該頻率振動的抑制，提高系統的魯棒性；零極點處擬合絕對誤差在3 dB左右，保證足夠的幅值裕量的同時減小模型的相位損失。擬合模型與實際模型的誤差符合建模要求。由于實際系統具有一定延時，為方便控制器設計，綜合低頻段與中高頻段模型，得到8階的系統模型傳遞函數表達式如式(9)，實現快速建模。

Gsys=(-13s7+1.202×105s6-4.077×108s5+

4.847×1012s4-2.542×1015s3+

4.542×1019s2-3.27×1021s+

1.227×1026)/(s8+1.122×104s7+

5.834×107s6+4.867×1011s5+

7.516×1014s4+5.104×1018s3+

2.764×1021s2+1.525×1025s+

該模型包含實際系統的未建模動態的不確定模型，為更好地實現系統的魯棒控制提高魯棒性提供了模型基礎。

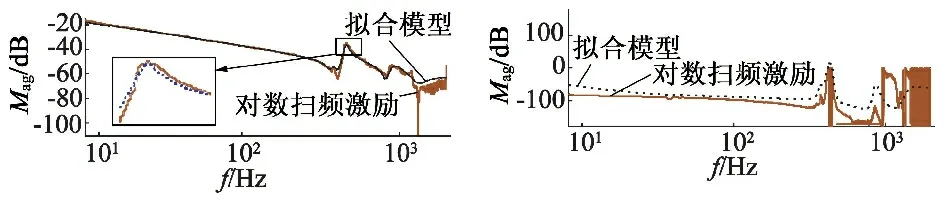
圖9 頻域特性系統模型擬合曲線

4 結 語

該辨識系統實驗平臺在dSPACE/MATLAB控制實驗平臺上實現，方便實現激勵信號和響應數據的采樣和處理，可替代傳統的頻率特性測試儀和信號發生器，便捷靈活，節約成本。推導對數掃頻函數的精確描述，為準確快速獲得實際伺服系統頻率特性提供理論依據，減小較長時間的振動對系統的損壞。對實際系統最小二乘綜合零極點自動優化配置擬合模型，快速實現準確建模，得到系統未建模不確定性模型，彌補理論模型的不足，并且自動保存零極點有利于控制器設計。

[1] 曹宇.伺服系統特性測試平臺設計[D].武漢：華中科技大學,2013.

[2] 田艷豐.永磁直線同步電動機魯棒控制策略研究[D].沈陽：沈陽工業大學,2010.

[3] 陳昊,王永,周建亮,凌杰.永磁同步電動機系統模型辨識[J].微特電機,2013,41(1):7-10.

[4] 張剛,劉品寬,張波,等.直線電機精密運動平臺軌跡跟蹤控制器設計[J].光學精密工程,2013,21(2):371-379.

[5] 陳正.基于非線性和柔性特性分析及補償的直線電機精密運動控制[D].杭州：浙江大學,2012.

[6] CHEN Z,YAO B,WANG Q.Adaptive robust precision motion control of linear motors with high frequency flexible modes[C]//the IEEE 12th Int.Workshop Adv.Motion Control,Sarajevo,Bosnia and Herzegovina,2012.[7] CHEN Z,YAO B,WANG Q.Accurate motion control of linear motors with adaptive robust compensation of nonlinear electromagnetic field effect[J].IEEE/ASME Trans.Mechatron.,2013,18(3):1122-1129.

[8] CHEN Z,YAO B,WANG Q.Adaptive robust precision motion control of linear motors with integrated compensation of nonlinearities and bearing flexible modes[J].IEEE Trans.Ind.Informat.,2013,9(2):965-973.

[9] 譚志紅.伺服控制系統的頻域辨識及激勵信號的研究[D].哈爾濱:哈爾濱工業大學,2010.

[10] 汪首坤,王軍政.基于調頻脈沖掃頻的導彈舵機頻率特性測試方法[J].北京理工大學學報,2006,26(8):697-699,703.

[11] 王帥,陳濤,李洪文,王建立. 光電跟蹤伺服系統的頻率特性測試與模型辨識[J]. 光學精密工程,2009,17(1):78-84.

[12] GLOTH G,SINAPIUS M.Analysis of swept-sine runs during modal identification[J].Mechanical Systems and Signal Processing,2004,18(6):1421-1441.

[13] 楊志東,叢大成,韓俊偉,等.正弦掃頻振動控制中的信號綜合與信號分析[J].振動工程學報,2008,21(3):309-313.

[14] GLOTH G,SINAPIUS M.Influence and characterization of weak non-linearities in swept-sine modal testing[J].Aerospace Science and Technology,2004,8(2):111-120.

[15] 張桅,趙剡,張寅.基于dSPACE的頻率特性測試與模型辨識研究[J].宇航計測技術,2010,30(1):57-60.

[16] 郎寶華,楊建華,李榕.基于dSPACE的電機控制系統實驗平臺研究[J].現代電子技術，2010,33(17):130-132.

[17] 陳鵬展,唐小琦,李銀剛.基于dSPACE的伺服控制模型實時仿真研究[J].微特電機，2008,36(9):25-27.

[18] 嚴俠,李曉琳,胡勇.運用正弦掃頻實現電動振動臺模型的頻域辨識[J].裝備環境工程,2015,(2):44-48.

[19] 陳連華,趙娜,王奕博,等.一種快速單步的頻率特性測試方法[J].電子測量技術,2011,(2):77-79，101.

[20] ABDULLAH A，MAMUN T H,LEE T S.Low frequency domain identification of transfer function model of a disk drive actuator[J].Mechatronics,2002,12(4):563-574.

Linear Motor Servo System Precision Automatically Model Methed Research

LIURui1,2,ZHANGChi2,SHENLin-yong1,ZHAOFei2,DONGLiang1,2,LIRong2

(1.Shanghai University, Shanghai 200072, China;2.Ningbo Institute of Industrial Technology, CAS, Ningbo 315201, China)

Some characteristics of permanent magnet synchronous linear motor (PMSLM) like complex coupling, difficult measurement of parameter and uncertain parameters have resulted in the difference between the theoretical model and the actual one. Automatic and rapid model identification is of great significance as its frequency domain characteristics directly reflect the response and performance of the system. Different types of sine-sweep signals based on dSPACE/MATLAB platform were generated and tested. The frequency response curves generated by logarithmic sweep and stepped sweep were compared. The experimental results show that logarithmic sweep is a better option for acquiring frequency response quickly and accurately. Curve fitting with least squares method in low frequency range and automatic zero-pole optimized configuration in middle and high frequency range were implemented to fit the frequency response curve and tune the model. The results validate that the proposed modeling approach is a fast and accurate way.

PMSLM; sine frequency sweep; frequency domain characteristics; automatically model

2015-11-17

國家自然科學基金項目(51207158)；寧波市重大攻關項目(2013B10045)；國家科技支撐計劃項目(2014BAF10B00)；中國科學院百人計劃項目(Y30901W407)

TM359.4

A

1004-7018(2016)04-0009-04

柳瑞(1989-)，女，碩士研究生，研究方向為伺服驅動系統控制及振動抑制研究。