科學史上對天體運行的認知過程

韋松英

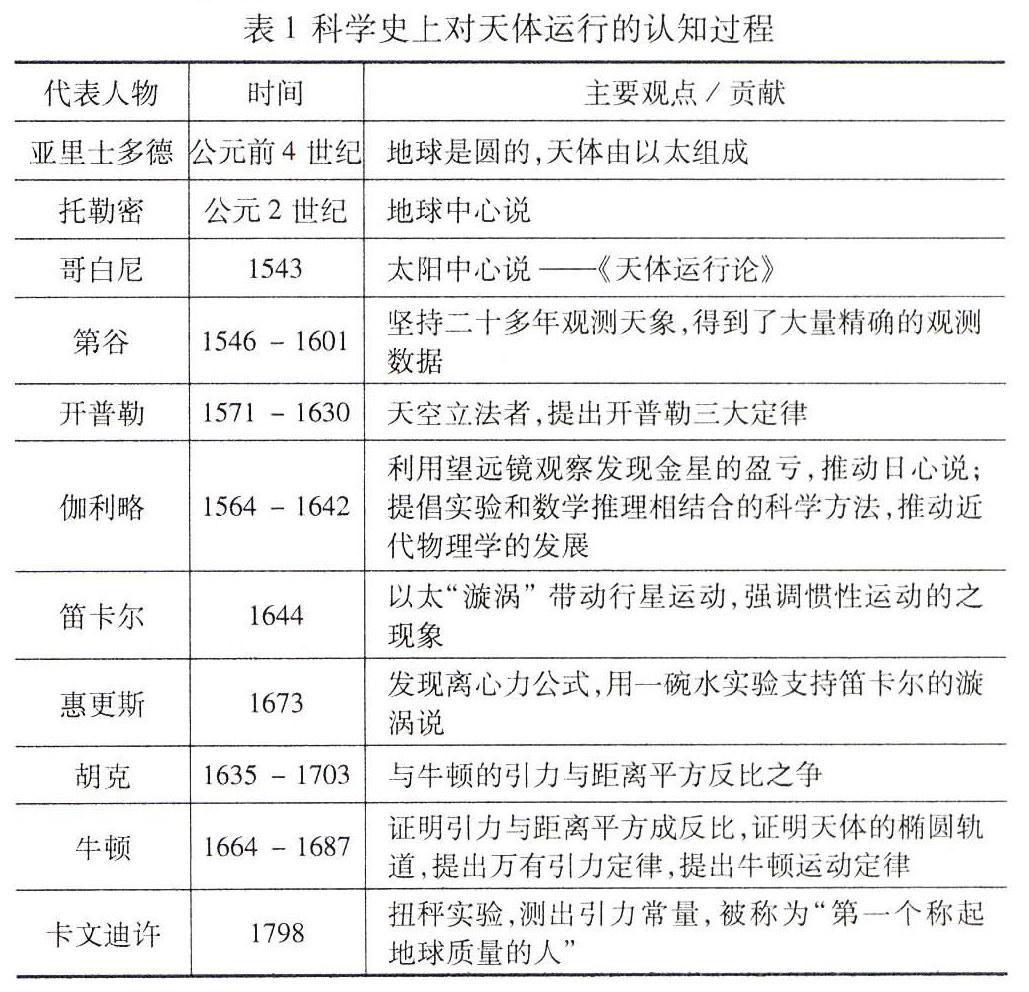
人類關于天體的運動的認識經(jīng)歷了漫長的過程，從提出地球是一個球，到證實地球是一球形；從地心說到日心說；從行星運動的圓軌道到橢圓軌道；從提出行星間存在引力到引力平方反比關系的猜想、證明，再到萬有引力定律的建立，經(jīng)歷了兩千多年的歷史。在這個過程中，無數(shù)科學家做出了努力，下面就按歷史發(fā)展的順序，對主要貢獻的歷史人物以及事件做一個綜述。

1“地心說”與“日心說”之爭

古時人們就有“天圓地方”的說法，認為地球是方形的。公元前五六世紀，畢達哥拉斯從哲學的角度，提出地球應是完美的圓形。

公元前350年前后，亞里士多德（前384-前322）觀察月食，認為那是地球在月球上的投影，據(jù)此推斷出地球應為球形。支持這一觀點的還有其他證據(jù)，比如觀察到遠處漸漸靠近的船只，總是先見到桅桿，后見到船身。亞里士多德還提出了地球是宇宙的中心，地球是由水、氣、火、土組成，天體由“以太”組成。

托勒密，地球中心說。地球是一個在宇宙中心一動不動的球體，太陽、月亮以及其他行星都圍繞著地球做完美的圓周運動。他提出，各行星都有自己的一個圓軌道，稱為“本輪”，所有本輪的圓心又在一個以地球為中心的圓周上，這個圓周稱為“均輪”。為了很好的解釋天體的運動，本輪均輪達到80多個，后來又提出了偏心圓，這個結(jié)構非常復雜，但卻較好的解釋了人們所能觀測到的天體的運動情況。他的這個天體模型一直流行到文藝復興結(jié)束。

哥白尼（1473-1543），他在意大利讀書時期，便對天文問題產(chǎn)生濃厚興趣。在學習托勒密的《至大論》后，他認為托勒密的體系太過復雜，他提出如果將太陽作為宇宙的中心，可以大大簡化托勒密的模型。1543年，哥白尼的著作《天體運行論》出版，他的體系將圓減少到了34個，與托勒密的體系相比，更為簡潔。但是在行星方位的預測方面，與托勒密相比，并沒有提高精度。

2行星運動軌道的確定

第谷（1546-1601），他在大學學習的是法律，但卻對天文學有著更為濃厚的興趣。他利用課余時間觀察天象，發(fā)現(xiàn)自己觀察到木星和土星靠在一起的時間比星歷表的預言早了一個月，這激勵他編制更為精確的星歷表。為了能有更好的觀察條件，他在歐洲游學，后來得到了丹麥國王的資助。1576年在赫芬島，胡恩島上建立天文臺、圖書館、實驗室、印刷廠。在那里觀察了二十多年，得到大量的天文數(shù)據(jù)。1599年，在丹麥國王腓特烈二世逝世后，移居布拉格，繼續(xù)觀察。他為后人留下了珍貴的、精確的觀測數(shù)據(jù)，為開普勒后續(xù)研究提供了寶貴的數(shù)據(jù)。第谷本人是地心說的支持者，他認為太陽和其他行星一起繞地球運動，地球是宇宙的中心，是不動的。

開普勒（1571-1630），德國人，天文學家。最初，他是哥白尼日心說的擁護者。與別人不同的是，開普勒不是盲目的接受一個觀點，他通過自己的計算，發(fā)現(xiàn)哥白尼的體系與實際觀察到的數(shù)據(jù)有出入，他對天體運行的規(guī)律有自己的思考。1600年，開普勒獲得了成為第谷助手的機會，在第谷逝世后，獲得了第谷所有的觀測數(shù)據(jù)。之后開始進入長期的計算中，他發(fā)現(xiàn)，如果天體是按照正圓均速運動，所預測的天體運動與第谷觀測的結(jié)果有較大的出入。他堅信第谷的數(shù)據(jù)是準確的，那么問題就出在天體運動規(guī)律的假設了。在之后的研究中，他發(fā)現(xiàn)活性經(jīng)常偏離圓軌道，經(jīng)過70多次的反復修正，否定了圓軌道，最后確定了橢圓。直到1609年，他在《新天文學》中公開發(fā)表了兩條行星運動的規(guī)律。九年后，他又發(fā)現(xiàn)了第三定律。他用簡單的三句話，概括了太陽與行星的運動規(guī)律，被后人稱為“天空立法者”。這三句話就是我們現(xiàn)在所說的開普勒三大定律：軌道定律、面積定律和周期定律。軌道定律闡述了行星圍繞太陽運動的軌道是一個橢圓，太陽在橢圓的焦點上。面積定律解釋了天體運動時快時慢，“太陽與行星的連線在相同的時間內(nèi)，掃過的面積是相等的”，所以近日點的行星運動的速度比遠日點的速度要快。周期定律：，其中T表示的是天體繞太陽運動的周期，a表示的是天體繞太陽運動的橢圓軌道的半長軸。

3引力來源的思考及牛頓萬有引力定律的建立

伽利略（1564-1642），意大利人。他是哥白尼的日心說的擁護者，認為地球是運動的。他始終堅信圓運動是最簡單最和諧的運動，而不關注開普勒的橢圓軌道。他應用望遠鏡來觀測天體，得到很多肉眼無法觀測的現(xiàn)象，比如他發(fā)現(xiàn)了金星的盈虧變化，更加否定了地心說，給予日心說有力的支持。伽利略認為，天體做圓周運動，是遵從慣性原理的，它們的這種圓周運動不需要力來支持，是自然維持的。在力學方面，他推崇實驗和數(shù)學推理相結(jié)合的科學方法。否定了亞里士多德重的物體比輕的物體下落的快的觀點。他又對自由落體運動進行了研究，提出了自由落體運動是勻變速運動。他不僅對地面上的落體運動建立了正確的認識，更為近代科學創(chuàng)立了新的研究方法，標志著近代物理學的開端。

笛卡爾，與伽利略的觀點一樣，行星的軌道是正圓，是勻速運動的。他提出若沒有外因的作用，運動的物體將以相同的速度沿同一直線運動，他強調(diào)慣性運動的直線性。但他否認天體運動是由于引力的作用而產(chǎn)生的。他認為太陽周圍有“漩渦”，由于“漩渦”的作用，行星才得以不停做圓周運動。地球周圍也存在“漩渦”，這才使得物體能落地。

荷蘭科學家惠更斯做了一個實驗，發(fā)現(xiàn)碗內(nèi)漩渦的水讓小石子拉到漩渦的中心，從而更加支持笛卡爾的漩渦模型。但令人驚奇的是，惠更斯在研究單擺問題的時候，已經(jīng)發(fā)現(xiàn)圓周運動的物體需要向心力，并推算出向心力定律，但卻未將它用在天體問題上，未發(fā)現(xiàn)天體運動的力是來自于引力。

伽利略、笛卡爾認為物體在不受其他外力作用時，將會沿著直線運動，他們的觀點引發(fā)新的問題：（1）既然不受外力的時候物體做直線運動，那么天體的圓周或橢圓運動，需要力來維持，現(xiàn)在需要解決的問題就是找出這個力的規(guī)律。（2）證明引力隨距離變化的關系。

牛頓（1642-1727），1687年出版的《原理》中提出了萬有引力定律，一方面解釋了落體運動及行星運動的規(guī)律，另一方面，他通過“月地檢驗”，將地上的落體運動和天上的行星運動統(tǒng)一起來，得到了簡潔的運動規(guī)律。開普勒總結(jié)出了行星運動的規(guī)律，但并未能做出為什么運動的解釋，牛頓恰在這方面做了研究。在惠更斯提出離心力（向心力）公式后，很多科學家都從開普勒的周期定律推出了引力與距離的平方成反比的關系。之后，科學家們又思考能否從中推導出物體的軌跡形狀。胡克聲稱自己已經(jīng)可以證明所有天體的運動規(guī)律，但他并未公布自己的結(jié)果。后來，1684年8月，哈雷拜訪了牛頓，希望他可以幫助解決這個問題。牛頓聲明自己早已做過證明，但是找不到手稿，他就重新證明了一次，那個時候牛頓已經(jīng)發(fā)明了微積分，為他求解橢圓軌道的問題提供了數(shù)學基礎。寫了論文《論軌道上物體的運動》寄給哈雷，這篇文章成為后來出版的《論自然科學之數(shù)學原理》的第一部分內(nèi)容。

牛頓繼續(xù)深入思考，9個月后完成《論物體的運動》，解決了慣性問題，明確了引力的普遍性。牛頓思考地上蘋果落地的重力和天上月亮繞地運動的力是否為同一種力，這就是后人所說的“月地檢驗”。牛頓提出，在地面上拋射出一塊石子，石子將會在空中做曲線運動，然后落在地面上；如果增大初速度，石子落地時離出發(fā)點就越遠。設想速度增加到非常大，石子將會經(jīng)過好多里的路徑才會落到地上；再繼續(xù)增大速度，它將會從地球邊上掠過。這就成為了我們現(xiàn)在所說的近地衛(wèi)星。如果在月球的軌道上，給予合適的速度拋物體，那么物體將會繞地運動。這個物體可以是石子，也可以是蘋果，或是月亮。如果月亮所受地球的引力和地面上的物體所受的引力遵從同樣的規(guī)律，那么就實驗了“天”“地”的統(tǒng)一。牛頓通過當時已有的月球繞地運動的周期，月地距離，算出月亮繞地運動的（向心）加速度是地面物體自由落體加速度的，兩者距地球中心的距離之比為60，說明地球?qū)υ铝恋囊偷孛嫖矬w所受的引力都和距離遵從平方反比的關系，實現(xiàn)了“天地合一”。牛頓在研究天體問題的過程中，也解決了物理運動的本質(zhì)問題，建立了以三大運動定律為基礎的力學體系。在1687年出版的《自然哲學之數(shù)學原理》中，牛頓進行了完整的闡述。

亨利·卡文迪許（1731-1810），英國人，著名的物理學家、化學家。卡文迪許的扭秤實驗，被評為“十大最美物理實驗”。牛頓運用自己的強大的數(shù)學能力和大膽的推論，指出萬物之間都存在引力。但是地球上兩個物體之間的引力實在太小了，人們沒辦法測量，卡文迪許和米歇爾（1724-1793）設計的扭秤實驗，彌補了這個遺憾。在米歇爾逝世后，卡文迪許繼續(xù)鉆研，在1798年，卡文迪許通過實驗，測出了地球的密度（發(fā)表文章《地球密度的實驗確定》）。當時他并未去計算引力常量G，但后人根據(jù)他的實驗數(shù)據(jù)，得出，并計算出具體數(shù)值，歷史上仍稱他為“第一個稱起地球質(zhì)量的人”。