基于模糊邏輯理論的前饋控制器設計方法研究

張彥龍，張 馳，趙 飛，杜文華，柳 瑞,馬 駿

(1.中國科學院 寧波材料技術與工程研究所， 寧波 315201；2.中北大學， 太原 030051)

?

基于模糊邏輯理論的前饋控制器設計方法研究

張彥龍1,2，張 馳1，趙 飛1，杜文華2，柳 瑞1,馬 駿2

(1.中國科學院 寧波材料技術與工程研究所， 寧波 315201；2.中北大學， 太原 030051)

永磁直線電機在變速運行時會產生較大的位置跟蹤誤差，嚴重影響直線電機的動態(tài)跟蹤精度。運用模糊邏輯理論設計前饋控制器是實現降低系統(tǒng)位置跟蹤誤差的重要手段之一。首先在MATLAB/Simulink中搭建位置閉環(huán)、速度閉環(huán)和電流閉環(huán)三環(huán)控制器。為降低電機在運行時的振動，將S曲線作為指令信號加入到系統(tǒng)中，根據前期電機調試經驗并結合模糊邏輯理論設計前饋控制器，實現降低直線電機運行時的位置跟蹤誤差。仿真和實驗結果表明，模糊邏輯前饋控制器的加入有效地降低了系統(tǒng)運行時的位置跟蹤誤差。

永磁同步直線電機；前饋補償；模糊邏輯前饋控制器；S型曲線

0 引 言

永磁同步直線電機在高速高精度定位系統(tǒng)中的應用日益增多。永磁同步直線電機使得系統(tǒng)的傳動鏈得到簡化，減少了因傳動鏈而引入的誤差，避免了滾珠絲杠傳動中的反向間隙、慣性、摩擦力和剛度不足等缺點，提高了定位系統(tǒng)運行時的速度及加速度，拓寬了控制帶寬范圍，積極推動了高速高精密加工的發(fā)展。

直驅進給系統(tǒng)若只采用負反饋控制，可以在一定程度上減小誤差，但由于系統(tǒng)的控制帶寬和增益會受其機械結構本身的限制，大大增加了其應用到高速高精度場合的難度。因此，將前饋控制引入到負反饋系統(tǒng)中以提高系統(tǒng)的控制精度是非常必要的。零相位誤差跟蹤控制 (ZPETC)[1-3]可以消除反饋環(huán)的所有極點以及可以消除的零點，并且可以消除不可消除的零點所引起的相位誤差，使得期望輸出到實際輸出的頻率響應相位變化為零，極大地減小了系統(tǒng)的跟蹤誤差。當反饋控制器和控制對象模型階數較高時，設計出的零相位誤差跟蹤控制器就會有非常高的階數。此時，該控制器很難應用于實時控制系統(tǒng)中。當干擾信號影響控制系統(tǒng)時，零相位誤差跟蹤控制器會放大命令信號中的高頻成分或放大部分噪聲，產生高頻擾動。重復學習[4-6]主要應用于因非線性對象模型和參數不確定性所引起的跟蹤控制問題，通過不斷地學習，改善系統(tǒng)控制的性能。由于重復學習需要特定系統(tǒng)和同樣的初始條件，而控制系統(tǒng)具有多樣性，使得學習控制算法收斂性具有很大的局限性。因此，重復學習主要應用在不基于模型的低速控制系統(tǒng)中，在要求強實時性的控制系統(tǒng)中應用難度較大。張剛和潘霞遠等人[7-8]提出了將指令速度信號和加速度信號分別乘上一個合適的系數作為前饋量加入到控制系統(tǒng)中，雖然提高了軌跡跟蹤精度，但在變速區(qū)電機的軌跡跟蹤精度仍然很大。線性與指數加減速算法在變速階段會出現加速度突變現象，該現象會使生成的速度曲線不夠平滑。不平滑的指令加速度信號容易在軌跡生成中產生高頻擾動分量，該分量會引起直驅進給系統(tǒng)不必要的振動。為得到平滑的速度和位置軌跡指令曲線，降低電機運行時的振動，本文采用S型曲線作為位置指令信號[9]。模糊控制器在設計中不需要受控對象精確的數學模型，使得控制策略易于理解，設計簡單并便于應用。模糊控制系統(tǒng)具有較強的魯棒性，外界干擾對其控制的影響被大大削弱了，尤其適用于非線性、時變和具有滯后系統(tǒng)的控制。本文結合模糊邏輯理論，設計出了模糊前饋控制器，有效提高了電機運行時的位置跟蹤精度，尤其是電機在指令信號作用時的位置跟蹤精度。

1 傳統(tǒng)復合前饋控制器的設計

本文首先以永磁同步直線電機為被控對象，建立位置閉環(huán)、速度閉環(huán)和電流閉環(huán)三環(huán)控制器。其中，電流環(huán)采用id=0矢量控制方式。此時，電機的輸出電流和電機產生的推力成正比。永磁同步直線電機的動力學方程可表示：

(1)

(2)

式中：F為電磁推力；m為電機動子質量；a為電機的加速度；kv為電機的粘滯系數；v為電機的運行速度；K為電機推力常數；iq為電機的q軸電流。

由式(1)和式(2)可知，永磁同步直線電機速度的產生，粘滯阻力的克服以及其他干擾因素的抑制主要由q軸電流來提供。負反饋是根據系統(tǒng)的指令與實際的誤差值進行控制的，輸出量發(fā)生變化形成誤差值進而負反饋系統(tǒng)產生控制作用。故反饋控制會導致系統(tǒng)響應滯后。當對系統(tǒng)的速度和精度要求不高時常采用此類控制，但對電機的響應速度和精度要求較高時，單純的反饋控制便不能滿足要求。將指令速度信號和加速度信號分別乘上一個合適的系數作為前饋量加入到控制系統(tǒng)中，可以有效提高系統(tǒng)的響應速度，彌補負反饋犧牲系統(tǒng)響應速度來抑制擾動的缺點。常用伺服控制前饋算法框圖如圖1(a)所示。根據前期工作的經驗總結，復合前饋增益的初值按以下原則選取:

(3)

(4)

式中：kv為滑動粘滯系數；k為電磁力常數；m為動子的質量。

(a) 常用前饋控制圖

(b) 模糊前饋控制圖

圖1 伺服控制系統(tǒng)框圖

2 模糊邏輯前饋控制器的設計方法

模糊控制器的系統(tǒng)框圖如圖2所示。由圖2易知，本文設計的模糊控制器具有指令速度v0和指令加速度a0兩個輸入變量；V0和A0為對應的模糊量；U為輸出模糊量；u為控制器作用到系統(tǒng)中的輸出精確量。

圖2 模糊控制過程

對于指令速度，本文采用NB，NM，NS，ZO，PS，PM和PB等7個語言變量來描述，指令加速度由N，Z和P等3個語言變量來描述。隸屬函數采用三角形隸屬函數來表示，曲線形狀如圖4所示。

本文模糊控制規(guī)則的句型運用“ifV0andA0thenU”的形式。每條模糊語句均對應了一個模糊關系Fi。各模糊語句之間存在“或”關系，故模糊控制規(guī)則總的模糊關系：

(5)

若將模糊量V0及A0帶入模糊規(guī)則，則求得U的表達式：

(6)

式中：“∨”表示取兩數最大，“×”表示直積， “°”為關系合成運算。模糊關系定義為，設U，V為論域，若R∈F(U°V)，稱R為U到V的模糊關系。

本文的模糊控制器采用Mamdani推理合成算法，其最大的特點是將模糊蘊含關系A→B表示為直積的形式，即:

(7)

本文基于Mamdani法并結合前期的調試經驗制定的模糊控制規(guī)則如表1所示。每條模糊語句均代表針對某一確定情況的應對方法。

表1 模糊控制規(guī)則表

通過仿真和實驗分析發(fā)現，隸屬函數的形狀和分布規(guī)律會對控制輸出產生影響，尤其是鄰近的隸屬函數間的重疊度會對控制器的性能產生較大影響。重疊指標的定義如式(8)所示，圖示如圖3所示。若鄰近的隸屬函數不重疊會導致控制性能下降，甚至會出現控制死區(qū)。重疊率越大、重疊魯棒性越強，模糊控制器抵抗特性參數變化的能力越強，控制靈敏度越低，反之亦然。因此，對于比較復雜的被控對象，選用一組固定重疊率值的三角隸屬函數時控制效果并非最佳。本文采用的模糊邏輯方法根據不同階段的控制結果，通過調整隸屬函數的斜率，即整定重疊率，使控制器控制效果更好，可調斜率隸屬函數曲線如圖4所示。由于本實驗需要對斜率參數在線實時調整，而模糊工具箱中的參數不能在dSPACE的Controldesk界面中在線實時調整，故本文的模糊控制器在MATLAB中編寫并加載到dSPACE中。

c=(重疊范圍)/(兩相鄰隸屬函數覆蓋范圍) (8)

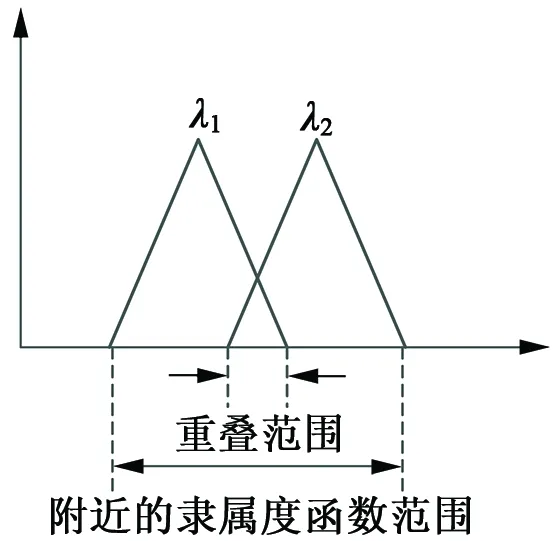
圖3 重疊率計算圖

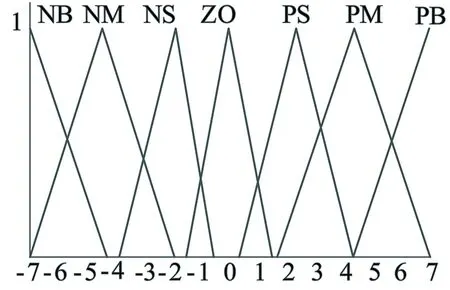
圖4 可調斜率的三角形隸屬函數曲線

3 基于模糊邏輯前饋控制器的仿真實驗及結果討論

3.1 S型軌跡曲線的設計

S型曲線指的是直驅進給系統(tǒng)在變速階段時的速度曲線為S型。S曲線在變速時的加加速度的值為常數，適當的調整加加速度值可以有效的減小給機械系統(tǒng)造成的沖擊。同時，針對不同的被控對象，設定加速度和加加速度兩個值可實現柔性加減速控制。本文電機的運行位移為0.05 m，最大速度為0.3 m/s，最大加速度為3.82 m/s2，加加速度為48 m/s3。

3.2 仿真實驗及結果分析

本文在MATLAB/Simulink環(huán)境中建立位置閉環(huán)、速度閉環(huán)和電流閉環(huán)控制系統(tǒng)，仿真對象為永磁同步直線電機，其參數如表2 所示。根據上述的原理可以設計出模糊邏輯前饋控制器，其理論框圖如圖1(b)所示。電機的運行軌跡如圖5所示，其控制結果如圖6所示。由圖6可以看出，當系統(tǒng)無前饋控制時，系統(tǒng)的位置跟蹤誤差較大；當系統(tǒng)加入傳統(tǒng)前饋時的位置跟蹤誤差的最大值為16.64 μm；當系統(tǒng)加入固定斜率模糊邏輯前饋控制器時的最大位置跟蹤誤差為2.15 μm；當系統(tǒng)加入可調斜率模糊邏輯前饋控制器時的最大位置跟蹤誤差降為1.7 μm。由此可得，由可調斜率模糊邏輯前饋控制器補償后的位置跟蹤誤差較傳統(tǒng)前饋補償后的位置跟蹤誤差降低了90%以上，且當指令信號結束后系統(tǒng)以更短的時間進入到-1～1 μm的區(qū)間內。由該圖還可以看出，可調斜率模糊邏輯前饋控制器補償后的位置跟蹤誤差較傳統(tǒng)前饋補償的最大位置跟蹤誤差降低了近0.5 μm。驗證了本文提出的可調斜率模糊邏輯前饋控制器的可行性。應當指出的是，由于模糊控制規(guī)則為有限數量的原因，使得系統(tǒng)的位置跟蹤誤差不能被完全抑制。

圖5 S曲線加減速過程

(a) 加入前饋補償前后對比

(b) 加入不同前饋補償對比

圖6 補償前后及不同補償方法下的位置跟蹤誤差曲線

4 基于模糊邏輯前饋控制器的補償實驗及結果討論

4.1 實驗配置

論文提出的模糊邏輯前饋控制器方法被應用在一臺XY直線電機，其Y向電機作為被控對象。該方向直線電機相關參數如表2所示。位移由MicroE MII30型號的光柵尺測量，其測量精度為0.4 μm。試驗臺控制器由dSPACE1103控制開發(fā)系統(tǒng)搭建，驅動器采用Copley Xenus型驅動器，電機的冷卻由圖中所示的空氣壓縮機提供。整個永磁同步直驅電機伺服系統(tǒng)平臺如圖7所示。

圖7 實驗配置

4.2 模糊邏輯前饋補償實驗及結果討論

在MATLAB/Simulink中搭建電機的位置閉環(huán)和速度閉環(huán)控制器，并將其加載到dSPACE1103中，結合Copley Xenus驅動器使電機按照預設的軌跡運行。首先在Simulink中編寫模糊邏輯前饋控制器模塊的程序并將其加載到dSPACE1103中以實現實時調整。本實驗的輸入軌跡仍按上節(jié)給出的S型軌跡，其最大的運行速度為300 mm/s。從圖8(a)可以看到，在未加入前饋補償時，直線電機運行時的位置跟蹤誤差比較大，加入前饋補償后的位置跟蹤誤差被明顯抑制。由圖8(b)可知，加入傳統(tǒng)前饋補償時的位置跟蹤誤差為15.45 μm；加入固定斜率模糊前饋補償后的位置跟蹤誤差為8.3 μm；加入可調斜率模糊前饋補償后，其位置跟蹤誤差降為5.3 μm。從實驗結果可以看出，可調斜率模糊前饋補償后的位置跟蹤誤差較傳統(tǒng)前饋補償降低了60%以上。同時，可調斜率模糊邏輯前饋控制器補償后的位置跟蹤誤差較固定斜率模糊前饋補償的位置跟蹤誤差明顯降低。應當指出的是，仿真所用的被控對象的數學模型和電機的實際模型有一定差異，導致仿真結果和實驗結果略有不同；電機在運行時所受噪聲及振動的影響，使得補償后的位置跟蹤誤差波動較大。同時，電磁推力常數隨著位置變化也會略有不同，導致電磁推力和q軸電流并非呈嚴格的正比關系，電磁推力的非線性也會引起電機的位置跟蹤誤差的波動。論文的下一步工作將電磁推力常數變化的影響也加入到補償系統(tǒng)中，并降低電機運行時的噪聲影響，使得補償效果更好。

(a) 加入前饋補償前后對比

(b) 加入不同前饋補償對比

圖8 補償前后及不同補償方法下的位置跟蹤誤差曲線

5 結 語

針對電機在變速運行時存在較大的位置跟蹤誤差，本文建立了基于模糊邏輯理論的前饋補償策略。首先搭建位置閉環(huán)、速度閉環(huán)和電流閉環(huán)三環(huán)控制器。然后為減小電機運行時的振動，使電機按照S型軌跡運動，最后根據電機運行時的位置跟蹤誤差設計模糊邏輯前饋控制器。通過一臺XY永磁同步直驅電機的實驗研究表明，該方法明顯抑制了指令信號作用時的位置跟蹤誤差，一定程度上減小了指令信號結束后的位置誤差降到-1～1 μm的時間。同時該方法實現過程較為簡單，不需要額外的實驗設備和傳感器，實時性強。

[1] 陳興林,劉川,周乃新,等.基于ZPETC-FF和DOB的精密運動平臺控制[J].哈爾濱工業(yè)大學學報,2014，46(1)：1-6.

[2] 李志軍,劉成穎,孟凡偉,等.基于ZPETC和DOB的直線電機控制器設計及實驗研究[J].中國電機工程學報,2012,32(24):134-140.

[3] KAMIGAKI Y,OHISHI K,NABATA Y,et al.Zero phase error tracking control system with multi harmonics disturbance suppression loop[C]//11th International Workshop on Advanced Motion Control,AMC.2010:377-382.

[4] ROTARIU I,STEINBUCH M,ELLENBROEK R.Adaptive iterative learning control for high precision motion systems[J].IEEE Transactions on Control Systems Technology,2008,16(5):1075-1082.

[5] HELFRICH B E,LEE C,DOUGLAS A B,et al.Combined H∞-feedback control and iterative learning control design with application to nanopositioning systems[J].IEEE Transactions on Control Systems Technology,2010,18(2):336-351.[6] 蔡滿軍,趙成圓.永磁直線同步電機的自適應迭代學習控制[J].微特電機，2013，42(6):48-54.

[7] 張剛,劉品寬,張波,等. 直線電機精密運動平臺軌跡跟蹤控制器設計[J].光學精密工程,2013,21(2):371-379.

[8] 潘霞遠. 高精度永磁直線伺服系統(tǒng)的研究[D].廣州：廣東工業(yè)大學,2008.

[9] 張碧陶,高偉強,沈列,等.S曲線加減速控制新算法的研究[J].機床與液壓,2009,37(10):27-29.

[10] 林輝,呂帥帥,樊明迪.基于模糊前饋的永磁同步電動機滑模矢量控制系統(tǒng)[J].微特電機,2013,41(4):35-37.

[11] 朱爾立,舒志兵,沈陽,等.基于模糊控制的激光加工間隙控制設計分析[J].機械設計與制造,2015(8):13-15.

[12] CAZAREZ-CASTRO N R,MALDONADO Y.Design and hardware implementation of a closed-loop stable fuzzy controller[C]//2014 11th International Conference on Electrical Engineering,Computing Science and Automatic Control (CCE),IEEE,2014:1-6.

[13] AKBAR M A.Simulation of fuzzy logic control for DC servo motor using Arduino based on MATLAB/Simulink[C]//2014 IEEE International Conference on Intelligent Autonomous Agents, Networks and Systems (INAGENTSYS),IEEE,2014:42-46.

Research of the Design of Feedforward Controller Based on Fuzzy Theory

ZHANGYan-long1,2，ZHANGChi1，ZHAOFei1，DUWen-hua2,LIURui1,MAJun2

(1.Ningbo Institute of Industrial Technology,CAS,Ningbo 315201,China；2.North University,Taiyuan 030051,China)

Position tracking error will occur when permanent magnet linear motor is moving, especially working with variable speed.The error influences the dynamic tracking accuracy of linear motor seriously. Feedforward controller designed by using fuzzy logic theory is one of the important means to reduce system position tracking error. First, position closed-loop, speed closed-loop and current closed-loop controller were built in the MATLAB/Simulink. In order to reduce the vibration of the motor when it was running, the S curve was treated as the command signal. According to the experience of adjusting the motor earlier and the fuzzy logic theory, feedforward controller was designed to lower position tracking error of the linear motor when it was working. Simulation and experimental results show that the feedforward fuzzy logic controller effectively reduces the system position tracking error at runtime.

permanent magnet synchronous linear motor; feedforward compensation; feedforward fuzzy logic controller; S curve

2015-09-17

國家自然科學基金項目(51207158)；國家自然科學基金項目(51405479)；中國博士后科學基金項目(2015T80639)；寧波市創(chuàng)新團隊(2012B82005)；寧波市重大專項(奧馬特)(2013B-10042,2013B10043)；中科院百人計劃(2015A610146,2015A-610154)；寧波市自然科學基金項目(2014A610084)

TM351;TM359.4

A

1004-7018(2016)06-0001-04

張彥龍(1990-)，男，碩士研究生，研究方向為電機控制。