基于Pro/E的斜齒齒輪副變位系數與側隙的優化設計
羅光漢
(武漢城市職業學院 機械工程與電氣自動化學院,武漢 430064)
基于Pro/E的斜齒齒輪副變位系數與側隙的優化設計
羅光漢
(武漢城市職業學院 機械工程與電氣自動化學院,武漢 430064)
運用Pro/E軟件的行為建模技術,在漸開線斜齒圓柱變位齒輪參數化精確建模的基礎上,創建嚙合齒輪的目標函數與約束條件的分析特征,實現齒輪的變位系數與側隙的優化設計,其計算結果驗證了文章的有效性和實用性。
Pro/E;齒輪副;行為建模;變位系數;側隙;優化設計
0 引言
結合變位齒輪無側隙嚙合方程,采用Pro/E軟件中的SOLVE和FOR語句對漸開線函數中的嚙合角進行求解,實現漸開線斜齒圓柱嚙合齒輪的幾何尺寸精確計算與參數化三維建模[1,2]。通過建立齒輪副質量指標如最大滑動系數ηmax之差的絕對值的目標函數等的分析特征作為優化目標,以變位齒輪的約束條件的分析特征作為設計約束,運用Pro/E軟件的行為建模技術進行優化設計,實現嚙合齒輪的變位系數的優化設計。AGMA 913-A98標準給出了在齒輪副的實際中心距與輪齒法向齒厚設計值條件下的變位系數計算公式與實例[3],對此,在上述的優化操作中,再添加齒輪副的實際中心距與側隙約束條件的分析特征,既獲得變位系數的最優解,也計算出齒輪副的側隙為0.024Mn。
1 齒輪副的目標函數
提高嚙合齒輪抗膠合能力和耐磨損能力,應使主動齒輪的齒頂與從動齒輪除根處的最大滑動系數η1max以及從動齒輪的齒頂與主動齒輪的齒根處的最大滑動系數趨于相等或相近,其目標函數為:

2 變位齒輪的約束條件
2.1保證齒輪加工時無根切
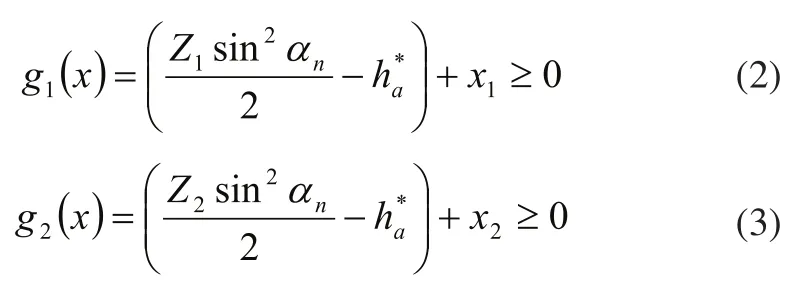
2.2保證有必要的重合度
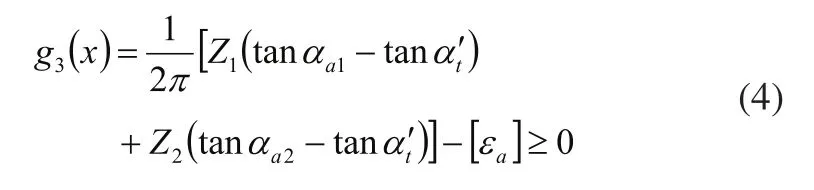
2.3保證有一定的齒頂厚
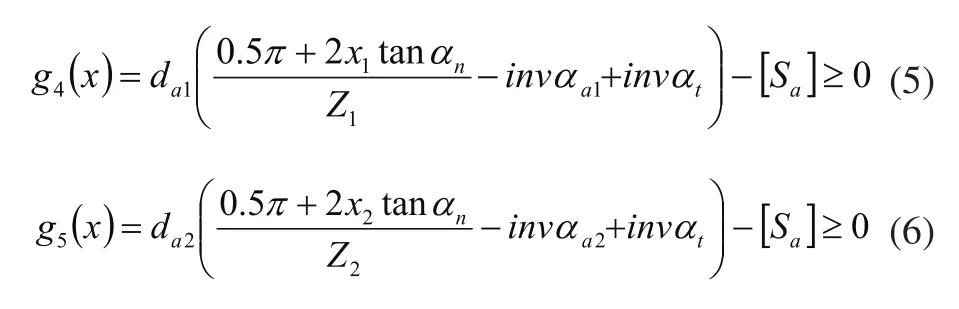
2.4保證齒輪嚙合時不干涉

式(2)~式(8)中,x1、x2為變位系數;Z1、Z2為齒數;為標準壓力角;h*a為齒頂高系數;為齒頂圓的壓力角;為齒輪的端面嚙合角;為許用的端面重合度,一般取為齒輪齒頂圓直徑;[Sa]為許用的輪齒齒頂厚,一般取[Sa]≥(0.25~0.40) Mn;αt為齒輪端面壓力角。
3 運用Pro/E進行齒輪副變位系數的優化設計
3.1定義齒輪副的側隙系數
選擇菜單“工具”→“參數”命令,在打開“參數”對話框中,添加齒輪副的側隙為模數Mn的系數xj與分度圓法向齒厚的設計值S1、S2。
3.2創建齒輪副的幾何關系
選擇菜單“工具”→“關系”命令,在打開的“關系”對話框中,分別將式(1)~式(8)中的齒輪副的最大滑動系數重合度 εα、齒頂厚Sa、分度圓齒厚Sn和實際中心距a'的關系式輸入在“關系”的文本框中,以簡化分析特征中的相應關系式的鍵入。
3.3創建約束條件的分析特征
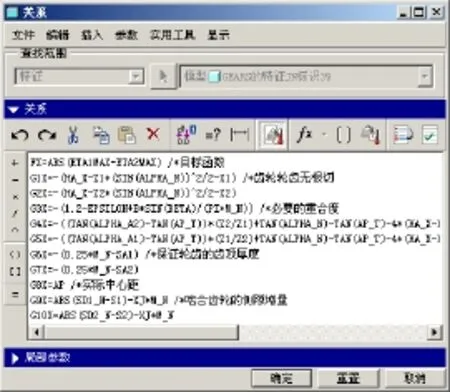
圖1 創建分析特征
3.4設置優化類型及其設計約束與變量
選擇菜單“分析”→“可行性/優化”命令,在打開的“優化/可行性”對話框中,接受“研究類型/名稱”選項組中的“優化”單選項,選擇“目標”下拉列表中的“最小化絕對值”,其分析特征為“FX: JN”。單擊“設計約束”下的“添加”按鈕,系統打開“設計約束”對話框,在其“參數”下拉列表中選取約束條件的分析特征“G1X: JN”與運算符“>=”,在“值”下,選擇“設置”為“0”,單擊“確定”按鈕后,所選約束出現在“設計約束”列表框中的“參數”、“優化”和“值”下;再分別選取“G2X: JN”、“G2X: JN”、…、“G10X: JN”作為設計約束,其中,實際中心距AP的值由具體的設計來確定,分度圓齒厚增量的運算符與值為“=”、“0”。
單擊“設計變量”下的“添加參數”按鈕,在打開的“參數選取”對話框中,分別選取“X1:GEARS”、“X2:GEARS”及“XJ:GEARS”三個參數作為設計變量,其中,變位系數與側隙系數的“最小”、“最大”值分別設定為“-1”、“1”與“0”、“1”。
選擇對話框中的菜單“選項”→“優先選項”命令,選取“優先選項”對話框中的“運行”選項卡,將“收斂性%”的缺省值“0.500000”修改為“0.000001”。完成上述操作后的“優化/可行性”對話框如圖2所示。

圖2 “優化/可行性”對話框

圖3 齒輪副參數的優化值
3.5優化設計
4 計算實例
1)文獻[1]中的單級圓柱齒輪減速器。已知:mn=6mm、Z1=29、Z2=101、a'=400mm、B=160mm,尋求齒輪抗膠合能力和耐磨損能力的變位系數。其優化結果為minf(x)=0.000003、x1=0.371930、x2=0.315654、文獻中采用封閉圖的計算結果為|f(x)|=0.016425、x1=0.38、x2=0.3076、
2)根據文獻[3]中的變位齒輪計算實例(B.3),其優化結果為minf(x)=0.400879、x1=0.534291、x2=0.000015、a'=236.664500、xj=0.024006,如圖3所示,
【】【】與文獻中的計算結果完全一致,其側隙
5 結論
運用Pro/E軟件的行為建模技術,無需編程及建立程序框圖、選擇或構造相應的優化迭代計算算式,可根據實際需要對優化目標、優化類型(優化、可行性與多目標設計研究)、約束條件進行相應的選取與優化計算,如齒輪副的齒根彎曲強度、最大承載能力等,工程實用性強。
本文中的斜齒圓柱變位齒輪三維模型的螺旋角β取值范圍為0°~80°、齒數為Z≥3。考慮到三維模型的再生進程,將模型樹中的齒輪所有造型特征創建為“組LOCAL_GROUP”并予以隱含,在完成齒輪變位系數等變量的迭代計算之后,再將組特征恢復,以適時顯示齒輪的三維模型,為其進一步的設計分析提供可靠的依據。
[1] 張展.齒輪設計與使用數據速查[M].北京:機械工業出版社,2009:127-133.
[2] 羅光漢,編著.Pro/ENGINEER Wildfire 5.0模具產品設計實例教程[M].北京:北京郵電大學出版社,2014:138-149.
[3] American Gear manufacturers Association.AGMA 913-A98 Method for Specifying the Geometry of Spur and Helical Gears[S].Virginia:AGMA,1998.
The optimization of modification coefficient and backlash of helical gear pairs based on Pro/E
LUO Guang-han
TP391.7
B
1009-0134(2016)02-0115-02
2015-10-09
羅光漢(1964 -),男,湖北新洲人,高級工程師,本科,主要從事產品設計與模具CAD/CAM教學與研究工作。

