以“教學生思考"為目標的數學教學案例研究

夏小強

1問題的提出

南京師范大學的涂榮豹先生認為，數學教學的目標有三個：一是使學生愛學；二是會學；三是發展學生的認識力。發展學生的認識力，指的就是數學教學要教學生學會思考。

教師在教學過程中，對數學知識的呈現方式存在差異，這種差異對學生獲得數學知識也許影響不大，但對學生數學思維活動的影響，卻可能有很大的差別。

2教學內容說明

向量是刻畫現實世界的重要數學模型，力、速度、位移等都是向量的實際背景，可以用向量加以刻畫和描述。用什么樣的數學模型來刻畫位移、速度、力這樣的量？這個數學模型有什么性質與應用？這就是《平面向量》的中心問題，也是本章的知識學習的固著點。

向量的數量積是在向量的線性運算基礎上學習的一種新的運算，向量的線性運算是封閉性運算，而向量的數量積運算是非封閉性運算，運算的對象是二元的，而運算的結果又是一元的，這種運算的非封閉性對學生的認知造成了很大的失衡。

3教學案例分析

筆者近期聽了兩堂關于“平面向量的數量積”的課，兩位老師的教學過程都分為五個環節：問題情境——抽象模型——辨析模型（內涵、外延）——模型性質（運算律）——數學應用，兩位老師都是以“問題”的形式來推動教學過程。

本文結合其中的環節一和環節四，來探究在教學中如何實現教學生“學會思考”。

3.1環節一問題情境

甲教師：

師：（問題1）向量的運算有向量的加法、減法、數乘，叫做向量的線性運算，那么向量與向量能否“相乘”呢？

生：能。

師：向量與向量“相乘”這種運算怎么定義呢？

生：應該不是線性運算。

師：為什么？

生：老師，向量的加法、減法、數乘，叫做向量的線性運算，向量與向量“相乘”沒有和它們放在一起學，那肯定和它們不一樣了。

師：怎么個不一樣法？

生：……

師：我們是怎么得到向量的線性運算的，它的結果是什么？

生：是通過將實際生活中，物理中的矢量的合成與分解，速度在某時問段的位移抽象出來的，得到的結果還是向量。

師：你想一想，向量與向量“相乘”的結果是什么呢？

生：應該不是向量了。

師：結果不是向量，只能是什么？

生：數……數量……（不是很肯定）

師（點頭）：是數量，我們在實際生活中有這樣的物理背景嗎？

生：做功，力做功的結果就是標量，是一個數。

師：好，我們來分析這個物理背景。看看從求功的運算中可以抽象出什么樣的向量運算？

乙教師：

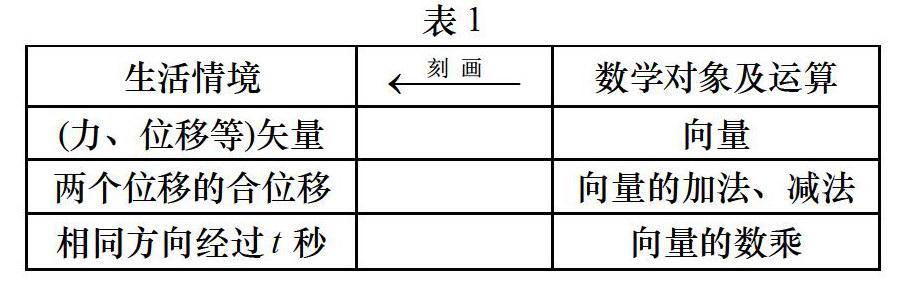
師：前面我們已經學過的向量、向量的加減法、實數與向量的數乘，向量的加法、減法、向量的數乘我們稱之為向量的線性運算。它們都是對實際問題的刻畫。（附表1）

師：（問題1）向量的線性運算可以刻畫出所有的矢量運算嗎？

生：（思考了一會）不能，不能形容矢量的做功運算。

師：為什么？

生：矢量的做功得到的結果是一個標量，也就是數，而你列舉的三種運算得到的結果都是向量。

師：那怎么辦？

生：應該引入一種新的運算，用這種運算來刻畫力的做功。

師：你準備如何定義這種運算？

生：現在還沒想好，我想我們應該先分析矢量做功這個物理背景，找出這個物理背景中和數學有關的元素。

師：研究數學元素的目的是什么？

生：建立數學的量的關系，就像從力的合成與分解中，得出向量的加法、減法一樣。

師：對，建立物理背景中數學的量的關系就是建立數學模型，下面，請大學先分析做功這個物理背景。

教學意圖

甲教師：從數學知識內部發展的需要引入概念，前面學習了向量的線性運算，接下來就應該學習向量的非線性運算，并根據線性運算的結果，引導學生得出新運算的結果是數，側重數學知識的聯系和對比。

乙教師：從實際問題中抽象出向量的概念及運算（數學模型），然后用數學的方法研究數學模型，最后再運用數學模型去解決實際問題。突出了知識的來龍去脈，有助于學生對數學完整的認識。

案例分析

情境的引入要能體現學習新知識的必要性，學習新知識的必要性一般有兩種情況：一是從數學概念體系的發展過程中引入新概念，也就是從數學的內部出發，在原有知識的基礎上，通過歸納、比較、分析等思維活動，尋找新知識與原有知識的區別與聯系，建立新的知識，甲教師正是采用這一方式引入的；二是從解決實際問題的需要出發引入新概念，原有的知識不能解決新的問題，需要引入新的知識來刻畫，乙教師是采用這種方式引入的。

甲教師的引入雖然體現了新知識與原有知識的聯系，但是學生不能認識到學習向量的數量積的必要性，只是因為前面學過了向量的線性運算，所以今天就要學非線性運算，但是學習這個知識有什么用？非線性運算是怎么來的？這些都是通過老師以設問的方式提出來的，雖然學生也能在老師的引導下去研究，但這是一種停留在數學知識本身的學習，這種學習相對被動，學生被老師牽著走，學生的思維難以得到激發。

乙教師的問題情境能夠讓學生認識到學習向量數量積的必要性，教師的提問不是直接指向數學知識本身，而是通過一系列的元認知提示語，引導學生像數學家一樣思考問題，再現知識的“創造”過程，這個“創造”的過程就是研究數學的一般方法。不僅僅向量可以這樣研究，許多別的知識也可以這樣研究，如函數、指數函數、三角函數、數列等。這種教學不僅教了知識，也教會了學生如何思考。

3.2環節四 向量數量積的運算律

甲教師：

師：我們學習了向量的數量積，下面我們來學習向量的數量積的運算律。

（問題3）實數的運算滿足哪些運算律呢？

生：交換律、結合律、分配律。

師：請同學們類比一下，向量的數量積滿足交換律、結合律、分配律嗎？

（學生計算、思考）3分鐘后，

生：滿足交換律，不滿足結合律。

師：滿足分配律嗎？

生：應該滿足吧。

師：為什么滿足分配律，說說理由，你能證明嗎？

生：……

師：好，大家類比一下實數的運算，應該是滿足分配律的。現在大家還不會證明，是因為我們沒有學向量的投影，現在我們來學習向量的投影。

（教師開始介紹向量的投影）

乙教師：

師：我們剛剛學習了一種新的運算——向量的數量積，學習了一種運算后，下一步我們應該研究什么？

生：研究它的性質。

師：哪些性質？

生：是否滿足運算的交換律、結合律、分配律？

師：滿足嗎？

（學生計算、思考）

生：滿足交換律，不滿足結合律，分配律還不確定。

師：怎么不能確定？

生：不知道怎么證明。

師：那怎么辦？不會證明，就沒辦法知道是否滿足分配律嗎？

生：能不能先用特殊的向量試試看？

師：對啊，你為什么不先試試看呢？

（學生用特殊向量計算、驗證）

生：滿足。

師：為什么滿足？

生：我用好幾個特殊的向量驗證后都滿足了。

師：那不特殊的向量也滿足嗎？你的結論具有一般性嗎？

生：那得證明后才能知道。

師：好，我們下面就來證明這個結論。

教學意圖

甲教師：教師通過設問，引導學生通過類比實數的運算律，證明向量的數量積所滿足的運算律。

乙教師：引導學生回顧學習數學對象的過程，學習數學對象之后，應該學習數學對象的性質，對于在現階段還不能證明的結論，以追問的形式引導學生用猜想、歸納、驗證，最后進行演繹證明。

案例分析

數的運算、向量的線性運算、向量的數量積、矩陣的運算是一個發展趨勢鏈，教學應該從發展的角度理解向量的數量積，引導學生認識到數、向量的運算聯系，也為今后引入矩陣及其運算做了鋪墊。

兩位教師都能通過類比實數，學習向量數量積的運算律。甲教師是直接讓學生去比較，乙教師則是引導學生經歷“新的數學對象——對象的性質——（若可以進行運算）——運算法則”這一過程，這也是概念系統的建立過程，在這個過程中，學生能體會到研究數學的通法，這種教學就能促進學生主動地思考如何去研究數學對象。

當學生遇到困難，不會證明向量數量積的分配律時，甲教師是直接進行下一階段的學習，通過補充新的知識來加以證明。乙教師則是引導學生從特殊到一般，先猜想、再驗證、最后證明，這個過程也是數學新知識的發現過程，數學中的許多定理、結論都是這樣發現的，如費馬定理、龐加萊猜想、希爾伯特問題等，數學家們通過直覺思維猜想某個定理，再通過一些特殊的例子加以驗證，最后以嚴密的方法進行邏輯證明。

當然，學生的發現與數學家的發現是不同的，學生是在教師引導下對知識的“再發現”，這種“再發現”可以幫助學生學會思考，思考解決問題的策略，乙教師的教學能引導學生經歷這種“再發現”的過程。

4結束語

數學是思維的科學，數學的發展蘊含著豐富的思想方法，學生學習數學，不僅僅要學數學知識本身，還要學會像數學家一樣思考。

數學教學是帶領學生對數學知識進行“再創造”的過程，在這個過程中，學生感受數學知識的發生、發展，參與數學結論的發現，參與數學概念系統的創建，從而形成對數學完整的認識，發展理性思維。

教師不僅肩負著教學生知識的任務，更肩負著育人的使命。因此，在教學中如何呈現具體的數學知識，將科學的數學轉換成具有教育任務的數學，使之能發揮培養學生思維的作用，是我們共同追求的理想。