關于擋土墻抗傾覆穩定性的計算
姚存鍇,吳 釗
(西安市水利規劃勘測設計院,西安 710054)
?
關于擋土墻抗傾覆穩定性的計算
姚存鍇,吳 釗
(西安市水利規劃勘測設計院,西安 710054)
經研究認為,有些文獻介紹的巖基上擋土墻抗傾覆穩定安全系數計算新公式存在一定問題。建議仍用傳統的公式計算,傳統公式合理、意義明確、其結果唯一。對土基上擋土墻,當基底應力的最大值與最小值之比值滿足規范要求時,擋土墻抗傾覆穩定安全系數滿足規范要求,即擋土墻抗傾覆穩定,擋土墻抗傾覆穩定性無需驗算。
擋土墻;抗傾覆穩定性;計算
0 前 言
文獻[1]等對擋土墻抗傾覆穩定性的計算作了有益的探討,并推薦巖基上擋土墻抗傾覆穩定安全系數計算新公式為K0=0.5B/e0(式中符號意義見后),公路和鐵路橋涵地基與基礎設計規范(JTGD63-2007和TB1002.5-2005)亦規定上式為橋涵墩臺基礎抗傾覆穩定計算公式,但上式存在一定問題。新公式主要問題是:
(1) 新公式是擋土墻臨界狀態與實際狀態進行比較,僅偏心矩不同,實際上臨界狀態與實際狀態擋土墻是2個形狀尺寸、不同荷載、不同的擋土墻,即偏心矩不同,擋土墻不同。而傳統的抗傾覆穩定計算方法及公式是對同一擋土墻求抗傾覆力矩及傾覆力矩,然后將二者之比作為抗傾覆穩定安全系數K0。
(2) 兩大小相等、方向相同的平面平行力,對任意一點力矩之比值是個變數,矩心愈遠,比值愈小,當矩心無窮遠時,其比值趨近于1。選矩心不同,K0不同,K0為任意值。文獻[1]選矩心為墻基底形心,因矩心太近,因而所得K0偏大,不安全,故得出傳統的抗傾覆穩定計算方法所得的K0偏小的錯誤結論。
本文對文獻[1]的新方法、新公式的問題作了分析。本文還對土基上擋土墻抗傾覆穩定性進行討論。
1 擋土墻傳統的抗傾覆穩定性計算方法
1.1 擋土墻傳統的抗傾覆穩定性計算公式
擋土墻傳統的抗傾覆穩定性計算公式[2]:
(1)
式中:K0為擋土墻抗傾覆穩定安全系數;M1、M2依次為諸力對擋土墻前趾點的抗傾覆力矩及傾覆力矩;[K0]為擋土墻抗傾覆穩定安全系數的允許值。
1.2 擋土墻傳統的抗傾覆穩定安全系數的計算
根據文獻[3-8],設擋土墻為剛體,這種假定足夠準確,地基為基巖,故地基亦為剛體。
任一擋土墻如圖1所示,為了簡化并說明問題,設作用在擋土墻上的荷載僅有自重G及主動土壓力E,將E分解為水平分力Ex及豎向分力Ey,諸力對墻趾點O的力臂如圖所示。作用在擋土墻上的荷載為平面力系,平面力系可合成合力(或力偶)。設R為諸力的合力;R的水平及豎向分力分別為H及V;R在墻基底的作用點為A;C點為基底形心;R的偏心矩為e0;墻基底寬度為B。
將諸力向墻趾點O簡化,則根據理論力學:簡化結果可得合力R,合力為原力系之合力,并得力矩M,力矩等于原力系中所有各力對于簡化中心的力矩代數和。
將諸力向簡化中心O簡化,得合力R,R的豎向分力V=G+Ey,水平分力H=Ex,抗傾覆力矩M1=Ga1+Eya2,傾覆力矩M2=Exh,K0=M1/M2。
合力矩M=M1-M2,M=Ga1+Eya2-Exh,又得M=V(B/2-e0)。我們無法從M1-M2=Ga1+Eya2-Exh或M1-M2=V(B/2-e0)中求得M1及M2,即無法求得M1=V(B/2),M2=Ve0,K0=0.5B/e0,因一個方程中有2個未知數,M1、M2有無窮多組解。即已知M,無法求得M1、M2,進而求得K0。
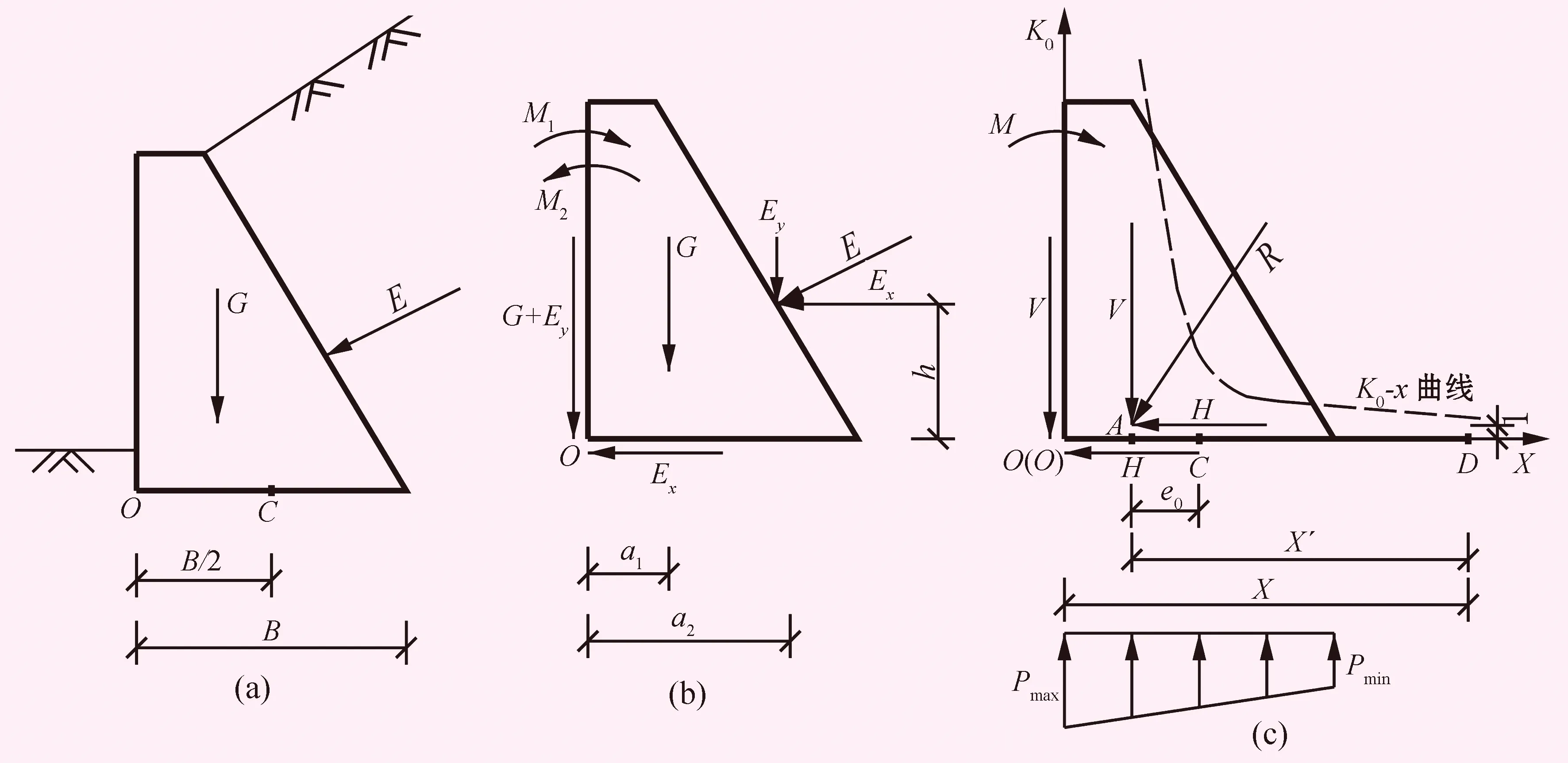
圖1 擋土墻荷載圖
2 巖基上擋土墻抗傾覆穩定計算新方法(即文獻[1]方法)
2.1 文獻[1]巖基上擋土墻抗傾覆穩定計算公式
由于文獻[1]公式推導過程片面有局限性,主要是欠妥。故根據文獻[1]的思想,依據文獻[9-12],重新對文獻[1]公式進行推導,從推導過程和結果可清楚看出文獻[1]的方法及其公式存在的問題。下面先得出普遍適用的通式,其特例即文獻[1]公式。
當R作用于墻趾點O時,M1=M2,M=M1-M2=0,K0=1,擋土墻處于傾覆臨界狀態;當R之作用點A位于O點內側時,M>0,K0>1,擋土墻抗傾覆穩定,A距O愈遠,M愈大,K0愈大,墻愈穩定;反之,當A點位于O點外側時,M<0,K0<1,擋土墻抗傾覆不穩定,且A距O愈遠, |M|愈大,K0愈小,墻愈不穩定。
文獻[1]用抗傾覆穩定臨界狀態與實際狀態相比,將臨界狀態合力R向基底形心C點簡化,根據前述理論力學原理,可得合力R及力矩MK,MK=V(B/2);同時,將實際狀態合力R亦向C點簡化,得合力R及力矩M′,M′=Ve0,文獻[1]擋土墻抗傾覆穩定安全系數的計算公式為:
(2)
對式(2) 討論如下:
(1) 用臨界狀態與實際狀態相比是可以的,問題是怎樣比較。
(2) 第2個問題是簡化中心(即矩心)如何選取,矩心不同,其結果不同。如選簡化中心為O點,如圖1(c)所示,實際狀態R(V,H)作用于A點。臨界狀態R(V,H)作用于O點。實際狀態R對O點取矩,設為M3,M3=V(0.5B-e0),臨界狀態R對O點取矩,設為M4,M4=V·0=0,則根據抗傾覆穩定安全系數的意義,可定義K0=M3/M4,此式與式(1)、(2)的意義不同,0不能作分母,故此式無意義。

文獻[1]的方法及其公式還有其它一系列問題,詳見后。
如圖1(c)所示,在A點內側基底延長線上選一點D,令OD=X,AD=X′,R對D點取矩,令Mk=VX,M′=VX′,則擋土墻抗傾覆穩定計算新公式的普遍形式為:
(3)
設A在C外側時,e0取正值;內側時,e0為負,將X′值代入式(3),則得擋土墻抗傾覆穩定計算新公式的具體形式為:
(4)
如令D點與C點重合,則X=0.5B,X′=e0,代入式(3)或(4),得:
(5)
式(5)即為文獻[1]推薦的擋土墻抗傾覆穩定計算新公式。可見式(5)為式(3)、(4)的特例。
2.2 新公式的討論
(1) 式(4)為普遍適用的通式,它適應范圍廣,可適用一切情況,e0可為正或負,或為0,可很小亦可很大,即A點可在C外側或內側,遠近都行,或在C點。
(2) 當R之作用點A在O點外側時,即e0>0.5B,K0<1;A點與O點重合,即e0=0.5B,K0=1;A點在O點內側,且在O、C之間,即0.5B>e0>0,K0>1;A點與C點重合,即e0=0,K0>1,且比前者大;A點在C點內側,e0<0,K0>1,K0更大。
(3) 式(4)K0為X函數,式(4)單調減。X很小時,K0很大,X→0.5B-e0;K0→∞,X=0.5B-e0時,式(4)無意義;X愈大,K0愈小;當X→∞時,K0→1。式(4)函數圖象見圖1(c)。
(4) 給一個X值,就可得到一個相應K0,X不同,K0不同,K0為任意值。
這是很容易理解的,因兩大小相等、方向相同、且平行的兩平面力R對任一點D(矩心)取矩,得力矩MK及M′,其比值K0大小,只與矩心位置有關,矩心愈遠,K0愈小,K0為不定值,從式(3)及式(4)可清楚看到這一點。
2.3 文獻[1]公式的問題
(1) 文獻[1]公式是式(3)及式(4)的特例。
(2) 適用范圍小,只適用A點在C點外側,即:e0>0;當e0很小時,K0可以很大;當e0→0時,K0→∞;當e0=0時,公式無意義。顯然,這是與實際不符的;當A點在C點內側時,公式不能用。實際工程中A點完全可能在C點內外側,距離C點可能很近也可能較遠,或就在C點。
(3) 依據文獻[1]公式,即認為1.2節中,M1=V(B/2),M2=Ve0,沒有依據。
(4) 由文獻[1]公式得出的K0為任意值,計算所得的K0偏大,因選的X=0.5B小,不安全。所以,得出傳統的擋土墻抗傾覆穩定計算公式計算出的抗傾覆穩定安全系數偏小的結論錯誤。
故文獻[1]公式存在一定問題,作法欠妥。
3 土基上擋土墻抗傾覆穩定計算方法
土基非剛體,而是彈性體。因擋土墻為剛體,故無論是土基還是巖基擋土墻基底應力均按直線分布。
3.1 擋土墻基底應力的計算公式
擋土墻基底應力用式(6)計算:
(6)
式中:Pmax、Pmin依次為基底應力的最大值與最小值;Mc為基底形心C之力矩,Mc=Ve0。
式(6)適用于巖基及土基。
(7)
式中:a、[a]依次為基底應力的最大值與最小值之比值及規范允許值。
由式(7)得:
(8)
將水工擋土墻設計規范[2]中土基[a]列入表1中,并用式(8)計算e0/B,一并列入表1中。從表1中可看到e0/B很小,此時R之作用點A在O、C之間,K0較大。
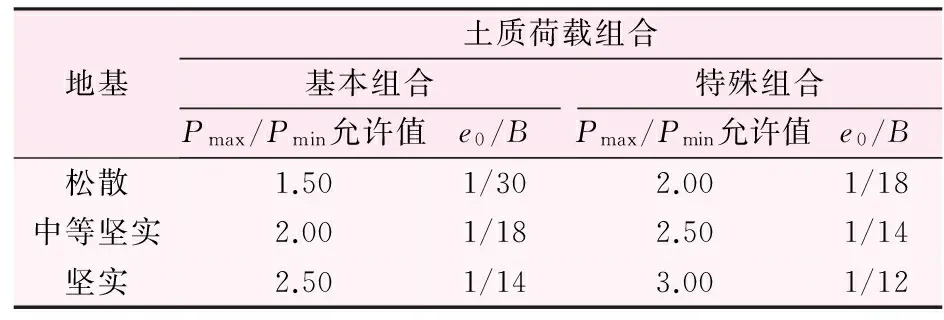
表1 土基上擋土墻Pmax/Pmin允許值與e0的關系表
3.2 土基上擋土墻抗傾覆穩定計算方法
根據規范[2],土質地基和軟質巖石地基上的擋土墻基底應力計算應滿足下列要求:① 在各種計算情況下,擋土墻平均基底應力不大于地基允許承載力,最大基底應力不大于地基允許承載力的1.2倍;② 擋土墻基底應力的最大值與最小值之比不大于規定的允許值。
所以,對于土基上擋土墻只要基底應力之最大值與最小值之比滿足規范允許值,則擋土墻抗傾覆穩定,其抗傾穩定安全數滿足規范要求,擋土墻抗傾覆穩定無需校核,這一點與水工擋土墻設計規范規定相符。
3.3 巖基上擋土墻抗傾覆穩定計算的順序
根據文獻[13-17],將諸力向C點簡化,可得:
(9)
如已知Mc,從式(9)中無法求得M1、M2,M1、M2有無窮多組解。如我們先計算基底應力,即先求Mc,再計算巖基上擋土墻抗傾覆穩定安全系數,因為從式(9)中無法求得M1、M2,故用式(1)無法求得K0。如先計算抗傾穩定安全系數,需先計算M1、M2,用式(1)計算K0,用式(9)計算Mc,再用式(6)計算Pmax、Pmin。故我們應先計算抗傾覆穩定性再計算基底應力,不能反其道而行之,這樣將事半功倍。
4 結 語
(1) 文獻[1]公式存在一定問題,作法欠妥。
(2) 對土基上擋土墻,當基底應力最大值與最小值之比滿足規范允許值時,則擋土墻抗傾覆穩定安全系數滿足規范要求,擋土墻抗傾覆穩定,擋土墻抗傾覆穩定性無需驗算。
(3) 建議用傳統的計算公式(1)計算巖基上擋土墻的抗傾覆穩定安全系數。式(1)意義明確、合理、所得K0唯一。
(4) 巖基上擋土墻抗傾覆穩定及基底應力計算,應先計算抗傾覆穩定安全系數,再計算基底應力,這樣將事半功倍。
[1] 黃岳文. 關于擋土墻抗傾覆穩定分析的討論[J].巖土工程學報,2015(06): 1158-1163.
[2] 中華人民共和國水利部.水工擋土墻設計規:SL397—2007[S].北京:中國水利水電出版社,2007.
[3] 中華人民共和國建設部.建筑地基基礎設計規范:GB50007-2011[S].北京:中國建筑工業出版社,2011.
[4] 中華人民共和國交通運輸部.公路路基設計規范:JTG D30-2004[S].北京:人民交通出版社,2015.
[5] 王渭漳,吳亞中.墻背土壓力分步計算的新理論機工程應用[M].北京:人民交通出版社,1996.
[6] 胡玉銀.擋土墻抗傾覆穩定性分析[J].同濟大學學報,1993, 23(03): 321-323.
[7] 黃勇.擋土墻抗傾覆穩定性分析[J].建筑結構,2002(02):44-45.
[8] 曾革,周志剛.公路擋土墻抗傾覆穩定性設計方法[J].中南大學學報(自然科學版),2009,40(04): 1154-1157.
[9] 張國祥,劉寶琛.墩臺基底的傾覆穩定系數新定義[J].鐵道 學報,2001,23(01): 72-75.
[10] 王成華. 擋土墻傾覆穩定驗算之辨證[J].巖土工程學報,1992,14(04): 72-76.
[11] 余雄飛.地基軟硬程度與擋土墻抗傾覆穩定性[J].巖土工程學報,1998,20(03): 94-46.
[12] 中交第二公路勘察設計研究院有限公司.公路擋土墻設計與施工技術細則[M].北京:人民交通出版社,2008.
[13] 余雄飛,姚 秦.關于擋土墻抗傾覆穩定分析的核心問題[J].華東公路,1996,19(03):57-59.
[14] 方玉樹.擋土墻抗傾覆穩定性計算方法的改進[J].巖土工程學報,2009,12(06): 18-20.
[15] 周相略.關于擋土墻抗傾覆穩定系數計算的討論[J].中南公路工程,1983 (01): 45-53.
[16] 茹建輝.對防洪墻安全系數選擇問題的商榷[J].建筑科學與經濟,2009,19 (01): 31-35.
[17] 鄭建榮,嚴大照,王福根.公路擋土墻穩定問題研究[J].森林工程,1999,15 (02): 41-42.
Calculation of Stability Against Overturning of Retaining Wall
YAO Cunkai, WU Zhao
(Water Resources Planning and Investigation Institute of Xi'an Municipality, Xi'an 710054, China)
The new formula for calculation of the safety factor of the stability against overturning of the retaining wall on rock foundation is doubted. It suggests that the conventional formula shall be still utilized because it is rational, its meaning is definite and the result is sole. Regarding the retaining wall on the earth and when the ratio of the maximum value to the minimum value of the stress on the foundation bottom satisfies the requirement in the code, the safety factor of the stability against overturning of the retaining wall meets the requirement in the code. Namely, the retaining wall against overturning is stable. Its stability against overturning is not necessary to verify.Key words: retaining wall; stability against overturning; calculation
1006—2610(2016)05—0020—04
2016-03-21
姚存鍇 (1976- ),男,河南省清豐縣人,工程師,主要從事水利水電工程設計工作.
TU476.4
A
10.3969/j.issn.1006-2610.2016.05.005

