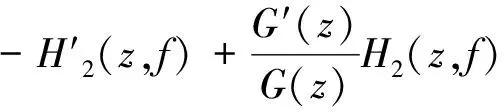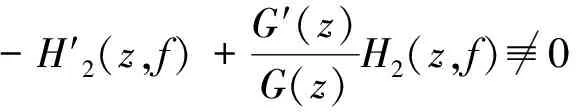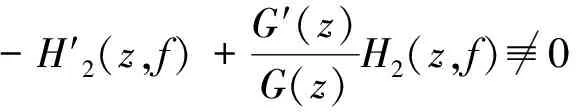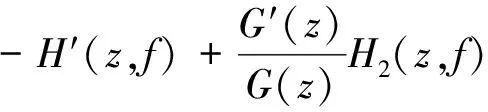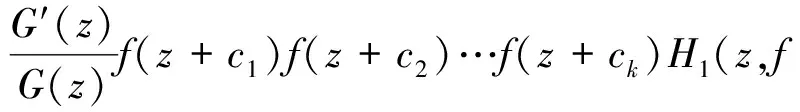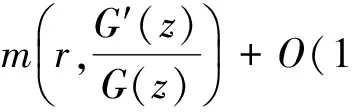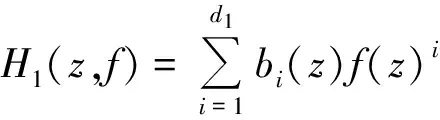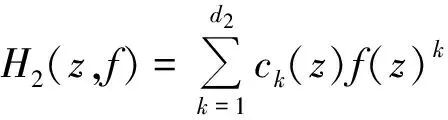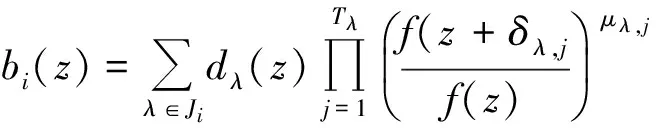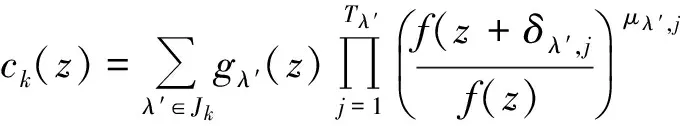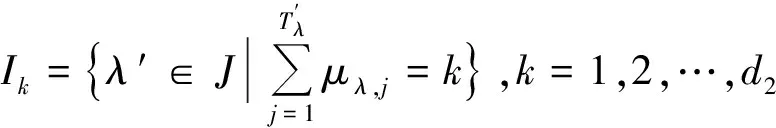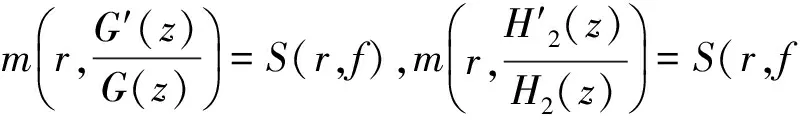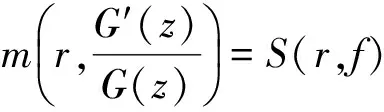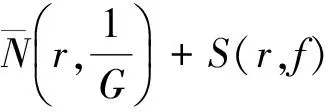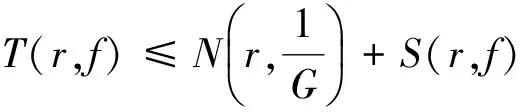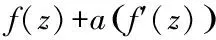一類超越亞純函數的差分多項式的值分布

石寧生， 金 瑾

(1.貴州工程應用技術學院 師范學院， 貴州 畢節 551700；2.貴州工程應用技術學院 數學系， 貴州 畢節 551700)

?

一類超越亞純函數的差分多項式的值分布

石寧生1， 金 瑾2*

(1.貴州工程應用技術學院 師范學院， 貴州 畢節 551700；2.貴州工程應用技術學院 數學系， 貴州 畢節 551700)

利用Nevanlinna的亞純函數的值分布理論，研究了超越亞純函數微分多項式的值分布理論， 討論了差分多項式的特征函數和零點，取得了一個結果.并且對差分多項式零點的一些經典結果建立了差分模擬．

超越亞純函數； 差分多項式;值分布； Nevanlinna理論

1 引言與主要結果

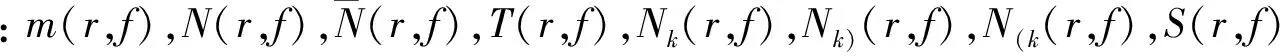
1959年，Hayman證明了下面的著名定理．

定理A[1]設f(z)為超越亞純函數，n為正整數，如果n≥3，則fn(z)f′(z)取每一個非零有窮復數無窮多次．

1969年，L.R.Sons證明了

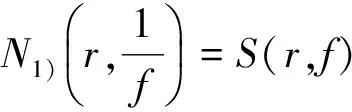
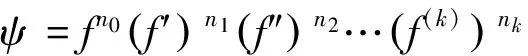
其中n0，n1，n2，…，nk是非負整數，并且k≥1，n0≥1，如果

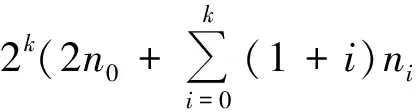
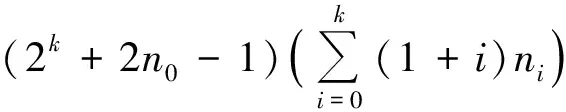
那么δ(a，ψ)<1，其中a≠0，∞．

b) f(z)是超越亞純函數，

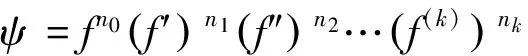
若nk≥1，n0≥2，且

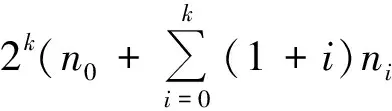
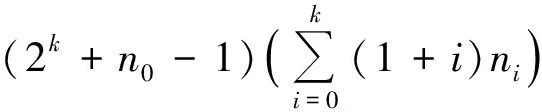
那么δ(a，ψ)<1，其中a≠0，∞．

1981年，N.Steinmetz進一步減弱了上述定理b)中條件，證明了

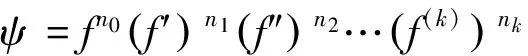
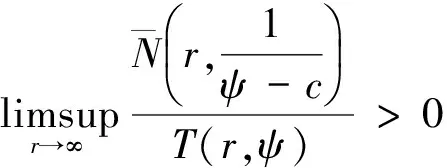
2002年，李偉和吳天毅對微分單項式進行了研究，給出了

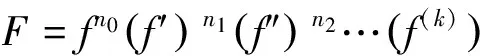
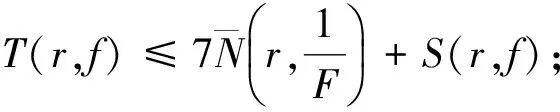
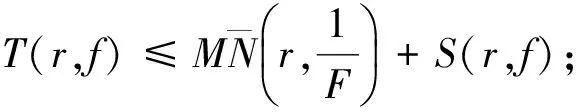
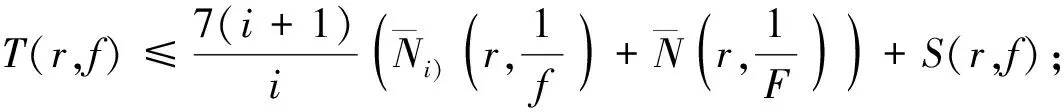
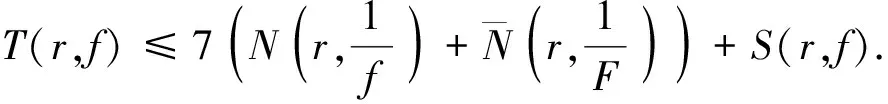
2007年，江秀海和高凌云得到如下結論．

定理E[5]設f(z)為平面內的超越亞純函數， a為任意非零復數，對任意的正整數m，i0，i1，…，in，λ=i0+i1+…+in，Δ=i1+2i2+…+nin，則當m≥λ+Δ+2時，

可取無窮多個零點．

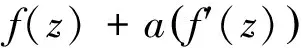
2012年，張然然和陳宗煊研究了亞純函數f(z)的差分多項式

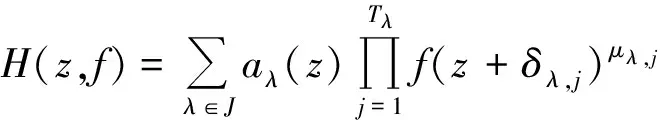
(1.1)

得到

定理G[7]設f(z)是有限級亞純函數，滿足N(r，f)=S(r，f)，設H(z，f)形若(1.1)的差分多項式，其中系數是為f(z)的小函數.且H(z，f)中僅有一個單項式具有最高次數degfH，則

H(z，f)=(degfH)T(z，f)+S(z，f)．

在本文中，令

f(z+ck)ik

(1.2)

其中,k≥1為整數，c1，c2，…，ck為相互不同的復常數，i1，i2，…，ik為非負整數，ai(z)為f(z)的小函數.記max{i1+i2+…+ik}=n=degfF(z)，則有

λ(G)=σ(G)=σ(f)

和

2 引理及其證明

對文獻[8]中的推論2.2做變形得到引理2.1．

引理2.1設f(z)是非常數有限級亞純函數，η1，η2是任意復常數，則

將引理2.1應用到[9，定理2.3]，可以得到如下引理2.2．

引理2.2設f(z)是方程U(z，f)P(z，f)=Q(z，f)的有限級超越亞純函數解，其中U(z，f)，P(z，f)，Q(z，f)都是f(z)的差分多項式，系數都是f(z)的小函數，且degfU=n，degfQ≤n，又設U(z，f)中僅有一個單項式具有最高次數，則m(r，P(z，f))=S(r，f)．

注 仔細考察引理2.2的證明過程可知，當P(z，f)，Q(z，f)是關于f(z)的微差分多項式且它們的系數aλ(z)滿足m(r，aλ)=S(r，f)時(此時不一定滿足T(r，aλ)=S(r，f)).任然可以得到引理2.2的結論.這里，我們稱V(z，f)為f(z)的微差分多項式，如果V(z，f)是關于f(z)，f(z)的導數， f(z)的位移以及f(z)位移導數的多項式，且系數為亞純函數．

應用到[10，定理2.1]，可以得到如下引理2.3．

引理2.3設f(z)是非常數有限級亞純函數，c≠0是任意復常數，則

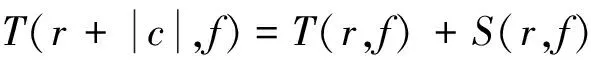
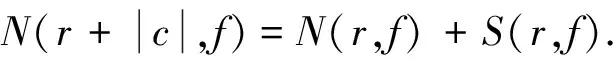
文獻[11，p66]得到:設f(z)是亞純函數，則對任意的c≠0，當r→∞時，不等式

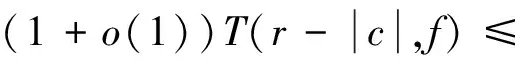
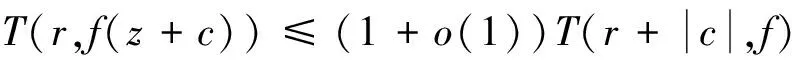
成立.由上述不等關系的證明過程知，上述不等關系對密指量也成立.由此及引理2.3容易得到下面引理2.4．

引理2.4設f(z)是非常數有限級亞純函數，c≠0是任意復常數，則

T(r，f(z+c))=T(r，f)+S(r，f)，

N(r，f(z+c))=N(r，f)+S(r，f)，

N(r，1/f(z+c))=N(r，1/f)+S(r，f)．

3 定理的證明

F(z)H1(z，f)=-H2(z，f)．

由于max{i1+i2+…+ik}=n=degfF(z)，即有degfH2(z，f)

m(r，H1)=S(r，f)和m(r，fH1)=S(r，f)，

(3.1)

由引理2.4及假設條件N(r，f)=S(r，f)，得到

N(r，H1)=S(r，f)和N(r，fH1)=S(r，f)，

(3.2)

所以由(3.1)和(3.2)有

T(r，H1)=S(r，f)和T(r，fH1)=S(r，f)，

(3.3)

微分

G(z)=F(z)H1(z，f)+H2(z，f)，

(3.4)

得到

G′(z)=F′(z)H1(z，f)+

F(z)H′1(z，f)+H′2(z，f)，

(3.5)

F′(z)H1(z，f)+F(z)H′1(z，f)-

(3.6)

G(z)=CH2(z，f)，

(3.7)

其中，C是非零常數，將(3.7)式帶入(3.4)式得到

F(z)H1(z，f)=(C-1)H2(z，f)，

(3.8)

-H′2(z，f)+G′(z)G(z)H2(z，f)≡0

(3.9)

將

f(z+c2)i2…f(z+ck)ik

和

代入(3.6)式，整理得到

f(z+c1)i1-1f(z+c2)i2-1…f(z+ck)ik-1E(z)=

(3.10)

其中

f(z+ck)H′1(z，f)-

(3.11)

再由(3.10)式和

得到

(3.12)

下面估計(3.12)中各項:

由于G(z)=F(z)H1(z，f)+H2(z，f)和degfH2(z，f)

degfG(z)

記degfH1=d1，degfH2=d2.類似于[9，定理2]的方法，將H1(z，f)和H2(z，f)改寫為

(3.13)

(3.14)

其中

(3.15)

(3.16)

由于H1(z，f)和H2(z，f)的系數dλ(z)和gλ(z)都是f(z)的小函數，故有

m(r，aλ)≤T(r，aλ)=S(r，f)，

m(r，gλ′)≤T(r，gλ′)=S(r，f)．

因此，由引理2.1知，對i=1，2，…，d1和k=1，2，…，d2有

m(r，bi(z))=S(r，f)

和

m(r，ck(z))=S(r，f)，

(3.17)

若degfH1=d1=1和degfH2=d2=1時有

H1(z，f)=b1(z)f(z)+b0(z)

和

H2(z，f)=c1(z)f(z)+c0(z)，

所以有

m(r，H1)≤m(r，f)+m(r，b1)+

m(r，b0)+O(1)=m(r，f)+S(r，f)，

m(r，H2)≤m(r，f)+m(r，c1)+

m(r，c0)+O(1)=m(r，f)+S(r，f)．

若degfH1=d1>1和degfH2=d2>1時，則(3.13)和(3.14)改寫為

H1(z，f)= f(z)(bd1(z)fd1-1(z)+…+

b1(z))+b0(z)，

H2(z，f)= f(z)(cd2(z)fd2-1(z)+…+

c1(z))+c0(z)．

所以有

m(r，H1)≤m(r，f)+m(r，(bd1(z)fd1-1(z)+

…+b1(z))+b0(z))+S(r，f)，

(3.18)

m(r，H2)≤m(r，f)+m(r，(cd2(z)fd2-1(z)+

…+c1(z))+c0(z))+S(r，f).

(3.19)

由(3.18)和(3.19)以及歸納法知

m(r，H1)≤d1m(r，f)+S(r，f)，

(3.20)

m(r，H2)≤d2m(r，f)+S(r，f).

(3.21)

因此由上述(3.13)-(3.21)可得到

m(r，G)≤(n+degfH1)m(r，f)+S(r，f)，

(3.22)

m(r，G)≤(n+degfH2)m(r，f)+S(r，f)，

(3.23)

由已知N(r，f)=S(r，f)得到N(r，G)=S(r，f)和N(r，H2)=S(r，f)，所以

T(r，G)≤(n+degfH1)T(r，f)+S(r，f)，

(3.24)

T(r，H2)≤(degfH2)T(r，f)+S(r，f).

(3.25)

由以上兩式可得S(r，G)=S(r，f)和S(r，H2)=S(r，f).所以由

可得

(3.26)

m(r，E)=S(r，f)．

由(3.11)和N(r，f)=S(r，f)，得到

故

由上式和第一基本定理得到

(3.27)

由定理G知

T(r，f(z+c1)i1-1f(z+c2)i2-1…f(z+ck)ik-1)≤

(n-k-1)T(r，f)+S(r，f)，

又由N(r，f)=S(r，f)得

N(r，f(z+c1)i1-1f(z+c2)i2-1…f(z+ck)ik-1)=S(r，f)．

所以

m(r，f(z+c1)i1-1f(z+c2)i2-1…f(z+ck)ik-1)=(n-k-1)T(r，f)+S(r，f).

(3.28)

由(3.12)，(3.13)以及(3.26)-(3.28)得到

(n-k-1)T(r，f)+S(r，f)≤

由上式及假設條件n-k-1>degfH2得到

(3.29)

所以，G(z)有無窮多個零點，由(3.24)和(3.29)得到λ(G)=σ(G)=σ(f)和

[1] HAYMAN W K.Picardvalue of meromorphic function and their derivatives[J].Ann Math,1959,70： 9-42．

[2] SONS L R.Defficiencies of monomials[J].Math Z，1969，111：53-68．

[3] Steinmetz N.Uber die nullstellens von differential polynomen[J].Math Z，1981， 176：255-264．

[4] 李 偉， 吳天毅. 關于一般微分單項式的值分布[J].系統科學與數學，2002， 22(1):58-66．

[7] 張然然， 陳宗煊. 亞純函數差分多項式的值分布[J].中國科學，2012， 42(11)：1115-1130．

[8]HALBURDRG，KORHONENRJ.Differenceanalogueofthelemmaonthelogarithmicderivativewithapplicationstodifferenceequations[J].JMathAppl，2006， 314：477-487．

[9]LAINEI，YANGCC.Clunietheoremsfordifferenceandq-differencepolynomials[J].JLondonMathSoc， 2007， 76：556-566．

[10] HALBURD R G, KORHONEN R J.Finite-order merom0rphic solutions and the discrete Painleve equations[J].Proc London Math Soc， 2007， 94：443-474．

[11] GOL’DBERG A A，OSTROVSKII I V.Distribution of Values of Meromorphic Functions[M].Moscow：Nau-ka，1970．

[12] 金 瑾. 高階線性微分方程解的二階導數的不動點[J].數學的理論與應用， 2007， 27(4)：107-113．

[13] 金 瑾. 一類高階齊次線性微分方程亞純解的超級及其不動點[J].華中師范大學學報(自然科學版)， 2011， 45(1):18-22．

[14] 金 瑾. 高階微分方程解與其小函數的關系[J].高校應用數學學報， 2013， 28(1):43-51．

[15] 金 瑾. 關于一類高階齊次線性微分方程解的增長性[J].中山大學報， 2013， 52(1):51-55．

[16] 金 瑾. 高階微分方程解的超級的輻角分布[J].數學的實踐與認識， 2008， 32(12):178-187．

Value distribution of difference polynomials of transcendental meromorphic functions

SHI Ningsheng1, JIN Jin2

(1.Normal College, Guizhou University of Engineering Science, Bijie, Guizhou 551700;2.Department of Mathematics, Guizhou University of Engineering Science, Bijie, Guizhou 551700)

In this paper, the value distribution of differential polynomials on meromorphic function was studied by using Nevanlinna value distribution theory on meromorphic function. The results of differential polynomials were obtained, and difference analogues are established on some classical results of the zeros from differential polynomials.

transcendental meromorphic function；difference polynomial；value distribution；Nevanlinna theory

2016-02-19.

貴州省科學技術基金項目(2010GZ43286)； 貴州省科學技術基金項目(2012GZ10526).

1000-1190(2016)04-0481-05

O174.52

A

*E-mail: jinjin62530@163.com.