Victor-Carmen混沌系統的投影同步

陳昌忠， 何 平

(四川理工學院 自動化與電子信息學院， 四川 自貢 643000)

?

Victor-Carmen混沌系統的投影同步

陳昌忠， 何 平*

(四川理工學院 自動化與電子信息學院， 四川 自貢 643000)

基于小增益理論，本文研究了一個新型Victor-Carmen混沌系統的投影同步問題.一個更為一般的達成投影同步的充分條件被推得.數值仿真驗證了本文所設計的投影同步的有效性.

Victor-Carmen混沌系統; 投影同步; 小增益理論

[11]中，Victor Grigoras和Carmen Grigoras在線性振蕩環節的基礎上，通過引入非線性動態，得到了一個新型的混沌系統，如下所示：

(1)

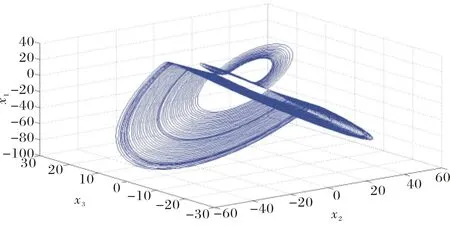
圖1 Victor-Carmen混沌系統(1)的相圖Fig.1 Phase diagram of the Victor-Carmen chaotic system (1)

其中，x=[x1， x2， x3]T是Victor-Carmen混沌系統的狀態變量，a， b， α， β， γ是系統參數.

設定參數a=5， b=9， α=50， β=20， γ=4.1時，系統(1)表現出復雜的混沌性.當取初始條件為x(0)=[5， 1，-5]T時，Victor-Carmen混沌系統(1)的相圖如圖1所示.

通過計算可得系統的平衡點為

O1(0，0，0)、O2(-0.3468，0.0628，0.01104)、

O3(-2.064，1.382，0.02987)、

O4(0.2500，-0.002231，2'242)、

O5(4.787，2.948，-0.03248).

2 同步控制器設計

將系統(1)看作驅動系統，構造響應系統如下所示.

(2)

定義誤差向量

(3)

則誤差動力學系統可以寫為

(4)

在不同初始條件下，在沒有控制器u作用下，響應系統和驅動系統的軌跡將不能達成同步.然而，在合適的同步控制器作用下，響應系統(2)和驅動系統(1)在任何初始條件下達成投影同步，為了實現這一目標，選擇控制器如下所示.

(5)

其中，參數k是稍后確定的投影同步控制器增益.

3 主要定理

定理若控制器增益k滿足條件

(6)

則驅動系統(1)和響應系統(2)可以在同步控制器(5)的作用下達到關于標量因子η的投影同步，其中ε1和ε2是充分小的正常數，即0<ε1<1，0<ε2<1.

證明將同步控制器(5)代入誤差動力系統(4)可得

(7)

根據一階線性微分方程解的結構易知

e1(t)=exp(-t)e1(0).

(8)

則有

(9)

因此系統(7)可以簡化為

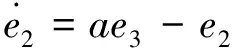
(10-1)

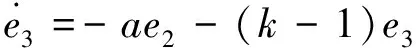
(10-2)

其中，將系統(10-1)、(10-2)看作兩個系統的互聯形式，將e2和e3分別視為子系統(10-1)的狀態和輸入，并對其構造Lyapunov函數為

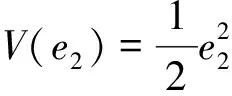
(11)

將Lyapunov函數(11)沿系統(10-1)微分可得

(12)

選擇

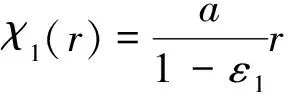
(13)

其中，若ε1(0<ε1<1)是一個充分小的正常數，

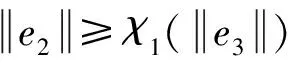
(14)

則將(14)式代入(12)式可得

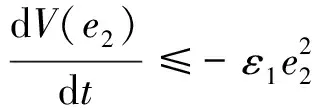
(15)

取K∞函數

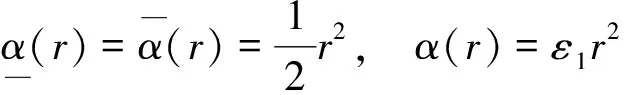
(16)

則函數(11)是正則且正定的(proper & positive)，因此，函數(11)是系統(10-1)的ISS-Lyapunov函數，系統(10-1)是ISS的，且有

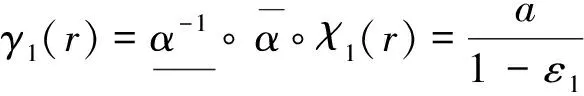
(17)

將e3和e2分別視為子系統(10-2)的狀態和輸入，并對其構造Lyapunov函數為

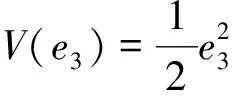
(18)

將Lyapunov函數(18)給系統(10-2)微分可得

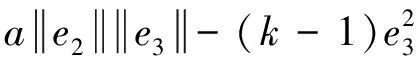
(19)

選擇

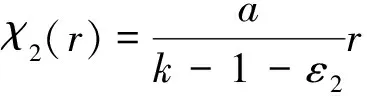
(20)

其中，ε2(0<ε2<1)的一個充分小的正常數.假設

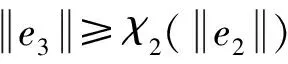
(21)

則有

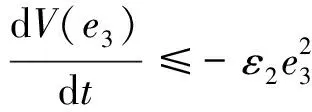
(22)

同理取K∞函數

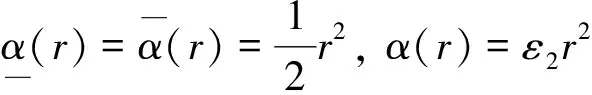
(23)

則函數(18)是正則且正定的(proper & positive)，函數(18)是系統(10-2)的ISS-Lyapunov函數，系統(10-2)是ISS的，且有

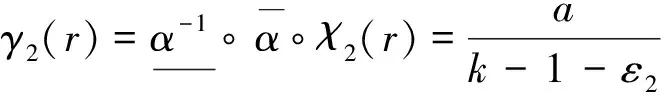
(24)

因此，根據(17)和(24)式可得

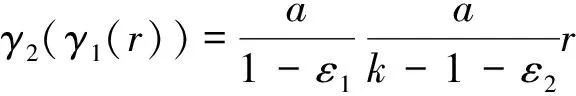
(25)

由條件(6)可知

γ2(γ1(r))≤r，?r>0，

(26)

由小增益定理可知，系統(10)的平衡點是全局漸近穩定的，則有

(27)

由(9)和(27)知，誤差系統(7)是全局漸近穩定的，則在同步控制器(5)的條件下，驅動系統(1)和響應系統(2)達成關于標量因子的投影同步.證畢.

4 系統仿真

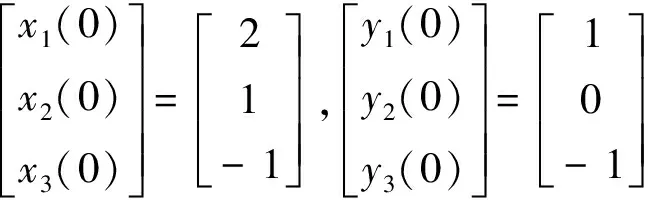
選擇標量因子η=3，則初始誤差為

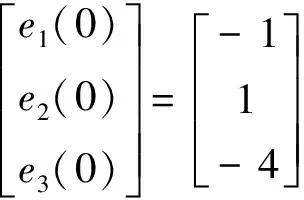
驅動系統(1)和響應系統(2)在控制器u的作用下投影同步誤差的動態響應曲線如圖2-圖4所示.

圖2～圖4 表示了驅動系統(1)和響應系統(2)的投影同步誤差，可以看出同步誤差很快收斂到零.

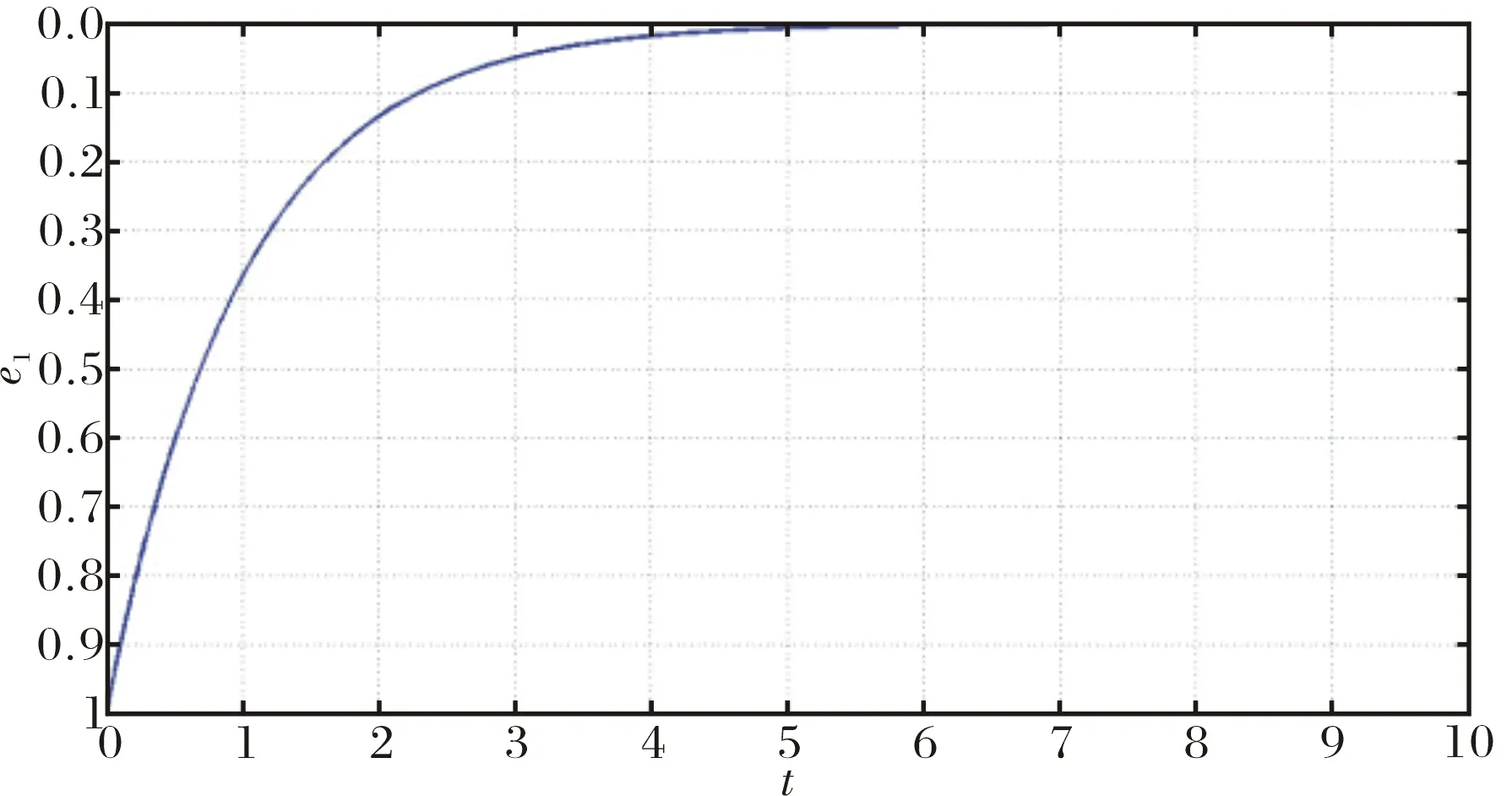
圖2 驅動系統(1)和響應系統(2)的投影同步誤差e1Fig.2 PS error e1of drive system (1) and response system (2)

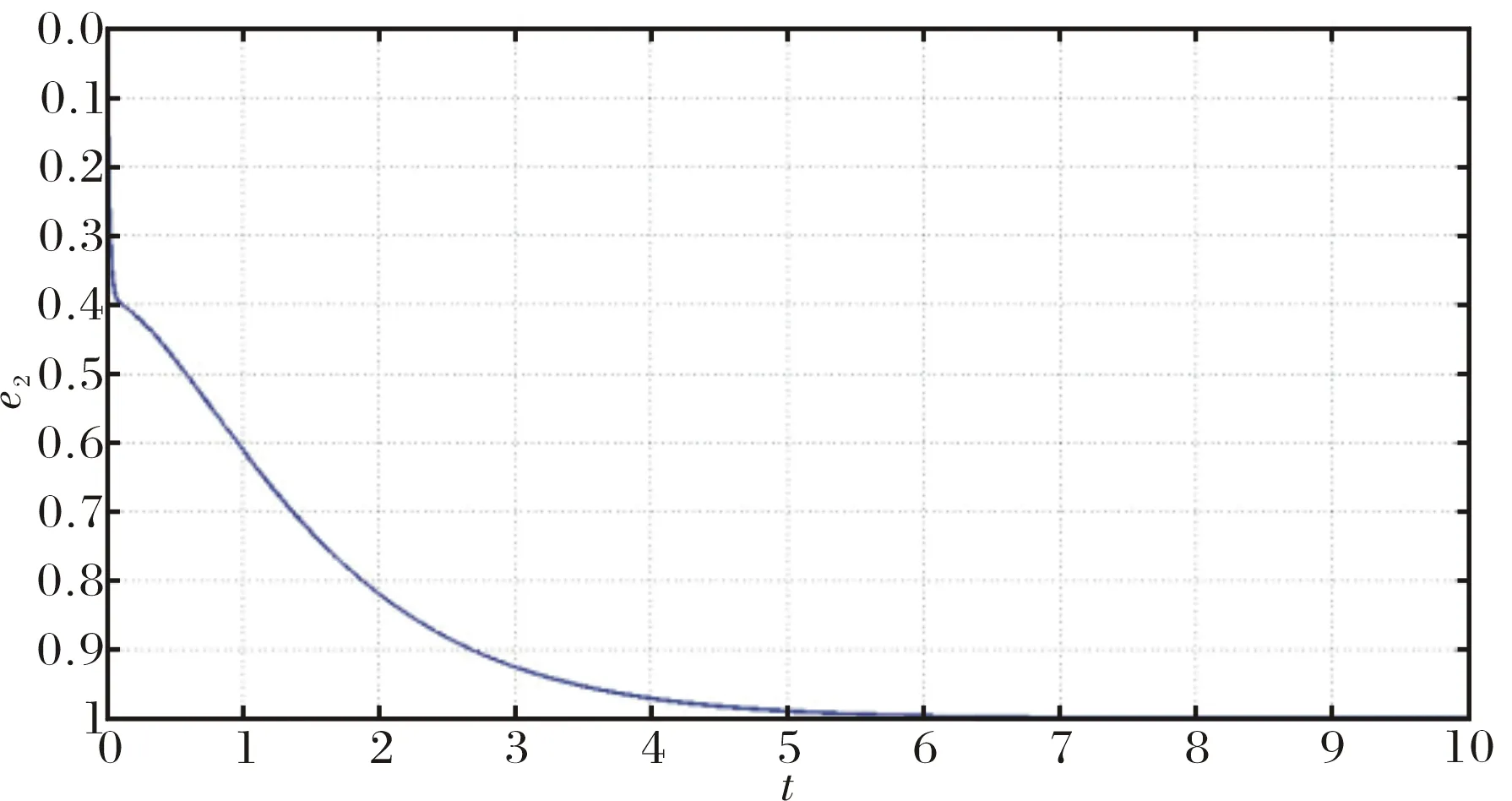
圖3 驅動系統(1)和響應系統(2)的投影同步誤差e2Fig.3 PS error e2 of drive system (1) and response system (2)

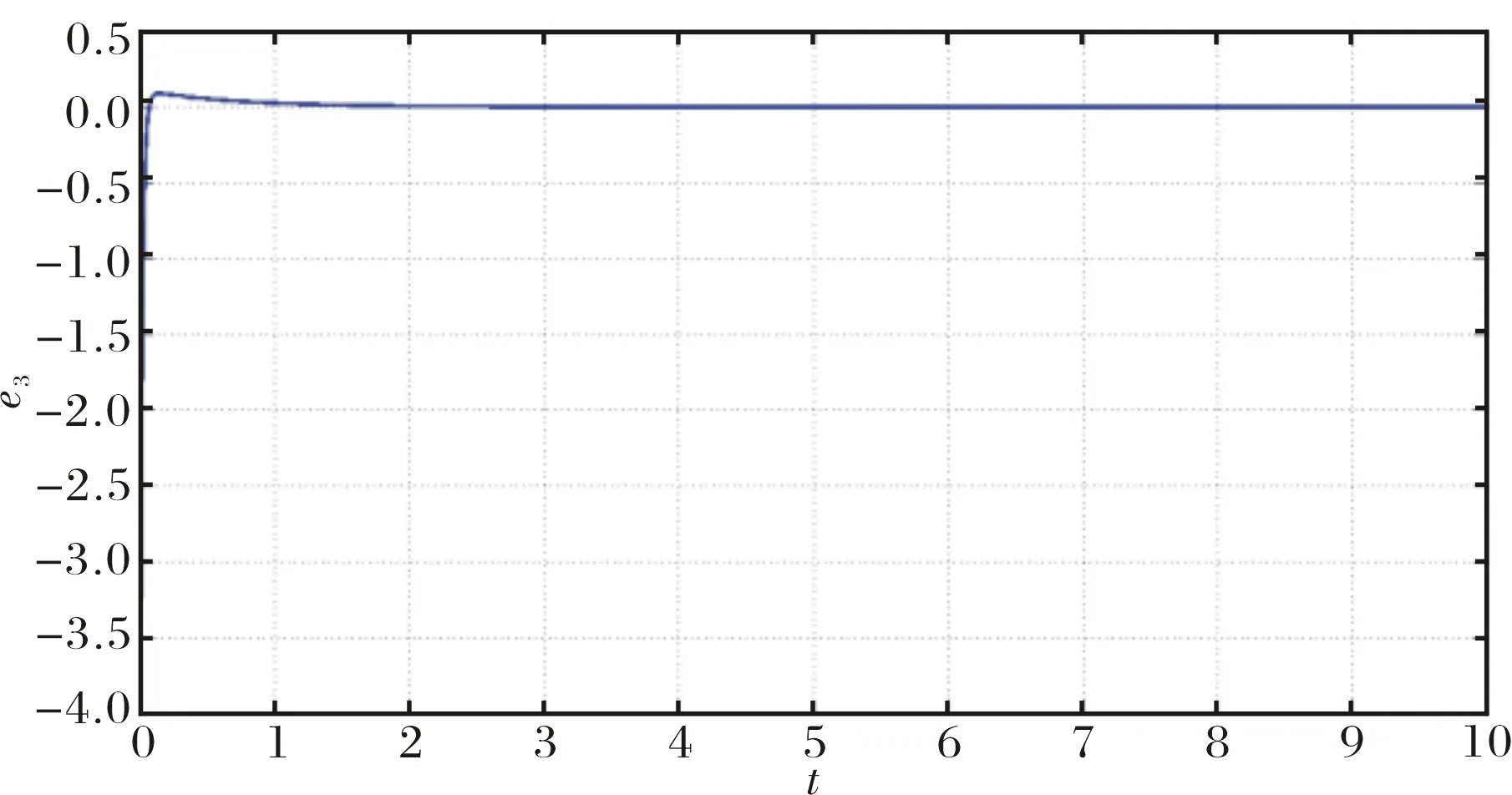
圖4 驅動系統(1)和響應系統(2)的投影同步誤差e3Fig.4 PS error e3 of drive system (1) and response system (2)

本文的投影同步包含了已有的完全同步和反同步，即，當η=1時，即為完成同步，η=-1時，即為反同步.

5 總結

本文研究了一個新型三維混沌系統的投影同步問題，其創新性在以下兩方面：1)簡要分析了Victor-Carmen混沌系統的特性；2)基于小增益定理達成了其投影同步問題，包含了反同步與完全同步.最后，數值仿真表明了本文方法的有效性.

參考文獻：

[1] BANERJEE R， PADMANABAN E， DANA S K. Control of partial ynchronization in chaotic oscillators[J]. PRAMANA-Journal of Physics， 2015， 84(2): 203-215．

[2] ISRAR A， AZIZAN B S， ADYDA B I， et al. Global chaos synchronization of new chaotic system using linear active control[J]. Complexity， 2014， 21(1): 379-386．

[3] HE P， JING C G， FAN T， et al. Robust decentralized adaptive synchronization of general complex networks with coupling delayed and uncertainties [J]. Complexity， 2014， 19(3): 10-26．

[4] HE P， ZHANG Q L， JING C G， et al. Robust exponential synchronization for neutral complex networks with discrete and distributed time-varying delays: A descriptor model transformation method[J]. Optimal Control Applications and Methods， 2014， 35(6):676-695．

[5] HE P， JING C G， FAN T， et al. Synchronization of general complex networks via adaptive control schemes [J]. PRAMANA-Journal of Physics， 2014， 82(3): 499-514．

[6] HE P， MA S H， FAN T. Finite-time mixed outer synchronization of complex networks with coupling time-varying delay[J]. Chaos， 2012， 22(4): 043151(1-11)．

[7] CHEN C Z， FAN T， WANG B R， et al. Feedback linearization synchronization of unified chaotic systems [J]. Journal of Applied Nonlinear Dynamics， 2014， 3(2): 173-186．

[8] FAN T， CHEN C Z， REN X H， et al. Adaptive synchronization of delayed Chen chaotic system[J]. Discontinuity， Nonlinearity and Complexity， 2014， 3(4): 367-378．

[9] 何 平， 任小洪， 李風煥. 不確定性統一混沌系統的魯棒鎮定[J]. 華中師范大學學報(自然科學版) ， 2012， 46(1): 35-39．

[10] CHEN C Z， FAN T， WANG B R. Inverse optimal control of hyperchaotic finance system[J]. World Journal of Modelling and Simulation， 2014， 10(2): 83-91．

[11] GRIGORAS V， GRIGORAS C. A Novel Chaotic System for Random Pulse Generation[J]. Advances in Electrical and Computer Engineering， 2014， 14(2): 109-112．

[12] JIAN X. Projective synchronisation of a new chaotic system via small-gain theorem[J]. International Journal of Systems Science， 2012， 43(4): 741-747.

Projective synchronization of the Victor-Carmen chaotic system

CHEN Changzhong, HE Ping

(School of Automation and Electronic Information, Sichuan University of Science & Engineering, Zigong, Sichuan 643000)

The projective synchronization between two identical Victor-Carmen chaotic systems is investigated. Moreover, the general sufficient condition to achieve projective synchronization is obtained by using the small-gain theorem. Numerical simulation is then provided to show the effectiveness and feasibility of the proposed method.

Victor-Carmen chaotic system； projective synchronization； small-gain theorem

2015-11-17.

四川省教育廳基金項目(14ZA0203、14ZB0210)；四川理工學院科研基金項目(2014PY14)；人工智能四川省重點實驗室基金項目(2013RYJ01、2014RYY02)；企業信息化與物聯網測控技術四川省高校重點實驗室開放基金項目(2014WYJ01、2013WYY06).

1000-1190(2016)04-0521-04

O415.5

A

1 Victor-Carmen混沌系統

*通訊聯系人. E-mail: pinghe@suse.edu.cn.

過去30年，由于在各個領域的廣泛應用，對混沌同步的研究受到了廣大學者的親睞[1-2]，相關報道層出不窮[3-6]，諸多同步控制方法相繼被報道，譬如微分幾何方法[7]，滑模控制方法[8]，魯棒控制[9]，最優控制方法[10]等，這些混沌同步在生物、化學、醫藥、信息、電子、保密通信等領域中都有廣泛應用.在諸多同步體制中，投影同步是最為感興趣的問題之一.最近，Victor Grigoras和Carmen Grigoras通過在線振蕩環節的基礎上引入非線性動態，得到了一個新型的三維混沌系統[11]，而并沒有對其同步問題予以研究.本文則基于小增益定理[12]研究其投影同步問題，從后文的分析可以看出，本文的同步控制器只需要確定額外的一個參數，其分析也是簡潔的.