汽車制動系統可靠性預測的模糊神經網絡研究

倪 泉 葛友華 王 斌

(常州大學機械工程學院1，江蘇 常州 213164；鹽城工學院機械工程學院2，江蘇 鹽城 224001)

?

汽車制動系統可靠性預測的模糊神經網絡研究

倪 泉1葛友華2王 斌2

(常州大學機械工程學院1，江蘇 常州 213164；鹽城工學院機械工程學院2，江蘇 鹽城 224001)

計時傳統模糊神經網絡算法在汽車制動系統(ABS)可靠性預測中存在預測精度不高、誤差較大等問題，提出了一種基于優化隸屬函數的改進模糊神經網絡算法。采用偏移優化方法對模糊控制算法的隸屬函數進行改進;引入粒子群算法進行自適應慣性權重的尋優能力、收縮因子的收斂速度優化;最后與模糊神經網絡算法融合，調整原算法的中心值、寬度值和連接權值，避免原算法在汽車制動系統可靠性預測中陷入局部最小值。仿真實驗表明，改進的模糊神經網絡算法具有比傳統神經網絡算法和模糊控制算法更小的預測誤差。

汽車制動系統(ABS) 可靠性預測 模糊神經網絡 粒子群算法(PSO) 函數優化

0 引言

汽車的安全性能已經成為人們重視的主要方面[1]。汽車安全性能研究起步較早，首先應用于實際的是汽車制動系統(automotive braking system,ABS)，接著是防滑系統(acceleration slip regulation,ASR)、車身電子穩定系統(electronic stability program，ESP)等[2-3]。但是，交通事故依然頻發，汽車安全性能仍需要提高[4]。

從汽車制動系統可靠性預測研究來看，涌現出了Monte-Carlo 法、Bayes法、故障模式、影響和危害性分析(failure mode,effects and criticality analysis，FMECA) 法和故障樹分析(fault tree analysis，FTA)法等[5-10]。蔡駿宇提出基于IRAS 的汽車故障檢測模型，該模型一定程度上對汽車安全性能進行了檢測[6]。Che Yejun等建立了基于故障樹法的汽車發動機可靠性分析模型[7]。劉穎提出了基于最大熵試驗法的小型發動機安全性能預測模型[9]。張士峰等對小子樣系統可靠度評估方法進行了一定的研究[11]。

針對以上算法準確性不足的問題，設計了一種模糊神經網絡算法，采用模糊控制對神經網絡算法進行誤差的控制，以提高預測的準確性。

1 模糊神經網絡模型的局限性

對于汽車制動系統的可靠性預測，目前用的最多的是模糊神經網絡模型，其模型的構建方法如下所示。

第0層：將汽車制動系統傳遞的各個參數作為模糊神經網絡中每個神經元的值，即神經元的輸入值：

(1)

此層的神經元數即汽車制動系統傳遞的參數個數。

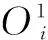
(2)

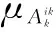
(3)

或

(4)

第2層：每個神經元是一個標以∏的固定神經元，它的輸出是所有制動系統參數輸入信號的積：

(5)

式中:第i個制動系統參數神經元的輸入相當于第i條可靠性預測的條件，其輸出就是可靠性預測的指標。其中，i=1,2,...,m，m是可靠性預測指標數。

第3層：計算輸出。

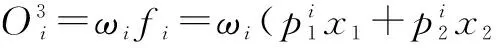
(6)

第4層：求和。

(7)

第5層：歸一化。

(8)

從上述基于模糊神經網絡的汽車制動系統可靠性預測模型中可以看出，雖然能夠成功地對汽車制動系統進行可靠性評估，但是模糊神經網絡本身存在的問題還是沒有得到妥善的處理。所以，必須對模糊神經網絡在數據較大時容易進入局部最優的問題進行優化。

2 模糊神經網絡算法的優化

2.1 隸屬函數的優化

對于離散論域隸屬函數，本文采用偏移優化的方法對其改進。如式(9)所示，有3個參數a、b和c。

(9)

初始隸屬函數的參數可由式(8)～式(10)構成。其中，xmax和xmin為x的最大值和最小值；mf_n為x對應的隸屬函數的個數。

(10)

b0=2

(11)

c是隸屬函數的中心。首先，x的每個隸屬函數的初始ci在[xmin,xmax]區間內平均產生，即：

(12)

然后，每個參數產生一個隨機的偏移量。

a1=a0×Ra

(13)

b1=b0×Rb

(14)

式中：Ra、Rb為一個大于0的有一定范圍的隨機數，實際上a和b的變化范圍可以小一點。

(15)

(16)

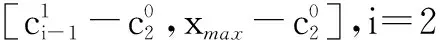
2.2 基于改進粒子群的模糊神經網絡

因為傳統的模糊神經網絡算法往往會出現局部最小的問題，本文引入粒子群算法。一般的粒子群算法的全局收斂能力無法達到模糊神經網絡算法的需求，所以本文首先對粒子群算法進行改進。

① 基于自適應慣性權重的尋優能力優化。

一般的粒子群算法中，慣性權重w代表了粒子對其父代飛行速度的作用程度，所以如果調正慣性權重的數值，就可以控制算法的尋優能力。

基于此，本文提出了對慣性權重進行自適應優化，如下式所示：

(17)

式中：Tmax為最大的迭代次數；wini為最初的慣性權重；wend為粒子進化到最大程度時的慣性權重。

一般情況下，選取wini=0.9、wend=0.4時，算法可以表現出更好的性能。

② 基于收縮因子的粒子收斂速度優化。

在對慣性權重進行調整的基礎上，本文還引入收縮因子對粒子的收斂速度進行了優化。基于收縮因子的粒子速度及位置的表達式為：

vid=χ[vid+c1r1(pid-xid)+c2r2(pgd-xid)]

(18)

其中，收縮因子取值公式如下：

(19)

式中：k的取值范圍為φ=c1+c2，并且φ>4。

③ 尋優范圍限定。

為了使粒子群算法能更好地應用于模糊神經網絡，本文對粒子群算法進行范圍的限定，設最優解集的大小為B。

首先，將迭代過程中種群的最優解全部都存儲到B當中，得到B值；再計算出最優解擁擠距離，按照大小進行排列；接著，按照全局當中的極值來選擇策略B當中的解值；然后將這個解當作全局最優解，并對粒子的速度進行更新，如下式所示：

(20)

(21)

在此基礎上，對粒子的位置進行控制，控制范圍為：

(22)

最后，將優化后的粒子群算法引入模糊神經網絡算法中，對模糊神經網絡的輸入樣本用改進粒子群算法進行聚類優化，得到隸屬度中心，從而提升模糊神經網絡的尋優能力和尋優速度。

基于改進粒子群算法的模糊神經網絡算法中，每一個粒子和每一組聚類中心為一對一映射，用G[P]表示，其中G包含了粒子的各個屬性，P表示粒子的數量。G[P]的適應度函數如下式所示。

(23)

式中：x為每個樣本到聚類中心的距離的總和；c為聚類中心；θ為數據集合；J為聚類類別的總數。

由傳統的算法可知，如果與粒子群算法融合，就必須對中心值參數、寬度值參數和連接權值進行調整。本文的調整策略如下。

① 采用本文提出的改進粒子群算法對隸屬度函數中心進行求解。

② 用確定的隸屬度函數中心來對寬度值參數進行求解：

(24)

式中：c為聚類中心；θ為樣本集合；M為樣本數量。

③ 用偽逆法對連接權值進行求解，如下式所示。

W=S-1T

(25)

式中:S為輸出矩陣；T為期望矩陣。

3 算法性能仿真

為了驗證本文提出的改進算法的有效性，對其進行仿真試驗。本次仿真試驗的汽車為大眾帕薩特，型號為2014款1.4T手動尊雅版，發動機型號為EA111，最大功率為96 kW，排量為1 390 mL，進氣形式為渦輪增壓，汽缸數為4個。

首先用改進的模糊神經網絡模型(FNN)對汽車制動系統中的制動器參數預測的誤差進行仿真試驗，并與模糊控制算法(FC)和神經網絡算法(NN)進行對比，結果如表1和圖1、圖2所示。

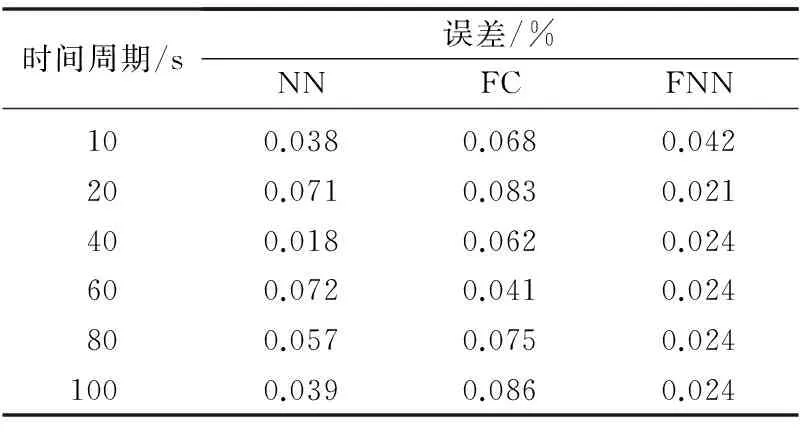
表1 誤差對比統計表

表1中，NN為神經網絡，FC為模糊控制，FN為模糊神經網絡。

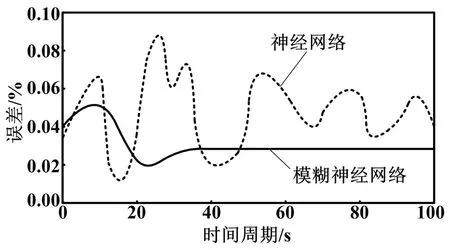
圖1 改進模糊神經網絡與傳統神經網絡誤差對比

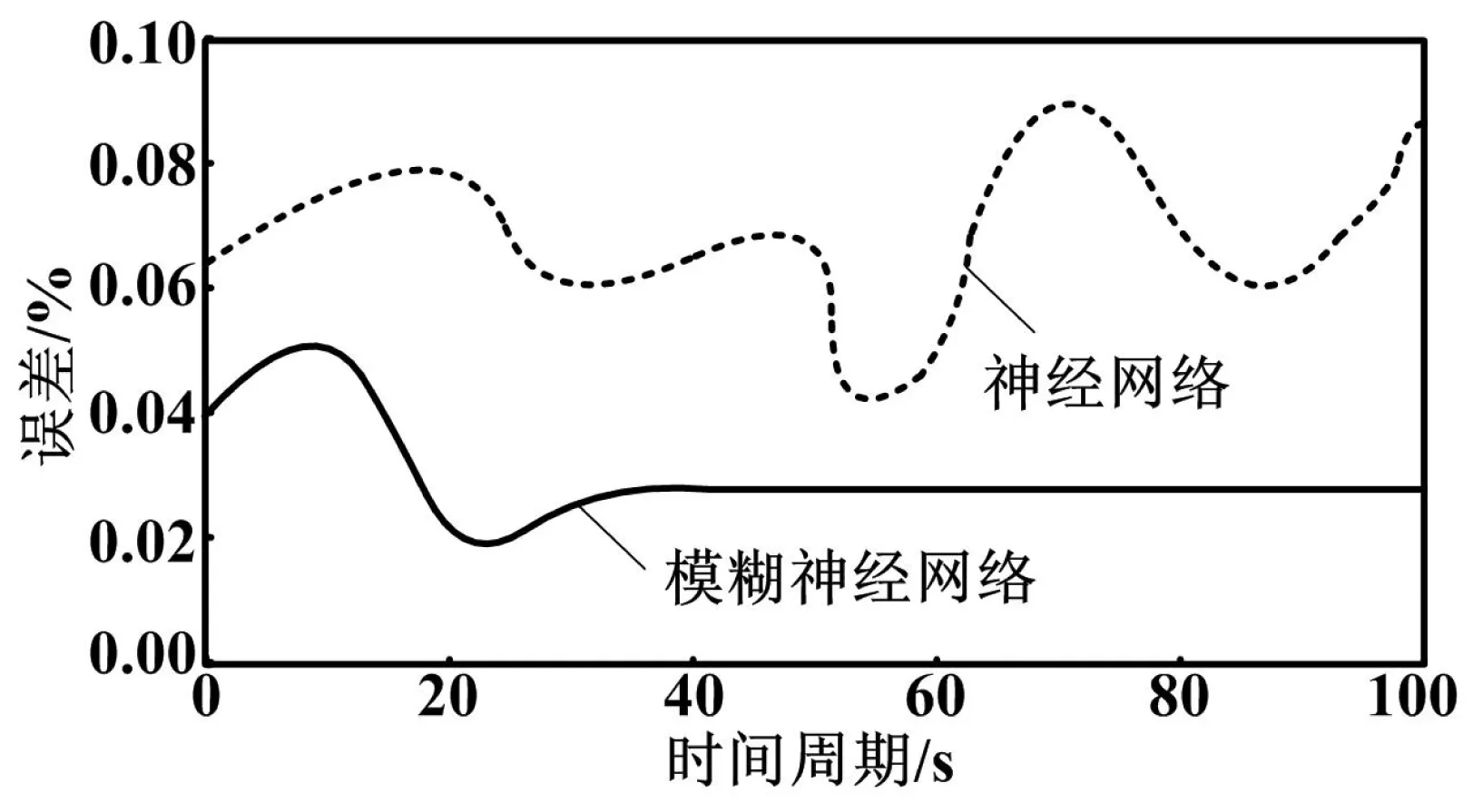
圖2 改進模糊神經網絡與模糊控制算法誤差對比

然后采用人工神經網絡算法、模糊控制算法和本文提出的改進模糊神經網絡算法對汽車制動系統進行整體性可靠性預測，得出汽車制動的安全系數，結果如圖3和表2所示。

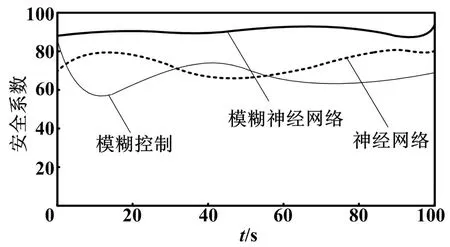
圖3 三種算法對汽車制動安全系數的仿真結果

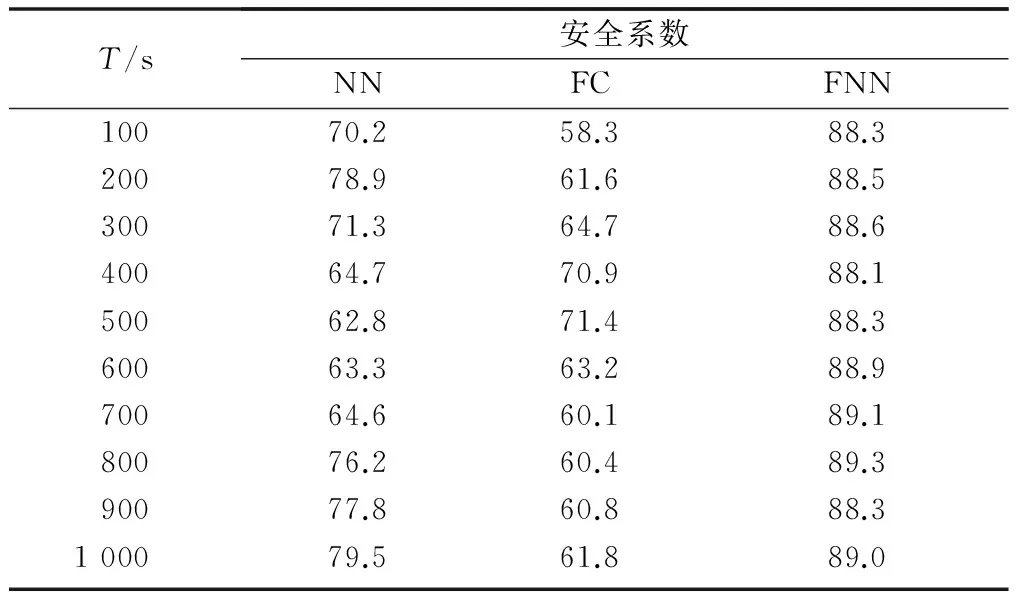
表2 汽車制動安全系數分析

最后，在試驗條件相同的情況下，對人工神經網絡算法、模糊控制算法和本文提出的改進模糊神經網絡算法進行穩定性分析，結果如表3和圖4所示。

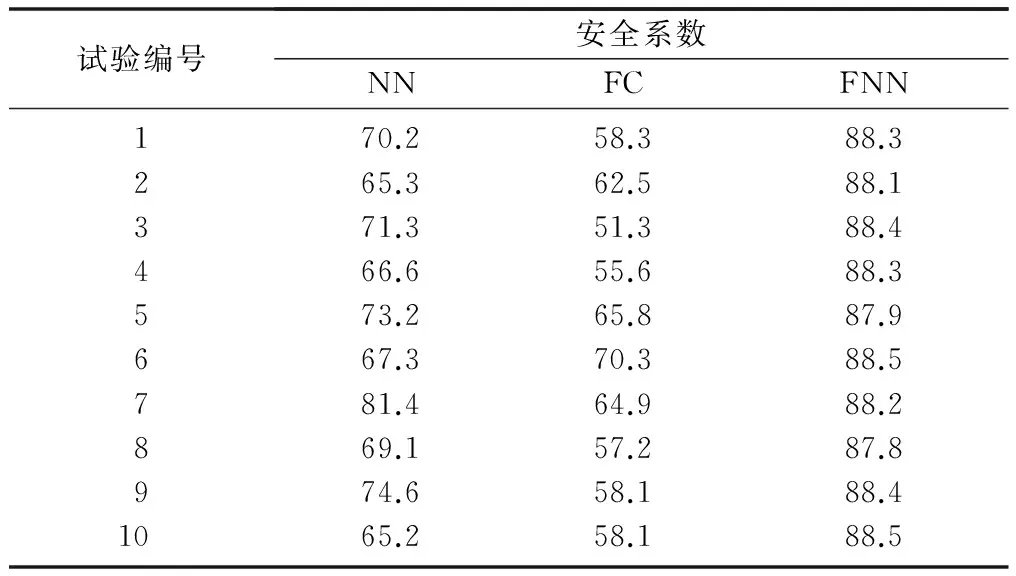
表3 汽車制動安全系數分析

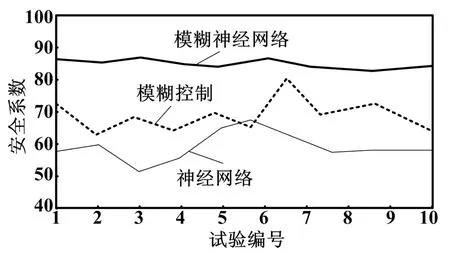
圖4 三種算法對汽車制動安全系數的仿真結果

從仿真結果可以看出，本文提出的基于優化隸屬函數和改進粒子群算法的模糊神經網絡算法利用改進的粒子群算法控制了預測的穩定性，比其他兩種算法對汽車制動系統可靠性預測的效果要好，大大降低了預測的誤差，提高了汽車制動系統的安全性能。

4 結束語

汽車制動系統的安全性能歷來是人們最為關心的問題之一。本文根據汽車制動系統，提出了汽車制動系統可靠性預測算法。從仿真結果可以看出，本文提出的基于汽車制動系統可靠性預測的改進模糊神經網絡算法的誤差遠遠小于傳統算法，證明本文的改進策略切實有效。

[1] 初亮,蔡健偉.汽車制動防抱死系統分離路面的控制策略[J].吉林大學學報：工學版,2014(2):287-291.

[2] Gong X W.Braking force distribution of electric vehicles based on braking stability[J].Journal of Chang'an University：Natural Science Edition,2014,34(1):103-108.

[3] 唐家棟,劉志遠.汽車制動壓力的切換PI控制方法研究[J].汽車技術,2014(3):24-30.

[4] 趙韓,胡金芳.混合動力汽車制動穩定性分層協調控制策略[J].汽車工程,2014,36(1):93-100.

[5] Wang M J.Multiple objective decision design for disk brake based on non-cooperative game theory[J].Modern Manufacturing Engineering,2014(1):9-14.

[6] 蔡駿宇.基于MEMS的汽車制動性能道路測試技術研究[J].電子技術應用,2013,39(6):77-80.

[7] Che Y J.Analysis and research on automotive brake performance[J].Science Technology and Engineering,2013(6):1695-1699.

[8] Zhang H Y.Automobile anti-lock braking system control strategy simulation[J].Manufacturing Automation,2013,34(18):87-90.

[9] 劉穎.汽車制動優化控制方法研究[J].計算機仿真,2012,29(8):340-343.

[10]尹夢晨.基于CFD分析的汽車空氣動力學制動研究[J].合肥工業大學學報：自然科學版,2011,34(3):326-330.

[11]張士峰,蔡洪.小子樣條件下可靠性試驗信息的融合方法[J].國防科技大學學報,2004,26(6):25-27.

Research on the Fuzzy Neural Network used for Reliability Prediction of Automotive Braking System

To overcome the disadvantages of traditional fuzzy neural network algorithm in reliability prediction of automotive braking system,e.g.,low prediction accuracy and large error,etc.,the improved fuzzy neural network algorithm by optimizing membership function is proposed.By adopting the method of offset optimization,the membership function of fuzzy control algorithm is improved,and the particle swarm algorithm is introduced to optimize adaptive inertia weight optimization capability and convergence rate of contraction factor,finally the fuzzy neural network algorithm is merged to adjust the central value,width value,and connection weight value of original algorithm,to avoid falling into local minimum in reliability prediction of automotive braking system with original algorithm.The simulation shows that the improved fuzzy neural network algorithm offers smaller prediction error than traditional neural network algorithm.

Automotive braking system(ABS) Reliability prediction Fuzzy neural network Particle swarm optimization(PSO) Function optimization

江蘇省自然科學基金面上資助項目(編號：BK20131221)。

倪泉(1987-)，男，現為常州大學機械制造及其自動化專業在讀碩士研究生；主要研究方向為汽車制動系統研究。

TP391+.9;TH6

A

10.16086/j.cnki.issn1000-0380.201601009

修改稿收到日期：2015-03-16。