帶有關節權重的DTW動作識別算法研究

汪成峰， 陳 洪， 張瑞萱， 朱德海， 王 慶， 梅樹立

(1. 中國農業大學信息與電氣工程學院，北京 100083；2. 北京九藝同興科技有限公司，北京 100083)

帶有關節權重的DTW動作識別算法研究

汪成峰1， 陳 洪1， 張瑞萱2， 朱德海1， 王 慶1， 梅樹立1

(1. 中國農業大學信息與電氣工程學院，北京 100083；2. 北京九藝同興科技有限公司，北京 100083)

大多數動作僅包含部分關節的運動，現有方法未對運動劇烈的關節與幾乎不參與運動的關節進行區分，一定程度上降低了動作識別精度。針對這個問題，提出一種自適應關節權重計算方法。結合動態時間規整(DTW)方法，利用獲得的關節權重進行動作識別。首先對分類動作序列進行分段，每段動作序列中運動較劇烈的關節選擇分配更高權重，其余關節平均分配權重；然后提取特征向量，計算兩段動作序列的DTW距離；最后采用K近鄰方法進行動作識別。實驗結果表明，該算法的總體分類識別準確率較高，且對于較相似的動作也能獲得較好的識別結果。關 鍵 詞：動作識別；人體運動分析；動態時間規整；關節權重；姿態特征

人體動作識別是計算機視覺的重要研究領域之一，在視頻監控、人機交互和虛擬現實等方向具有廣泛的應用。在以往的研究中，人們提出了許多人體動作識別的方法，Galna等[1]基于 Vicon動作分析系統和M icrosoft Kinect，提出了一種用于準確的檢測帕金森病癥的動作分析方法。王向東等[2]提出了一種軌跡引導下的舉重視頻關鍵姿態自動提取方法，分析關鍵姿態和杠鈴運動軌跡

的關系，為運動分析提供了技術基礎。總體來說，人體動作識別方法大多選用一個或多個特征參數表示人體動作，并在其特征參數下研究動作比較和分類算法。

人體骨架結構能夠將身體部位簡化表示為具有層次結構的骨骼數據，使用該結構的時間序列數據能夠很直觀地表現人體動作。近年來，隨著若干成本較低且相對精確的動捕系統的普及，例如 M icrosoft Kinect[3]使得實時骨骼數據提取已變得更加容易，基于人體骨架結構的動作識別越來越吸引研究者的關注。Wang等[4]提出了一種結合時間和空間信息的人體結構模型進行動作識別，獲得了較好的效果。張丹等[5]針對基于視覺的體態識別對環境要求較高、抗干擾性差等問題，提出了一種基于人體骨骼預定義的動作識別方法。李學相和安學慶[6]提出一種 Murkowski距離三維圖像動作識別算法，采用非線性優化方法進行求解獲取人體三維行為特征模型，進而實現對人體行為的準確判斷。朱國剛和曹林[7]利用Kinect深度傳感器獲取動作數據，根據坐標系變換構建人體骨骼拓撲結構，通過多類支持向量機訓練以及動作識別。

雖然文獻[4-7]的方法能夠較好地進行動作識別，但這些方法未針對不同關節設置不同權重。對于一些簡單全身動作如跑步，將肢體軀干關節設置相同的權重即可獲得較好的結果；但是對于一些局部關節運動較劇烈的動作，如拳擊或跳躍等，不同關節的運動劇烈程度差異較大，如對所有關節賦予相同權重，將對動作識別的結果造成影響。針對這個問題，本文提出了自適應關節權重的計算方法，并使用動態時間規整方法(dynam ic time warping, DTW)計算兩個動作序列的距離，最后采用K近鄰方法進行動作分類。

1 基于自適應關節權重的特征提取

1.1 基于人體骨架結構的動作序列表示

人體動作序列是人體姿態的時間序列數據，而人體姿態可以由骨架結構近似表示，因此人體動作序列可以采用人體骨架結構中每個關節的時間序列數據表示。關節動作的時間序列數據可以簡單地表示為三維位置的時間序列數據，即三維軌跡。這種動作數據表示方法不具有平移和縮放不變性，對于同一動作，不同體型的數據采集人員會得到不同的結果，而使用關節方向的時間序列數據描述關節運動則可以很好地解決這個問題。因此，本文采用關節方向而非位置對人體骨架姿態進行描述。動作序列可以表示為，其中ip為第i個關節方向的時間序列數據，T為關節數量。本文采用公開動作數據集Florence3D-Action[8]進行實驗，該動作數據集所使用的骨骼模型包含15個關節，如圖1所示。在人體骨架結構中，關節之間存在父子關系，關節的方向由其父關節坐標空間中的相對方向進行描述，根骨(如圖1中的3號關節)采用模型坐標空間中的位置和方向進行描述。

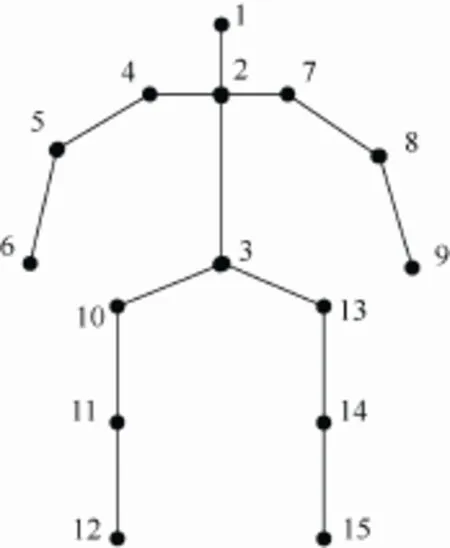
圖1 動作數據集Florence3D-Action使用的骨骼模型，包含15個關節

1.2 動作序列分割

為了計算關節權重，本文首先將動作序列P劃分為N個片段。令為第i個關節的第n個片段的時間序列數據，則，其中為第i個關節的第m幀位置和方向數據，T為關節數量，分別為第n個片段的開始和結束幀。令i p為第i個關節的時間序列數據，則。

一個動作序列通常是由多個原子動作組成，動作序列分割方式會影響動作相似度評價的結果，而動作序列分割為原子動作的方法到目前為止還是一個開放問題。自頂向下的方法通常依賴于專家知識和訓練數據，將動作序列分割為若干原子動作[9-10]；而自底向上的方法通常采用主成分分析與數據壓縮理論分割動作序列[11-12]。這些方法都有各自的局限性，例如需要大量的訓練數據及時間復雜度過高，因此，通常采用 2種方法進行動作序列分割：

(1) 固定片段數量。該方法將不同的動作序列均勻分割為相同數量的片段。對于較短的動作序

列，其分割后的片段也較短；對于較長的動作序列，其分割后的片段也比較長。由于該方法分割不同長度的動作序列都能得到相同數量的片段，因此該方法時序上具有歸一化特性。

(2) 固定時間長度。該方法將不同的動作序列分割為相同長度的片段。對于較短的動作序列，其分割后的片段數量較少；對于較長的動作序列，其分割后的片段數量較多。由于該方法對動作片段提取的特征僅用于關節權重計算，每個動作序列單獨處理，因此不會受到動作片段數量不同的影響。

固定片段數量劃分法的優點是在時序上具有歸一化的特性，但若不同類型的動作長度差異較大，將導致每個片段包含的信息量差異較大，而固定時間長度的劃分方法可以很好地克服這個問題。由于本文使用DTW進行動作序列匹配，該方法實現了兩個不同長度動作序列的歸一化，因此本文選用固定時間長度的動作片段劃分方法。

1.3 關節權重計算

本文按照關節運動劇烈程度，即運動能量大小進行權重分配。令為能量大小相對值，為參考動作序列P的第n個動作片段所有關節能量相對大小的向量。在信息論中，熵用來對信息進行度量，其定義如下

其中，x為隨機變量，f為概率密度函數。對于方差為2σ的高斯分布，熵定義為[13]

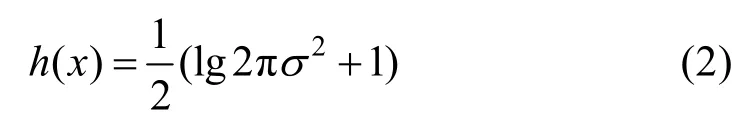
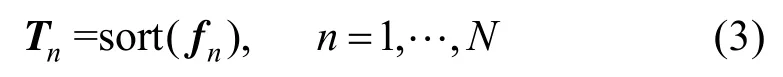
其中，函數sort按照關節的運動能量按降序排列，向量Tn為第n個片段運動能量降序排序的關節ID，。取Tn的前H個關節ID，記為，令，關節權重將根據每個關節 ID在HT中出現的次數進行計算。定義關節i能量最大的片段占所有片段的比例

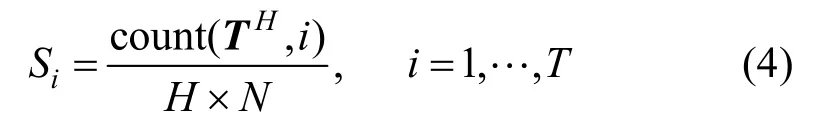
其中，count函數計算HT 中第i個關節出現的次數。圖2為Si的可視化表示，橫坐標為關節的ID，縱坐標為不同動作，每個方格用灰度值表示Si的大小。由圖 2可以看出，不同類型的動作在不同關節的能量分布有較大的差異。

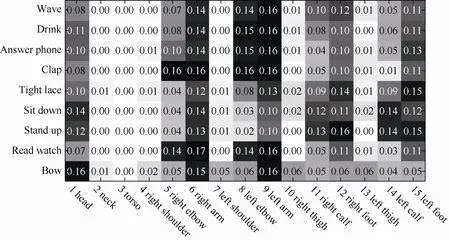
圖2 不同關節的Si可視化表示

當輕微運動及靜止不動時，關節的Si接近0，但在進行動作相似度評價時也需賦予一定的權重。因此本文對運動較劇烈的關節按Si進行權重分配，這些關節占所有權重的比例為α，對其余關節平均分配剩余權重。對Si進行降序排序，得到

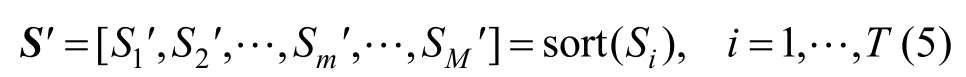
取S′的前m個元素直到這些元素相加大于α，并將其所對應的關節ID加入集合C中，計算得到每

個關節的權重

其中，比例α為運動較劇烈關節所占的總體權重，動作相似度評價結果將受到α取值的影響，具體取值將在實驗章節進行討論。自適應關節權重計算可由以下4個步驟完成：

(1) 將動作序列P劃分為N個片段；

(3) 統計每個關節 ID(i=1,…,T)在向量HT中出現的次數，則可以求得關節i能量較大的片段占所有片段的比例Si；

(4) 取′S中最大的m個元素直到其相加大于α，這些關節的權重為，其余關節按式(6)平分剩余權重。

2 基于關節權重特征的 DTW 動作識別

2.1 經典DTW算法

假設有兩個長度分別為n和m時間序列Q和C，令

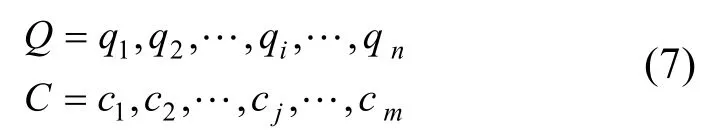
為了對齊兩個時間序列Q和C，需要構造一個大小為n×m的矩陣M，該矩陣的第i行第j列的元素Mi,j為qi和cj的距離 d( qi, cj)，該距離通常使用歐氏距離，即 d( qi, cj) =(qi-cj)2。該路徑為矩陣M中的連續元素，用于表示時間序列Q和C之間的映射關系，定義其中第k個元素為wk=(i, j)k。W可以表示為

DTW方法基于動態規劃的原理求解出最優匹配路徑，該路徑使兩個時間序列Q和C的總匹配距離達到最小

其中，路徑長度 K作為分母用于消除規整路徑長度不同所帶來的影響。

DTW 尋找最優匹配路徑的過程如下：從w1= (1,1)開始，循環計算路徑距離γ(i,j)，基于上述規整的3個條件，到達 wk=(i, j)k的前一個匹配只能為 γ(i - 1, j - 1)、 γ(i- 1,j)和 γ( i,j- 1)其中一個，因此只需要挑選出其中最小的一個，加上當前距離即可得到路徑的最小距離[14]

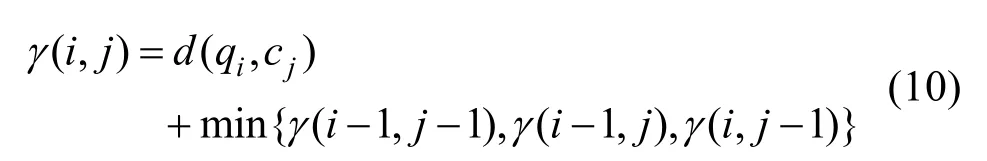
2.2 人體動作識別

動作序列P由若干幀骨架數據組成，本文逐幀對骨架特征進行提取，并基于該特征進行動作識別。動作序列的每一幀可以看作靜態人體骨架結構數據，其包含了每個關節的位置和方向數據。由于采用關節的方向數據描述人體骨架結構具有平移和縮放不變性，因此本文在預處理階段通過關節位置數據計算出關節方向數據，再采用關節方向數據即關節的級聯四元數對人體骨架結構進行描述。

文獻[15]定義了兩個四元數距離的度量方式，本文將此用于對靜態骨架結構進行相似性度量。設參考向量 E0∈R3，q1、q2為兩個單位四元數，如圖3所示，將E1旋轉到E2，若= [x, y, z, w] =[n ·sinφ, cosφ]，則q1、q2的距離可以定義為

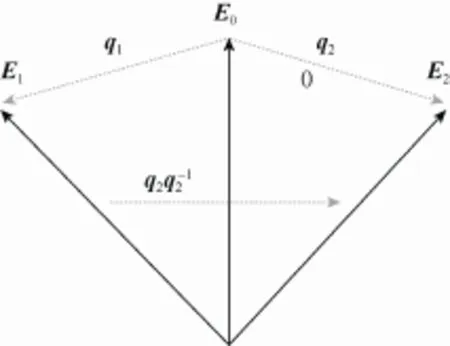
圖3 四元數距離計算

輸入動作序列為 P= [ p1, p2,…,pr,…, pR]和Q = [q1, q2,…,qr′,…,qR′]，其中R和R′分別為P和

計算DTW的代價矩陣，通過式(10)得到最優規整路徑 W= w1, w2,…,wk,… ,wK，其中K為路徑W的長度，wk為采用式(12)計算的每對匹配幀的距離，最后得到規整路徑距離的平均值

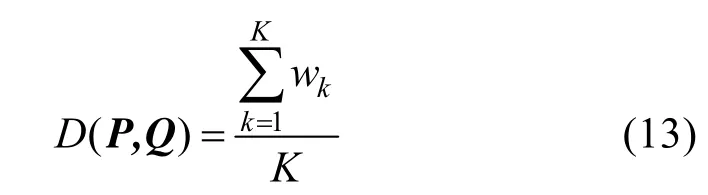
即動作序列P和Q的距離度量結果。圖 4為Florence3D-Action動作數據集中兩個“Sit down”動作采用動態規整路徑進行幀匹配的示意圖。

圖4 兩個動作序列的幀匹配示意圖

基于式(13)的距離度量函數，本文采用K近鄰分類器對未知動作序列的類型進行分類。設L={λ1,λ2,… ,λl}為l個訓練樣本標記，訓練動作數據集 C={(Pi,λi)|1 ≤i≤ N}包含N個動作序列，λi∈ L為動作序列Pi所屬的類別。輸入待分類動作序列Q，采用式(13)計算Pi與Q的距離

將訓練樣本按照Di進行升序排序，前K個訓練樣本構成近鄰樣本集。統計訓練樣本中第j個(1≤j≤l)標記的樣本個數，采用多數表決原則決定未知動作序列Q的所屬類別λ

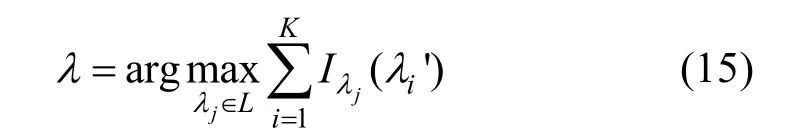
其中，函數I為指示函數，定義為

算法總體流程如圖5所示。

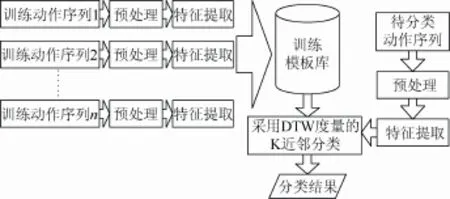
圖5 算法總體流程

3 實驗結果與分析

實驗采用真實世界中采集的動作數據集測試本文方法的性能。實驗環境為CPU：Intel i7-4790K，內存：8 G，操作系統：Windows 8，集成開發環境：Matlab 2012。

3.1 實驗數據

采用公開的動作數據集Florence3D-Action對本文方法的有效性進行驗證。采用微軟 Kinect對人體動作數據以每秒15幀進行采集，其人體骨架包含15個關節位置。該數據集包含9類動作，每類動作由10人重復2～3次完成，共獲得215個動作序列。該數據集中包含一些較為相似但類型不同的動作，例如“Drink from a bottle”與“Answer phone”這兩個動作不屬于同類動作，但是較為相似，僅在手部的高度有些差異，如圖6所示。

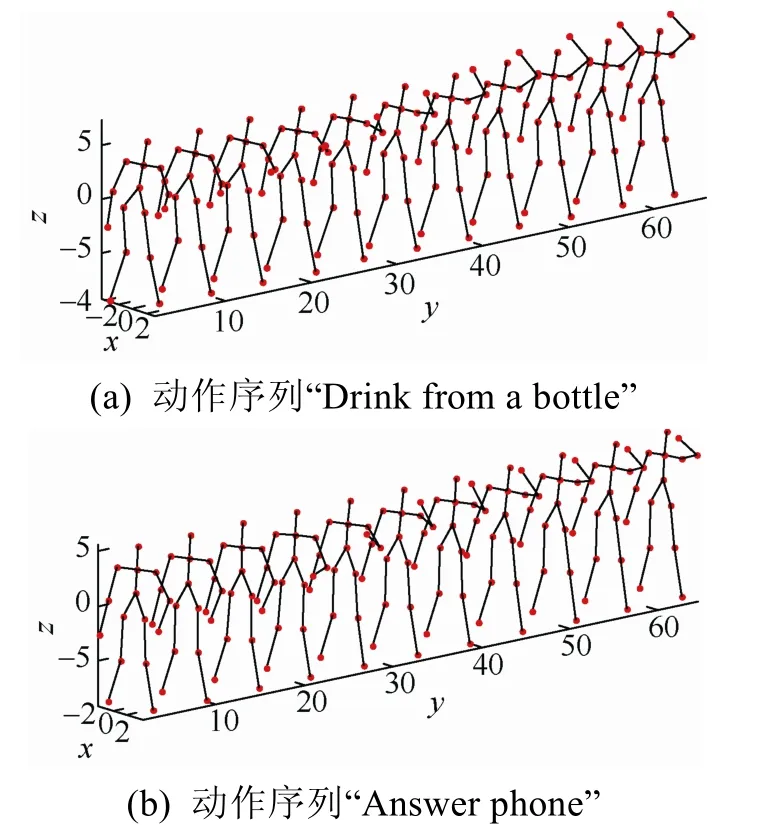
圖6 “Drink from a bottle”與“Answer phone”動作比較

3.2 實驗結果

本文在動作數據集Florence3D-Action采樣交叉驗證的策略進行實驗，即一半的數據用于訓練分類器，另一半數據用于驗證分類準確度。定義測試數據集中每個類型動作的分類準確率為

其中，x為動作類型， correct( x)為測試數據集中屬于x的動作序列被正確分類的次數，total(x)為測試數據集中屬于x的動作序列的總數。圖7顯示了該動作數據集中五類動作在不同參數下的分類準確率，其中，參數H分別取5、6和7，參數α分別取0.6、0.7、0.8和0.9。

圖7 采用自適應關節權重的分類結果

從圖7可以看出，選擇較小的H和α能夠提高相似動作的識別率，但是太小的H或α容易造成差異較大的動作識別率下降；選擇較大的H和α則降低了權重選擇方法的效果，相似的動作識別率出現明顯的下降，總體來說H=6，α=0.7時分類準確率較高。此外，在不同的H和α的條件下，動作分段長度在0.8附近具有較高的識別率。

圖8為動作分段長度在0.8的條件下，取不同H和α得到的動作識別率。可以看出，H=6，α= 0.7時能夠得到最優的分類準確率。結合圖 7的結果，得到本文方法的最優參數，即動作分段長度取0.8，H=6和α=0.7。

將動作數據集Florence3D-Action采用4種隨機的訓練集和測試集劃分方式，在選取本文算法參數H=6，α=0.7，分割時間片段為0.8 s條件下，表 1給出了本文方法與其他方法實驗結果比較，結果顯示本文方法有較好地識別結果。本文方法的平均混淆矩陣如圖 9所示，可以看出，本文方法對動作具有較高的識別率。

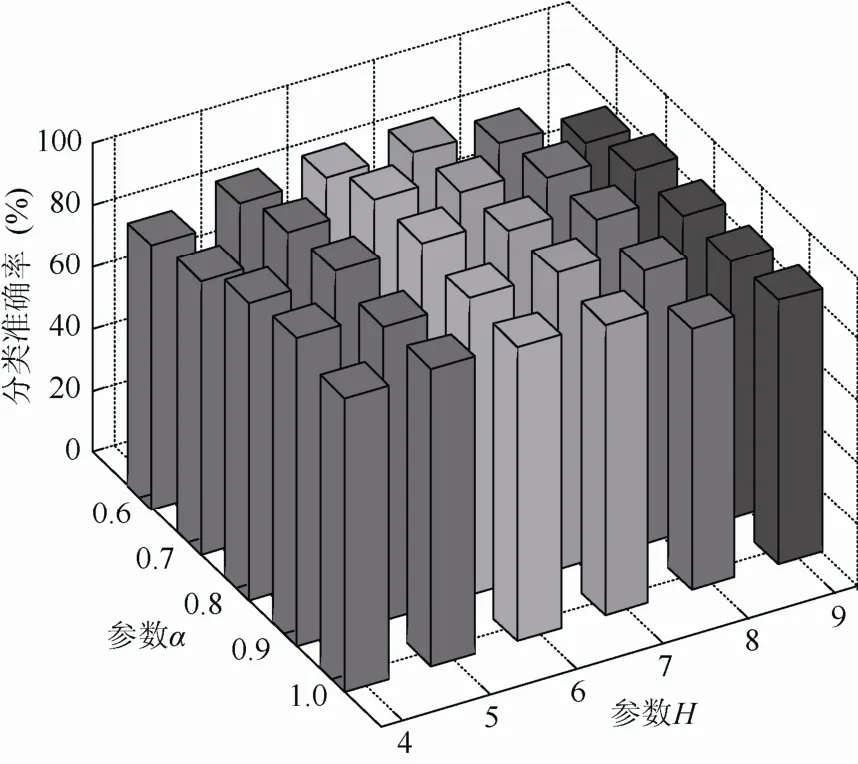
圖8 選取不同H和α得到的分類結果

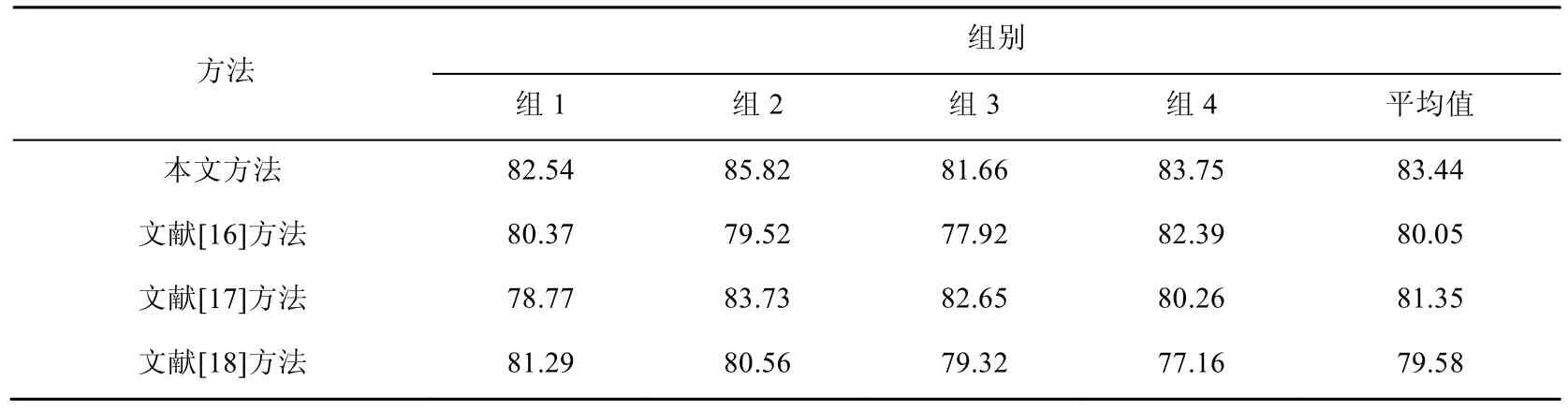
表1 Florence3D-Action動作數據集上分類準確率對比(%)

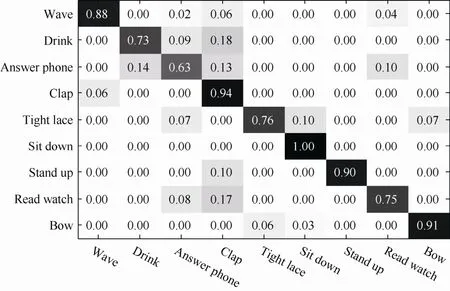
圖9 本文方法在選擇最優參數下在Florence3D-Action進行實驗獲得的混淆矩陣

4 結 束 語

本文提出了一種自適應關節權重計算方法，該方法從運動特性出發，將動作序列劃分為多個子片段，通過每個子片段不同關節的熵值計算關節權重，再將關節權重與DTW結合計算兩個動作序列的距離，最后采用K近鄰方法進行動作識別。本文方法充分利用了不同關節的運動特性，對運

動較為劇烈的關節與幾乎靜止不動的關節在權重上進行區分。實驗結果表明，該算法具有較高的識別準確率，對相似動作也能有較好的區分。在后續研究中，將考慮基于本文的自適應關節權重，進一步研究動作特征及分類策略，以提高識別準確率。

[1] Galna B, Barry G, Jackson D, et al. Accuracy of the M icrosoft Kinect sensor for measuring movement in people w ith Parkinson’s disease [J]. Gait & Posture, 2014, 39(4): 1062-1068.

[2] 王向東, 張靜文, 毋立芳, 等. 一種運動軌跡引導下的舉重視頻關鍵姿態提取方法[J]. 圖學學報, 2014, 35(2): 256-261.

[3] Zhang Z Y. M icrosoft Kinect sensor and its effect [J]. IEEE MultiMedia, 2012, 19(2): 4-10.

[4] Wang C Y, Wang Y Z, Yuille A L. An approach to pose-based action recognition [C]//CVPR 2013: 26th Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. New York: IEEE Press, 2013: 915-922.

[5] 張 丹, 陳興文, 趙姝穎, 等. 基于 Kinect 骨骼預定義的體態識別算法[J]. 計算機應用, 2014, 34(12): 3441-3445.

[6] 李學相, 安學慶. 基于三維圖像動作識別算法研究[J].計算機仿真, 2013, 30(9): 374-377.

[7] 朱國剛, 曹 林. 基于 Kinect傳感器骨骼信息的人體動作識別[J]. 計算機仿真, 2014, 31(12): 329-333.

[8] Seidenari L, Varano V, Berretti S, et al. Recognizing actions from depth cameras as weakly aligned multi-part bag-of-poses [C]//Computer Vision and Pattern Recognition Workshops (CVPRW), IEEE Conference on. New York: IEEE Press, 2013: 479-485.

[9] Beaudoin P, Coros S, van de Panne M, et al. Motion-motif graphs [C]//ACM Siggraph/Eurographics Symposium on Computer Animation (2008). New York: ACM Press, 2008: 117-126.

[10] Müller M, Baak A, Seidel H P. Efficient and robust annotation of motion capture data [C]//ACM Siggraph/ Eurographics Symposium on Computer Animation (2009). New York: ACM Press, 2009: 17-26.

[11] Barbi? J, Safonova A, Pan J Y, et al. Segmenting motion capture data into distinct behaviors [J]. Proceedings of Graphics Interface 2004. Canadian Human-Computer Communications Society, 2004, (5): 185-194.

[12] López-Méndez A, Gall J, Casas J R, et al. Metric learning from poses for temporal clustering of human motion [CD]. Proceedings BMVC 2012 Pages: CD-rom, 2012: CD-rom.

[13] Shannon C E, Weaver W. A mathematical theory of communication, 1949 [M]. Urbana: University of Illinois Press, 1949: 24-30.

[14] Berndt D J, Clifford J. Using dynamic time warping to find patterns in time series [C]//Working Notes of the Know ledge Discovery in Databases Workshop, United States, Massachusetts: Association for the Advancement of A rtificial Intelligence Press, 1994: 359-370.

[15] 沈軍行, 孫守遷, 潘云鶴. 從運動捕獲數據中提取關鍵幀[J]. 計算機輔助設計與圖形學學報, 2004, 16(5): 719-723.

[16] Ohn-Bar E, Trivedi M M. Joint angles sim ilarities and HOG2for action recognition [C]//Computer Vision and Pattern Recognition Workshops (CVPRW), 2013 IEEE Computer Society Conference on, New York: IEEE Press, 2013: 465-470.

[17] Xia L, Chen C C, Aggarwal J K. View invariant human action recognition using histograms of 3D joints [C]// Computer Vision and Pattern Recognition Workshops (CVPRW), 2012 IEEE Computer Society Conference on, New York: IEEE Press, 2012: 20-27.

[18] 應 銳, 蔡 瑾, 馮 輝, 等. 基于運動塊及關鍵幀的人體動作識別[J]. 復旦學報: 自然科學版, 2014, (6): 815-822.

Research on DTW Action Recognition A lgorithm w ith Joint Weighting

Wang Chengfeng1, Chen Hong1, Zhang Ruixuan2, Zhu Dehai1, Wang Qing1, Mei Shuli1

(1. College of Information and Electrical Engineering, China Agricultural University, Beijing 100083, China; 2. Beijing Jiu Yi Tong Xing Technology Co., Ltd, Beijing 100083, China)

Human motions always contain only motions of some body parts, but much of the existing methods on action recognition don’t take the motion intensity of each joint into account, which lower the accuracy of action recognition in some extent. To solve this problem, an adaptive joint weighting scheme is proposed to calculate the weight of each joint and combined the weights w ith dynam ic time warping (DTW) to recognize actions. Firstly, the action sequence was segmented into several segments and some most violent joints in each segment are assigned higher weight while the remaining joints are evenly weighted. Then feature vectors of two action sequences were extracted and the distance between two action sequences were calculated by DTW. Finally the action recognition was achieved by K-nearest neighbor method. The experiments showed that the overall classification accuracy of the proposed method is higher, and the result is also good for some similar actions.

action recognition; human motion analysis; dynam ic time warping; joint weight; pose feature

TP 301.6

10.11996/JG.j.2095-302X.2016040537

A

2095-302X(2016)04-0537-08

2016-03-08；定稿日期：2016-05-04

國家科技支撐計劃項目(2013BAH48F02)

汪成峰(1988–)，男，福建南平人，博士研究生。主要研究方向為虛擬現實與人機交互技術。E-mail：147750373@qq.com

陳 洪(1976–)，男，四川大竹人，副教授，博士。主要研究方向為虛擬現實與人機交互技術、數字游戲與虛擬學習環境。

E-mail：norman_chen@263.net