基于M-V法、Wahl法和有限元法的汽輪機隔板的強度對比分析

楊光輝， 陳慶波

(北京科技大學機械工程學院，北京 100083)

基于M-V法、Wahl法和有限元法的汽輪機隔板的強度對比分析

楊光輝， 陳慶波

(北京科技大學機械工程學院，北京 100083)

長期處于高溫高壓的汽輪機隔板只有在一定強度和剛度下，才能安全進行生產工作。分別基于經典算法Wahl法、M-V法和有限元法，對某亞臨界狀態機組隔板進行強度分析和對比。結果表明，隔板最大應力在靠近中分面葉片的進氣葉根處，最大應變在中分面內徑內環處，板體最大應力在垂直于中分面的內環內徑處，其中有限元法和 Wahl法誤差較小，驗證了有限元方法的可行性。

汽輪機隔板；有限元；Wahl法；強度分析

隔板用于固定靜葉片和防止汽輪機各個級間漏氣，所以在汽輪機中起著至關重要的作用。隨著大容量、高參數的汽輪機組被廣泛地使用，高壓缸中的隔板處于非常惡劣的環境下，不僅有高溫還有很高的壓力差，使隔板會產生一定的撓度。隔板撓度最大的地方在中分面靠近內徑處，如果隔板沒有足夠的強度和剛度，那么由正常工作產生的撓度會大于動靜葉之間的間隙，這樣動靜隔板相碰便會發生非常大的事故。因此，合理正確地分析隔板的應力和撓度對汽輪機隔板的安全工作起著重要的作用。基于大型有限元軟件ANSYS Workbench 15.0對隔板進行有限元分析，并將其與經典算法——Wahl法和M-V法進行了比較，驗證了有限元法對高壓隔板計算的可行性。

1 M-V法

M-V法又稱 Sm ith法，是最早采用的隔板計算方法，首先被英國M-V透平制造廠用于計算隔板強度。其對于隔板計算作了如下假定[1]：

(1) 隔板外緣固定在完全剛性的支座上；

(2) 隔板上承受均勻分布的蒸汽載荷；

(3) 支反力沿支承周邊分布依照正弦曲線規律(與實際情況不符)；

(4) 在計算隔板本身的應力和撓度時，假定靜葉絕對剛性；在計算靜葉應力和撓度時，假設隔板外緣和板體是絕對剛性的；

(5) 隔板受力后隔板的徑向截面形狀保持不變；

(6) 不考慮隔板本身的曲率，即計算時對于力和變形的關系利用直梁公式。

隔板體最大應力，在垂直于隔板中分面的內徑處，其值為

隔板體最大撓度，在隔板中分面內徑處，其值為

式中，Δp為隔板兩側最大壓差；D為氣缸內徑；S為隔板體厚度；J為隔板的計算慣性矩；E為工作溫度下隔板材料的彈性模量；Kσ為應力計算系數；KD為撓度計算系數。

該方法還可以計算靜葉中的最大應力和最大撓度(此時假定隔板體為絕對剛性)，其公式如下：

靜葉片的最大撓度為

靜葉片最大應力為

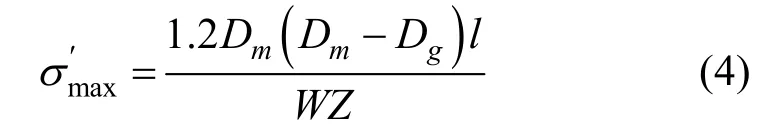
式中，Dm為靜葉平均直徑(m)；Dg為汽封處內徑；l為靜葉高度(m)；Z為靜葉數；E為靜葉材料工作溫度時彈性模量(MPa)；I為靜葉橫截面對X-X軸的慣性矩(m4)；W為靜葉截面對X-X軸的截面系數(m3)，W=I/e，其中e為離中性軸X-X最邊緣的距離。

則在靠近隔板中分面汽封內徑處的最大撓度的計算公式由fmax和兩部分組成

已知Δp=0.92 MPa，D=1.708 m，Dm=1.369 m，Dg=0.750 m ， l=0.170 m ， S=0.119 m ，J=5.673368×10–5m4，由以上公式可以求得

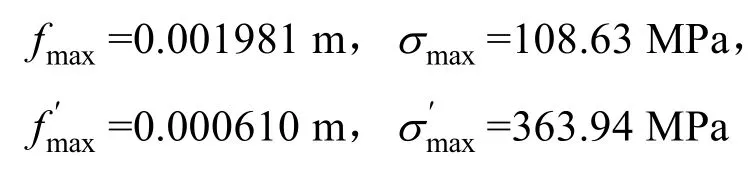
隔板體最大撓度為

隔板體最大應力為σmax=108.63 MPa。

2 Wahl法

與M-V法相比，Wahl法基于更加嚴格的理論前提。其不考慮靜葉的存在，把隔板當作一整塊半圓環，利用曲梁斜彎曲理論的近似解法，得到隔板的受力狀態。由于高壓級隔板的靜葉往往比較短，因此Wahl法對計算靜葉較短的高壓隔板的計算與實際情況比較吻合，但是其缺點就是無法計算葉片的最大應力。Wahl提出在隔板的內、外徑差別不是特別大時，即 d/ D0≥ 0.4，隔板在受力后其徑向截面不發生變形[2]。

在中心截面r=r0處，隔板的撓度最大，此處的最大撓度為

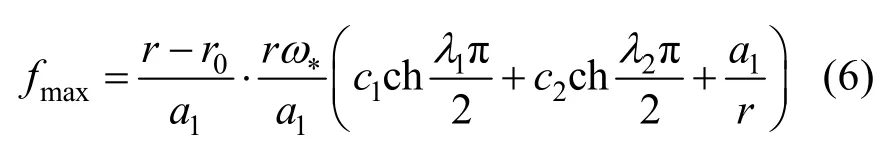
式中，c1、c2、λ1、λ2為待求系數；r0為氣缸內環的內半徑；r=r0+a； a=(R -r0)/2；R為外環的外半徑；；a1=2e-a； e=(r1-r0)/2；r1=r+a；Jx為截面對O1x軸的慣性矩；E為彈性模量；；C為隔板的扭轉剛度； B =2eΔ p( r+ e) + q0r0；；

其中：Δp為壓差；q0和m0為汽封處轉化而來的均布載荷和均布力矩。

最大彎應力發生在隔板內環垂直于中分面的靠近內徑的位置

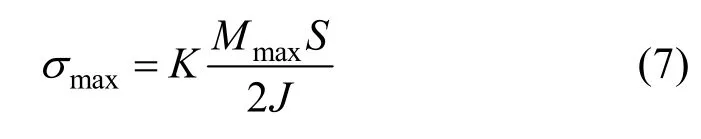
式中

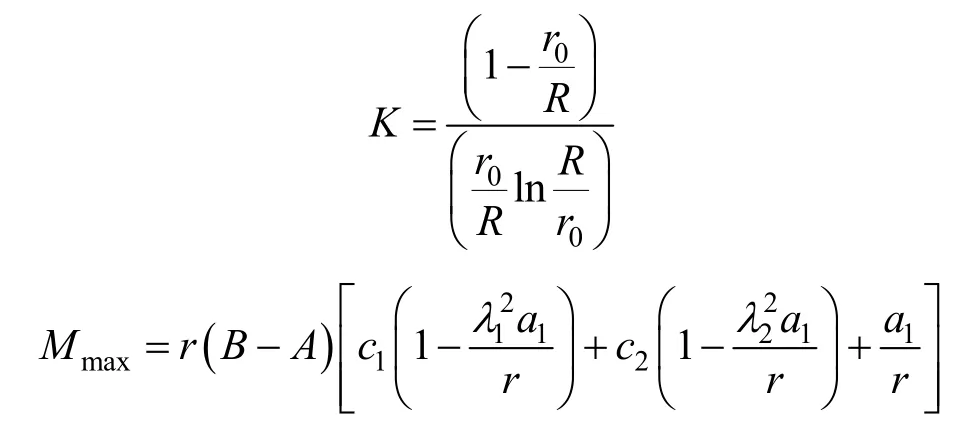
其中，S為隔板的厚度；K為應力沿徑向截面分布不均勻的系數；J為截面對O1x軸的慣性矩。

由以上公式可以求得：

隔板體最大撓度為Δ=1.21 mm；

隔板體最大應力為σmax=14.8 MPa。

3 有限元法

3.1 模型的建立

某汽輪機廠的亞臨界狀態氣缸，機組的額定蒸汽壓力為16.67 MPa，主蒸汽溫度為538 ℃，隔板的參數設為：外環外徑為1 838 mm，外環內徑為1 518 mm，內環外徑為1 220 mm，內環內徑為795 mm，靜葉高度為 170 mm，靜葉最大寬度為32 mm，靜葉數量為46片。

在ANSYS Workbench 15.0建立了一個靜力學分析項目，將 SolidWorks建立的模型導入到DM(DesignModeler)模塊中，定義材料的屬性如下：①靜葉葉片及焊接塊：彈性模量為1.607×105MPa，泊松比為 0.3；②隔板內外圈：彈性模量為1.696×105MPa，泊松比為0.3。如圖1所示，對模型進行網格劃分，內外環以及焊接塊由于形狀比較簡單，采用掃略的方式，靜葉部分采用四面體單元進行劃分，節點數為423 638，單元數為127 499。

圖1 隔板網格劃分模型

3.2 位移邊界條件設定

圖2為隔板的邊界條件示意圖，圖中向右為x正方向，向上為y正方向，垂直xy平面向外方向為z正方向。由于隔板的外緣支承在氣缸或隔板套的隔板槽中，所以軸向約束 uz=0；隔板外環由緊固螺栓聯接固定在氣缸或隔板套上，上下兩半對稱，則對稱約束uy=0，不轉動所以Ry=0；隔板頂部有定位鍵，防止隔板在蒸汽壓力下移動旋轉，所以外環環面ux=0[3]。

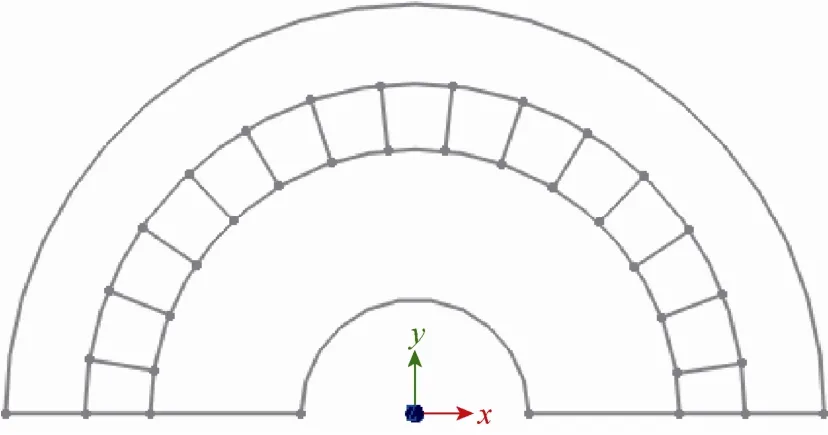
圖2 隔板邊界條件示意圖

3.3 力的邊界條件設定

汽輪機受力情況比較復雜，這是因汽輪機的工作原理所致，即隔板內環和外環受到前后壓力差的作用。蒸汽通過噴嘴葉柵，蒸汽流速增大、流速方向改變，同時蒸汽對隔板靜葉必然產生一定的反作用力。如圖 3所示，由動量定理可知，單個靜葉流道內蒸汽受到軸向、周向作用力分別為[4]

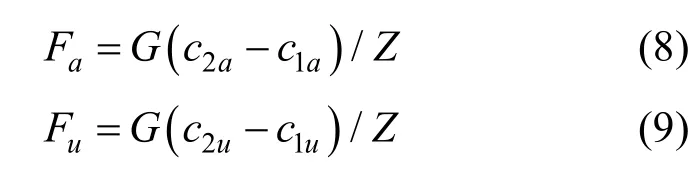
式中，c1為進氣速度；c1a、c1u分別為c1的軸向、周向分量；c2為出氣速度；c2a、c2u分別為c2的軸向、周向分量；Z為隔板葉片數；G為蒸汽流量。

在Ansys Workbench 15.0中采用Fluid Flow (CFX)進行流體分析，建立兩個靜葉噴嘴的流體模型，采用的是掃掠方式劃分網格，其中共計68 000個節點，60 909個單元。圖3所示模型的左右為葉片的內弧和背弧壁，上下為隔板內外環壁，前面為進氣側，后邊為出氣側。

模型設定為穩態計算，求解方程為Navier-Stokrs方程，湍流模型選擇k-ε模型。流體的進口條件設定為蒸汽流量10.63 kg/s，出口邊界條件設定為蒸汽壓力15.76 MPa，壁面為絕熱無滑移條件[4]。

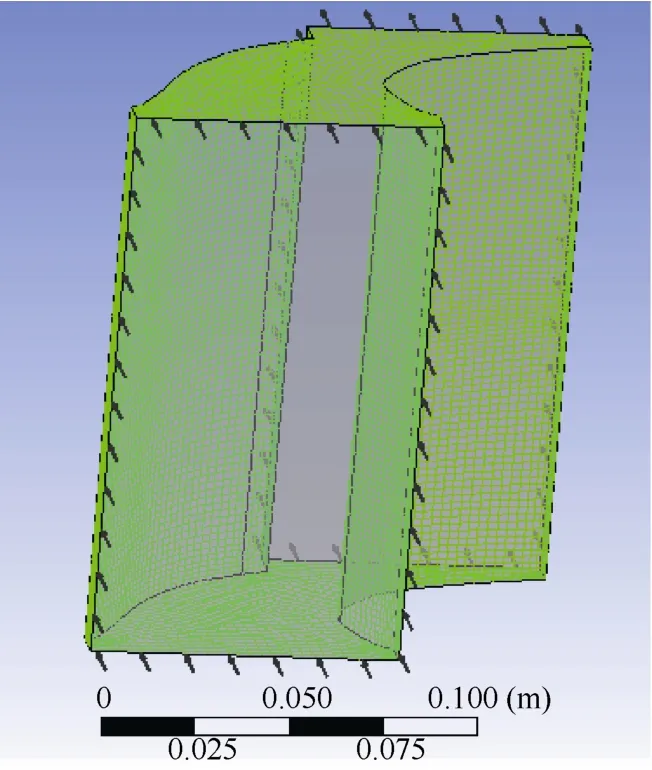
圖3 靜葉單通道計算模型

圖 4所示為計算得到的流場壓力分布云圖，可以看出從進氣側到出氣側，隨著靜葉葉片弦長的增加蒸汽壓力在不斷的減小，在流場最后出口附近出現負壓。進口壓力約為16.64 MPa，出口壓力約為15.72 MPa，進出口的蒸汽壓差為0.92 MPa。

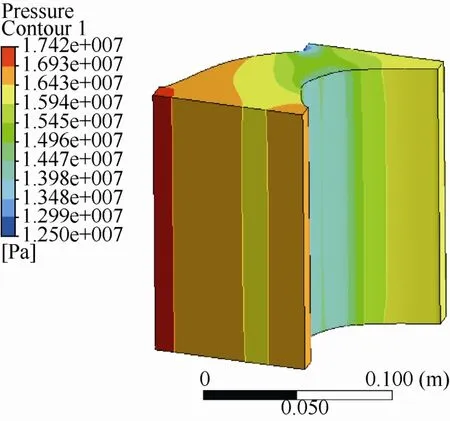
圖4 流場壓力分布云圖

圖 5所示為計算得到的流場速度矢量分布云圖，可以看出進口速度的軸向分量差不多為零，只有軸向速度分量，隨著靜葉葉片弦長的增加，蒸汽的速度也在不斷地增加。

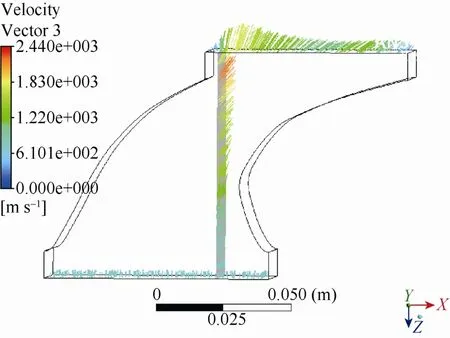
圖5 流場速度矢量圖

由表1以及式(8)、(9)可以算出整個隔板的受力情況，其中隔板體內環和外環受到前后壓差的壓力，靜葉片受到蒸汽氣流的反作用力，具體數值見表2。

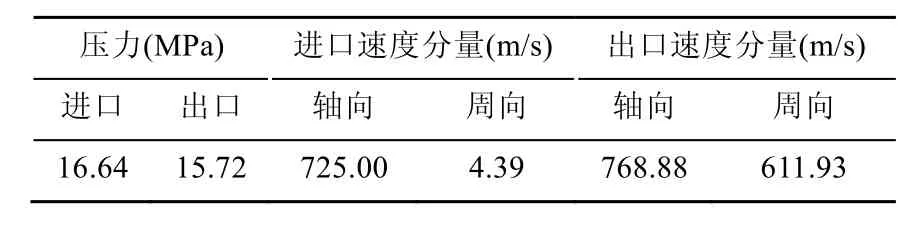
表1 流體計算結果

表2 隔板受力值

3.4 有限元法計算結果分析

由隔板應變云圖(圖6)可以看出，隔板中靠近中心截面葉片的葉根處受到的應力最大，且在進氣一側達到531.3 MPa，然而板體中應變最大的位置出現在與中心截面垂直的內環內徑處(圖7)；從隔板的應變云圖(圖8)可以看出，隔板的變形從外環到內環逐漸增大，最大撓度出現在中心截面的內環內徑處，達到了1.07 mm。這一結果與Wahl法將隔板簡化為懸臂梁的思想一致，隔板外環相當于懸臂梁的根部，承受著整個隔板的應力[5-8]。

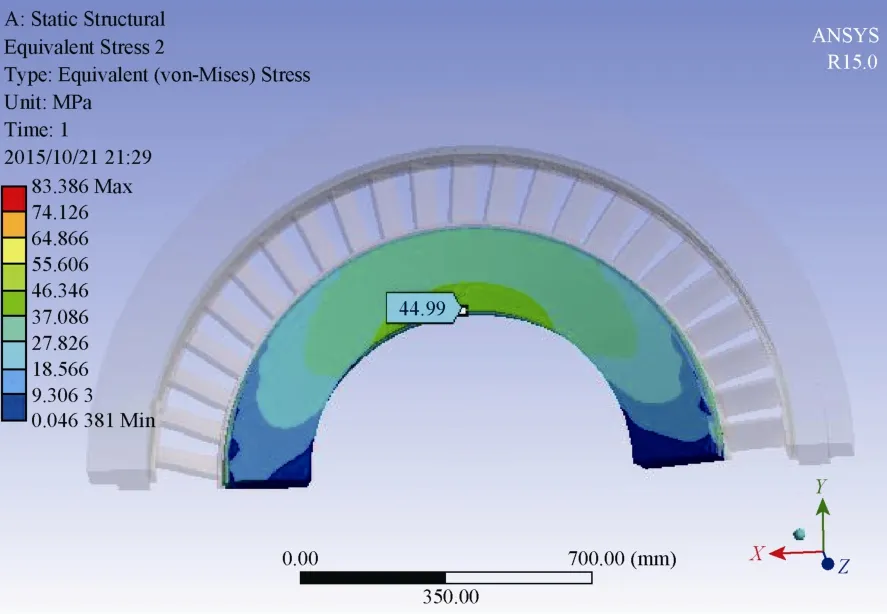
圖7 隔板板體應力云圖

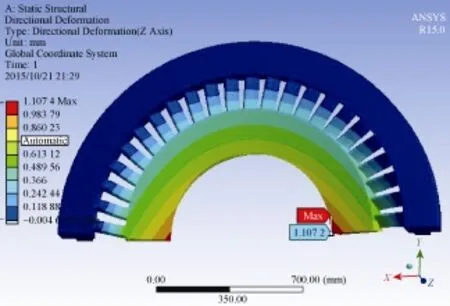
圖8 隔板整體應變云圖

隔板的撓度大小對隔板的設計起著至關重要的作用，因為變形過大會使動靜隔板發生摩擦、碰撞等事故，如果有靜葉折斷，那么斷葉會隨著蒸汽進入下一級隔板，從而造成整個汽輪機癱瘓的事故發生。由有限元云圖顯示可知，隔板體的最大應力和撓度位置與Wahl法計算最大應力撓度的位置大致符合，且有限元法進一步考慮了隔板的結構、受力以及位移約束，所以認為其結果更加接近真實性。表3為隔板撓度以及應力的3種計算結果的對比，表中數據顯示，Wahl法相比M-V法具有更小的誤差，表明Wahl可以在高壓級隔板初級設計中采用。而M-V法最大撓度與有限元法相差太大，是因為M-V法適合靜葉較長的隔板，隔板的最大撓度是板體撓度與靜葉撓度相加[9]。

表3 有限元法與Wahl法、M-V法比較

4 結 論

M-V法最大撓度與有限元法相差太大，是因為M-V法適合靜葉較長的隔板，隔板的最大撓度是板體撓度與靜葉撓度相加。有限元法與Wahl法的隔板撓度相差不大，而且隔板體的最大應力和撓度位置與Wahl法計算最大應力撓度的位置大致符合，隔板最大應力位置在靠近中分面的葉片的葉根處，最大撓度在中分面內徑處。

[1] 丁有宇. 汽輪機強度計算手冊[M]. 北京: 中國電力出版社, 2010: 73-113.

[2] 吳厚鈺. 透平零件結構和強度計算[M]. 北京: 機械工業出版社, 1982: 253-263.

[3] 周軼喆, 劉明軍, 胡柳欣, 等. 汽輪機隔板的塑性變形分析[J]. 動力工程, 2009, 29(1): 46-48, 67.

[4] 董成龍. 大型汽輪機的隔板剛度特性研究[D]. 大連:大連理工大學, 2013.

[5] 劉 平. 典型隔板的強度剛度有限元分析[J]. 汽輪機技術, 2004, 46(5): 333-335.

[6] 馬 駿, 趙海峰, 孫 偉, 等. 汽輪機隔板強度計算方法的比較[J]. 東方電氣評論, 2015, 29(114): 29-32.

[7] Chen J P, Yang G H, Yang B. Finite element analysis of steam turbine diaphragm [J]. Computer Aided Drafting, Design and Manufacturing, 2014, 24(4): 60-63.

[8] Chen J P, Zhao W D, Cai W H, et al. Strength analysis of steam turbine diaphragm w ith a crack [J]. Computer Aided Drafting, Design and Manufacturing, 2015, 25(1): 52-55.

[9] 胡柳欣, 忻建華, 葛 誦, 等. 汽輪機隔板高溫蠕變壽命評估方法的研究[J]. 動力工程, 2009, 29(3): 232-235.

Com parison Analysis of Intensity for the Turbine Diaphragm Based on Wahl, M-V and Finite Element Methods

Yang Guanghui, Chen Qingbo

(School of Mechanical Engineering, University of Science and Technology Beijing, Beijing 100083, China)

Steam turbine can remain a safe production state for a long period under the environment of high temperature and high pressure if it has certain good strength and intensity. The methods of Wahl, M-V and finite element analysis were used in analysis of intensity for a subcritical state turbine diaphragm. The results showed that the maximum stress of the diaphragm appeared at the blade’s enter side of the blade root, the maximum strain appeared at the equatorial plane at an inner diameter of the inner ring, and the maximum stress of the board appeared at the inner diameter of the inner ring which was vertical to the equatorial plane. The errors of finite element method and Wahl method were smaller, so it proved the reliability of finite elements analysis.

turbine diaphragm; finite elements analysis; Wahl method; intensity analysis

TK 263.2

10.11996/JG.j.2095-302X.2016040577

A

2095-302X(2016)04-0577-05

2015-11-01；定稿日期：2016-01-09

北京高等學校青年英才計劃項目(YETP0369)；中央高校基本科研業務費項目(FRF-BR-15-047A)

楊光輝(1977–)，男，山東諸城人，副教授，博士。主要研究方向為機械裝備行為及控制等。E-mail：yanggh@ustb.edu.cn