組合同倫法求一般非線性規劃問題

黃青群

（河池學院數學與統計學院，廣西 宜州 546300）

組合同倫法求一般非線性規劃問題

黃青群

（河池學院數學與統計學院，廣西 宜州 546300）

文章把含有等式約束和不等式約束的一般非線性規劃問題轉化為只有不等式約束的非線性規劃問題，然后構造一個新的同倫方程，與牛頓法結合得到一個新的同倫算法，在變形錐條件下，證明了算法的全局線性收斂性。

組合同倫；一般凸規劃；全局收斂性；牛頓法

1 引言

同倫算法是大范圍的收斂算法，它是求解非線性方程組的一種新途徑。由于非線性方程組的復雜性，導致很難直接求得其相應的解，此時可以構造一個相對容易求解的方程組，從求解后者的解出發，通過路徑跟蹤從而求得前者的解。這就是同倫算法的基本思路。同倫算法已經應用到了不同的非線性規劃問題，如線性互補問題[1]、多目標優化問題[2]、均衡規劃問題[3]等等。本文把含有等式約束和不等式約束的一般非線性規劃問題轉化為只有不等式約束的非線性規劃問題，然后構造一個新的同倫方程，與牛頓法結合得到一個新的同倫算法，在變形錐條件下，證明了算法的全局線性收斂性。

考慮一般非線性規劃問題(GNLP)：

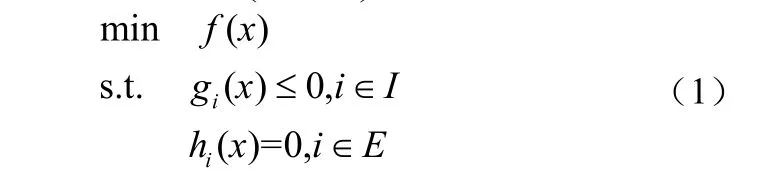
充分光滑的凸函數。由文獻[4]知可將問題(1)轉化為問題(2)進行求解：

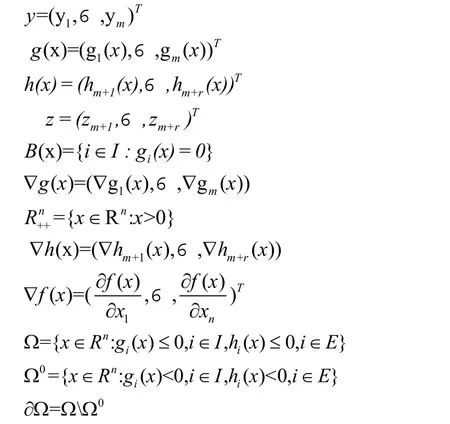
問題(2)的KKT系統為：

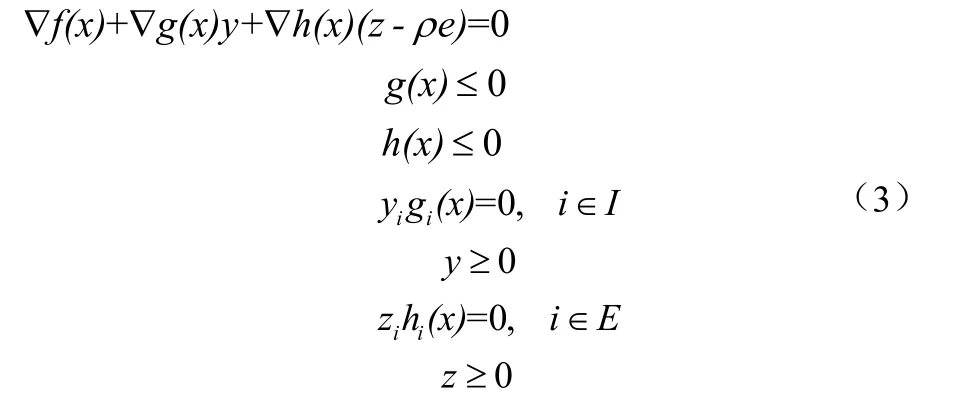
目前為止，很多文獻在“法錐條件”、“弱法錐條件”、“擬法錐條件”或“偽法錐條件”下證明了同倫路徑的存在性以及收斂性。本文在變形錐條件下證明同倫路徑的存在性以及收斂性，該條件比“法錐條件”、“弱法錐條件”、“擬法錐條件”及“偽法錐條件”更容易滿足。……