體外預應力簡支梁抗彎極限承載力研究

李英田（嘉應學院地理科學與旅游學院，廣東 梅州514015）

體外預應力簡支梁抗彎極限承載力研究

李英田（嘉應學院地理科學與旅游學院，廣東 梅州514015）

推導了單轉向塊折線形體外預應力簡支梁的極限承載力公式，進行了1根與理論模型一致的簡支T梁試驗，試驗中，對T梁的受力過程、破壞形態、承載力和變形情況進行全程記錄（采用自動采集系統TDS530采集）和分析。理論計算與試驗結果對比表明，理論計算公式偏于保守。另外，與普通鋼筋混凝土簡支梁相比，施加了體外預應力后，梁的剛度有顯著提高。

簡支梁；體外預應力；極限荷載

引言

體外預應力結構從20世紀30年代發展至今，其結構體系一直在不斷的創新與改進。體外預應力技術具有施工簡便、提高結構承載能力等優點，它是后張預應力體系的重要分支之一。體外預應力受力過程中力筋與混凝土在梁的絕大部分無接觸（端頭和轉向塊處接觸）。隨著預應力筋的各種防腐措施漸趨完善，力筋的防腐已不十分困難，結構的耐久性得到保證，體外預應力混凝土結構得到了較大規模的發展。但對于體外預應力簡支梁的極限承載力問題，國內外學者雖作了一定量的理論和試驗研究，不過得出的結果往往具有一定的離散性和局限性。

本文推導了單轉向塊折線形體外預應力混凝土簡支梁的抗彎極限承載力公式，進行了一根3m長體外預應力T型簡支梁的試驗，并把理論值與試驗值做了對比。

1 公式推導

1.1 混凝土應力-應變關系

混凝土應力-應變本構關系：拋物線上升段+水平直線段形式（如圖1所示）。

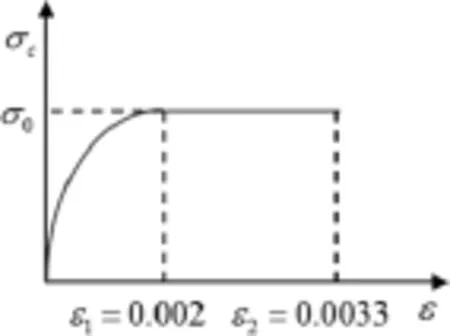
圖1 混凝土應力-應變曲線圖

式中：

fca——棱柱體抗壓極限強度；

ε1——取0.002；

ε2——取0.0033。

1.2 體外預應力筋應力-應變關系

體外預應力筋的應力-應變關系如圖2所示。

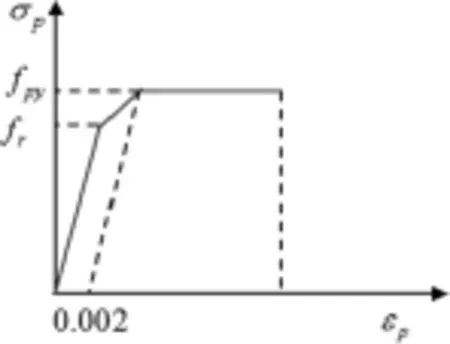
圖2 預應力筋應力-應變曲線圖

式中：

σ、△σ——應力、應力增量；

L、△L——力筋計算長度、力筋伸長量；

E——體外預應力筋彈性模量；

fpy、fr——以0.2%的殘余應變所對應的力筋屈服強度、0.9fpy。

1.3 計算基本假定

（1）不計重力對力筋線型影響（即在錨固點和轉向塊之間，索段為直線）。

（2）彈性階段，變形均符合平面應變平截面假定，忽略主梁的軸向變形。

（3）梁內普通鋼筋不發生滑移，其應變與周圍混凝土應變相同。梁體開裂后，不計受拉區混凝土的貢獻。

（4）梁內普通鋼筋屈服后至破壞前，塑性區段的變形為梁體的主要變形。

1.4 體外預應力筋應力增量計算

極限狀態下，單轉向塊折線型體外預應力混凝土簡支梁的變形簡圖如圖3所示。

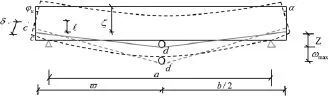
圖3 單轉向塊折線型梁變形圖

單轉向塊梁在受荷前梁端面為斜面，設梁端斜面與垂直方向的夾角為α，由圖3可解算：

設體外力筋的伸長量為△L，忽略梁的軸向變形，由圖可得：

式中：φu很小，sinφu≈φu，即：

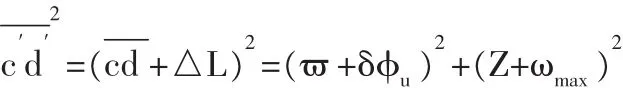
將上式整理成△L的表達式：

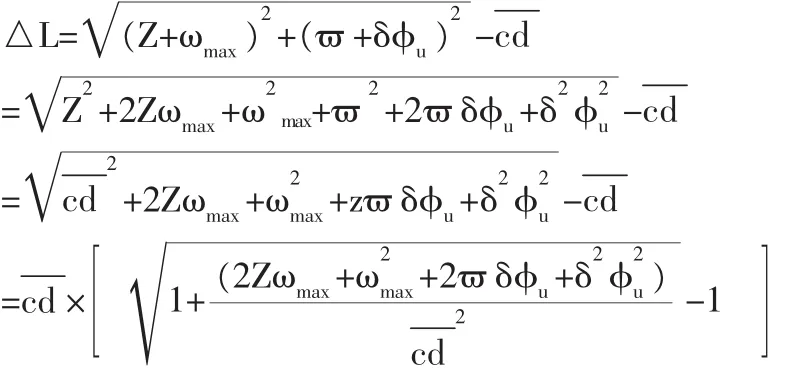
根據數學中的等價無窮小：

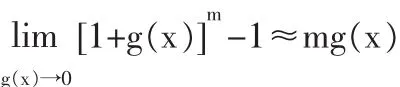
由于δ2φ2u很小，故忽略此項，最終整理為：

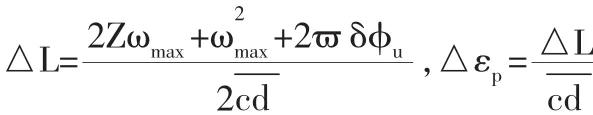
所以，體外預應力筋的應力增量公式為：

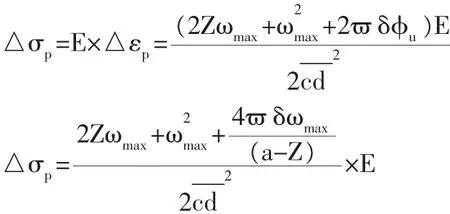
式中：?——錨固點到梁截面形心在豎直方向上的長度；

?——錨固點到轉向塊中心處體外筋在水平方向上的長度；

Z——錨固點到轉向塊中心處體外筋在豎直方向上的投影長度；

H——梁截面高度；

ζ——錨固點到梁上邊緣在豎直方向上的長度；

上式中ωmax一個未知量，其離散型較大，我們這里取經驗值：ωmax/a≈%1，有了ωmax就可以利用公式計算體外筋的應力增量，進而可以計算在極限荷載作用下，單轉向塊體外預應力簡支梁的極限承載力。

1.5 正截面抗彎極限承載力計算

在極限承載力狀態下，體外筋的應力為有效預應力和構件在荷載作用下產生的彎曲變形引起的應力增量（二次效應）兩部分之和。其力學原理與無粘結預應力結構相似，二者的差別在于結構的構造形式不同。

一般設計的體外筋梁為適筋梁，推導其極限承載力是在適筋梁破壞范圍。計算公式如下：

式中：

σu：體外筋的極限應力；

σe：體外筋的有效張拉應力；

△σ：體外筋應力增量

體外預應力混凝土簡支T梁的兩種類型：

第一類T型截面（中和軸在翼緣內）：

第二類T型截面：

式中：x為混凝土受壓區高度，Mu為T梁正截面極限承載力，其它符號意義請見前面有關提示。

2 試驗設計

2.1 基本情況

本次試驗設計了1根單轉向塊體外預應力混凝土T型簡支梁試件。梁長3.2m，計算跨度3.0m，T梁翼緣寬280mm、翼緣高80mm，肋板寬100mm、肋板高200mm，按“強剪弱彎”的原則進行設計。試件基本尺寸及預應力筋形式如圖4所示。

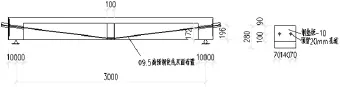
圖4 單轉向塊T梁尺寸圖

混凝土的設計強度等級為C40，每立方米混凝土中水：水泥：沙：石子為200：571：520：1159，由6個150mm×150mm× 150mm的立方體標準試塊在28d標準養護條件下測得其平均抗壓強度實測為52.4MPa。實測φ8抗拉強度為490MPa，φ12抗拉強度為545MPa，高強鋼絞線抗拉強度為2015MPa。

圖5 混凝土立方體試塊受壓

轉向塊為與梁整體澆注在一起的混凝土塊，位置布置于跨中。錨具采用夾片式錨具。在端部張拉端、錨固端（即錨頭局壓區）均預先埋設鋼板（規格：220mm×280mm×10mm）。

施加預應力時，2根索同時張拉（如圖6所示），控制應力為0.50fptk=0.50×1860N/mm2=930N/mm2，分級0.10fptk=186N/ mm2張拉，并跟蹤梁頂混凝土應變，以防混凝土開裂。

圖6 體外預應力施荷圖

試驗時采用單調加載方式進行 （加載方式如圖7所示）。每級荷載級差5.0kN，每級持荷3～6min。梁載荷在極限承載力計算值80%以前，采用力控制；梁載荷在極限承載力計算值80%以前，采用位移控制。位移計布置在梁的加載點位置、跨中和支座部位，來測試試驗梁的撓度情況。

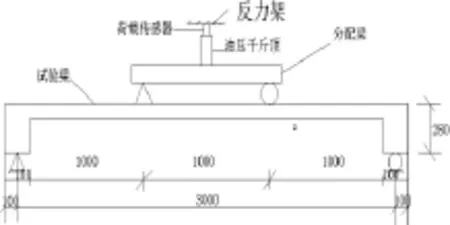
圖7 加載方式

應變片布置在梁頂及分配梁施載點處，以監測沿截面高度試件的應變規律（如圖8所示）；混凝土應變片從上至下均勻布置，加載點處和距跨中左右150mm處黏貼普通鋼筋應變片，體外力筋處布置鋼絞線應變片。位移計和應變采用TDS530系統采集。每級荷載均自動采集撓度、鋼筋應變和混凝土應變。

圖8 試驗梁加載實物圖

2.2 試驗結果

試件TYL加載至35kN時，梁三分點的集中荷載處出現裂縫，繼續加載，跨中純彎段裂縫不斷增多，直至縱筋達到屈服，試件撓度變化明顯，體外預應力鋼束應變增加較快，主要由預應力筋束承擔荷載。

繼續加載，有梁內鋼筋和混凝土脆裂的響聲，試件撓度和應變急劇增加，裂縫不斷向上緣發展，寬度不斷增加。支座產生水平位移，此時跨中撓度22.78mm，卸載后跨中殘余撓度6.76mm。

梁的開裂荷載、屈服荷載、極限荷載如表1所示。

表1 試驗梁特征荷載

2.3 理論值與試驗值對比

從表2可以看出，單轉向塊折線型體外預應力混凝土簡支梁理論值與實際值相差22.8%，理論計算值較實測偏小，說明按本文介紹的理論計算公式偏于保守。

表2 極限荷載理論值與試驗值對照表

3 總結

（1）本文推導了單轉向塊折線型體外預應力混凝土簡支梁的極限承載力計算公式，并與試驗值做了對比，對比結果顯示理論計算公式偏于保守。

（2）與普通鋼筋混凝土簡支梁相比，施加體外預應力鋼絞線后，梁的開裂荷載、屈服荷載、極限荷載均有顯著提高，尤其是梁的開裂荷載。

（3）施加了體外預應力后，簡支梁的剛度有顯著提高。

[1]劉 航，李晨光，白常舉．體外預應力加固混凝土框架梁的試驗研究[J]．建筑技術，1999，30（12）．

[2]李德慧．體外預應力簡支梁受彎性能研究及極限承載力分析[D]．長沙：長沙理工大學橋梁與結構工程學院，2004.

TU378.2

A

2095-2066（2016）22-0217-03

廣東省科技計劃項目（2010A040308005）；廣東省自然科學基金項目（S2012010009615）。

2016-7-23

李英田（1987-），男，河北唐山人，碩士。