基于POD和DMD方法的跨聲速抖振模態分析

寇家慶，張偉偉＊，高傳強

西北工業大學 航空學院，西安 710072

基于POD和DMD方法的跨聲速抖振模態分析

寇家慶，張偉偉＊，高傳強

西北工業大學 航空學院，西安 710072

跨聲速抖振現象是由于非定常跨聲速流動中激波的自激振蕩而引起的結構強迫振蕩，這種現象在跨聲速飛行器中普遍存在，對飛機的結構強度和疲勞壽命有不利影響。基于模態分解的分析方法是進一步發展抖振控制手段的有效工具。本文通過兩類典型模態分析方法（本征正交分解 （POD）和動態模態分解 （DMD））對OAT15A翼型的跨聲速抖振現象進行分析，通過對模態頻率、翼面壓力分布、流場重構誤差等方面的研究，將兩種模態分解方法進行對比。發現基于頻率特征的DMD方法能夠準確捕捉抖振的臨界穩定特征和抖振主頻的典型模態，同時能夠更準確反映流場變量在激波間斷附近隨時間的變化過程；而POD方法盡管在流場重構時具有較小的總體誤差，但對激波附近壓強隨時間的變化歷程擬合較差。

抖振；跨聲速流動；動態模態分解；本征正交分解；激波

跨聲速抖振是由于跨聲速下非定常流動不穩定所引起的結構強迫運動。跨聲速區強烈的激波附面層干擾，使抖振過程中存在著復雜的流動機理和非線性動態特性。這些問題使跨聲速抖振成為航空工程中的研究難點和熱點［1］。針對跨聲速抖振的產生機理，Lee［2］提出的自維持反饋模型給出了合理的解釋，將其理解為激波運動產生的壓力波和尾緣聲波的反饋現象。其他的相關跨聲速抖振研究主要通過試驗［3－4］和數值模擬［5－7］進行，Lee［8］對此進行了全面的綜述。另外，在流體力學研究中，基于試驗或計算樣本，構建非定常流場降階模型（Reduced－Order Model，ROM）是一種重要的研究手段。建立降階模型能夠得到復雜的流體力學現象的主要特征，同時可進一步實現系統機理分析和發展主動／被動流動控制。目前存在兩類典型的非定常流場降階模型［9］：基于系統辨識方法的ROM（如 ARX 模型［10－11］和神經網絡模型［12－14］）和基于流場特征提取方法的ROM（如本征正交分解（Proper Orthogonal Decomposition，POD）［15－16］和動態模態分解（Dynamic Mode Decomposition，DMD）［17－18］）。在兩類模型中，基于流場特征的研究方法在抖振研究中已有部分應用［7］。Chen等［7］對馬赫數Ma＝0．76、雷諾數Re＝1．1×107狀態下18%厚度雙圓弧翼通過大渦模擬（LES）方法進行了數值模擬，并對得到的穩定流場進行POD分解。研究表明根據前兩階POD模態系數得到的頻率與激波運動的頻率一致，且其他主模態的頻率均為一階模態的整數倍。這種ROM不僅能夠實現流場的重構和分析，也能夠進一步發展抖振抑制和抖振流動控制相關的研究。本文針對跨聲速抖振現象，對比了POD和DMD兩種分解方法在抖振分析中的區別和聯系。

POD是最早提出的一種模態分解方法。這種方法將流場分解成若干空間正交模態，按照各個模態的能量（即特征值）大小進行排序，從而選擇出流動主要模態。POD目前已用于研究多種流動問題，例如低雷諾數下圓柱繞流的動態特性［15］和圓柱不穩定線性動力學問題的建模過程［19］等。然而，對于某些復雜流動，可能包含某些對流場動態特性影響很大的低能量特征。近期，Schmid［18］提出了一種通過動態系統特征值估計流動演化并且進行穩定性分析的方法，即DMD。DMD按照頻率對系統進行排序，提取出系統的特征頻率，從而觀察不同頻率的流動結構對流場的貢獻；另外，通過DMD模態特征值可進行流場預測。Rowley等將DMD方法與Koopman算子理論［17］結合，通過無限維線性算子理論使其擴展到非線性流動。DMD在橫向 射 流［20］、帶 襟 翼 機 翼 尾 流［21］和 動 失 速 尾流［22－23］等復雜流動現象上有廣泛應用。結合優化方法或正則化理論，研究者也提出一些改進形式的DMD，如 最 優 化 DMD（optimized DMD，opt－DMD）［24］、最優模態分解（Optimal Mode Decomposition，OMD）［25］和稀疏改進 DMD（Sparsity－Promoting DMD，SPDMD）［26］等。這些改進形式對某些特定的問題可能提取出更好的流動模態。

由于DMD與POD之間存在較多的相關性，因此針對某些復雜流動現象，往往通過POD和DMD進行對比研究。Wan等［20］通過大渦模擬了橫向射流的渦旋流動發展過程，結果表明DMD得到的中立穩定模態以及主導頻率均與LES的計算結果一致，而由于高階POD模態包含多種頻率分量，因此不利于流場的動態分析。Mariappan［22］和Mohan［23］等通過POD和DMD方法分別研究二維翼型和三維機翼的動失速現象，發現DMD模態得到的流動結構對于描述頻域下的流場和提取流動中的主要不穩定模態具有一定優勢。上述研究對比了DMD與POD的區別及聯系。然而，對于具有強非線性特征的跨聲速流動和存在激波間斷的流場，目前沒有結合兩種模態分解方法的研究工作。本文針對典型的超臨界翼型OAT15A，通過兩種模態分解方法對該翼型的跨聲速抖振現象進行分析，進一步研究了兩種模態分解方法在具有激波間斷時，對流場主要動態特點的捕捉能力。

1 POD與DMD方法

POD和DMD都是通過流場各個時刻的流場快照序列，對主要成分進行提取而實現的。

1．1 POD方法

給定N個離散時刻的流場快照（如各個網格點的速度、壓力、密度等），整個流場可分解為基本流動和脈動量的疊加，即

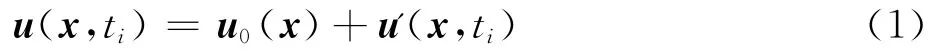
POD的目標是通過正交分解將脈動量用少數POD基和模態系數的乘積表示，即

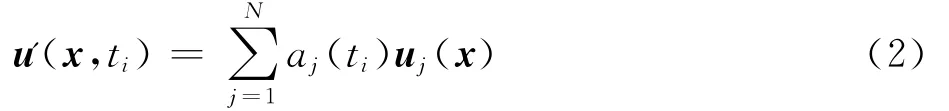
式 中：P ＝ ［u＇（x，t1） u＇（x，t2） … u＇（x，tN）］為減掉均值的快照序列組成的矩陣。由于矩陣C是對稱矩陣，因此具有非負特征值。進而求解特征值問題：式中：特 征 矢 量 A［j］為 模 態 系 數 矩 陣，A［j］＝［aj（t1） aj（t2） … aj（tN）］。POD基定義為

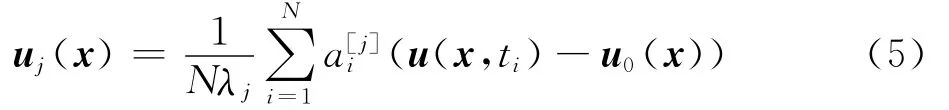
根據特征值λ對模態按照能量進行排序，可以提取出主要的流動模態，通過式（2）可得到任意時刻流場脈動量u＇（x，ti），將其與平均流場相加可得到任意時刻流場。

1．2 DMD方法

通過試驗或數值仿真得到的N個時刻的快照可以寫成快照序列矩陣X和Y，且任意兩個快照之間的時間間隔均為Δt，即

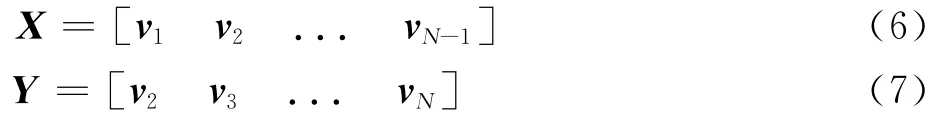
假設流場vi＋1可以通過線性映射A∈RM×M與流場vi表示，即

式（8）中的假設對于任何一個時刻的快照都成立。如果本身動態系統為非線性，則這個過程就是一個線性估計過程，即通過線性假設實現非線性估計。由于存在式（8）的假定，因此有對于秩為r的矩陣X，DMD算法要求尋找矩陣∈Cr×r來代替高維矩陣A，這種替代可通過X的奇異值分解得到，即

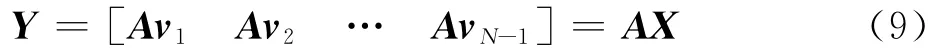
由于奇異值分解，U∈CM×r，UHU＝I；Σ 為對角陣，對角元素從上到下為奇異值從大到小；I為單位矩陣。矩陣槇A的計算可以看做最小化問題：式中為Frobenius范數。因此可將A近似為

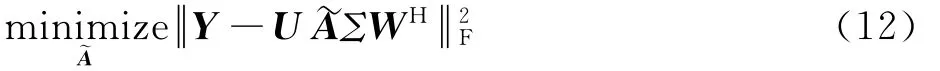
式中：zj為矩陣第j個特征值對應的特征向量。為表達該模態對流場的貢獻，定義模態振幅為。另外一種DMD模態的定義方式可見文獻［27］，形式為

通過上述DMD方法，可以提取出流場的動態模態。

2 非定常流場求解方法

本文的CFD求解器與文獻［5］相同。由于跨聲速非定常流動存在較強的激波附面層干擾，因此本文基于非定常雷諾平均Navier－Stokes（Unsteady Reynolds－Averaged Navier－Stokes，URANS）方程對流場進行求解，采用Spalart－Allmaras（S－A）湍流模型以準確預測抖振現象。通過S－A模型封閉的URANS方程積分形式為

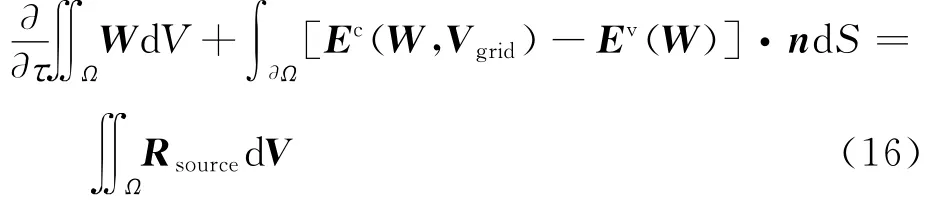
式中：守恒變量為W＝［ρ ρu ρv ρe］T，ρ、u、v、e分別為流體密度、x和y軸的軸向速度和單位質量流體的總內能；無黏通量和黏性通量分別為Ec（W，Vgrid）和Ev（W）；n 為控制體邊界外的法向單位向量；Ω為任意控制體；Ω為該控制體的單元邊界；Rsource＝［0 0 0 0 0 QT］T為源項，QT為S－A湍流模型的源項。CFD求解器求解時，采用格心有限體積法進行求解，通量格式采用Asum＋－up。為求解URANS方程，采用雙時間推進方法。實時間采用二階精度向后差分，偽時間采用隱式對稱Gauss－Seidel迭代，空間離散通過非結構網格實現。求解器的網格無關性驗證和跨聲速算例驗證見文獻［5］。

3 算 例

本文針對OAT15A翼型的跨聲速抖振響應，通過POD和DMD分解提取出主要的模態頻率和能量，用于捕捉激波間斷處的強非線性特征和激波的周期性自激振蕩，同時對比了兩種模態分解方法對于激波間斷的捕捉情況。

該算例的基本條件為：馬赫數Ma＝0．73，雷諾數Re＝3×106，平均迎角α0＝3．5°。無量綱時間步長dτ＝0．073 0，選擇模態分解的快照變量為各網格點壓力。選擇該流動條件是因為抖振可以完全發展且激波振蕩范圍接近20%弦長。圖1展示了升力系數CL的響應歷程，平均流場及特征點如圖2所示，其中流場云圖的橫坐標表示平行于流場的x軸方向坐標，縱坐標為垂直流場的y軸方向坐標，且坐標值關于弦長單位化。圖1中當無量綱時間τ＞60時，激波的周期性簡諧運動引起升力的周期性簡諧變化。在這種抖振狀態下，選擇圖1中標記范圍的695個快照進行模態分解。衡量簡諧運動頻率快慢的無量綱參數為縮減頻率k＝ωb／V，ω為簡諧運動的角速度，b為半弦長，V為來流速度。該無量綱參數是度量非定常效應強弱的特征量。

對圖1的升力系數抖振響應進行Fourier變換，得到圖3中不同縮減頻率下能量大小。在縮減頻率為0．186時具有很強的能量，且兩倍頻的分量（k＝0．372）也包含了一定的能量。這說明當前條件下抖振主頻為0．186，與文獻［4］中試驗測量的結果有一定差異（試驗計算得到的無量綱頻率約為0．207）。但是在 Brunet［28］的研究中發現，在計算抖振邊界的過程中通常需要增加迎角以匹配試驗結果，因此這個縮減頻率在試驗中應該對應更小的抖振迎角。另外，本文的計算結果與文獻［6］的計算結果一致。

3．1 跨聲速流場的POD分解

POD得到的前4階POD模態如圖4所示。可以看到這幾階模態的主要特點都是在激波附近存在間斷，而一階模態附近的間斷更為明顯，其他高階模態則體現了激波附近的更高頻壓力振蕩。

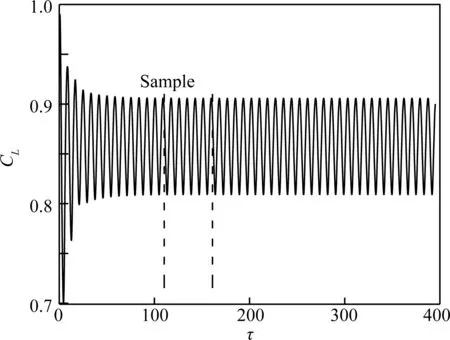
圖1 升力系數隨時間的響應Fig．1 Responses of lift coefficient changing with time

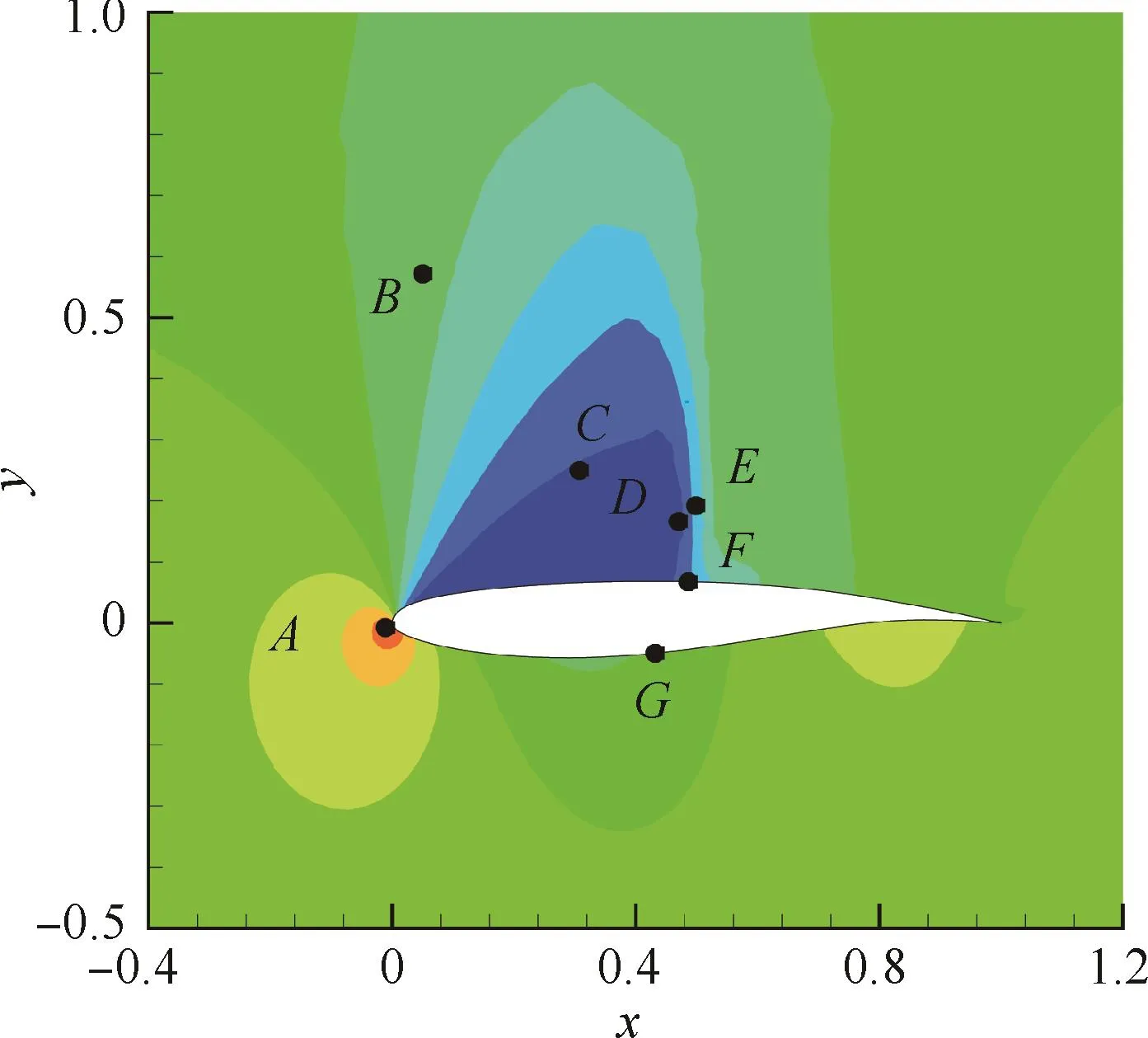
圖2 平均流場壓力云圖及觀測點Fig．2 Pressure contour of mean flow and observation points

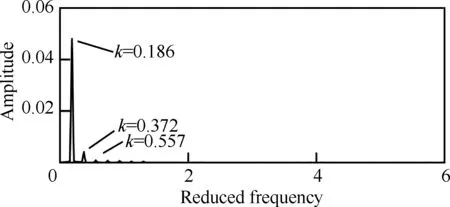
圖3 OAT15A翼型升力系數的Fourier分析Fig．3 Fourier analysis of lift coefficients of OAT15A airfoil

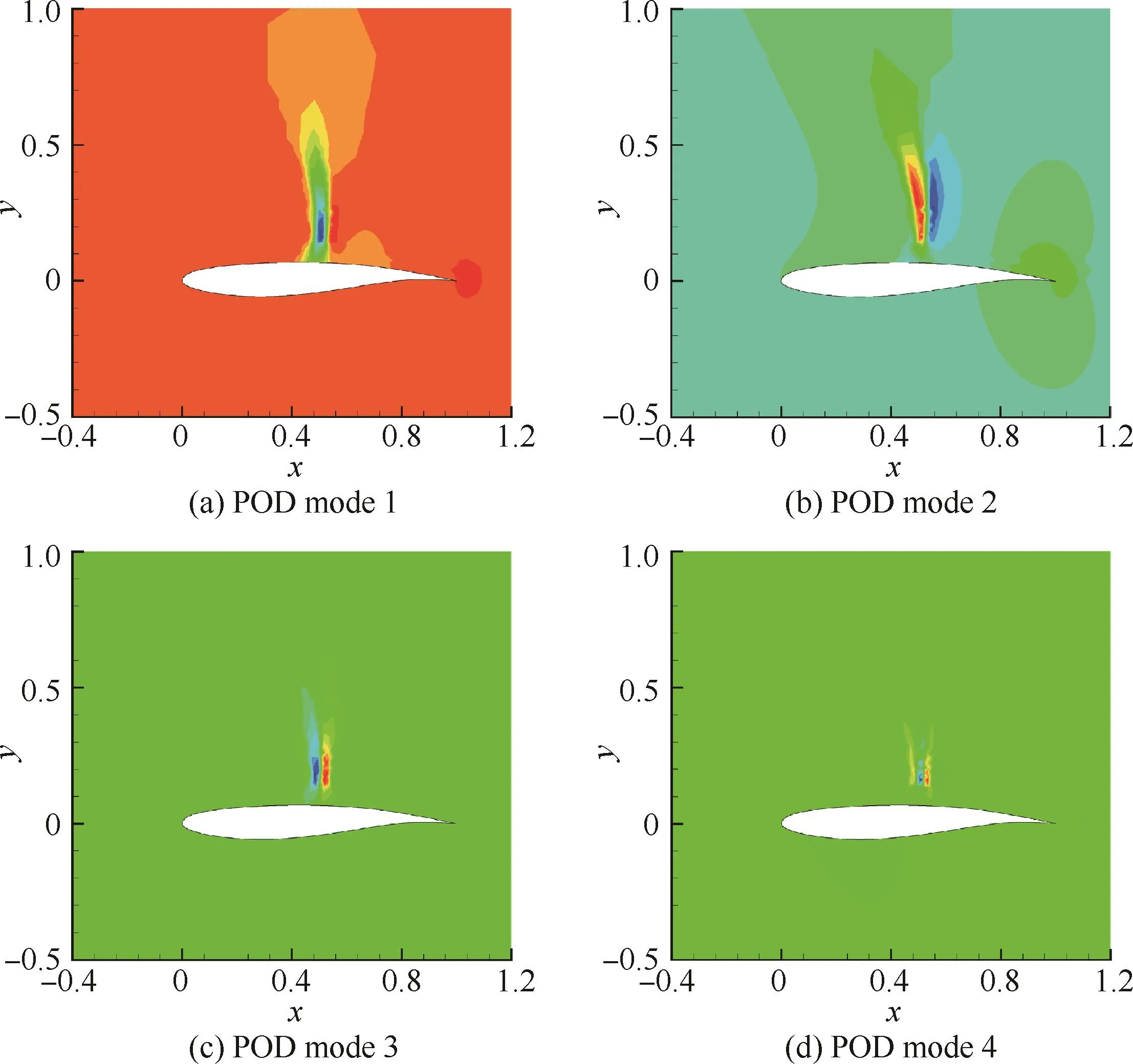
圖4 前4階POD模態Fig．4 The first 4POD modes

將POD特征值進行排序如圖5所示。計算得到排序后的前5階能量已大于99%，即

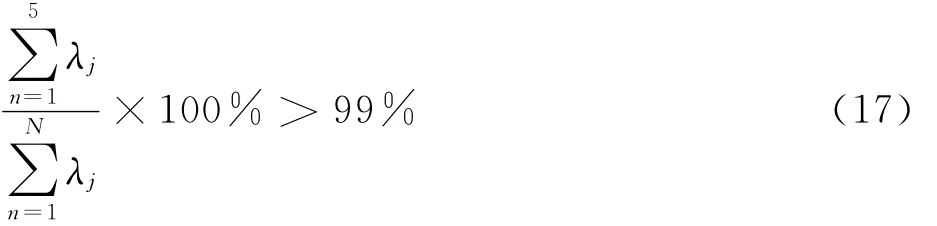
故選擇前5階模態進行重構流場。從圖4中具有主要能量的模態中可以看到，幾個模態均在激波間斷處有較大差異。由于激波的周期性運動，最主要的模態在激波運動產生的間斷范圍內有較大的壓力差，因此存在一個間斷區。第2個和第3個模態捕捉了激波間斷前后的劇烈壓力變化。由于第1個模態捕捉的間斷區較大，而兩個高階模態能夠對間斷區進行進一步調整使其更接近準確流場，因此選擇前5個POD模態已經捕捉了跨聲速抖振狀態下激波的主要特征。

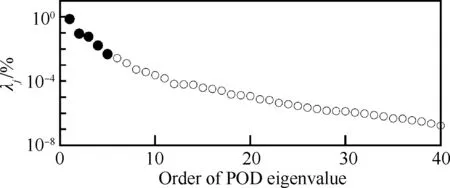
圖5 按照能量排序的POD特征值Fig．5 POD eigenvalues according to energy order

3．2 跨聲速流場的DMD分解

對提取出的流場樣本按照DMD分解，且根據模態振幅αj＝z－1jUHv1對不同頻率的模態進行排序，從而得到各階DMD模態。這種排序方法在一些論文里已有使用［26］。另外還可以根據模態范數進行排序，但是這種方法需要另一種DMD模態的定義［17，21］。采用振幅或模態范數排序的方法能夠按照各個模態對流場的貢獻和影響進行排列，而且也有利于通過這些模態進行流場重構［30］。各個模態的縮減頻率可以通過1．2節提到的Ritz特征值計算得到。DMD提取出的第一個模態為靜態模態，近似于平均流場［24］。其余模態均成對出現，其特征值為共軛復數，因此每一對模態可看做是單個模態［23］。由于POD選擇了5個模態，作為對比，選擇按照振幅排序的前9個DMD模態，以實現流場重構。圖6中顯示了提取模態數目與文獻［26］中定義的損失函數的關系，能夠看出選擇9個模態已足夠使損失函數小于3%（圖6中的實心點）。

模態選擇過程中特征值如圖7所示。圖7（a）中選擇的模態基本靠近單位圓，說明簡諧運動下系統主要處于臨界穩定狀態，這與實際的物理現象一致。從圖7（b）可以看出提取的模態中，第一個模態（靜態模態）的模略大于1，這可能是模態分解中的數值精度造成的。各個模態的增長率和縮減頻率如表1所示。能夠看到由于臨界穩定狀態，各個模態的增長率均很小。對于真實的臨界穩定狀態而言，其增長率應該為零，而計算得到的小增長率同樣可以歸結為數值誤差。各個主要模態的頻率基本上為抖振主頻（基頻）0．186的倍數，這同樣與相關研究的結論一致［18，24］。前3對DMD模態的頻率與Fourier分析得到的主要頻率基本一致，說明通過前7個模態就能把握流動的大部分頻率特征。前7個模態展示在圖8中，且圖中僅展示了各個復模態的實部。從文獻［24］的研究中可以發現，虛部與實部存在一定的相位差異，而在流場特征上區別不大。提取的5對DMD模態中，圖8（a）的第1階靜態模態與均勻流場較為相似，且通過數值計算可知其與均勻流場差異不大。模態2－3則捕捉了激波間斷處周期運動的特性；其他模態同樣一定程度捕捉了激波間斷。從模態2－3到模態6－7，能夠觀察到激波間斷與遠場的差異在不斷變小，說明激波的振蕩主要是由于低頻模態引起，而高頻振蕩的影響相比于低頻成分較弱。

圖6 提取的DMD模態數與損失函數的關系Fig．6 Relationship between extracted DMD modes number and loss function

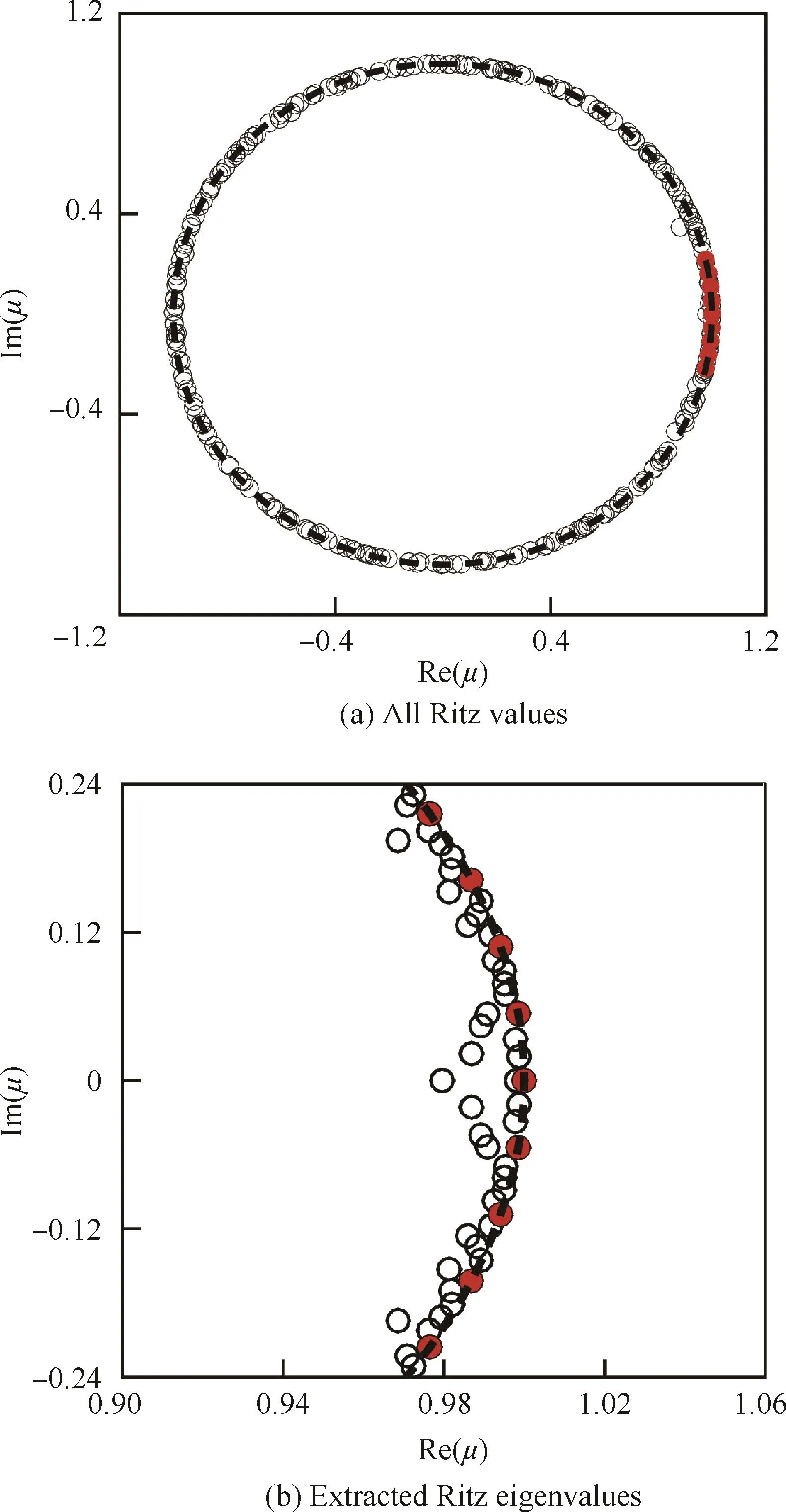
圖7 DMD模態特征值Fig．7 DMD model eigenvalues

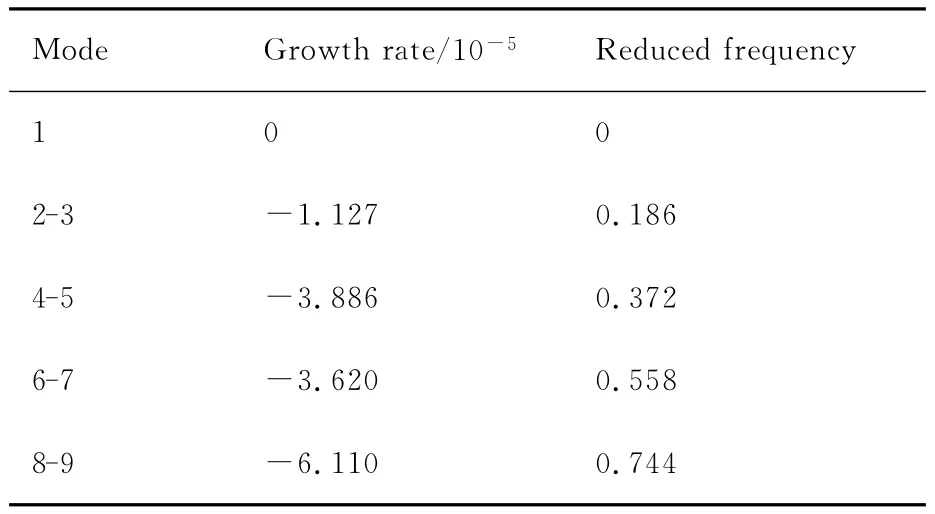
表1 前9階DMD模態及其對應的增長率和縮減頻率Table 1 Growth rates and reduced frequencies of the first 9DMD modes

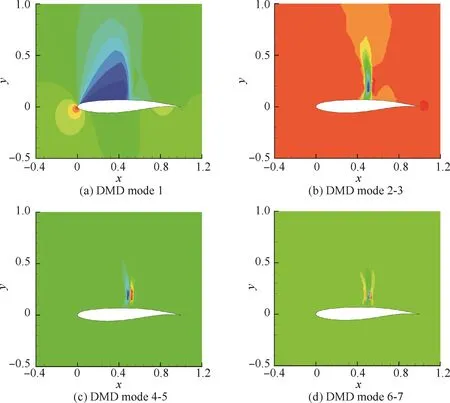
圖8 前7階DMD模態（1個靜態模態和3對共軛模態）Fig．8 The first 7DMD modes with one static mode and three pairs of conjugate mode

3．3 POD和DMD方法的比較

為對比POD和DMD方法分解得到的模態特征頻率，需要對模態系數進行計算。POD的模態系數定義為式（4）；第i時刻的DMD模態系數為（μj）i－1αj。圖9對比了 DMD各階模態系數的實部和POD的各階模態系數。因為DMD模態1為靜態模態，其振幅不隨特征值變化，故并未給出。而主要POD模態的模態系數則并不完全符合簡諧特征，這說明單個POD模態中可能包含多個頻率成分。

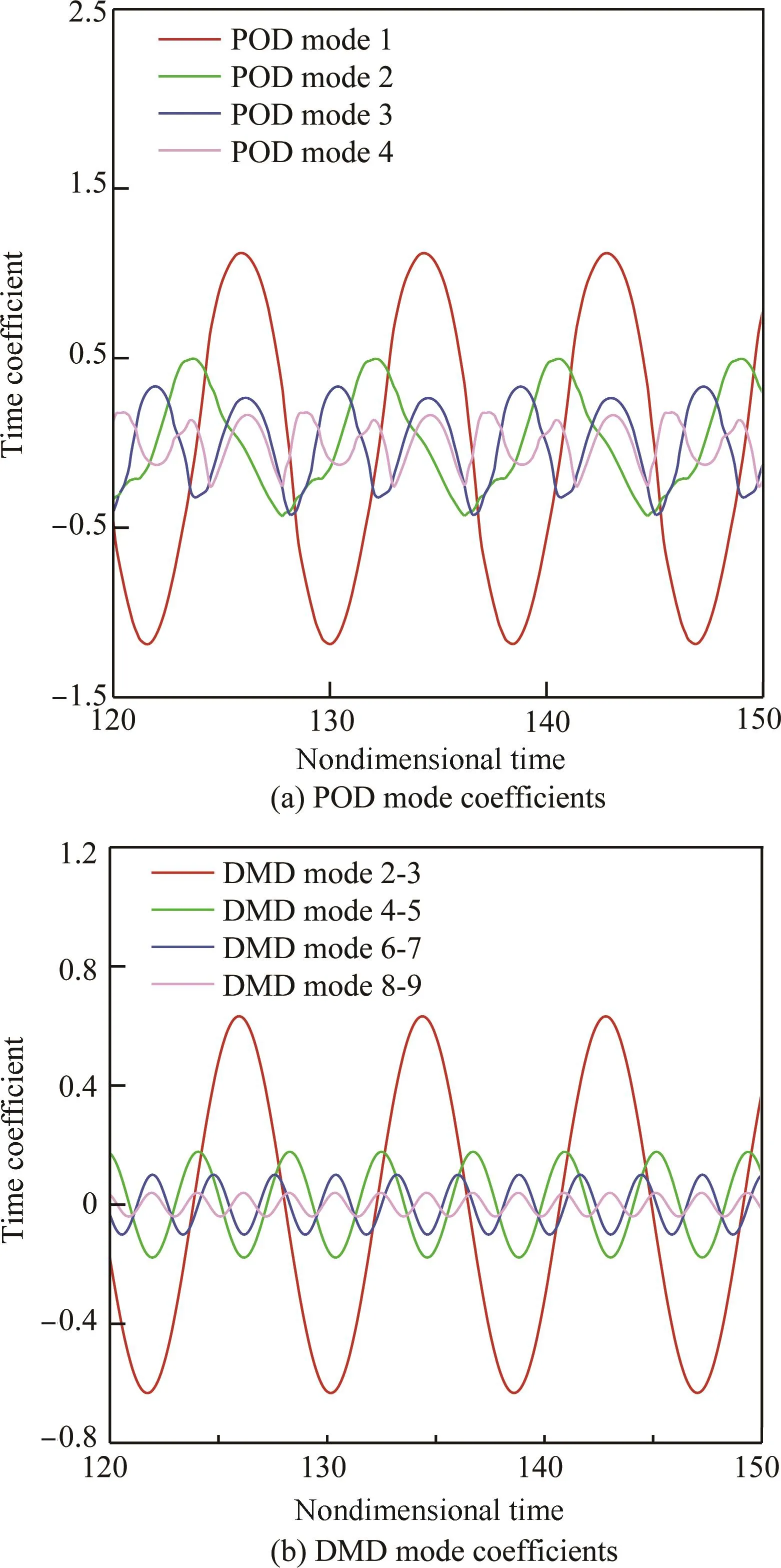
圖9 POD和DMD模態系數變化Fig．9 Evolution of POD and DMD mode coefficients

將模態系數做Fourier分析，可以觀察到不同模態的主要頻率。在圖10（b）展示的DMD模態的Fourier展開結果中，每個模態對應的頻率僅有一個，這在圖8中也已展示。DMD模態按照頻率進行排序，且按照頻率從小到大，幅值在逐漸衰減，說明當前飛行條件下，抖振的主頻為0．186，這與圖3的結論一致，且對于能量較強的頻率0．372，也通過DMD模態4－5體現出來。觀察各個POD模態系數的主要頻率，如圖10（a）所示。可以看出按照能量進行排序的模態可能包含多個頻率成分。雖然各個模態的主頻特征明顯，但是其他頻率流動結構的存在引起了模態系數的非簡諧變化。從POD模態4和POD模態5中，可以看到由于更重要的頻率成分0．372的能量小于0．557，使模態5被排列到模態4之后。而實際上頻率為0．372的流動對流場的影響要大于頻率為0．557的流動。因此，對于跨聲速抖振這種主頻特征明顯的問題，采用POD模態分解可能會忽略某些能量較小，但是接近主導頻率的流動成分。而這些主頻成分對于后續的流場特征分析和流場重構等研究則更為重要。

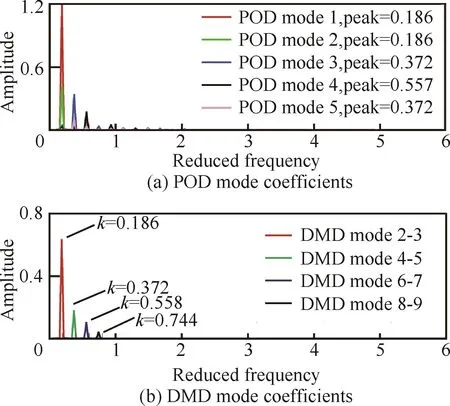
圖10 POD和DMD模態系數的Fourier分析Fig．10 Fourier analysis of POD and DMD mode coefficients

為進一步觀察兩種模態分解方法對流場特征的提取，將得到的POD模態和DMD模態進行流場重構。選擇某兩個特征時刻，無量綱時間分別為t1＝147．407 5和t2＝151．355 5，將兩個時刻的翼型表面壓強p進行對比，如圖11所示，可以看到兩種方法均吻合較好。需要指出圖11中的無量綱壓強p是關于遠場速度和密度進行無量綱化得到的。然而，單從翼型表面壓強來說，并不能獲得足夠的流場對比。因此選擇了圖2中的幾個特征點隨時間變化進行對比，如圖12所示。這個計算過程通過文獻［26］中的模態疊加方法實現。主要選擇了3個特征點（翼型上方點C，激波間斷前方點D和激波間斷后方點E）。能夠看出這3個點均靠近激波間斷，這是為了進一步比較兩模態分解方法對于激波間斷處的捕捉能力。對于除激波附近以外的其他點，當前選擇的模態已足以較為準確的疊加出流場的演化過程。從C點的壓強對比能夠看到，真實的C點處壓強基本呈簡諧變化，通過DMD的各個頻率諧波分量疊加能夠將這種周期性特征反映出來；而POD疊加得到的壓強值也存在周期性，但是在峰值處有較大的偏差；對于激波間斷前的點D，能夠看到因為激波間斷處的周期性運動，點D的壓強變化具有很強的非線性，無論是DMD方法的不同頻率疊加還是POD的能量疊加，都無法準確反映該點的變化趨勢；相比而言，DMD對峰值點的把握比POD準確得多。在光滑下降的區域，DMD和POD都出現了一定程度的波動，但是明顯DMD的誤差相比于POD是可接受的，而DMD疊加產生的振蕩可以歸因于諧波疊加產生的吉布斯效應。激波間斷后方E點的變化也有很強的非線性。能夠注意到DMD準確把握了峰值處的高頻分量，對壓強隨時間的變化趨勢也比POD把握的更準確。由于跨聲速抖振具有明顯的主頻特性，因此相比于POD方法，按照頻率排序得到的DMD模態可以更加精確地捕捉到不同范圍和強度的激波間斷。

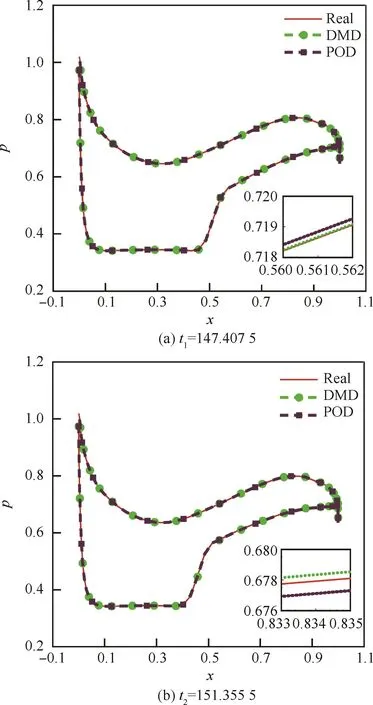
圖11 兩個時刻的翼型表面壓力Fig．11 Pressures on airfoil surface at two time instants

圖13是兩種模態分解方法各個時刻各節點模型的預測與真值的均方根誤差對比。能夠看到

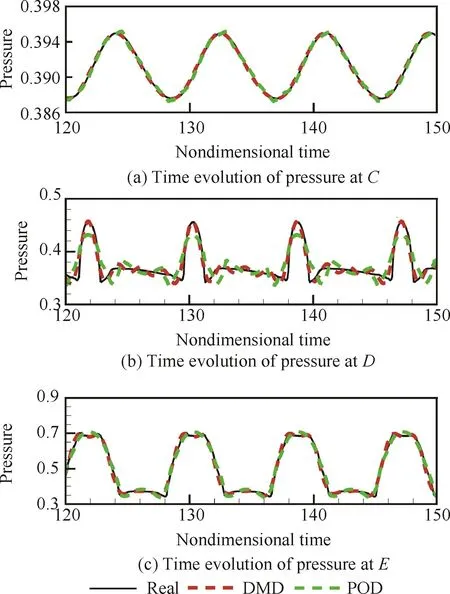
圖12 3個觀察點隨時間的壓強變化Fig．12 Time evolution of pressure at three observation points

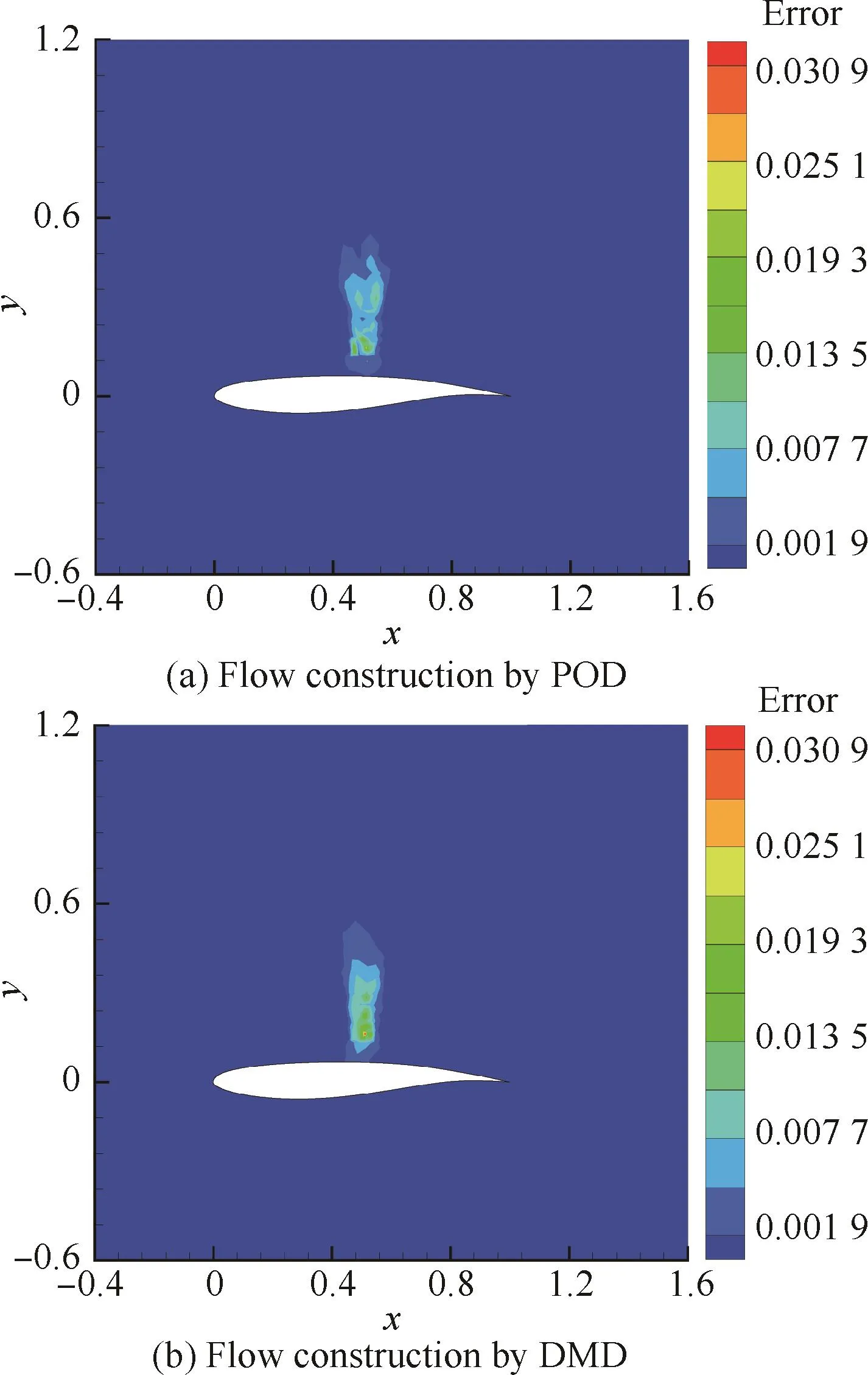
圖13 POD和DMD流場重構的均方根誤差Fig．13 Root mean square errors of flow reconstruction by POD and DMD

較大誤差均在激波間斷處附近。激波間斷處兩種模型差異不大，而DMD得到的降階流場誤差甚至更大。然而從特征點的對比上，能夠發現兩種模態分解方法存在誤差的原因有所不同。由于DMD方法是不同頻率成分的疊加，因此誤差主要來源于激波間斷點疊加過程中的吉布斯現象；POD的誤差主要來自于對極值點不能準確預測，這實際上不利于激波的準確捕捉。綜上所述，從激波間斷捕捉的角度而言，基于頻率成分的DMD方法要好于基于能量成分的POD方法。

4 結 論

1）相比于按照模態能量排序的POD方法，DMD將模態按照頻率排序，得到的是單一頻率的模態，且通過模態特征值可以體現準確捕捉各個模態的頻率及增長或衰減特點，也能夠得到與跨聲速抖振的周期性相關的主要模態。

2）按照能量排序的POD模態系數的時間歷程可能存多種頻率成分，說明幾個主要模態中包含不同的頻率的流動特征，這并不利于研究周期性流動中的主導模態特征，類似跨聲速抖振現象。

3）在激波間斷處附近的流場重構上，POD存在著較小的總體誤差，但是對于流場變量隨時間的變化上不如DMD描述精確。DMD具有較大誤差的主要原因在于不同的單頻模態疊加時，在激波振蕩的位置附近存在吉布斯現象。

［1］ 張偉偉，高傳強，葉正寅．機翼跨聲速抖振研究進展［J］．航空學報，2015，36（4）：1056－1075．ZHANG W W，GAO C Q，YE Z Y．Research advances of wing／airfoil transonic buffet［J］．Acta Aeronautica et Astronautica Sinica，2015，36（4）：1056－1075（in Chinese）．

［2］ LEE B H K．Oscillatory shock motion caused by transonic shock boundary－layer interaction［J］． AIAA Journal，1990，28（5）：942－944．

［3］ MCDEVITT J B，OKUNO A F．Static and dynamic pressure measurements on a NACA 0012airfoil in the Ames High Reynolds Number Facility：NASA TP－2485［R］．Washington，D．C．：NASA，1985．

［4］ JACQUIN L，MOLTON P，DECK S，et al．Experimental study of shock oscillation over a transonic supercritical profile［J］．AIAA Journal，2009，47（9）：1985－1994．

［5］ GAO C Q，ZHANG W W，LIU Y L，et al．Numerical study on the correlation of transonic single－degree－of－freedom flutter and buffet［J］．Science China Physics，Mechanics and Astronomy，2015，58 （8）： 084701－1－084701－12．

［6］ DECK S．Numerical simulation of transonic buffet over a supercritical airfoil［J］．AIAA Journal，2005，43（7）：1556－1566．

［7］ CHEN L W，XU C Y，LU X Y．Numerical investigation of the compressible flow past an aerofoil［J］．Journal of Fluid Mechanics，2010，643（1）：97－126．

［8］ LEE B H K．Self－sustained shock oscillations on airfoils at transonic speeds［J］．Progress in Aerospace Sciences，2001，37（2）：147－196．

［9］ 張偉偉，葉正寅．基于CFD的氣動力建模及其在氣動彈性中的應用［J］．力學進展，2008，38（1）：77－86．ZHANG W W，YE Z Y．On unsteady aerodynamic modeling based on CFD technique and its applications on aeroelastic analysis［J］．Advances in Mechanics，2008，38（1）：77－86（in Chinese）．

［10］ ZHANG W W，YE Z Y．Effect of control surface on airfoil flutter in transonic flow［J］．Acta Astronautica，2010，66（7－8）：999－1007．

［11］ ZHANG W W，LI X T，YE Z Y，et al．Mechanism of frequency lock－in in vortex－induced vibrations at low Reynolds numbers［J］．Journal of Fluid Mechanics，2015，783（1）：72－102．

［12］ 寇家慶，張偉偉，葉正寅．基于分層思路的動態非線性氣動力建模方法［J］．航空學報，2015，36（12）：3785－3797．KOU J Q，ZHANG W W，YE Z Y．Dynamic nonlinear aerodynamics modeling method based on layered model［J］．Acta Aeronautica et Astronautica Sinica，2015，36（12）：3785－3797（in Chinese）．

［13］ ZHANG W W，WANG B B，YE Z Y，et al．Efficient method for limit cycle flutter analysis by nonlinear aerodynamic reduced－order models［J］．AIAA Journal，2012，50（5）：1019－1028．

［14］ KOU J Q，ZHANG W W．An approach to enhance the generalization capability of nonlinear aerodynamic reducedorder models［J］．Aerospace Science and Technology，2016，49（1）：197－208．

［15］ NOACK B R，AFANASIEV K，MORZYNSKI M，et al．A hierarchy of low－dimensional models for the transient and post－transient cylinder wake［J］．Journal of Fluid Mechanics，2003，497（1）：335－363．

［16］ ROWLEY C W．Model reduction for fluids，using balanced proper orthogonal decomposition［J］．International Journal of Bifurcation and Chaos，2005，15 （3）：997－1013．

［17］ ROWLEY C W，MEZIC＇I，BAGHERI S，et al．Spectral analysis of nonlinear flows［J］．Journal of Fluid Mechanics，2009，641（1）：115－127．

［18］ SCHMID P J．Dynamic mode decomposition of numericaland experimental data［J］．Journal of Fluid Mechanics，2010，656（1）：5－128．

［19］ 李靜，張偉偉，李新濤．失穩初期的低雷諾數圓柱繞流POD－Galerkin建模方法研究［J］．西北工業大學學報，2015，33（4）：596－602．LI J，ZHANG W W，LI X T．Researching method of building flow field of initial development stage of low Reynolds number flow past a circular cylinder［J］．Journal of Northwestern Polytechnical University，2015，33（4）：596－602（in Chinese）．

［20］ WAN Z H，ZHOU L，WANG B F，et al．Dynamic mode decomposition of forced spatially developed transitional jets［J］．European Journal of Mechanics B／Fluids，2015，51（1）：16－26

［21］ 潘翀，陳皇，王晉軍．復雜流場的動力學模態分解［C］／第八屆全國實驗流體力學學術會議論文集．廣州：中國科學院南海海洋研究所，2010：77－82．PAN C，CHEN H，WANG J J．Dynamical mode decomposition of complex flow field［C］／8th National Conference on Experimental Fluid Mechanics．Guangzhou：South China Sea Institute of Oceanology，2010：77－82（in Chinese）．

［22］ MARIAPPAN S，GARDNER A D，RICHTER K，et al．Analysis of dynamic stall using dynamic mode decomposition technique［J］．AIAA Journal，2014，52（11）：2427－2439．

［23］ MOHAN A T，GAITONDE D V，VISBAL M R．Model reduction and analysis of deep dynamic stall on a plunging airfoil using dynamic mode decomposition：AIAA－2015－1058［R］．Reston：AIAA，2015．

［24］ CHEN K K，TU J H，ROWLEY C W．Variants of dynamic mode decomposition：Boundary condition，Koopman，and Fourier analyses［J］．Journal of Nonlinear Science，2012，22（6）：887－915．

［25］ WYNN A，PEARSON D，GANAPATHISUBRAMANI B，et al．Optimal mode decomposition for unsteady flows［J］．Journal of Fluid Mechanics，2013，733（1）：473－503．

［26］ JOVANOVIC＇M R，SCHMID P J，NICHOLS J W．Sparsity－promoting dynamic mode decomposition［J］．Physics of Fluids，2014，26（2）：024103－1－024103－22．

［27］ TU J H，ROWLEY C W，LUCHTENBERG D M，et al．On dynamic mode decomposition：Theory and applications［J］．Journal of Computational Dynamics，2014，1（2）：391－421．

［28］ BRUNET V．Computational study of buffet phenomenon with unsteady RANS equations：AIAA－2003－3679［R］．Reston：AIAA，2003．

Modal analysis of transonic buffet based on POD and DMD method

KOU Jiaqing，ZHANG Weiwei＊，GAO Chuanqiang
School of Aeronautics，Northwestern Polytechnical University，Xi’an 710072，China

Transonic buffet is due to the self－sustained oscillations of shock wave in the unsteady transonic flow，which induces the forced periodically motion of the structure．For aircraft in transonic flow，this phenomenon exists commonly，leading to negative effects on the structural strength and fatigue life．Analysis based on mode decomposition is an effective tool for developing buffet control design．In this paper，two typical mode analysis methods，i．e．，proper orthogonal decomposition（POD）and dynamic mode decomposition（DMD），are utilized for analyzing the transonic buffet of the OAT15Aairfoil．Two techniques are compared by studying the frequency of dominant modes，pressure distributions on the surface and the errors of flow construction．Results indicate that because of the consideration of frequency characteristics in DMD，the critical stable characteristics and dominant frequency of transonic buffet are well captured．Besides，DMD method accurately mimic the time evolutions of flow variables near the shock wave．Although POD method provides relatively small errors for flow reconstruction，it performs worse than DMD near the shock wave region，because of the poorer approximation of pressure evolution in time．

buffet；transonic flow；dynamic mode decomposition；proper orthogonal decomposition；shock wave

2015－11－02；Revised：2015－11－26；Accepted：2016－01－06；Published online：2016－01－11 14：55

URL：www．cnki．net／kcms／detail／11．1929．V．20160111．1455．008．html

s：National Natural Science Foundation of China（11572252）；Program for New Century Excellent Talents in University（NCET－13－0478）

V211．1＋5

A

1000－6893（2016）09－2679－11

10．7527／S1000－6893．2016．0003

2015－11－02；退修日期：2015－11－26；錄用日期：2016－01－06；網絡出版時間：2016－01－11 14：55

www．cnki．net／kcms／detail／11．1929．V．20160111．1455．008．html

國家自然科學基金 （11572252）；新世紀優秀人才支持計劃（NCET－13－0478）

＊通訊作者．Tel．：029－88491342 E－mail：aeroelastic＠nwpu．edu．cn

寇家慶，張偉偉，高傳強．基于POD和DMD方法的跨聲速抖振模態分析［J］．航空學報，2016，37（9）：26792－689．KOU J Q，ZHANG W W，GAO C Q．Modal analysis of transonic buffet based on POD and DMD method［J］．Acta Aeronautica et Astronautica Sinica，2016，37（9）：26792－689．

寇家慶 男，碩士研究生。主要研究方向：氣動力降階模型，非定常空氣動力學。

Tel．：029－88491342

E－mail：koujiaqing93＠163．com

張偉偉 男，博士，教授，博士生導師。主要研究方向：氣動彈性力學，非定常空氣動力學。

Tel．：029－88491342

E－mail：aeroelastic＠nwpu．edu．cn

高傳強 男，博士研究生。主要研究方向：流固耦合力學，跨聲速氣動彈性力學。

Tel．：029－88491342

E－mail：gao＿800866＠163．com

＊Corresponding author．Tel．：029－88491342 E－mail：aeroelastic＠nwpu．edu．cn