智能車輛導航系統的模糊控制方法

廖德利

(南京工程學院 電力工程學院， 江蘇 南京 211167)

?

智能車輛導航系統的模糊控制方法

廖德利

(南京工程學院 電力工程學院， 江蘇 南京 211167)

針對背景噪聲及轉彎曲率變化對智能車輛導航系統的橫擺角速度控制精度影響較大的問題，提出一種智能車輛導航系統的模糊控制方法.首先，進行不同坐標系的坐標變換，將目標車輛實際的物理坐標信息變換到易于建模處理的車輛局部坐標系統；接著，通過計算預瞄路徑的非線性函數實時構建了目標虛擬路徑，并給出了車輛目標路徑的橫擺角速度變化率；最后，以期望橫擺角速度和整車質心側偏角作為模糊控制器的輸入，以車輛行駛兩輪差速值作為模糊控制器的輸出，設計導航模糊控制系統.計算機仿真和實測結果表明：文中方法具有較高的控制精度.

智能車輛; 導航系統； 模糊控制； 橫擺角速度； 坐標變換

實時精確的控制技術是智能車輛導航系統的關鍵所在[1]，但是，由于車輛導航系統受側偏信息的影響，導致現有控制技術在不同曲率的道路和不同車速情況下的控制精度差異較大，很難滿足車輛控制系統在不同路況環境下的高精度控制需求[2].王家恩等[3]采用近距離瞄準的方法，但是在實驗場景中的控制精度較差.Kozlowski等[4]基于車輛運動模型構建了模型優化控制方法，但是實時性變差.在此基礎上，Pongsathorn等[5]基于極大極小準則，聯合預瞄點的方法，有效克服了模型漂移誤差的影響，但是無法實現全智能控制反饋[6].為了克服模型漂移的影響，Pentzer等[7]提出了基于期望橫擺角速度的模型控制方法，但是在車輛速度較快的情況下仍然存在模型誤差漂移問題[8].針對現有智能車輛導航控制方法無法滿足控制精度和實時性的折中，本文提出一種新的模糊控制方法.

1 基礎知識

1.1 車輛動力學方程

智能車輛在實際運行過程中的動力學方程[9]可以表示為

(1)

式(1)中：(Xc,Yc)為車輛質心在物理坐標是的坐標;φc為車輛縱軸線與橫向坐標的夾角;v為整車質心速度;ω為車輛在該時刻的橫擺角速度;β為整車質心側偏角.由式(1)可知：車輛的位置信息主要由v，β和ω確定.但是車速v本身就包含了側偏角度信息，因此，主要考慮橫擺角速度和質心速度對車輛導航控制精度的影響.

1.2 車輛坐標變化

為進行仿真分析，主要將車輛的實際物理坐標信息變換到車輛計算仿真的局部坐標系中，如圖1所示.圖1中：Op(Xp,Yp)為車輛物理坐標系OXY中的選擇預瞄點;φp為橫坐標與該點連線的夾角；(Xp,Yp,φp)為車輛和該點在物理坐標系中的相對位置坐標信息；(xe,ye,φe)為在車輛局部坐標系中的相對位置坐標信息.由圖1，車輛局部坐標系OcXcYc中建立車輛質心與點Op的相對位置計算方程[10]為

圖1 車輛物理坐標Fig.1 Vehicle physical coordinate

(2)

式(2)中：xe為預瞄點距離值;ye和φe分別為車輛局部變換坐標系中整車質心與預瞄點之間的橫向差值和方位角差值.

2 模糊控制分析及實現

2.1 預瞄路徑的計算

在OcXcYc坐標系中假設車輛沿著坐標系縱軸方向行駛，則預瞄路徑的非線性方程可以表示為

(3)

在忽略車輛質心側偏角信息的條件下，可以將預瞄路徑方程的已知信息[11]表示為

(4)

式(4)中：ρ為車輛轉彎行駛曲率；A，B，C，D為系數參量.由式(3)，(4)，預瞄路徑為

(5)

2.2 橫擺角速度的計算

為了設計相應的模糊控制模塊，根據式(5)給出的車輛預瞄路徑函數，結合坐標變換的結果，在車輛坐標系中，車輛行駛的曲率[8]為

(6)

(7)

2.3 模糊控制規則

根據模糊控制方法的要求，將ωd的論域集合表示為正(P)、負(N)和零(O)；將β和Δv的論域集合表示為7個模糊子集.其中：ZO表示零值；PB表示正大;PM表示正中;PS表示正小;NB表示負大;NM表示負中;NS表示負小.

根據模糊輸入輸出變量，整個車輛導航系統的模糊控制規則匯總，如表1所示.表1中：β∈[-60°, 60°];Δv∈[-0.2, 0.2],m·s-1;ωd∈[-0.5,0.5],rad·s-1.

表1 模糊控制規則

3 仿真分析

基于Matlab/Simmulink構建了驗證控制算法的仿真模型，車輛整體參數，如表2所示.仿真分析中規定β前行左偏為正，右偏為負，且采用單點預瞄的方法，車速為0.5 m·s-1.為便于定性和定量對比分析，將文中方法的控制精度同文獻[7]的模型控制(model control，MC)方法、文獻[8]的期望橫擺角速度(desired yaw rate，DYR)控制方法進行了對比分析.具體的仿真結果，如圖2～5所示.圖2～5中：s為位移;ωd為橫擺角速度;φe為方位偏差;d為距離偏差值.

表2 仿真參數

圖2 仿真軌跡導航跟蹤結果 圖3 橫擺角速度變化率曲線Fig.2 Simulation track and navigation tracking results Fig.3 Change curve of the yaw angular velocity

由圖2可知：實際的導航曲線包含了直線部分和具有不同曲率的曲線運行部分；在直線部分，3種方法在整體的導航效果上都保持了較高的控制精度.由圖3,4可知：MC方法由于存在模型漂移誤差累積效應的影響，在后期跟蹤結果明顯變差，特別是在具有曲率變化的轉彎路徑時段，由于誤差累積效應的影響，MC方法會產生較大的誤差累積效應，而且無法自適應的適應不同轉彎曲率的變化需求，在第一次出現轉彎運動的時刻開始，MC方法就出現了導航誤差漂移問題；DYR方法由于采用了滑移模塊控制的方法，雖然能夠保持穩定的收斂特性，但是無法收斂到最佳值，主要是因為該方法受背景噪聲干擾比較嚴重，因此，即使跟蹤精度保持了較高的擬合，還存在傳感器本身的噪聲效應；文中方法的實時路徑修正能力克服了傳統的模型誤差累積效應，保持了較高的擬合精度.由圖3～5可知：雖然DYR方法也保持了較高的擬合精度，但是該方法無法收斂于0，加上控制參量的模糊控制，本身可以消除傳感器的噪聲擾動，保持了較好的0值收斂狀態.

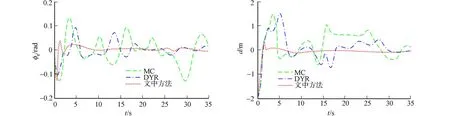
圖4 方位偏差曲線 圖5 距離偏差曲線Fig.4 Azimuth deviation curve Fig.5 Distance deviation curve

4 結束語

針對智能車輛導航控制問題，提出了一種橫擺角速度的模糊控制方法.該方法首先推導分析了期望橫擺角速度變化率.通過將車輛物理坐標變換到車輛局部坐標，在實時構建目標虛擬路徑的基礎上計算了期望橫擺角速度變化率.并以期望橫擺角速度變化率和整車質心側偏角作為模糊控制器的輸入，行駛車輛兩輪的差速值作為模糊控制器的輸出，設計了模糊控制系統.計算機仿真驗證了文中方法具有較高的控制精度，在直線和曲線定位導航兩種情況下均保持了較高的導航精度和穩定性.

[1] 李剛,韓海蘭.四輪輪轂電機電動車橫擺力矩參數自調整模糊控制[J].華僑大學學報(自然科學版),2015,36(4)：365-370.

[2] 宋國杰.采用自適應模糊PID的二階倒立擺控制[J].華僑大學學報(自然科學版),2016,37(1)：74-78.

[3] 王家恩,陳無畏,王檀彬,等.基于期望橫擺角速度的視覺導航智能車輛橫向控制[J].機械工程學報,2012,48(4)：108-115.

[4] KOZLOWSKI K,PAZDERSKI D.Modeling and control of a 4-wheel skid-steering mobile robot[J].International Journal of Applied Mathematics and Computer Science,2004,12(4):477-496.

[5] PONGSATHORN R,MASAO N,MOTOKI S.Lane keeping control strategy with direct yaw moment control input by considering dynamics of electric vehicle[J].Vehicle System Dynamics,2006，44(3):192-201.

[6] ANI O A,XU He,SHEN Yiping,et al.Modeling and multi-objective optimization of traction performance for autonomous wheeled mobile robot in rough terrain[J].Journal of Zhejiang University,2013,14(1):11-29.

[7] PENTZER J,BRENNAN S,REICHARD K.Model-based prediction of skid-steer robot kinematics using online estimation of track instantaneous centers of rotation[J].Journal of Field Robotics,2014,31(3):455-476.

[8] YANAGIYA M,TOMITA K,TSUGAWA S.Effects of field of view on lateral control performance in a vision-based autonomous vehicle[J].JSAE Review,1999,20(4):499-504.

[9] 高振海.汽車方向預瞄式自適應PID控制算法[J].機械工程學報,2004,40(5):101-105.

[10] 孟慶寬,仇瑞承,張漫,等.基于改進粒子群優化模糊控制的農業車輛導航系統[J].農業機械學報,2015,46(3)：29-36.

[11] YU W,CHUY O,COLLINS E G,et al.Analysis and experimental verification for dynamic modeling of a skid-steered wheeled vehicle[J].IEEE Transactions on Robotics,2010,26(2):340-353.

(責任編輯： 陳志賢 英文審校： 崔長彩)

Fuzzy Control Method of Intelligent Vehicle Navigation System

LIAO Deli

(School of Electric Power Engineering, Nanjing Institute of Technology, Nanjing 211167, China)

In view of the intelligent vehicle yaw angular velocity poor control precision problem, which come from the background noise and turn the curvature change, this paper proposes a fuzzy control method of intelligent vehicle navigation system. Firstly, this method transforms the vehicles physical coordinate to the vehicle local coordinates. Secondly, the method calculates and analysis the yawing angular velocity change rate of vehicle target path, which based on building target virtual path in real-time. Finally, a fuzzy controller is set with desired yaw angular velocity change rate and the vehicle mass center side-slip angle deviation as in put, and differential speed value of vehicle as output. The computer simulation analysis and experiment shows that the proposes method has high control accuracy and anti-interference ability.

intelligent vehicle； navigation system; fuzzy control; yaw angular velocity; coordinate transformation

10.11830/ISSN.1000-5013.201606021

2016-10-20

廖德利(1975-)，男，實驗師，博士，主要從事電氣工程及其自動化的研究.E-mail:ldelly@163.com.

江蘇省高校自然科學基金資助項目(15KJB470005)

TP 242.6; TP 391.41

A

1000-5013(2016)06-0766-04