基于重采樣粒子濾波的目標跟蹤算法研究

廖雪陽+任宏光+章惠君

摘要： 基于傳統粒子濾波的機動目標跟蹤方法針對非線性、 非高斯系統有較好的估計性能， 但是存在粒子退化現象。 利用殘差重采樣算法， 可以有效克服粒子濾波的退化問題。 本文針對殘差重采樣算法作進一步研究， 提出了一種改進的殘差重采樣粒子濾波算法。 該方法在殘差重采樣基礎上進行改進， 可以避免殘差重采樣中關于殘留粒子的重采樣問題， 在保證精度的前提下提高運行效率， 減少運算復雜程度。 仿真實驗結果表明該算法與殘差重采樣粒子濾波相比提高了目標跟蹤的實時性， 并且隨著粒子數的增加， 這種優勢表現得更加明顯。

關鍵詞： 粒子濾波； 殘差重采樣； 運行效率； 目標跟蹤； 粒子退化

中圖分類號： TJ765； TP391.41文獻標識碼： A文章編號： 1673-5048（2016）05-0025-04

Abstract： The method of target tracking based on traditional particle filter performs well when estimating nonlinear/nonGaussian systems， however particles degeneration can occur. The particles degeneration can be overcome by using residual resampling algorithm. Through the research on residual resampling algorithm， an improved residual resampling particle filter algorithm is presented in this article. The method which improves the residual resampling algorithm can avoid the resampling of residual particles， thus improving running efficiency and reducing computational complexity. Simulation results show that the effect of realtime target tracking of this improved algorithm is higher than that of residual resampling particle filter. When there are more particles， the efficiency is more outstanding.

Key words： particle filter； residual resampling； running efficiency； target tracking； particle degeneration

0引言

為了解決對目標的跟蹤[1]問題， 需要對目標的信息進行濾波， 當前工程中卡爾曼濾波算法應用最為廣泛。 當系統為線性系統并且狀態為正態分布時， 狀態的期望概率密度函數依然是正態分布， 這一類估計問題可以利用卡爾曼濾波（Kalman Filter， KF）[2-3]來較好地解決。 當狀態空間具有非線性或非高斯特點時， 卡爾曼濾波算法的精度會大幅下降。 采用擴展卡爾曼濾波（Extended KF， EKF）[4-5]和無跡卡爾曼濾波（Unscented KF， UKF）[6]可以解決某些形式的非線性、 非高斯條件下目標狀態的估計問題。 但因為其對系統模型有很強的限制性， 需要目標的狀態模型和對目標的觀測模型都近似于線性， 濾波結果才有可能逼近真實狀態。 針對此問題以隨機采樣法近似為基礎的粒子濾波（Particle Filter， PF）[7-8]算法， 由于具有粒子散布特點， 可以在真值附近一定范圍內迅速捕捉到真實狀態， 在提高跟蹤系統的收斂性和快速性方面具有較大優勢[9]。

然而傳統的粒子濾波存在粒子退化的不足， 即每個粒子經過多次循環計算之后， 權重的方差會不斷變大， 使得很小部分后代樣本的權值極大， 而絕大多數后代樣本的權值卻極小， 導致很多運算花費在計算影響力小的粒子上， 同時粒子也失去多樣性。 當前針對粒子衰退問題， 主要的應對辦法是選取更接近模型的重要密度函數和對重采樣算法優化。 Gordon[10]提出了多項式重采樣算法， 其核心思路是減去權值小的粒子， 將權重大的粒子留下來， 這從很大程度上解決了粒子多樣性的衰退問題。 Liu[11]等人又根據多項式重采樣算法提出了殘差重采樣算法。 由于殘差重采樣可以遍布到系統狀態的所有粒子， 所有粒子都存在被復制的幾率， 擴大了系統狀態的多樣性。

本文引入另一種殘差重采樣與粒子濾波相結合算法， 即改進的殘差重采樣粒子濾波（Improved Residual Resampling Particle Filter， IRRPF）算法， 其對之前的算法進行了優化， 對機動目標進行跟蹤。 該算法不會產生殘差重采樣中的剩余粒子， 不進行二次重采樣， 在保證精度的前提下減少運算次數， 從而減少時間。

1粒子濾波算法

粒子濾波[12]是一種基于蒙特卡洛仿真的濾波算法， 相對于卡爾曼濾波算法， 能更好應對各種系統的估計問題， 特別是系統的非線性度較高的情況。 粒子濾波實質是貝葉斯算法的一種表現形式， 利用狀態量中一組隨機樣本集（粒子）來模擬真實狀態的后驗概率密度函數， 從而得到下一刻的狀態估計。 其主要思想是利用這些采樣點和權值來獲得最小方差的狀態估計， 是一種基于仿真的統計濾波方法。

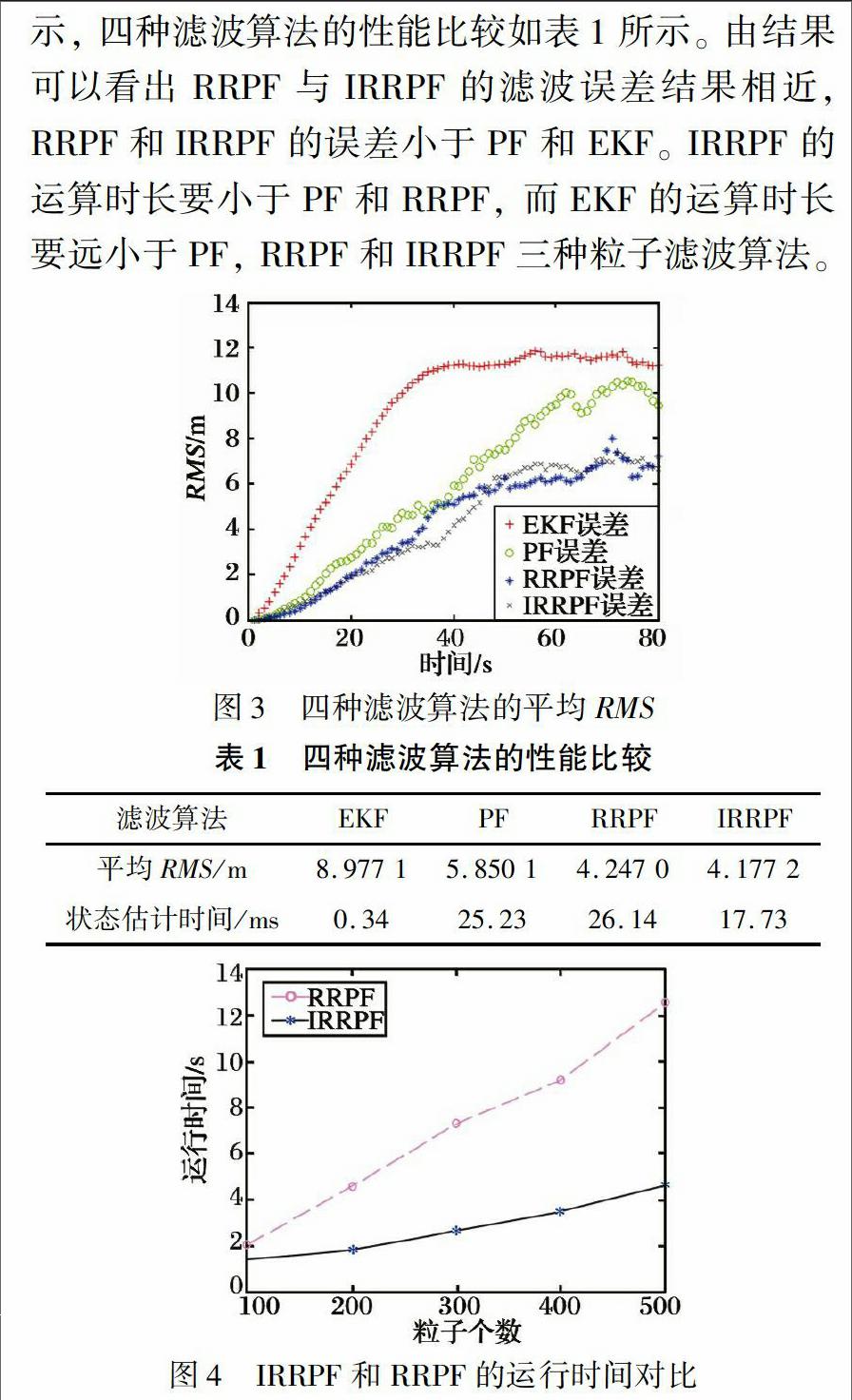
對EKF， PF， RRPF， IRRPF四種濾波算法進行100次蒙特卡洛仿真的平均RMS對比如圖3所示， 四種濾波算法的性能比較如表1所示。 由結果可以看出RRPF與IRRPF的濾波誤差結果相近， RRPF和IRRPF的誤差小于PF和EKF。 IRRPF的運算時長要小于PF和RRPF， 而EKF的運算時長要遠小于PF， RRPF和IRRPF三種粒子濾波算法。

表1四種濾波算法的性能比較濾波算法EKFPF RRPFIRRPF平均RMS/m8.977 15.850 14.247 04.177 2狀態估計時間/ms0.3425.2326.1417.73不同粒子數情況下， IRRPF和RRPF的總運行時間對比如圖4所示， 可見隨著粒子數目的增加， IRRPF的運行效率更加突出。

4結論

在基于粒子濾波算法的目標狀態估計問題中， 重采樣是粒子濾波的重要步驟， 對誤差結果和運行速度起重要影響。 本文針對重采樣過程， 提出了一種改進殘差重采樣算法。 仿真結果表明， 該算法不會產生剩余粒子， 能減少運算復雜程度， 一定程度降低了運算時長， 并且當粒子數目變多時， 優化后的殘差重采樣粒子濾波算法相對用時更少， 效率更高。

同時也需要指出， 粒子濾波的主要優勢是通用性， 相對于卡爾曼濾波算法， 粒子濾波算法必須以大量粒子為基礎， 即使對其進行一些改進， 運算開銷也比較大。 對于某些簡單的線性或較弱的非線性問題， 卡爾曼濾波已經能達到較理想的效果， 采用粒子濾波手段所能獲得的額外效果不大。 因此， 在具體應用時， 應根據需要處理問題的特點對擬采用的方法進行合理選擇。

參考文獻：

[1] 嚴運彪， 何廣軍， 付國慶.改進型自適應濾波算法在目標跟蹤中的應用[J].航空兵器， 2008（5）： 30-37.

[2] 周宏仁， 敬忠良. 機動目標跟蹤[M]. 北京： 國防工業出版社， 1991.

[3] Kalman R E. A New Approach to Linear Filtering and Prediction Problems[J]. Journal of Fluids Engineering， 1960， 82（1）： 35-44.

[4] Sunahara Y. An Approximate Method of State Estimation for Nonlinear Dynamical Systems[J]. Journal of Fluids Engineering， 1969， 92（2）： 382-397.

[5] 黃曉雷， 牛申閣.擴展卡爾曼濾波在無人機航跡控制系統中的應用研究[J].航空兵器， 2008（2）： 11-17.

[6] Uhlmann J， Julier S， DurrantWhyte H F. A New Method for the Nonlinear Transformation of Means and Covariances in Filters and Estimators [J]. IEEE Transactions on Automatic Control， 2000， 45（3）： 478-481.

[7] 朱志宇.粒子濾波算法及其應用[M].北京： 科學出版社， 2010.

[8] Cappe O， Godsill S J， Moulines E.An Overview of Existing Methods and Recent Advances in Sequential Monte Carlo[J]. Proccedings of the IEEE， 2007， 95（5）： 899-924.

[9] 占榮輝， 張軍.非線性濾波理論與目標跟蹤應用[M] . 北京： 國防工業出版社， 2013.

[10] Gordon N J， Salmond D J， Smith A F M. Novel Approach to Nonlinear/NonGaussian Bayesian State Estimation [J]. IEE Proceedings F （Radar and Signal Processing）， 1993 ， 140（2）： 107-113.

[11] Liu J S， Chen Rong. Sequential Montecarlo Menthods for Dynamic Systems[J]. Journal of American Statistical Association， 1998（93）： 1033-1043.

[12] 吳寶成.粒子濾波重采樣算法研究及其應用[M].哈爾濱： 哈爾濱工業大學出版社， 2006.

[13] 張萬里， 何金剛.交互多模型的Rao-Blackwellized粒子濾波算法在多目標跟蹤中的應用[J].航空兵器， 2014（4）： 3-7.

[14] 黃小平， 王巖.卡爾曼濾波原理及應用[M].北京： 電子工業出版社， 2015.

[15] Van der Merwe R， De Freitas N， Doucet A，et al. The Unscented Particle Filter [M]. England： Cambridge University Press， 2000： 1-40.

[16] 王龍， 夏厚培.改進粒子濾波算法及其在目標跟蹤中的應用 [J].信息技術， 2013（2）： 121-123.