柴油機缸內三維動網格和流場數值模擬程序開發

劉曉剛，明平劍，張格健，張文平

(哈爾濱工程大學 動力與能源工程學院，黑龍江 哈爾濱 150001)

?

柴油機缸內三維動網格和流場數值模擬程序開發

劉曉剛，明平劍，張格健，張文平

(哈爾濱工程大學 動力與能源工程學院，黑龍江 哈爾濱 150001)

現較為成熟的CFD仿真軟件均為國外所有，國內缺乏相應的知識產權。為此，本文自主研發了一套仿真程序，對內燃機缸內三維工作過程進行數值模擬。本文建立了動態層網格模型和匹配的任意邊界模型，采用有限體積方法離散流場控制方程，通過SIMPLEC算法求解NS方程，基于FORTRAN語言開發了一套內燃機缸內流場仿真軟件。對內燃機的缸內空氣純壓縮和膨脹過程做了仿真分析，計算結果表明，缸壓曲線、缸內溫度曲線與應用商業軟件PUMPLINX、FLUENT計算結果基本吻合,證明動網格模型和流場數值模擬方法正確，本文的程序有進一步市場應用的前景。

內燃機；運動網格；CFD；數值模擬；程序開發；軟件仿真

內燃機缸內流場數值模擬主要是借助CFD手段預測缸內的流動形式，從而在設計階段可預先改進進氣形式或燃燒室形狀，形成更好的缸內氣流狀態以提高燃燒效率和降低污染物排放，在現代內燃機設計和預先研究中發揮了越來越重要的作用[1]。而目前國內的內燃機設計上主要采用市面上較為流行的商用軟件，如KIVA系列軟件[2]、AVL Fire軟件、STAR-CD軟件、ANSYS Fluent軟件和新興的CONVERGE軟件等，購買和升級費用昂貴，沒有獨立的知識產權，一直受制于人，阻礙了中國內燃機行業的發展。

哈爾濱工程大學自主研發的基于非結構化網格的通用輸運方程求解軟件[3-5](general transport equation analysis,GTEA)采用有限體積方法離散流場控制方程，通過SIMPLEC算法求解NS方程和分離式變量求解方法，目前可以較為精確的求解二維和三維、層流和湍流的流場流動問題。本文在該軟件的基礎上，根據內燃機的氣缸往復直線運動形式建立了動態層網格模型和匹配的任意邊界模型，并實現了其與流場求解器的耦合計算，形成了一套內燃機缸內流場專業化仿真軟件。

1 數學模型

數值計算中數學模型可分為計算域的幾何信息模型和數學控制方程模型。

1.1 運動網格模型

動態層模型[5]是利用增加或刪減網格層來適應邊界的運動，該方法對網格的劃分及邊界的運動形式要求較高，邊界運動主要為往復式直線運動，網格需要在動邊界運動方向上分層。程序實現時首先要建立結構體數組來保存每層網格的單元和節點信息，以便進行網格層間拓撲信息的查找，之后再根據計算域是膨脹還是壓縮來做網格層的加減，如下圖1所示，只對最下層的網格做加減層操作，以最大程度保持網格原有質量。通過網格節點坐標替換及網格標記阻斷相結合的方法來滿足增減網格層時網格拓撲結構的變化，減層時1、2、3、4單元被阻斷，也就是不參與計算，F、G、H、I、J節點替換A、B、C、D、E節點坐標；加層時增加1、2、3、4單元，增加A、B、C、D、E節點，并替換F、G、H、I、J節點坐標。

圖1 增減網格層時層動邊界網格拓撲結構變化Fig.1 Topological structure change of the moving boundary mesh when the grid layer is changed

匹配的任意邊界網格模型[6]，即商用軟件中的r任意邊界模型，是指由于相對運動等原因在同一位置有兩個邊界存在，再通過其上的邊界面找到對應關系以傳遞流場中的信息，以按內部單元面處理。由于動態層網格在三維情況下只適用于規則的六面體或者三棱柱網格單元，且本文只對初始網格進行編號，所以要將整個計算域劃分為氣缸區域和燃燒室區域，在兩個區域結合處采用任意邊界面的處理方法。本文為處理方便在網格劃分時將這兩個邊界上的網格一一對應(在Gambit軟件中選中Link mesh face選項)，這樣兩個邊界面上的所有網格幾何信息全部相同，單元面間的相交判斷就可以通過邊界單元面的中心坐標是否相同來實現，進而確定邊界單元面間的對應關系和所屬單元。

1.2 流場控制方程

流體的運動要滿足基本守恒定律，其控制方程組是各種CFD軟件求解的基本數學模型，通用輸運方程的積分形式可寫為

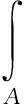
(1)

式中:ρ是流體密度，U和Ub分別是流體和網格面運動速度，圖1中紅色運動邊界處的邊界單元面需要計算其Ub，本文采用上一時間段平均移動速度計算，n是單元面的外法線方向單位向量，V和A分別為網格單元體積和單元面的面積，φ為通用形式控制方程的求解變量，Γφ為對應的擴散系數，Sφ為相應的源項。各方程的具體形式如表1所示。

表1 擴散系數和源項

表中，μeff為有效粘性系數，求解層流問題時μeff=μl，求解湍流時μeff=μl+μt，H為流體總焓，λ為導熱系數，cp為定壓比熱，Prt為湍流普朗特數，τ為流體所受切應力，k-ε系列湍流方程同樣可以寫為上述形式，本文算例沒有采用湍流方程，這里不再贅述。

2 數值方法

2.1 控制方程離散

時間項的離散計算類似于一階常微分方程，本文采用歐拉隱式格式對其進行計算，近似可得離散形式為

(2)

式中，Δt為計算時間步長、(ρVPφ)o為上一時刻值，F(φ,t)為通用輸運方程中除時間項外的所有其他項當前時刻值之和，所以這種格式稱作為隱式格式。

通過對對流項的離散，其可以近似等于各單元面上的對流通量之和：

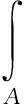
(3)

式中：nf為當前單元所含有的單元面個數，fj為通過該單元第j個單元面的流量，當流速與單元面外方向n相同時為正，否則為負。單元面上變量值φj的取值取決于對流項采用的格式，常采用的一階迎風格式：

(4)

則離散后的對流項最終可寫為

(5)

擴散項的離散要稍微復雜一些，將變量梯度分為法向n和交叉向τ兩部分，略去中間計算過程，最終可得：

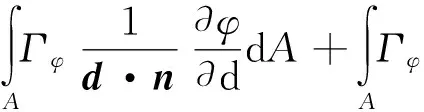
(6)

式(6)中右端第一項為法向擴散部分，第二項為交叉向擴散部分，近似離散為

(7)

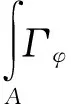
(8)

(9)

通過有限體積法離散流體通用控制方程，最終可得代數方程組目標形式為

(10)

式中：φP和φPj分別為當前單元和第j個相鄰單元的變量值，ap和aj分別為代數方程中當前單元和相鄰單元變量系數，bp為代數方程源項，本文通過代數多重網格和共軛梯度法求解代數方程組。

2.2 時間項與對流項特殊處理

為方便程序計算，要對時間項和對流項進行特殊處理。采用一階迎風格式離散對流項，可進一步寫成如下形式：

(11)

可知，當fj>0時，fj=fout；當fj<0時，fj=fin。同樣經過上述處理，忽略源項，離散后的連續方程可寫為

(12)

將其代入式(11)，對流項最終可得：

(13)

式中:fin只能等于零或-fj，所以可讓fin=-max(0, fj)。

離散后的時間項可進一步整理得：

(14)

最后將時間項和對流項合并在一起，可得：

(15)

根據上述各項對代數方程組的貢獻，經整理各系數可表示為

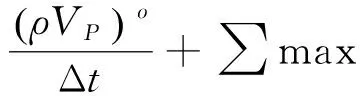
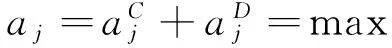
這樣就會對每個方程形成代數方程組，為使方程求解穩定，本程序采用求解小量形式進行求解，式(10)可變為

(16)

式中：φ'=φ-φo。GTEA采用分離式變量求解方法，即逐一求解各個方程組，本文采用的共軛梯度法和代數多重網格法來求解代數方程組，進而求得各變量。

2.3 非結構化網格SIMPLEC算法

動量預測是SIMPLE系列算法[7]的第一步，其主要思想是根據初始給定的壓力p*和ρ*，通過求解動量方程得出預測步的U*。將動量方程中的壓力梯度項提出進行單獨處理，可得離散后動量方程的代數方程形式為

(17)

則可通過上式求得預測步的各單元中心的速度。

壓力修正的主要思想是利用動量預測得出的單元中心的速度，再用求解動量方程相似的形式來計算網格面上的速度，即動量加權或Rhie-Chow插值的方法；并采取壓力、速度、密度修正的方法，用壓力修正量表示速度和密度的修正量，最后修正單元面的流量，將其代入連續方程。SIMPLEC算法得到的壓力修正量和速度修正量之間的關系為

(18)

省略中間計算,最后得出壓力修正方程的形式如下

(19)

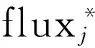
動量修正的主要目的是通過壓力修正方程求出的壓力修正量來修正速度和壓力。雖然速度修正量與壓力修正量之間的關系是通過動量方程求出，但通過壓力修正方程之后，修正后的速度是嚴格滿足連續方程的，修正后的壓力也同樣滿足動量方程。程序中修正的公式為

(20)

(21)

而最后修正的密度是通過狀態方程和已修正后的速度計算得出。

圖2所示為GTEA軟件的計算流程圖。

圖2 程序計算流程圖Fig.2 Program calculation flow chart

3 算例驗證

為驗證本文內燃機缸內動網格模型及其流場計算的正確與否，先后設計了以下的動態層網格模型流場算例和匹配的任意邊界網格模型流場算例，并將計算結果與商業軟件的計算結果進行了對比。

3.1 動態層網格模型驗證

1)測試算例

任意選取了一個氣缸模型，活塞的半徑為0.017m，沖程為0.05m，曲軸轉速為1 000r/min，回轉半徑為0.024 75m，連桿長度為0.1m。計算的壓力初值為100 000Pa，溫度初值為300K。采用六面體網格單元，共劃分了550個網格，初始網格模型如圖3所示，計算時間為180°BTDC到180°ATDC，計算得到的平均壓力和溫度曲線如圖4所示。

由圖4可知，計算所得的缸內平均壓力和平均溫度曲線與商業軟件PUMPLINX計算所得結果幾乎完全吻合。

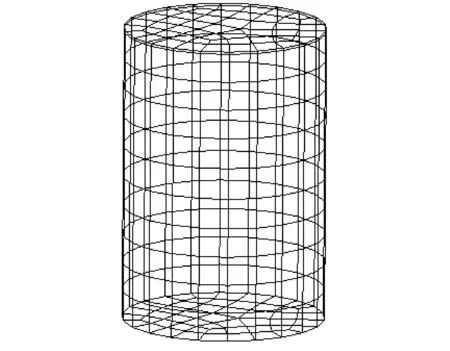
圖3 測試算例網格模型Fig.3 Grid model of test case

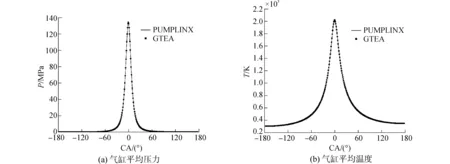
圖4 氣缸平均壓力、溫度曲線對比Fig.4 Cylinder mean pressure and mean temperature curve comparison

圖5 TBD620內燃機氣缸模型Fig.5 Internal combustion engine cylinder model of TBD620

2)TBD620氣缸算例

TBD620內燃機活塞的半徑為0.085m，沖程為0.2m；曲軸轉速為1 800r/min，回轉半徑為0.097 5m，連桿長度為0.35m。計算的壓力初值為30 000Pa，溫度初值為380K。采用六面體網格單元，共劃分了25 752個網格。初始缸內計算域網格模型如圖5所示，計算得到的平均壓力和溫度曲線如圖6所示。

由圖6可知，計算所得的缸內壓力和溫度曲線與商業軟件FLUENT的計算所得結果幾乎完全吻合。

3.2 燃燒室流場仿真驗證

為了模擬完整的缸內過程流場仿真，還要加上燃燒室部分，建立的TBD620完整的缸內燃燒室模型如圖7所示，氣缸部分為六面體網格，燃燒室部分為金字塔和四面體混合單元，結合面處為一一對應的四邊形面單元，網格數為10 786。

如圖8所示為缸內壓縮和膨脹過程所得到的壓力和溫度曲線與FLUENT計算結果對比圖，可看出結果還是基本完全重合，說明了任意邊界網格模型與流場耦合正確。

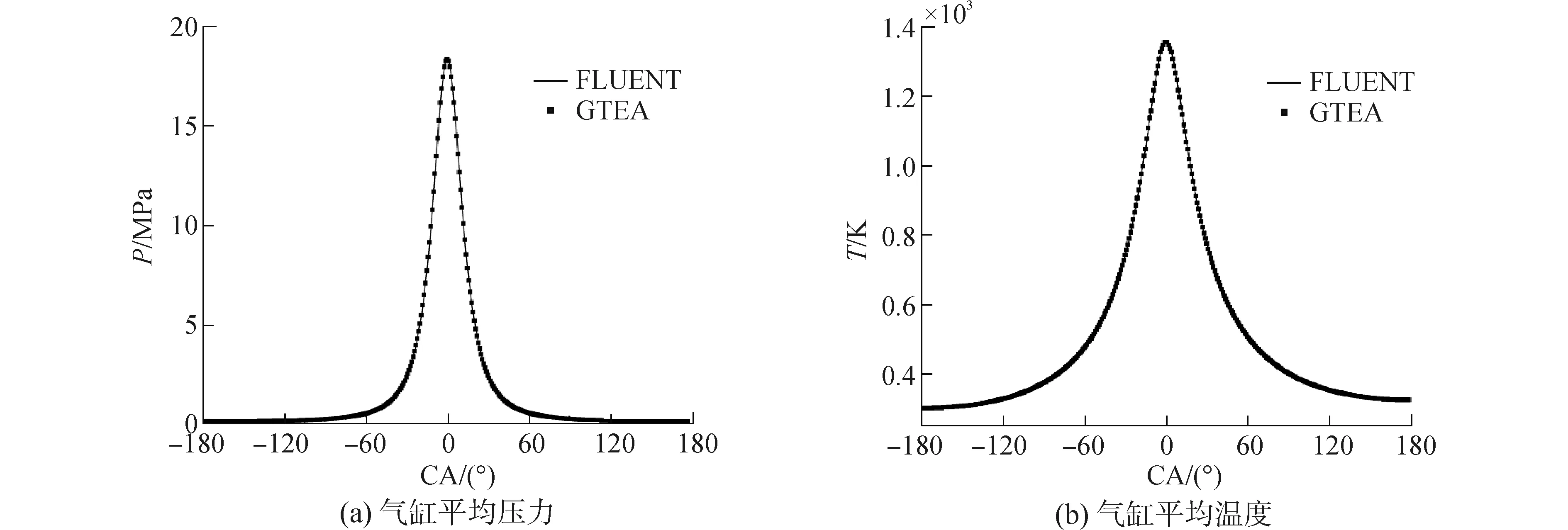
圖6 氣缸平均壓力、溫度曲線對比Fig.6 Cylinder mean pressure and mean temperature curve comparison of TBD620

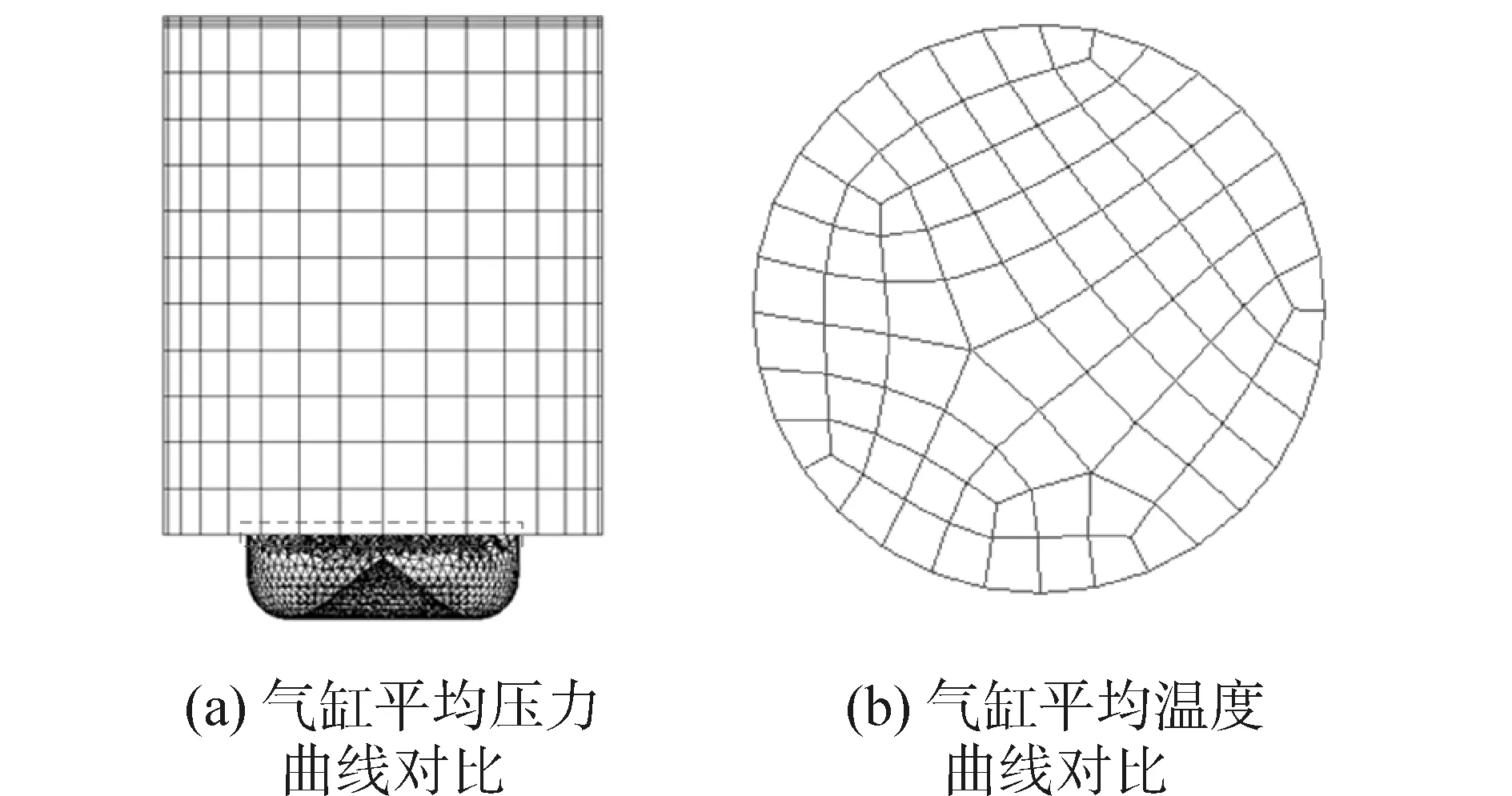
圖7 TBD620內燃機氣缸Fig.7 Complete model of engine of TBD620

如圖9所示為10°BTDC和10°ATDC時的氣缸縱截面矢量圖和全域速度矢量圖的仰視圖，可以發現活塞在上行到上止點之前，四周的氣體流向燃燒室，會在燃燒室的兩個凹坑內形成非常明顯滾流漩渦，同理當活塞下行到上止點后，燃燒室內的氣體由流出到活塞定于氣缸蓋的空間，會在燃燒室凹坑內形成兩個逆向的滾流漩渦，可見這種氣體流動形式可以使燃料與空氣混合完全，符合柴油機工作時的實際情況有利于燃料燃燒。

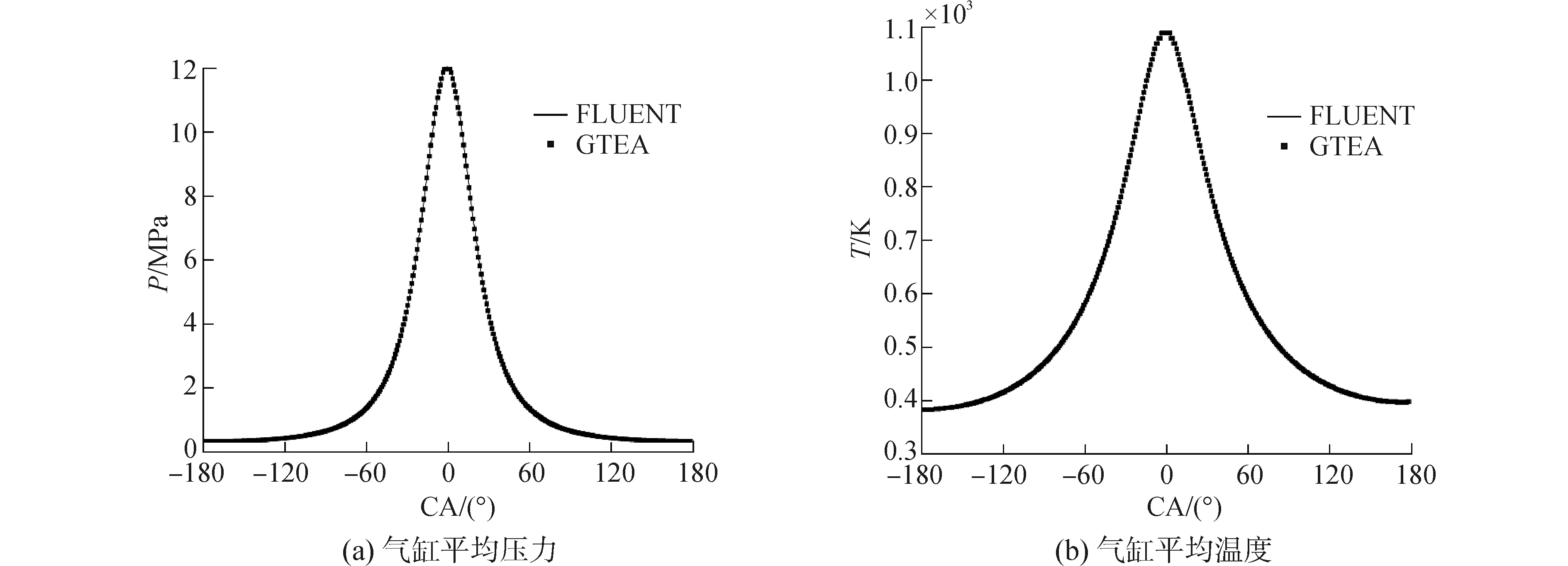
圖8 氣缸平均壓力、溫度曲線對比Fig.8 Cylinder mean pressure and mean temperature curve comparison of TBD620

圖9 流場速度矢量圖Fig.9 Flow velocity vector diagram

4 結論

本文在動態層網格模型和任意邊界網格模型的基礎上，采用有限體積法離散流場控制方程，SIMPLEC算法求解NS方程，開發了一套三維缸內動網格流場數值模擬程序，即自主程序GTEA。并利用氣缸算例和燃燒室算例進行驗證，將GTEA仿真模擬所得的缸內平均壓力值和缸內平均溫度值與商業軟件PUMPLINX和FLUENT計算結果對比，發現本文所得的缸內曲線與商業軟件所得結果幾乎完全吻合，并且給出了TBD620柴油機的缸內流場速度矢量圖，就目前來講，本自主程序可為相關仿真研究提供一定的指導和參考意義。

[1]舒歌群, 馬維忍, 許世杰, 等. 噴霧夾角對柴油機性能影響的數值模擬[J]. 工程熱物理學報, 2008, 29(7): 1239-1242. SHU Gequn, MA Weiren, XU Shijie, et al. Simulation of the effect of spray angle on diesel performance[J]. Journal of engineering thermophysics, 2008, 29(7): 1239-1242.

[2]AMSDEN A A, O'ROURKE P J, BUTLER T D. KIVA-II: a computer program for chemically reactive flows with sprays[R]. Technical Report LA-11560-MS. Los Alamos, New Mexico: Los Alamos National Laboratory, 1989.

[3]明平劍. 基于非結構化網格氣液兩相流數值方法及并行計算研究與軟件開發[D]. 哈爾濱: 哈爾濱工程大學, 2008. MING Pingjian. Development of numerical modeling for gas-liquid two-phase flows based on unstructured grids and parallel computing[D]. Harbin: Harbin Engineering University, 2008.

[4]雷國東. 非結構網格FVM在復雜幾何結構的湍流反應流計算中的應用研究[D]. 哈爾濱: 哈爾濱工程大學, 2008. LEI Guodong. The application and research of the unstructured grid FVM in the turbulent reaction flows simulation with complex geometries[D]. Harbin: Harbin Engineering University, 2008.

[5]張志榮, 冉景煜, 張力, 等. 內燃機缸內氣體CFD瞬態分析中動態網格劃分技術[J]. 重慶大學學報: 自然科學版, 2005, 28(11): 97-100, 121. ZHANG Zhirong, RAN Jingyu, ZHANG Li, et al. Techniques of dynamic mesh in the CFD transient analysis of an engine[J]. Journal of Chongqing university: natural science edition, 2005, 28(11): 97-100, 121.

[6]孫華文. 基于非結構動網格的內燃機瞬態流場仿真[D]. 哈爾濱: 哈爾濱工程大學, 2014. SUN Huawen. Numerical simulation of the transient flow in diesel engine based on unstructured dynamic meshes[D]. Harbin: Harbin Engineering University, 2014.

[7]PATANKAR S V, SPALDING D B. A calculation procedure for heat, mass and momentum transfer in three-dimensional parabolic flows[J]. International journal of heat and mass transfer, 1972, 15(10): 1787-1806.

[8]劉永豐. 基于非結構網格的缸內兩相反應流數值模擬方法研究及軟件開發[D]. 哈爾濱: 哈爾濱工程大學, 2013. LIU Yongfeng. Development of numerical simulation for the process of two phases reacting flow in cylinder based on unstructured grids[D]. Harbin: Harbin Engineering University, 2013.

[9]RHIE C M, CHOW W L. Numerical study of the turbulent flow past an airfoil with trailing edge separation[J]. AIAA journal, 1983, 21(11): 1525-1532.

[10]王福軍. 計算流體動力學分析-CFD軟件原理與應用[M]. 北京: 清華大學出版社, 2004: 1-2, 25-28. WANG Fujun. Computational fluid dynamics analysis-theory and application of CFD software[M]. Beijing: Tsinghua University Press, 2004: 1-2, 25-28.

[11]PERAIRE J, VAHDATI M, MORGAN K, et al. Adaptive remeshing for compressible flow computations[J]. Journal of computational physics, 1987, 72(2): 449-466.

[12]BATINA J T. Unsteady Euler airfoil solutions using unstructured dynamic meshes[J]. AIAA journal, 1990, 28(8): 1381-1388.

Development of numerical simulation program for 3D moving grid and flow field in the cylinder of a diesel engine

LIU Xiaogang, MING Pingjian, ZHANG Gejian, ZHANG Wenping

(College of Power and Energy Engineering, Harbin Engineering University, Harbin 150001, China)

As mature CFD simulation software is currently developed overseas and domestic companies lack intellectual property rights, to ameliorate this problem, Harbin Engineering University developed a set of simulation programs that, after many years of accumulation, have proven to be remarkably successful. To continue conducting a numerical simulation of the three-dimensional working process in the cylinder of an internal combustion engine, a dynamic layer model and a matching model with an arbitrary boundary were firstly established. Moreover, the finite volume method was used to discretize the flow field control equations, and the Navier-Stokes equation was solved using the SIMPLEC algorithm. Based on the FORTRAN language, a set of simulation software of the internal flow field inside the cylinder of a diesel engine was then developed. The air compression and expansion process inside the cylinder were subsequently simulated and analyzed. Moreover, results showed that the cylinder pressure curve and cylinder temperature curve agree well with results of commercial software PUMPLINX and FLUENT, testifying that the moving grid model and the flow field simulation method are correct and that the numerical simulation program has potential as a market application.

I.C. Engine; moving grid; CFD; numerical simulation; program development; software simulation

2015-09-08.

日期：2016-10-12.

國家自然科學基金項目(51206031,51479038);國防預研基金項目(034315003).

劉曉剛(1990-)，男，碩士； 明平劍(1980-)，男，副教授，博士生導師.

明平劍, E-mail: pingjianming@hrbeu.edu.cn.

10.11990/jheu.201509023

TK402

A

1006-7043(2016) 11-1485-07

劉曉剛，明平劍，張格健，等. 柴油機缸內三維動網格和流場數值模擬程序開發[J]. 哈爾濱工程大學學報, 2016, 37(11): 1485-1491. LIU Xiaogang, MING Pingjian, ZHANG Gejian, et al. Development of numerical simulation program for 3D moving grid and flow field in the cylinder of a diesel engine[J]. Journal of Harbin Engineering University, 2016, 37(11): 1485-1491.

網絡出版地址：http://www.cnki.net/kcms/detail/23.1390.u.20161012.0927.004.html