一種自適應(yīng)慣性權(quán)重的改進(jìn)磷蝦群算法
郭 偉, 高岳林, 劉 沛
(北方民族大學(xué) 信息與系統(tǒng)科學(xué)研究所,銀川 750021)
?
一種自適應(yīng)慣性權(quán)重的改進(jìn)磷蝦群算法
郭 偉, 高岳林, 劉 沛
(北方民族大學(xué) 信息與系統(tǒng)科學(xué)研究所,銀川 750021)
提出一種自適應(yīng)慣性權(quán)重的磷蝦群算法(AKH)。通過(guò)理論論證,得出在采用線(xiàn)性遞減的磷蝦群算法求解全局優(yōu)化問(wèn)題的迭代過(guò)程中,出現(xiàn)大量無(wú)效迭代是受到慣性權(quán)重的影響;進(jìn)而提出相關(guān)改進(jìn)策略:在以目標(biāo)函數(shù)作為適應(yīng)度值的基礎(chǔ)上,將種群粒子動(dòng)態(tài)分為適應(yīng)度值變差粒子和適應(yīng)度值變優(yōu)粒子兩類(lèi),令適應(yīng)度值變差粒子的慣性權(quán)重重置為零,從而消除慣性權(quán)重對(duì)算法當(dāng)前迭代的不良影響,適應(yīng)度值變優(yōu)粒子的慣性權(quán)重保持不變;對(duì)算法中的步長(zhǎng)縮放因子作非線(xiàn)性遞減處理,進(jìn)一步提升算法的全局探索能力。通過(guò)9個(gè)具有代表性的測(cè)試函數(shù)進(jìn)行實(shí)驗(yàn),將該算法與線(xiàn)性遞減的粒子群算法(LPSO)、標(biāo)準(zhǔn)磷蝦群算法(KH)和線(xiàn)性遞減的磷蝦群算法(LKH)作性能對(duì)比分析。實(shí)驗(yàn)表明,該算法能夠有效地減少無(wú)效迭代次數(shù),在全局探索性能和收斂穩(wěn)定性方面有著顯著優(yōu)勢(shì)。
磷蝦群算法;全局優(yōu)化;自適應(yīng);慣性權(quán)重
智能優(yōu)化算法是一種以數(shù)學(xué)為基礎(chǔ),用于解決各種優(yōu)化問(wèn)題的算法。磷蝦群算法(KH)[1]是一種新的群智能優(yōu)化算法,該算法是基于對(duì)南極磷蝦的生存環(huán)境及生活習(xí)性的仿真模擬[2],由GANDOMI et al在2012年首次提出。在海洋中存在著捕食者,南極磷蝦群為了更好地存活下來(lái),在運(yùn)動(dòng)過(guò)程中,它們不斷地聚集以增大種群密度減少被捕食的幾率,同時(shí)探索生存區(qū)域,盡可能縮短它們與食物的距離,最終使得種群獲取食物。
一般地,與其它智能優(yōu)化算法相比,標(biāo)準(zhǔn)磷蝦群具有自身良好特性,在解決一些復(fù)雜優(yōu)化問(wèn)題[3-5]時(shí)具有極強(qiáng)的收斂能力,然而,由于在算法迭代過(guò)程中粒子運(yùn)動(dòng)的隨機(jī)性,在算法運(yùn)行時(shí),當(dāng)粒子運(yùn)動(dòng)到適應(yīng)度值較差位置時(shí),并未對(duì)粒子的運(yùn)動(dòng)狀態(tài)進(jìn)行適時(shí)調(diào)整,從而出現(xiàn)大量的無(wú)效迭代,使得算法并非總能很好地完成全局搜索,特別是在處理一些多峰優(yōu)化問(wèn)題時(shí),算法的解更易陷入局部最優(yōu),出現(xiàn)“早熟”現(xiàn)象。對(duì)此,研究人員對(duì)標(biāo)準(zhǔn)磷蝦群算法從不同方面對(duì)算法進(jìn)行改進(jìn),文獻(xiàn)[6-8]主要通過(guò)對(duì)算法中的部分參數(shù)進(jìn)行調(diào)整,從而提升算法的搜索性能。
筆者提出了一種自適應(yīng)慣性權(quán)重的磷蝦群算法(AKH),在磷蝦群算法的每一輪迭代中,通過(guò)監(jiān)測(cè)磷蝦群粒子的運(yùn)動(dòng)狀態(tài)來(lái)動(dòng)態(tài)調(diào)整各粒子的慣性權(quán)重,消除迭代過(guò)程中慣性權(quán)重的不良影響,減少算法的無(wú)效迭代次數(shù),使得磷蝦群算法能夠更好地進(jìn)行全局探索,同時(shí)收斂穩(wěn)定性得到明顯提升。
1 標(biāo)準(zhǔn)磷蝦群算法
磷蝦群算法是一種新的啟發(fā)式智能優(yōu)化算法,該算法主要基于對(duì)南極磷蝦群在海洋環(huán)境中的運(yùn)動(dòng)過(guò)程的仿真研究。對(duì)于每個(gè)磷蝦粒子,它的位置更新主要受到三個(gè)因素的影響:
1) 周?chē)孜r的誘導(dǎo);
2) 覓食活動(dòng);
3) 隨機(jī)擴(kuò)散。
磷蝦粒子的速度更新公式采用了以下的拉格朗日模型:
(1)
式中,Ni,Fi,Di分別代表第i個(gè)粒子運(yùn)動(dòng)速度受到上面所提三個(gè)因素的影響。
三個(gè)因素的公式構(gòu)造如下:
(2)
(3)
(4)
式中:Nmax,Vf,Dmax分別代表最大誘導(dǎo)速度、最大覓食速度和最大擴(kuò)散速度;αi,βi,δi分別代表誘導(dǎo)方向、覓食方向和擴(kuò)散方向;wn,wf為慣性參數(shù);t,tmax分別為當(dāng)前迭代次數(shù)和最大迭代次數(shù)。
磷蝦群粒子在t到t+Δt區(qū)間的位置更新公式如下:
(5)
(6)
式中:Δt為速度向量的縮放因子;Ct為步長(zhǎng)縮放因子,取介于[0,2]的常數(shù);NV代表變量數(shù);BU,j,BL,j分別為第j個(gè)變量的上界和下界。
為了進(jìn)一步提升算法的性能,在算法中執(zhí)行遺傳算子(交叉或變異),經(jīng)測(cè)試,交叉算子更為有效[1]。
(7)
(8)
式(5)中,Δt是一個(gè)重要的變量,文獻(xiàn)[8]對(duì)式(6)中的Ct采用式(9)進(jìn)行處理,將該算法記為L(zhǎng)KH。
(9)
標(biāo)準(zhǔn)磷蝦群算法的流程:
Step 1 種群初始化及參數(shù)設(shè)置,包括當(dāng)前迭代次數(shù)t=1,初始種群粒子位置xi(t),種群規(guī)模NP,最大迭代次數(shù)tmax,最大誘導(dǎo)速度Nmax,最大覓食速度Vf,最大隨機(jī)擴(kuò)散速度Dmax,誘導(dǎo)慣性權(quán)重wn,覓食慣性權(quán)重wf和步長(zhǎng)縮放因子Ct等。
Step 2 將目標(biāo)函數(shù)值作為適應(yīng)度值,評(píng)價(jià)每個(gè)粒子的適應(yīng)度。
Step 3 利用式(2)-式(4)分別對(duì)磷蝦群粒子運(yùn)動(dòng)的速度分量計(jì)算:a.誘導(dǎo)速度Ni;b.覓食速度Fi;c.隨機(jī)擴(kuò)散速度Di.
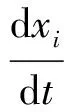
Step 5 根據(jù)式(7)或式(8)對(duì)粒子進(jìn)行遺傳操作(一般采用交叉操作)以增加種群的多樣性。
Step 6 計(jì)算迭代后種群粒子的適應(yīng)度值,對(duì)粒子的位置進(jìn)行更新。
Step 7 令t=t+1,返回Step 3,直到滿(mǎn)足t達(dá)到設(shè)定的最大迭代次數(shù)tmax.
2 算法問(wèn)題分析
由仿真試驗(yàn)可知,在采用KH和LKH算法求解復(fù)雜的非線(xiàn)性全局優(yōu)化問(wèn)題時(shí),算法迭代過(guò)程中存在著大量的無(wú)效迭代。圖1給出了采用KH和LKH算法對(duì)F1(D=30)的一次仿真試驗(yàn)。
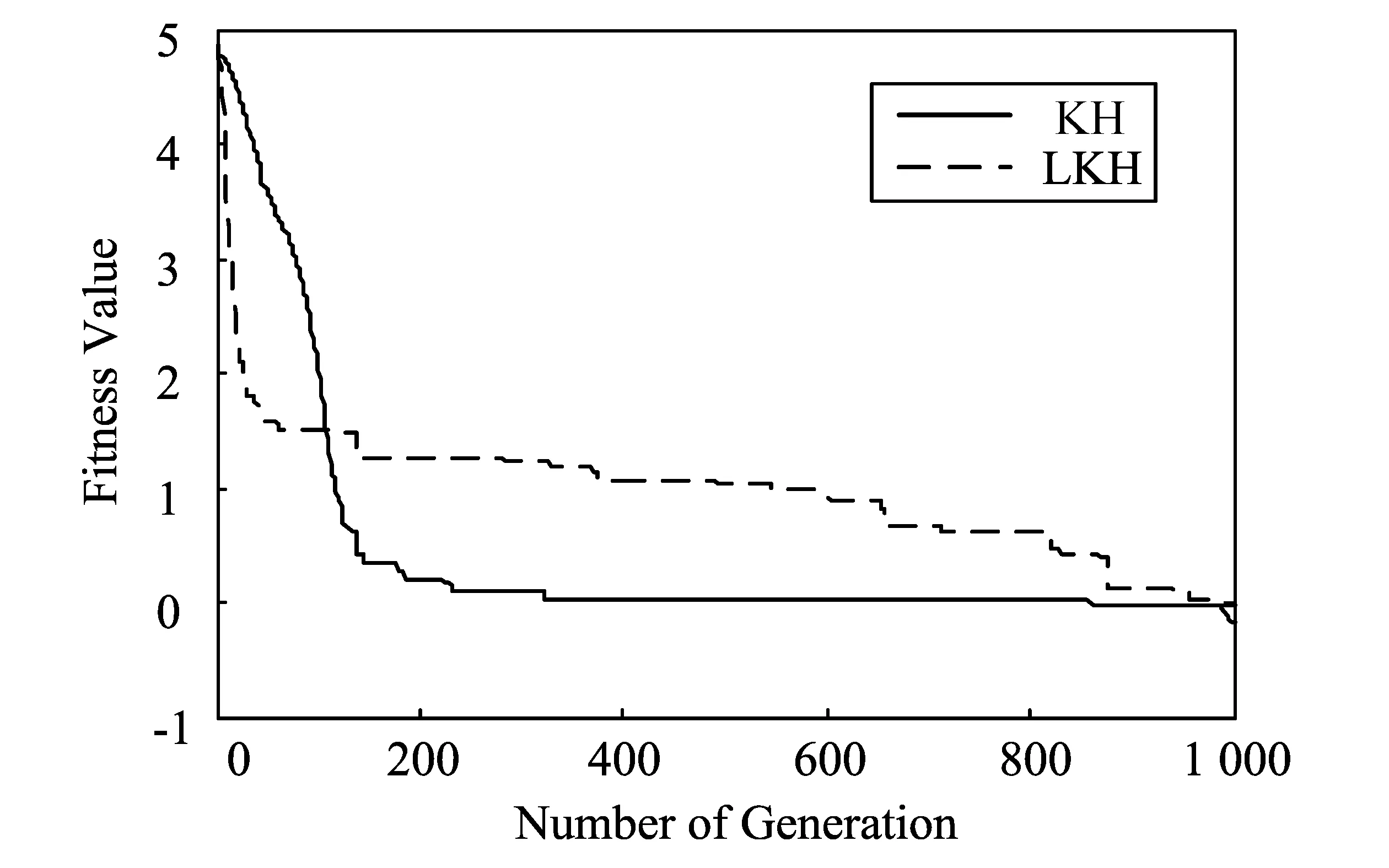
圖1 KH和LKH算法對(duì)F1(D=30)的仿真試驗(yàn)Fig.1 The experiment of KH and LKH for F1
在問(wèn)題求解的迭代前期,算法具有良好的的收斂速度,但是,隨著迭代次數(shù)的增加,出現(xiàn)了大量的無(wú)效迭代,使得KH和LKH算法的收斂速度和收斂精度受到嚴(yán)重影響。
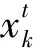
(10)
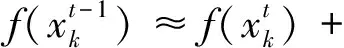
(11)
將式(5)代入式(10)化簡(jiǎn),得
(12)
當(dāng)粒子在上一輪迭代到適應(yīng)度值更差位置時(shí),即
(13)
又,Δt>0,由式(1)、式(12)和式(13)得
(14)
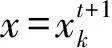
(15)
3 自適應(yīng)慣性權(quán)重的磷蝦群算法
3.1 改進(jìn)方案
基于上述分析,筆者對(duì)磷蝦群算法提出了一種簡(jiǎn)單的改進(jìn)方案。在迭代過(guò)程中,根據(jù)粒子適應(yīng)度值的變化,將粒子分成兩類(lèi):適應(yīng)度值變差的粒子和適應(yīng)度值變優(yōu)的粒子。對(duì)于適應(yīng)度值變差的粒子,令其下一次迭代的慣性權(quán)重wn=0,wf=0;對(duì)于適應(yīng)度值變優(yōu)的粒子,令其下一次迭代的慣性權(quán)重保持不變。
(16)
(17)
同時(shí),采式(18)處理步長(zhǎng)縮放因子Ct,相較于式(9)的線(xiàn)性遞減,非線(xiàn)性操作可以提升Ct的下降趨勢(shì),在算法迭代的過(guò)程中,保證了在前期可以獲得更大的探索范圍,后期加快粒子的收斂速度。
(18)
3.2 算法流程
Step 1 種群初始化及參數(shù)設(shè)置,包括當(dāng)前迭代次數(shù)t=1,初始種群粒子位置xi(t),種群規(guī)模NP,最大迭代次數(shù)tmax,最大誘導(dǎo)速度Nmax,最大覓食速度Vf,最大隨機(jī)擴(kuò)散速度Dmax,誘導(dǎo)慣性權(quán)重wn,覓食慣性權(quán)重wf和步長(zhǎng)縮放因子Ct等。
Step 2 將目標(biāo)函數(shù)值作為適應(yīng)度值,評(píng)價(jià)每個(gè)粒子的適應(yīng)度。
Step 3 利用式(2)-(4)分別對(duì)磷蝦群粒子運(yùn)動(dòng)的速度分量計(jì)算:a.誘導(dǎo)速度Ni;b.覓食速度Fi;c.隨機(jī)擴(kuò)散速度Di.
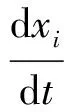
Step 5 根據(jù)式(7)或式(8)對(duì)粒子進(jìn)行遺傳操作(一般采用交叉操作)以增加種群的多樣性。
Step 6 計(jì)算迭代后種群粒子的適應(yīng)度值,根據(jù)適應(yīng)度值對(duì)粒子的位置進(jìn)行更新替換。
Step 7 通過(guò)比較當(dāng)前代粒子適應(yīng)度值的變化,采用式(16)、式(17)動(dòng)態(tài)調(diào)整粒子慣性權(quán)重;
Step 8 令t=t+1,返回Step 3,直到滿(mǎn)足t達(dá)到設(shè)定的最大迭代次數(shù)tmax.
具體流程圖如圖2所示。
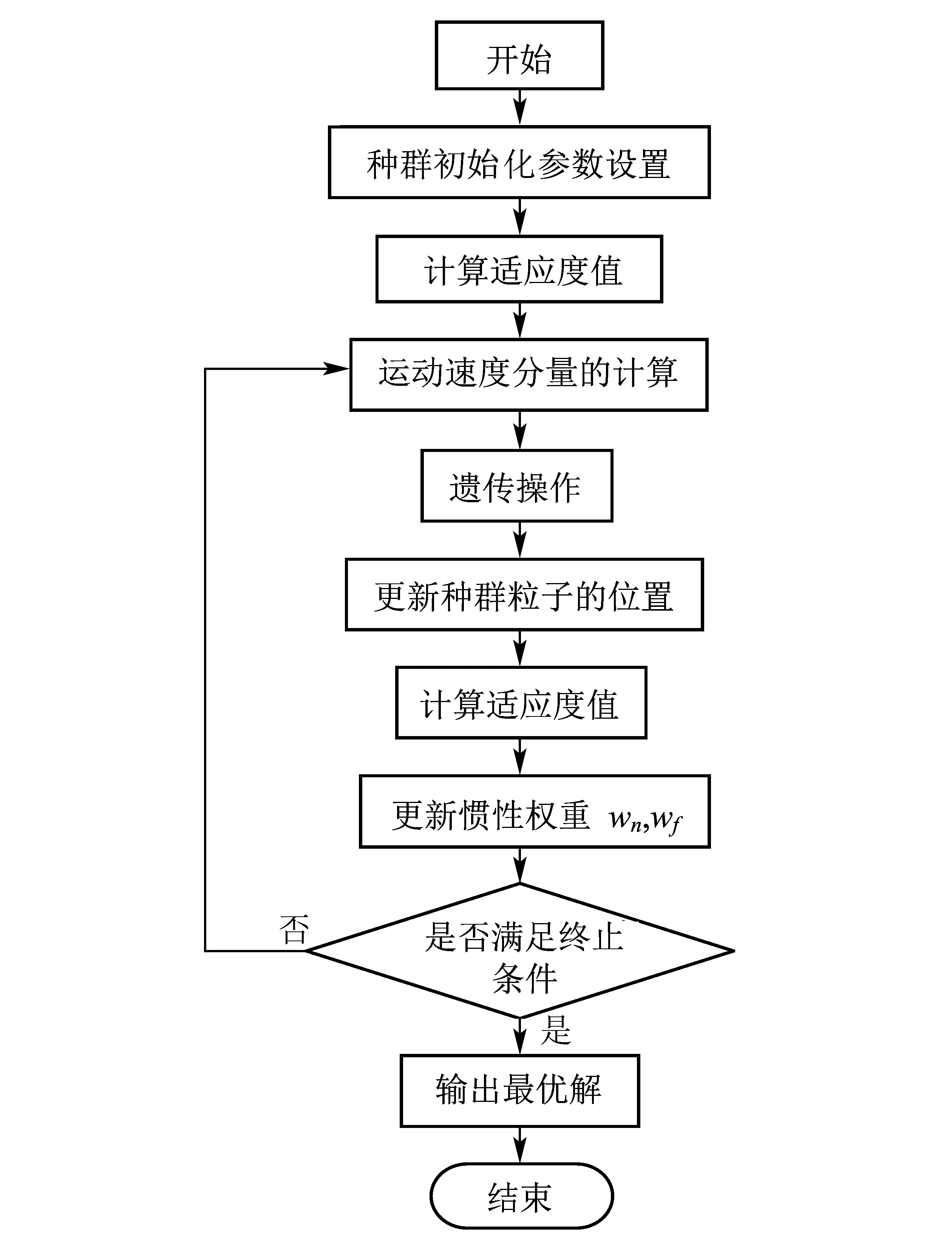
圖2 AKH流程圖Fig.2 The flow chart of AKH
4 對(duì)比實(shí)驗(yàn)
4.1 實(shí)驗(yàn)說(shuō)明
實(shí)驗(yàn)操作環(huán)境:運(yùn)行軟件—Matlab2012a;電腦配置—Intel(r)Core(TM)i5-4440CPU@3.10GHz,8.00GB.
實(shí)驗(yàn)測(cè)試指標(biāo):對(duì)于搜索類(lèi)算法的收斂性能評(píng)估,一般可以分為算法的求解效率和求解質(zhì)量?jī)煞矫?本文從求解質(zhì)量的角度來(lái)考慮算法的收斂有效性,求解質(zhì)量是指在規(guī)定的迭代次數(shù)(或時(shí)間內(nèi))所獲得可行解的優(yōu)劣。
當(dāng)算法進(jìn)化的終止目標(biāo)是達(dá)到最大迭代次數(shù)時(shí),主要有兩個(gè)評(píng)價(jià)指標(biāo):平均最優(yōu)適應(yīng)度值和標(biāo)準(zhǔn)方差。
1) 平均最優(yōu)適應(yīng)度值。達(dá)到最大迭代次數(shù)時(shí),所得到最優(yōu)解的平均值。平均適應(yīng)度值越接近于全局最優(yōu)解,表明算法的尋優(yōu)性能越好。對(duì)于最小優(yōu)化問(wèn)題,解的平均適應(yīng)度越小越好。
2) 標(biāo)準(zhǔn)方差。達(dá)到最大迭代次數(shù)時(shí)優(yōu)化算法所得到的最優(yōu)解的標(biāo)準(zhǔn)方差。該指標(biāo)反映了算法的穩(wěn)定性。對(duì)于穩(wěn)定的算法而言,其每次優(yōu)化所得結(jié)果之間差異很小。算法的質(zhì)量平均最有適應(yīng)度值和標(biāo)準(zhǔn)方差共同反映。
同時(shí),在測(cè)試結(jié)果中給出了最小值和最大值,二者體現(xiàn)算法在規(guī)定的最大迭代次數(shù)內(nèi)所能探索到的最好的可行解,二者越小,進(jìn)一步表明算法的求解質(zhì)量越高。對(duì)于磷蝦群算法,在文獻(xiàn)[1]中的測(cè)試函數(shù)在1 000次迭代結(jié)果就能達(dá)到一定的求解精度,在此,本文中的實(shí)驗(yàn)每次獨(dú)立運(yùn)行最大迭代次數(shù)設(shè)為1 000次。
為了驗(yàn)證本文所提出算法AKH的有效性,將算法與KH(標(biāo)準(zhǔn)磷蝦群算法)、LKH(變量Ct線(xiàn)性遞減)分別對(duì)表1中的9個(gè)Benchmark優(yōu)化問(wèn)題[11]進(jìn)行性能對(duì)比實(shí)驗(yàn),同時(shí),為了進(jìn)一步體現(xiàn)磷蝦群算法的快速收斂性,將算法與LPSO(變量w線(xiàn)性遞減)進(jìn)行對(duì)比實(shí)驗(yàn)。
表中,f1是典型的單峰函數(shù),在解的搜索空間中僅有一個(gè)極值點(diǎn);f2為病態(tài)函數(shù),是一個(gè)經(jīng)典復(fù)雜優(yōu)化問(wèn)題,它的全局最優(yōu)點(diǎn)位于一個(gè)平滑、狹長(zhǎng)的拋物形山谷內(nèi)。由于函數(shù)僅僅為優(yōu)化算法提供了少量信息,使得算法很難辨別搜索方向,找到全局最優(yōu)點(diǎn)的機(jī)會(huì)微乎其微,f3在搜索空間中為不連續(xù)、不可微的單峰函數(shù)。f4-f9是典型的非線(xiàn)性多峰函數(shù),在搜索空間中存在大量的局部極值點(diǎn)。所有實(shí)驗(yàn)的種群規(guī)模均為50,每個(gè)函數(shù)獨(dú)立運(yùn)行20次,最大迭代次數(shù)設(shè)定為1 000次,
對(duì)于LPSO,c1=c2=2,wmax=0.95,wmin=0.4;
對(duì)于KH,wn=0.7,wf=0.7,Ct=0.4;
對(duì)于LKH和AKH,wn=0.7,wf=0.7,Ct,max=1.9,Ct,min=0.1 .
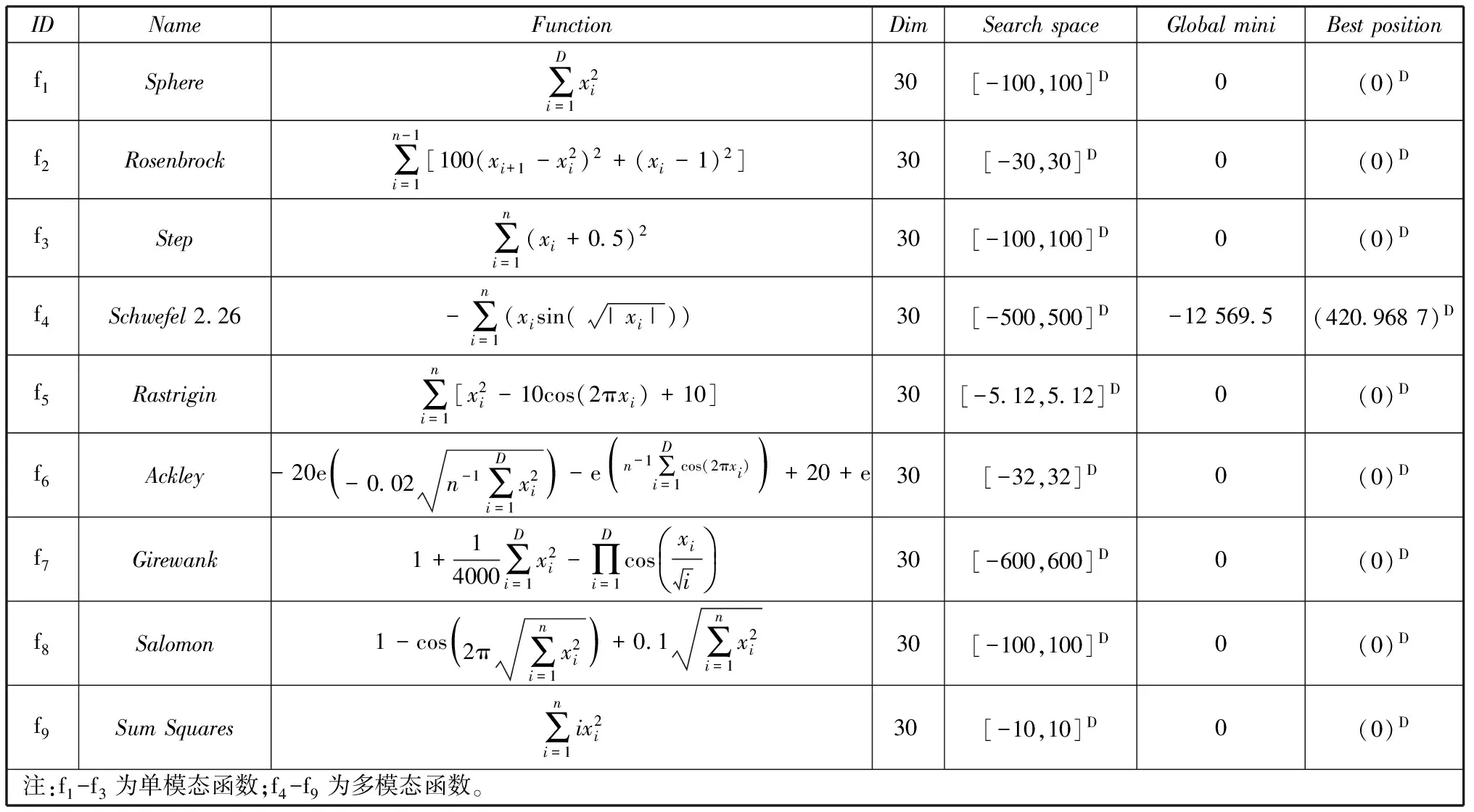
表1 Benchmark函數(shù)
4.2 Benchmark問(wèn)題對(duì)比實(shí)驗(yàn)結(jié)果分析
首先,由測(cè)試函數(shù)對(duì)比試驗(yàn)圖可以看出,對(duì)于同樣的測(cè)試函數(shù),在規(guī)定的最大迭代次數(shù)內(nèi),KH、LKH和AKH比LPSO的求解結(jié)果更快地達(dá)到更小的數(shù)量級(jí),這說(shuō)明在一般情況下,磷蝦群算法比粒子群算法具有更強(qiáng)的收斂性和有效性。
圖3(a)和圖3(b)為單峰函數(shù)測(cè)試對(duì)比實(shí)驗(yàn)圖,由圖可以看出,對(duì)于單峰函數(shù),由于大量無(wú)效迭代的
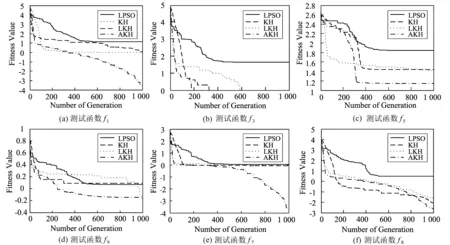
圖3 測(cè)試函數(shù)對(duì)比實(shí)驗(yàn)圖Fig.3 The contrast experiment of test functions
減少,AKH可以更加有效地探尋搜索空間,從而比KH和LKH具有更強(qiáng)的收斂速度和探索能力,進(jìn)一步提升了解的精度。
圖3(c)是多峰函數(shù)Rastrigin的對(duì)比實(shí)驗(yàn)圖,在收斂速度方面AKH介于KH和LKH之間,但是在探索能力方面,AKH強(qiáng)于KH和LKH。圖3(d)是Ackley函數(shù)的對(duì)比實(shí)驗(yàn)圖,在探索能力方面,AKH強(qiáng)于KH,稍弱于LKH,同時(shí),收斂速度弱于LKH,AKH。由圖3(e)和圖3(f)可以看出,相比于其它算法,在迭代前期,AKH具有更快的收斂速度,在迭代后期,AKH仍具有極強(qiáng)的探索能力,從而在求解質(zhì)量方面有所提高。
表2中的各項(xiàng)數(shù)據(jù)顯示,對(duì)于多峰函數(shù)Ackley,AKH在求解精度方面稍弱于LKH,但是強(qiáng)于KH和LPSO,對(duì)于其它測(cè)試函數(shù),AKH算法在最小值、均值和標(biāo)準(zhǔn)方差等方面明顯優(yōu)于其它3種算法,對(duì)于解決復(fù)雜非線(xiàn)性全局優(yōu)化問(wèn)題,具有顯著優(yōu)于其它3種算法的搜索性能,最優(yōu)解的搜索精度具有顯著提高,同時(shí),標(biāo)準(zhǔn)方差結(jié)果表明數(shù)據(jù)差異性相對(duì)較小,具有良好的魯棒性。
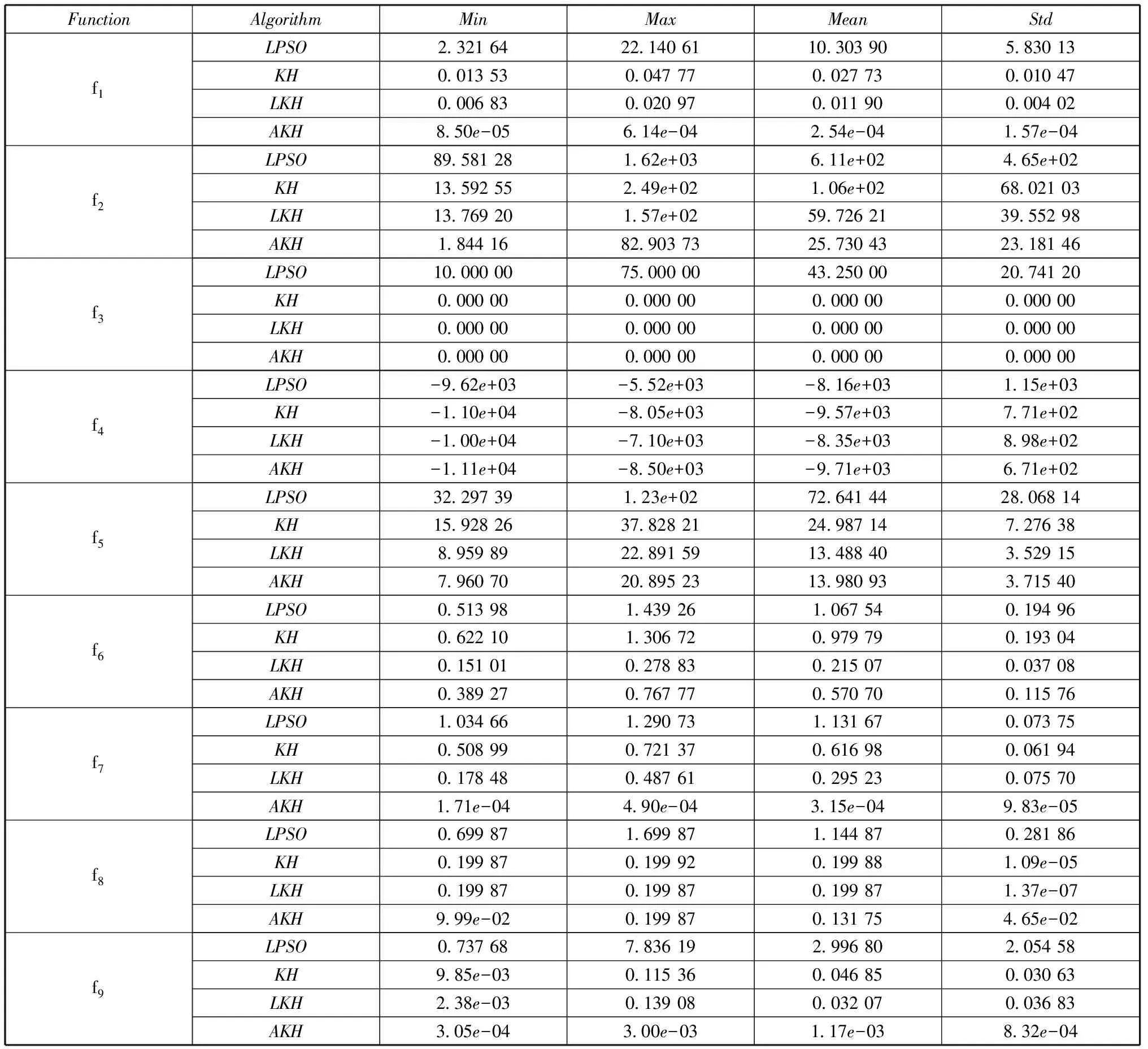
表2 AKH與其它算法在Benchmark問(wèn)題上的數(shù)值對(duì)比
5 結(jié)論
磷蝦群算法具有極強(qiáng)的收斂性能,但是在求解全局優(yōu)化問(wèn)題中,存在大量無(wú)效迭代,而且解易陷入局部最優(yōu)。對(duì)此,為了提升算法的探索能力和收斂性能,本文提出了一種自適應(yīng)慣性權(quán)重的磷蝦群算法,并理論證明了算法改進(jìn)的合理性,通過(guò)對(duì)粒子群體運(yùn)動(dòng)狀態(tài)的分析,動(dòng)態(tài)調(diào)整每一輪迭代中全體粒子的慣性權(quán)重,降低了迭代過(guò)程中慣性權(quán)重的不良影響,從而減少了算法無(wú)效迭代次數(shù)。同時(shí),對(duì)步長(zhǎng)縮放因子進(jìn)行非線(xiàn)性處理,進(jìn)一步提升算法的探索能力,從而提升了解的精度。9個(gè)具有代表性的測(cè)試函數(shù)的數(shù)值實(shí)驗(yàn)對(duì)比表明,本文提出的改進(jìn)算法AKH在探索能力和收斂穩(wěn)定性上顯著優(yōu)于LKH,KH和LPSO。
[1]GANDOMIAH,ALAVIAH.KrillHerd:anewbio-inspiredoptimizationalgorithm,Commun[J].NonlinearSciNumerSimul,2012,17(12):4831-4845.
[2]HOFMANNEE,HASKELLAGE,KLINCKJM,etal.Lagrangianmodellingstudiesofantarctickrill(Euphasiasuperba)swarmformation[J].ICESJMarSci,2004,61:617-31.
[3]MILANT,NEBOJSAB,BRANISLAVP.Krillherd(KH)algorithmappliedtotheconstrainedportfolioselectionproblem[J].Internationaljournalofmathematicsandcomputersinsimulation.Volume,2014,8:1998-0159.
[4]LARINS,ABADEHMS.Trainingartificialneuralnetworkbykrill-herdalgorithm[J].Informationtechnologyandartificialintelligenceconference(ITAIC),2014IEEE7thJointInternational,2014,20/21:63-67.
[5]KOWALSKIPA,LUKASIKS.Tuningneuralnetworkswithkrillherdalgorithm[J].Jointconferencecomputationalintelligence,2014:119-128.
[6]WANGG,GUOL,AMIRHG,etal.Chaotickrillherdalgorithm[J].Informationsciences,2014:0020-0255.
[7]SHAHRZADS,SEYEDMM,SEYEDALIM.Chaotickrillherdoptimizationalgorithm[J].ProcediaTechnology,2014,12:180-185.
[8]LIJP,TANGYG,HUACC,etal.Animprovedkrillherdalgorithm:Krillherdwithlineardecreasingstep[J].Appliedmathematicsandcomputation,2014(234):356-367.
[9]SHIYH,EBERHEARTRC.Parameterselectioninparticleswarmoptimization[C]∥IEEE.7thInternationalConference,EvolutionaryprogrammingVII.BerlinHeidelberg:Springer,1998,1447:591-600.
[10]AOYC,SHIYB,ZHANGW,etal.Improvedparticleswarmoptimizationwithadaptiveinertiaweight[J].JournalofUniversityofElectronicScienceandTechnologyofChina,2014:874-880.
[11]LIANGJ,QUB,SUGANTHANP,etal.ProblemdefinitionsandevaluationcriteriafortheCEC2013specialsessionandcompetitiononreal-parameteroptimization:technicalreport201212[R].Singapo:NanyangTechnologyUniversity,2013.
(編輯:朱 倩)
An Improved Krill Herd Algorithm with Adaptive Inertia Weight
GUO Wei,GAO Yuelin,LIU Pei
(Institute of Information and System Science,Beifang University of Nationalities,Yinchuan 750021,China)
In this paper,an improved krill herd algorithm with adaptive inertia weight is proposed. First, the relationship between the number of invalid iteration and inertia weight in the algorithm is presented, and then the related improvement strategy is put forward.The inertia weights of the particles whose fitness become worse at the last iterations are set to zero while solving the global optimization problems.At the same time, the step length scale factor is decreased nonlinearly.The algorithm can reduce the invalid iterations and enhance global exploring ability. Nine benchmark functions are used to test the AKH, LPSO,KH and LKH. Experiments show that the proposed algorithm can effectively reduce invalid iterations and it has obvious superiority on the search performance and the convergence stability.
krill herd algorithm; global optimization; adaptive;inertia weight
1007-9432(2016)05-0651-07
2015-09-21
國(guó)家自然科學(xué)基金資助項(xiàng)目:基于粒子群優(yōu)化的多目標(biāo)智能算法及應(yīng)用研究(61561001);北方民族大學(xué)重點(diǎn)科研項(xiàng)目資助(2015KJ10);北方民族大學(xué)研究生創(chuàng)新項(xiàng)目:磷蝦群算法的改進(jìn)及應(yīng)用研究(YCX1549)
郭偉(1990-),男,河南信陽(yáng)人,碩士生,主要從事智能計(jì)算與優(yōu)化新技術(shù)研究,(E-mail)864369663@qq.com
高岳林,教授,博士生導(dǎo)師,主要從事智能計(jì)算與智能信息處理,最優(yōu)化理論方法及其應(yīng)用,(E-mail)gaoyuelin@263.net
TP18
A
10.16355/j.cnki.issn1007-9432tyut.2016.05.017

