一元函數極限計算方法綜述
2016-12-15 11:32:09長春建筑學院基礎教學部130607
數理化解題研究 2016年33期
關鍵詞:綜述
長春建筑學院基礎教學部(130607)
付美鑫●
?
一元函數極限計算方法綜述
長春建筑學院基礎教學部(130607)
付美鑫●
在實際生活中,對實際問題的研究,往往是通過函數來實現的,但對于很多求精確解的問題,僅僅通過有限次的算術運算是不能得到的,這就需要考察對于自變量的一個無限變化的過程,函數值具有怎樣的一個變化趨勢,也就產生了極限的思想,本文主要介紹極限的運算方法.
定義 設函數f(x)在點x0的某個去心鄰域內有定義,如果當x趨于x0(或)時,對應的函數值f(x)無限的接近于某個確定的常數A,就說A是函數f(x)當x→x0(或x→)時的極限,記作或f(x)→A(x→x0()).
現對極限的運算方法做如下總結:
一、直接代點法
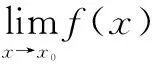
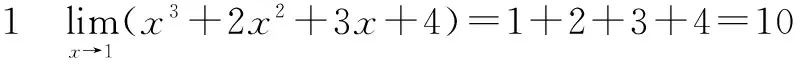
二、有理分式
p(x)=a0xn+a1xn-1+…+an-1x+an,
Q(x)=b0xm+b1xm-1+…+bm-1x+bm,
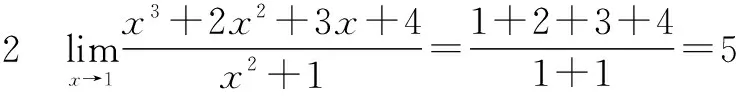
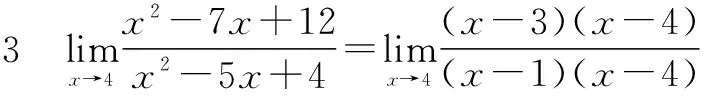
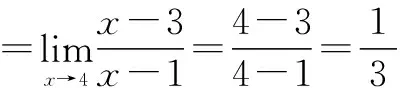
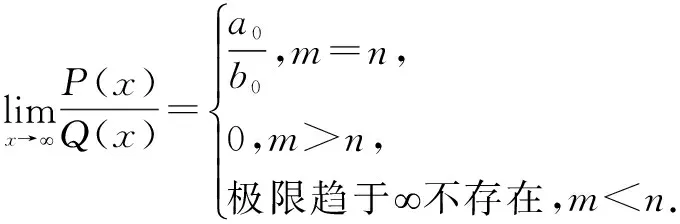
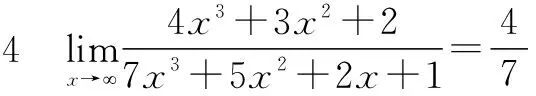
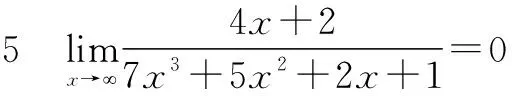
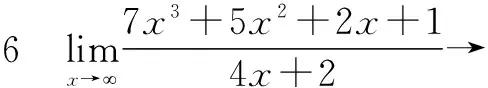
三、分子(分母)有理化法
當分子或分母有根式時,優先考慮分子(分母)有理化法.
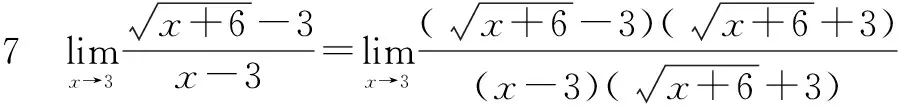
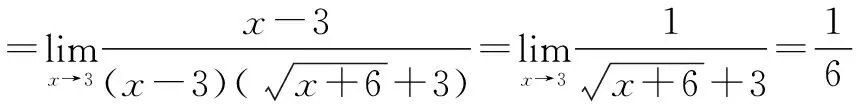
四、利用等價無窮小計算極限
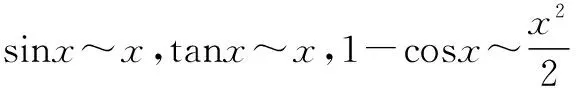
arcsinx~x,arctanx~x,ln(1+x)~x,ex-1~x.
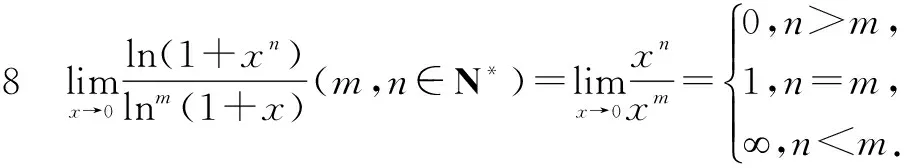
五、夾逼準則
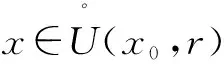
在應用夾逼準則計算極限時,要對函數f(x)做適當的放大和縮小.
六、利用重要極限計算極限
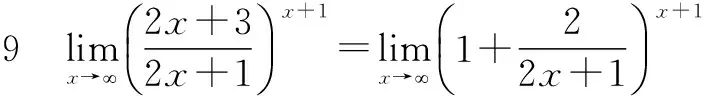
=e=e.
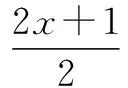
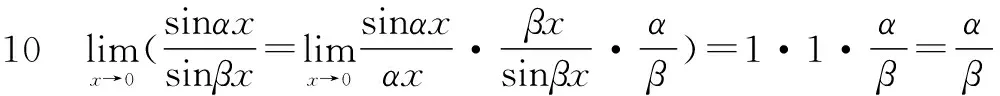
G632
B
1008-0333(2016)33-0002-01
猜你喜歡
話語研究論叢(2022年0期)2022-11-02 09:29:02
文化創新比較研究(2020年8期)2021-01-22 00:38:10
裝備制造技術(2020年2期)2020-12-14 03:09:44
鐵道通信信號(2020年8期)2020-02-06 09:13:18
電子制作(2019年10期)2019-06-17 11:45:16
石油瀝青(2018年6期)2018-12-29 12:07:04
NBA特刊(2018年21期)2018-11-24 02:47:52
自動化學報(2017年11期)2017-04-04 02:52:28
功能高分子學報(2016年1期)2016-04-26 01:39:05
法醫學雜志(2015年2期)2015-04-17 09:58:45

