過程操作:數學教學價值的應然旨歸
江蘇省姜堰中學 (225500)
周 鵬●
?
過程操作:數學教學價值的應然旨歸
江蘇省姜堰中學 (225500)
周 鵬●
注重數學課堂的“過程操作”,對學生的數學學習“過程操作”進行“數學化”的壓縮,將“過程操作”形式化、公理化,引領學生對形式化的抽象數學知識的形成過程進行充分地觀察、描述,逐步地抽象、概括,系統地反思、推理等,實現學生數學思維的提升.
具體;抽象;凝聚;思維;操作
本世紀初,英國數學教育家David Tall在融合了認知主義、結構主義和建構主義等的相關理論后,提出了“數學世界”是數學的“具體化世界”“符號化世界”“形式化世界”的有機交織,認為在學生的學習過程中,他們首先是感性地描述、表征,然后是演繹,進行“邏輯的推理”,最后是提取對象的性質,形成對數學知識的本質認識,產生形式化的定義、公理體系等.在高中數學教學中,我們要立足于學生對數學知識多元化的“心理表征”,對知識形成步驟精致化的“過程操作”和對數學知識簡約化的“抽象凝聚”.在這一系列過程中,要找準數學知識的生發點、生長點、生成點和延伸點.要對數學知識進行“精致化加工”,以讓學生精準化地掌握數學知識.
一、關注多樣化的“心理表征”,凸顯數學知識的本質屬性
學生認知數學知識是在已有的心理圖式上進行的,學習數學知識首先是建立心理表征.在高中數學教學中,幫助學生建立多元的知識心理表征可以擴充數學知識的聯結,增強數學知識的觸發點、延展點.例如高中數學教材中的“函數”概念,學生剛開始學習時同樣需要調動頭腦中相關的表象如“炮彈的軌跡”等進行認知加工,當抽象出函數的表達式后,學生就進入了符號化的加工,最后對函數概念形成本質認識,這時,學生實質上就是進入了函數的形式化世界.再如“等差數列”的概念,在學生通曉生活中常見的等差數列現象之后,筆者讓學生建立起多樣化的心理表征.如建立的文字形式是:從第二項開始的每一項與前一項的差始終是同一個常數;用通項的符號表征是:an-an-1=d(d為常數,n≥2)或者2an=an-1+an+1(n≥2)或者an=kn+b(k、b為常數);用圖形表征就是:建立以(n,an)為坐標的點在一條直線上的表征;或Sn=An2+Bn(A、B是常數),或者建立點(n,Sn)在過原點的拋物線上等.多元化的心理表征凸顯著數學知識的本質屬性,有助于學生對數學知識的理解和完整建構.
二、引領精致化的“過程操作”,讓學生步步數學實踐、創造
數學的“過程操作”主要是讓學生經歷數學知識的形成過程,這個過程伴隨著學生的感知、推理、抽象等的認知活動.數學作為人類“生命·實踐”智慧的結晶,理應讓學生重蹈其中的關鍵步子.在高中數學教學中,如果學生沒有經歷猜想、驗證、判斷、比較、質疑、選擇等的探究過程,沒有自我的分析與綜合等的認知活動,沒有彼此爭論、碰撞等的觀點交流活動,學生就不能深刻理解抽象化的知識.例如“任意角”的概念,教學前首先要分析學生的認知水平,并且對數學教材進行充分地解讀.然后通過實例(如鐘表的旋轉、體操運動員的旋轉、扳手擰動螺絲的旋轉等)引入“任意角”概念.接著引領學生逐層探究:如何定義任意角(旋轉方向和旋轉量);如何設定標準(引入象限角);如何將角放入平面直角坐標系中?終邊相同的角如何用集合表示?通過精致化的“過程操作”,學生對任意角(正角、負角、零角)、象限角、終邊相同角的集合S={β|β=α+k×360,k∈Z}等知識有了精準的掌握.在這個過程中,學生運用了“數形結合”(畫圖操作)思想、類比思想(從數的擴充等現象聯想到角的擴充)、化歸思想(終邊相同的角的集合)、分類思想(k的不同導致角的象限不同)等.在這里,數學超越了機械的“模仿”和純粹的“紙筆訓練”,學生步步進行著數學實踐、數學創造.
三、推進簡約化的“抽象凝聚”,建立相關數學概念間的關聯
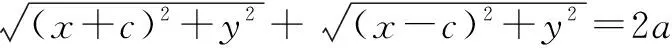
高中數學的學習需要呈現知識的不同層面.數學的“具體化世界”呈現著學生能夠進行數學理解的感性材料,使學生產生了多樣化的心理表征;數學的“符號化世界”讓學生經歷著數學抽象知識的誕生過程,領悟著數學知識生長、生成的關鍵節點;數學的“形式化世界”是對數學知識的必要凝聚、簡約抽象.如此,學生充分地展開著“數學化”活動,提升著思維經驗、方法經驗與思想經驗,學生對數學知識由“工具性理解”導向“關系性理解”,進而實現“創新性理解”.
G632
B
1008-0333(2016)33-0022-01

