倡導(dǎo)合作學(xué)習(xí)，培養(yǎng)學(xué)生數(shù)學(xué)思維品質(zhì)

江蘇省鄭集高級(jí)中學(xué)城區(qū)校區(qū)(221143)

神凌靜●

?

倡導(dǎo)合作學(xué)習(xí)，培養(yǎng)學(xué)生數(shù)學(xué)思維品質(zhì)

江蘇省鄭集高級(jí)中學(xué)城區(qū)校區(qū)(221143)

神凌靜●

本文論述了合作學(xué)習(xí)在數(shù)學(xué)中的作用.

合作學(xué)習(xí)；思維能力；思維品質(zhì)

新課程遵循“以學(xué)生發(fā)展為本”的理念，倡導(dǎo)建立自主、合作、探究的學(xué)習(xí)方式，使學(xué)生真正成為學(xué)習(xí)的主體，體驗(yàn)到學(xué)習(xí)的樂(lè)趣.三大學(xué)習(xí)方式中，合作學(xué)習(xí)起著承前啟后的關(guān)鍵作用.合作學(xué)習(xí)是指學(xué)生在小組或團(tuán)隊(duì)中為了完成共同的任務(wù)，有明確責(zé)任分工的互助性學(xué)習(xí).在合作學(xué)習(xí)的過(guò)程中，不同思維水平的學(xué)生在自主學(xué)習(xí)后，已經(jīng)有過(guò)不同層次的獨(dú)立思考，再通過(guò)生生之間相互溝通、相互啟迪、相互補(bǔ)充，分享彼此的想法、經(jīng)驗(yàn)和知識(shí)，讓思維碰撞，對(duì)提高學(xué)生思維的深刻性、敏捷性、靈活性和創(chuàng)造性等優(yōu)秀思維品質(zhì)作用顯著.

一、在公式教學(xué)中，組織合作學(xué)習(xí)，培養(yǎng)學(xué)生的思維能力

數(shù)學(xué)公式反映了數(shù)學(xué)對(duì)象的屬性之間的關(guān)系，許多數(shù)學(xué)知識(shí)是通過(guò)數(shù)學(xué)公式來(lái)呈現(xiàn)的，數(shù)學(xué)公式的生成過(guò)程即是數(shù)學(xué)知識(shí)的生成過(guò)程.前蘇聯(lián)著名數(shù)學(xué)教育家斯托利亞爾認(rèn)為：數(shù)學(xué)教學(xué)是數(shù)學(xué)活動(dòng)的教學(xué)，也是思維活動(dòng)的教學(xué).

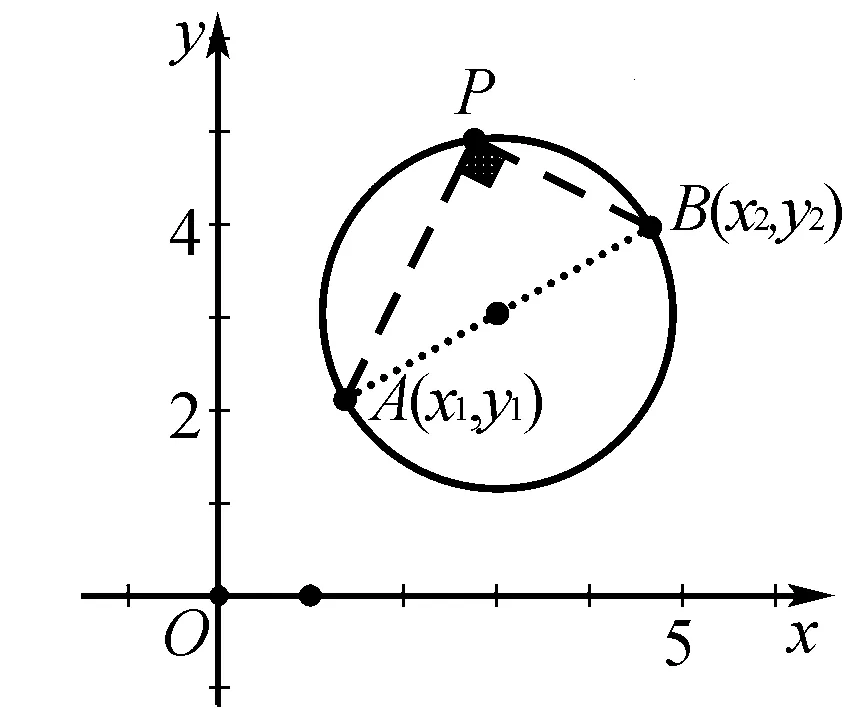
課堂教學(xué)中，老師給出探究題目：已知兩點(diǎn)A(x1,y1)、B(x2,y2).求證：以線段AB為直徑的圓的方程是：(x-x1)(x-x2)+(y-y1)(y-y2)=0.

要求：以學(xué)習(xí)小組為單位，組織研討，嘗試從多個(gè)角度探究證明方法，準(zhǔn)備投影或板演、展示.

學(xué)習(xí)小組內(nèi)充分討論、交流后，組織學(xué)生依次展示出來(lái)，發(fā)現(xiàn)兩種不同的證明方法：

整理，得(x-x1)(x-x2)+(y-y1)(y-y2)=0.

所以x2+y2-(x1+x2)x-(y1+y2)y+x1x2+y1y2=0,可化為(x-x1)(x-x2)+(y-y1)(y-y2)=0.

此后組織學(xué)習(xí)小組間互相點(diǎn)評(píng)，學(xué)生們都很較真，方法一是基本方法，運(yùn)用圓的標(biāo)準(zhǔn)方程，但體會(huì)到化簡(jiǎn)運(yùn)算較繁瑣，有的學(xué)習(xí)小組選擇了跳步，有的學(xué)習(xí)小組代表就對(duì)方法一中的整理過(guò)程提出了質(zhì)疑， 方法二運(yùn)用勾股定理，通過(guò)對(duì)比發(fā)現(xiàn)，方法二較好，思維敏捷，過(guò)程直接、簡(jiǎn)煉.

二、在習(xí)題教學(xué)中，組織合作學(xué)習(xí)，培養(yǎng)學(xué)生的思維能力

平面解析幾何初步中，有一類典型問(wèn)題即對(duì)稱問(wèn)題，分為五種情況：一是點(diǎn)關(guān)于點(diǎn)對(duì)稱，二是點(diǎn)關(guān)于直線對(duì)稱，三是直線關(guān)于直線外一點(diǎn)對(duì)稱，四直線關(guān)于直線對(duì)稱.教學(xué)過(guò)程中，老師給學(xué)生出示一個(gè)題組：

(1)點(diǎn)A(2,3)關(guān)于點(diǎn)B(1,4)的對(duì)稱點(diǎn)A′的坐標(biāo)是____；(2)點(diǎn)A(2,3)關(guān)于直線l:x-y+3=0的對(duì)稱點(diǎn)A′的坐標(biāo)是____；(3)直線l1:x-y+1=0關(guān)于點(diǎn)C(-1,2)的對(duì)稱直線l1′方程是____；(4)直線l1:x-y+1=0關(guān)于直線l:x-y+3=0的對(duì)稱直線方程是____；(5)直線l2:2x-y+1=0關(guān)于直線l:x-y+3=0的對(duì)稱直線方程是____.

要求：按學(xué)習(xí)小組分工負(fù)責(zé)解決各小題：

題號(hào)(1)(2)(3)(4)(5)學(xué)習(xí)小組五三、四六、七一、二八、九

以學(xué)習(xí)小組為單位，組織研討，同一題小組間可以交流，選小組代表投影、展示.

經(jīng)過(guò)研討交流，學(xué)習(xí)小組依次展示出各題的解法：

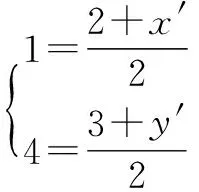
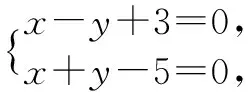
要引導(dǎo)學(xué)生剖析自己發(fā)現(xiàn)和解決問(wèn)題的過(guò)程；學(xué)習(xí)中運(yùn)用了哪些基本的思考方法、技能和技巧，它們的合理性如何，效果如何，有沒(méi)有更好的方法；學(xué)習(xí)中走過(guò)哪些彎路，犯過(guò)哪些錯(cuò)誤，原因何在.

思維品質(zhì)包括思維的深刻性、敏捷性、靈活性、批判性和創(chuàng)造性，它們反映了思維的不同方面的特征.數(shù)學(xué)思維的深刻性品質(zhì)集中體現(xiàn)為學(xué)會(huì)透過(guò)現(xiàn)象看本質(zhì)，學(xué)會(huì)全面地思考問(wèn)題，養(yǎng)成追根究底的習(xí)慣；數(shù)學(xué)思維的敏捷性主要反映了正確前提下的速度問(wèn)題；思維的靈活性，表現(xiàn)為學(xué)生在面臨問(wèn)題時(shí)能夠從多種角度進(jìn)行考慮，并迅速地建立起自己的思路，真正做到舉一反三.

創(chuàng)造性思維品質(zhì)要求在獨(dú)立思考的基礎(chǔ)上，能夠多思善問(wèn)，提出高質(zhì)量的問(wèn)題.提出不同看法并自我鑒別.

批判性思維品質(zhì)的培養(yǎng)，把重點(diǎn)放在引導(dǎo)學(xué)生檢查和調(diào)節(jié)自己的思維活動(dòng)過(guò)程上.

G632

B

1008-0333(2016)28-0049-01