高中生數學思辨習慣養成
南京一中實驗學校(210000)
李紅果 ●
?
高中生數學思辨習慣養成
南京一中實驗學校(210000)
李紅果 ●
思辨對概念教學的作用不可忽視,區別于計算數學的邏輯思維,通過思辨可理解概念,發現問題解法.在數學教學中有計劃地安排學生思辨,對學生的習慣養成起到推動作用.
高中數學;思辨;習慣養成
荷蘭數學家、數學教育家弗賴登塔爾((H.Freudenthal)提出思辨數學的概念,區別于計算數學,也稱思辨數學為概念數學,就是動態地辯證地把握概念和體味推據,憑借對概念的直覺和數學美的啟迪,而產生直觀的解題思路方法或做出合情推理決策.也就是,在直覺的引領下,圍繞推據,換位思考,在運動中找到解題方法的數學知識體系.目前的數學教學,重視計算數學中的邏輯推理,而輕視思辨數學中的直覺思維.思辨數學的作用往往會讓學生的數學思想得到釋放和創新,從而能從直觀上判讀解題思路的可行性,對學生的解題起到決定性的作用,所以數學教師有必要在課堂教學中引領學生思辨習慣的養成.
一、計劃引領,照顧個體
學生的思辨習慣的養成不是一蹴而就,而要有計劃實施,根據課程標準和教材要求編制整體計劃,然后考慮單元計劃、學時計劃等.計劃編制的原則是:一是新課程標準中的思維訓練要求,思辨思維依托于計算思維,重在形成直觀,要與其他思維相輔相成,不可盲目割裂.二是要研究教材中的概念、定理、公式等,對其成因、形成條件、適用范圍、正反推據等都可以通過思辨,搞清概念,定理、公式等才能真正掌握他們,熟于心、達其意,在解題中方能辨別一個個基本問題.三是不能脫離學生實際,學生多會計算思維,高中學生更傾向邏輯思維,基于這兩者的辯證關系,教師引導學生逐步辨析問題的數學模式,靈活使用思辨.四是要小梯度推進,在概念教學中可設置多個小問題,人人皆可參與,人人皆可有觀點,分歧意見可討論,理越辯越明,從而做到清晰概念的效果.
二、分步實施,激勵引導
通過思辨,能讓學生在解題中通過直覺發現解法或數學模型,這是我們的期望.學生數學成績提不高的主要原因是找不到合適的解法,有解法的題通過計算和邏輯推理,自然能夠做好,但沒解法卻是真正讓學生頭疼的事.概念教學來不得馬虎,每一個因素都要辨析和追溯求源,有任何含糊不清的地方都會帶來致命的錯誤.訓練思辨要按計劃分步實施,在小組討論中充分發揮主觀能動性,設置問題開始可有老師提出,以后可有小組提出,甚至可以互相提問,互相答疑.學生需要表揚等激勵,教師要適時給予鼓勵,關注他們的成長,夯實基礎、形成技能,逐步培養與計算思維相當的思辨習慣.
對學生在思維方面的激勵遠比表揚其做好一個題目的效果好的多,對激發學生的學習興趣作用很顯著.激勵辦法可從以下幾方面來做.一是融入小組的激勵機制,納為日常考核指標,對小組與小組間的競爭有一定的推動作用;二是思辨中表現較的同學可以引導其對競賽數學的研究,以表明老師的重視態度,激發其學習數學的動力.三是關注每個學生的表現,找到其思維的亮點,適時表揚,事半功倍.
三、解題訓練、效果為本
直觀往往與圖形相關聯,尤其是學習函數性質、立體幾何、三角函數、解析幾何等內容時.比如指數函數教學
教師給出函數:y=2x、y=1.073x.
師:用字母a表示底數,則上面的式子可表示成y=ax的形式.這就是指數函數.下面請同學們研究討論一下如何給指數函數下個定義.
點評 學生上課是有教材的,教材中對指數函數定義很明白的給出,學生根本就不用思考,只要看一下書就可說出函數概念.學生對底數的認識就不那么清晰了.
建議教師:邊問邊引導學生思辨.
1.對不同的a,對應函數式的值的問題,可分為如下問題思考:①若a<0,能否計算,對應函數是否存在?②若a≠0,函數是否存在?③若a=1,函數將如何?
2.指數函數與冪函數之間是否存在相似之處?是否有關聯?
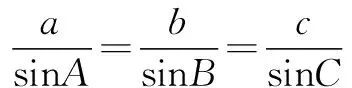
教師:你對這個定理如何理解?
點評 學生不知道從哪入手思考.得到的結論自然有很多偏離問題主題.建議教師:把這個問題設計為多個,然后分組討論研究.(1)各邊與其對角的正弦對應比例,還可以表示成什么形式? (2)如果把定理看成方程,那么這個等式可以看成幾個方程?每個方程中應該已知幾個量求幾個量?
動手實驗能增強感官刺激,加深對概念、圖形的形成起到一定的作用.比如平面的基本性質的教學:
實驗:把鉛筆當作直線、白紙當做一個平面.(1)若鉛筆的兩個端點在白紙內,則鉛筆所在直線上各點與白紙所在的平面有什么關系?(2)若鉛筆有一個端點不在白紙所在的平面內,鉛筆表示的直線與白紙表示的平面有什么關系?
引導學生得出:

公理1 如果一條直線上的兩個點在一個平面內,那么這條直線上所有的點都在這個平面內.
點評 作為公理,建議教師先介紹公理,讓后可以做實驗驗證和理解,學生可以得出很多結論,但公理是共同約定的數學理論是建構空間立體幾何的基點.
思辨的培養在圖形中運用最普遍也最直接,通過點、線的移動或變化,可以有不同的結果,運用數學知識也不盡相同,既起到了訓練的效果,也起到了對相關問題的理解,從而吃透問題的本質,建構所要研究的對象的蘊含關系.
四、變式訓練,遷移創新
對問題的理解、方法的掌握可以通過對條件和結論的思辨做到更深的挖掘.常見的一題多解也是對學生的直觀思維的考查,不同的學生對問題的理解程度不同會對問題的解決方法有不同的直覺,往往會產生不同的解法.同樣地,同一個問題我們可以對條件進行放大或限制、結論的延伸和遷移,可以做到對學生的思辨訓練.從近些年的高考來看,遷移創新問題也占有相當高的比例,新概念、新運算、新規則的問題也很多,解決此類問題主要靠課內的基礎知識、基本技能、定理、原理等的理解,聯想類比靠的是直觀和平時的思辨積累.
思辨習慣的養成來自有計劃的培養,不脫離計算思維,有疑有問,有思有辯,是夯實雙基的必要條件.抓住問題的關鍵,對其產生與概念相關的直覺,通過逆向思維和發散思維,借助類比聯想或換位思考,查找問題的各種關聯,建立數學模型,進而運用邏輯推理解決問題.
G632
B
1008-0333(2016)30-0035-01

