基于數形結合在高中數學中的應用解析
江蘇省靖江市斜橋中學(214500)
楊正輝●
?
基于數形結合在高中數學中的應用解析
江蘇省靖江市斜橋中學(214500)
楊正輝●
一、集合問題中數形結合思想的應用
對于集合的交、并、補等運算,往往都是采取集合運算中的數軸、韋恩圖進行計算,通過這樣的方式能使得題型簡化,從而將運算方式簡潔.
例1 已知集合A=[0,4],B=[-2,3],求A∩B.
解析 針對這兩個集合,可以在數軸上將其表示出來,那么,久能夠很明確的知道結果.
如圖1所示,我們很容易就看出A∩B=[0,3].
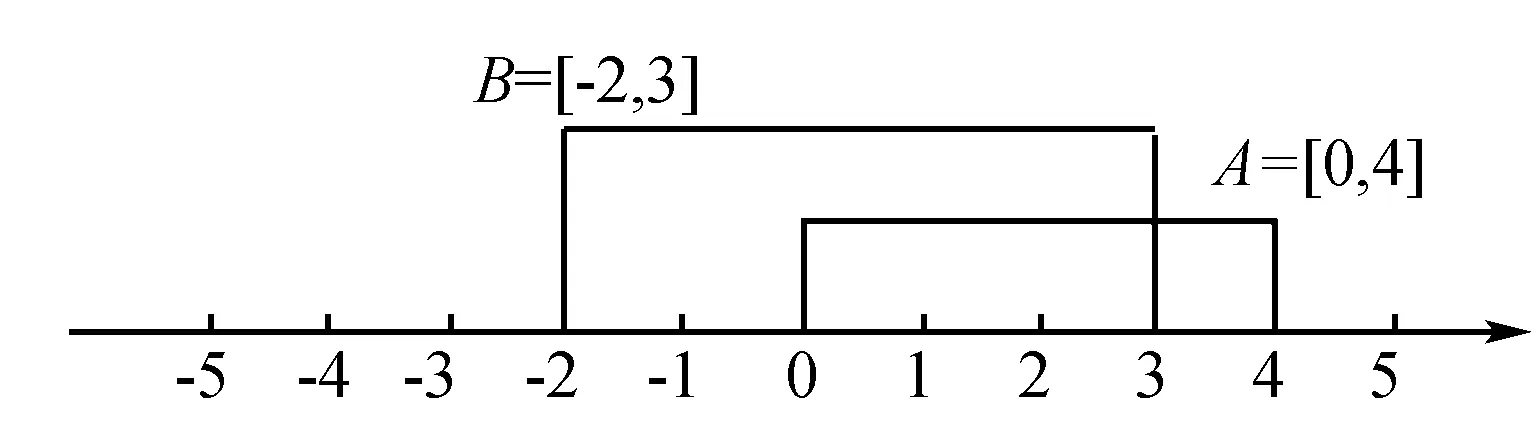
圖1
二、函數中屬性集合思想的運用
在高中數學教學中,函數是非常重要的一部分內容,它在教學中的作用于地位高于其他方式,而數形結合思想在進行解題時所發揮的效果也非常重要.
例2 函數f(x)是定于R上的偶函數,在(-∞,0]上是減函數,并且f(2)=0,那么不等式f(x)<0的解是____.
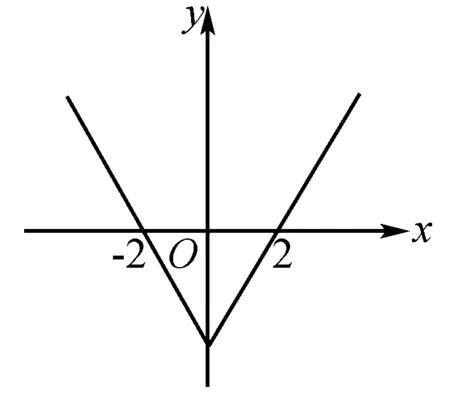
圖2
解析 結合題設條件畫示意圖圖2可知,f(x)<0的解集是(-2,2) .
三、通過使用數形結合求三角函數最值

四、復數中數形結合的應用
例4 設z∈C,并且|z|≤1/2,求|z+1|的取值范圍.
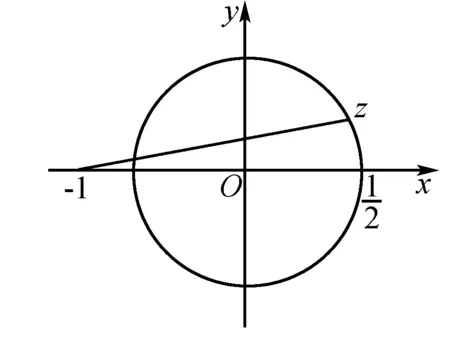
圖3
解 |z|≤1/2,表示以原點為圓心,半徑為1/2的圓及其內部,|x+1|表示點Z與點-1之間的距離.由圖3可見1/2≤|x+1|≤3/2.
五、幾何問題中數形結合的應用

A.1個 B.2個 C.3個 D.4個

圖4

由以上實例分析可知,通過利用圖形結合的方式,能夠將難解的題型簡化為容易分析的題型,能夠輕松將求解的問題得出,因此,想要貫通這些數形結合思想,在解題過程中需要重視以下方面內容:
(1)對于題型的圖形我們要善于觀察,對其中包含的數量關系一定要認知;
(2)需要學會繪制圖形,需要能清晰地將圖形中相應的數量關系表示出來;
(3)能夠掌握數與形兩者之間的相互關系,從而能夠將形轉變成數,能夠將數轉換成形;
(4)要做好應用數以及形之間的互化,將創造性以及靈活性思維提升.
總而言之,想要讓學生能夠掌握好數形結合思想的核心,那么就需要使得學生能夠有扎實的基礎,只有這樣,才能夠使得數形結合得到有效運用,進而能夠提升學生們的解題能力.
G632
B
1008-0333(2016)31-0047-01

