基于自適應遺傳算法的電子支援偵察搜索方式設計

杜 浩，畢大平，2，李敏樂

(1. 電子工程學院503教研室, 合肥 230037； 2. 安徽省電子制約技術重點實驗室， 合肥 230037)

?

·信號處理·

基于自適應遺傳算法的電子支援偵察搜索方式設計

杜 浩1，畢大平1，2，李敏樂1

(1. 電子工程學院503教研室, 合肥 230037； 2. 安徽省電子制約技術重點實驗室， 合肥 230037)

電子支援偵察是雷達對抗偵察的重要組成部分，主要借助已有情報信息對高威脅目標進行核實精測，對時效性和精確性具有較高的要求。傳統的搜索方式多為周期步進或區間搜索，與電子支援偵察的任務特性和搜索要求并未完全契合，面對不同環境和任務的靈活性較差。文中基于自適應遺傳算法對電子支援偵察的搜索方式進行設計：每一條染色體對應一種偵察搜索方式，染色體的基因值和基因位分別對應該時刻偵察系統的偵察區間和偵察系統在不同區間的停留順序，以截獲概率為適應度函數進行染色體的誘導變異，得到的最優染色體即為當前環境和任務下的最佳搜索方式。理論推導和實驗仿真驗證了該搜索方式的可行性和有效性。

電子支援偵察；遺傳算法；自適應搜索；截獲概率

0 引 言

雷達對抗偵察通常可以分為電子情報偵察、電子支援偵察和雷達告警等類型[1]。各類對抗偵察系統的目的都是為了獲取敵方輻射源(主要是雷達)的技術參數和戰術情報，但各類偵察方式的任務要求和應用背景有著較為顯著的差異。電子情報偵察多用于未知的長期情報搜集；電子支援偵察則主要用于特定戰場環境下重點目標群的搜索和驗證，目標情報信息通常較為詳實，但偵察時效性和精確性要求較高[2]。為了提高目標信號的截獲效率，需采用一定的搜索方式，對頻域和空域進行有側重的搜索。但在實際情報信息搜索過程中，兩種類型的偵察系統在搜索方式上并未嚴格區分，均采用周期性搜索或特定區間搜索。考慮到電子支援偵察是對特定目標情報信息的核實和精測，前期的偵察數據較為詳實，偵察記錄有跡可循，領域專家對目標有著較為充分的研究。因此，在信號的偵察過程中，應當可以結合目標數據庫、專家知識庫、已有偵察記錄等信息，針對性地引導偵察的頻率和方位，形成高效的搜索調度方法。

電子偵察的工作流程大致分為信號截獲、檢測、處理分析、輻射源識別[3]四個階段，而信號截獲是后續行動的先決條件。Self和Smith[4]較早對雷達信號的截獲問題進行了研究，通過采用窗口函數對信號的截獲事件進行建模，并根據統計平均的方式推導得到了周期信號最大截獲時間的計算公式，為搜索方式的選取和評估提供了重要依據。Vaughn I[5]以最大截獲時間為準則，采用數論和丟番圖近似的方法，對電子支援偵察的搜索方式進行了設計，通過對偵察系統在不同頻段的停留時間進行分配，有效避免了周期搜索方式下偵察目標和偵察系統之間的“同步問題”(同步指目標和偵察系統均采用周期掃描，二者的周期相近或成比例時，偵察系統很難截獲到目標信號的情況)。但避免同步現象僅提升了系統的搜索性能下限，搜索的實時性和靈活性仍有較大的提升空間。Edwin D[6]對先驗信息不充分情況下的優化搜索問題進行了研究，提出了基于連續時間馬爾科夫過程的隨機搜索方式，使偵察系統的最大截獲時間隨雷達掃描周期的增大而線性增長，但采用的搜索方式為隨機方式，搜索行為的可控性不強。Winsor C[7]采用遺傳算法對信道化接收體制的偵察系統進行了研究，為搜索方式的設計提供了新的思路，但由于算法設計中的適應度函數構建較復雜，遺傳算法未結合接收機特性進行改進，導致算法的收斂速度慢、偵察耗時較長。

本文在文獻[7]的基礎上，將搜索方式建模為遺傳算法中的染色體，將搜索方式的設計問題轉為對染色體尋優問題的求解。通過對遺傳算法的適應度函數進行重新設計，對染色體的交叉變異過程進行自適應誘導變異，改進了算法的適用性，提高了搜索方式在特定環境和任務要求下的針對性和靈活性。實驗仿真表明：該方法相比傳統搜索方式，對電子支援偵察系統的截獲性能提升較為明顯。

1 偵察截獲模型建立

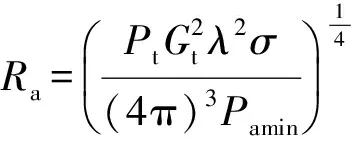
圖1所示為三窗口函數的示例，窗口函數1表示雷達的天線轉動規律，函數峰值表示該時間段雷達天線波束照射到偵察系統；窗口函數2表示偵察系統的頻率搜索規律，函數峰值表示該時間段偵察系統的頻率覆蓋范圍包含對方雷達的工作頻率；窗口函數3表示偵察系統的天線轉動規律，函數峰值表示該時間段偵察系統天線波束照射到雷達。三個窗口函數的重合部分表示該時間段內偵察系統能夠截獲到雷達信號。

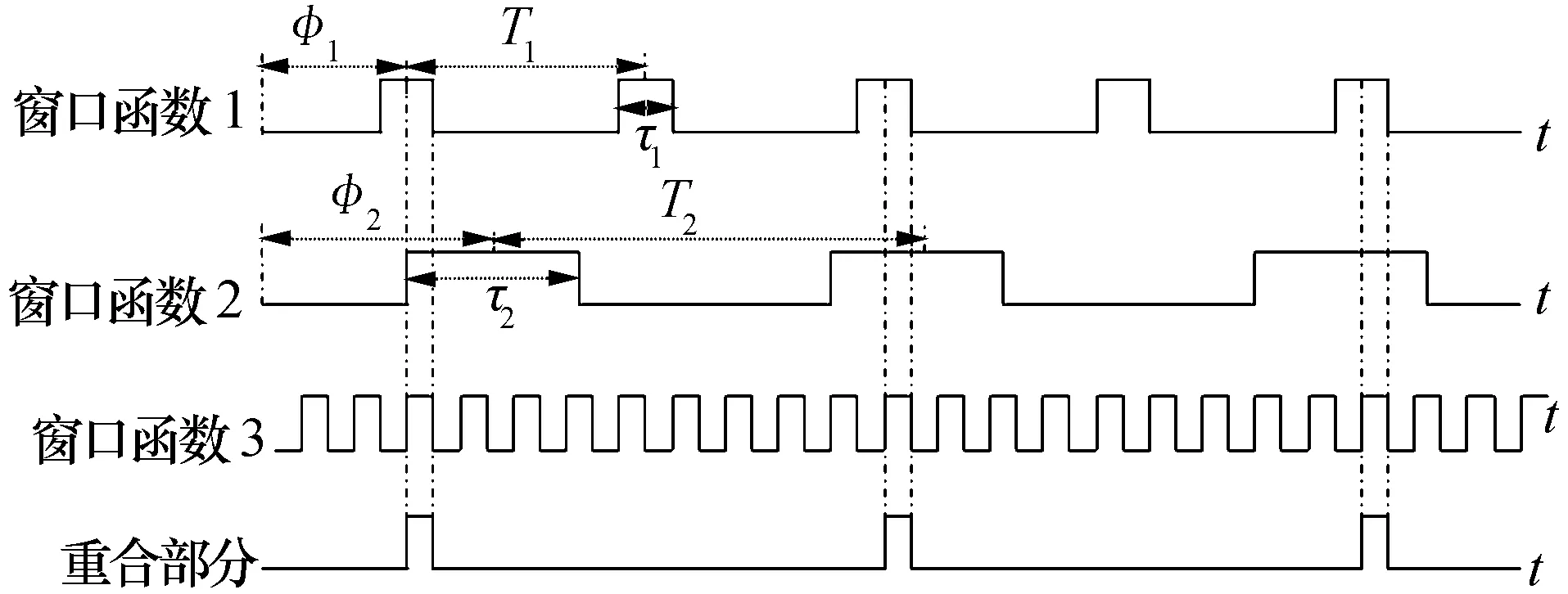
圖1 將不同維度的截獲條件用窗口函數表示

2 基于遺傳算法的搜索方式設計

2.1 自適應遺傳算法原理

遺傳算法借鑒了“優勝劣汰”的自然界法則，是一種并行的隨機搜索算法，被廣泛應用于人工智能、系統仿真、運籌管理等領域[9-11]。但遺傳算法自身存在不少待完善的地方，尤其是算法的收斂速度和收斂性之間存在矛盾。受生物學中人工誘導變異方法的啟發，采用誘導變異方法對算法進行改進。

如圖2所示，為了提升后代染色體的適應度，本文在交叉變異環節，根據適應度函數確定出適應度較大的個體，對該部分個體進行分析得到各染色體的基因序列，并對各基因值和對應位置的出現規律進行統計。統計得到的出現概率較高的基因值和所在染色體的位置即為優秀基因值和基因位。在本文的應用背景下，優秀基因值和基因位置表明，在該時刻偵察系統如果對基因值對應的頻率區間進行偵察更有可能截獲到目標，它們為偵察系統的最佳搜索行為提供了具體的建議。

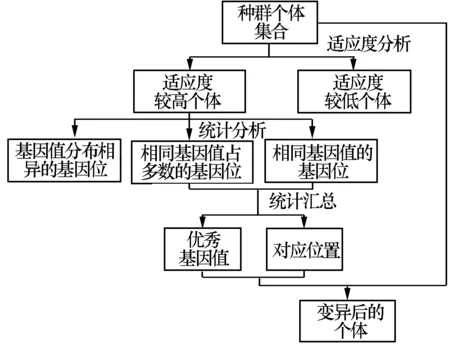
圖2 誘導變異方法流程

2.2 搜索方式模型建立

信道化接收機具有良好的頻率選擇性、高靈敏度和寬瞬時頻率覆蓋范圍，典型的信道化接收機可以瞬時覆蓋偵察頻域的10%～20%。將偵察頻域根據信道化接收機的瞬時頻率覆蓋范圍進行等間隔劃分，則信道化接收機的搜索只需在5～10個偵察區間進行切換。根據遺傳算法的理論，遺傳算法中的每一條染色體對應一種偵察搜索方式，染色體的每一個基因由整數構成，對應該時刻偵察系統正在偵察的頻率區間，基因在染色體上的排列次序對應偵察系統在不同區間的停留順序。圖3所示為搜索方式與染色體的對應關系，根據偵察系統的瞬時頻率覆蓋范圍將待偵察頻域均勻劃分成10個區間，并予以編號，偵察系統單位時間內僅對某一區間進行偵察。遺傳算法生成的染色體長度與偵察所需的總時間相等，染色體上的基因位置對應偵察的具體時刻，基因的數值(取整數0～9)對應該時刻偵察系統的偵察區間，通過構建染色體可對偵察系統的每一個時刻的偵察行為進行精確控制。

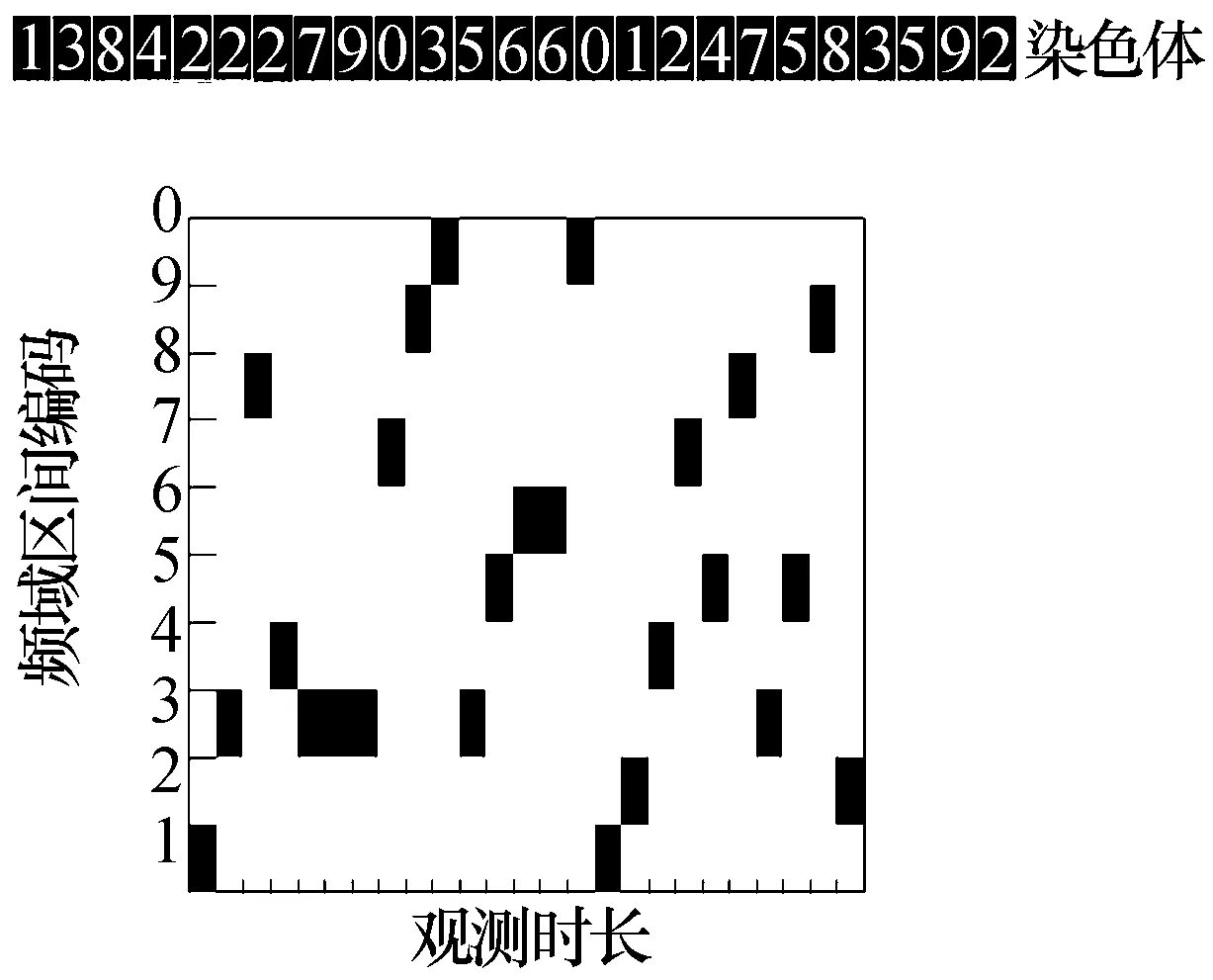
圖3 搜索方式與染色體的對應關系

2.3 算法適應度函數設計

由于偵察策略主要用于短時間內特定目標群的精測和驗證，適應度函數采用各目標截獲概率的加權和P。

目前通用的截獲概率計算方法是將各維度的截獲事件采用泊松流描述，根據各窗口函數的平均窗口寬度τi和平均搜索周期Ti進行計算，T時間內k次截獲的概率為[12]

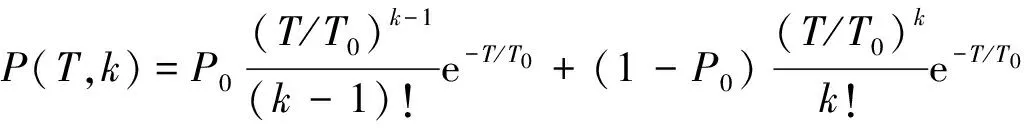
T≥0, k=1,2,…

(1)

考慮到遺傳算法生成的初始種群為一系列隨機數列，每個數字的重現頻率不滿足周期性，采用式(1)計算將存在較大的誤差，不能正確反映截獲性能。

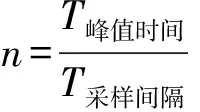
如圖4所示，現將各維度窗口函數經過采樣得到0和1組成的數列，將染色體分別按照是否停留在特定頻率區間化為若干條數字序列(數列只有0和1構成，1表示該時刻停留在區間內，0表示不在該區間)，將各數列按位進行“與”運算，對運算得到的數列中數字1的位置和數目進行統計分析。1的數量和連續出現的位數為成功截獲該雷達信號的次數和截獲的持續時間。

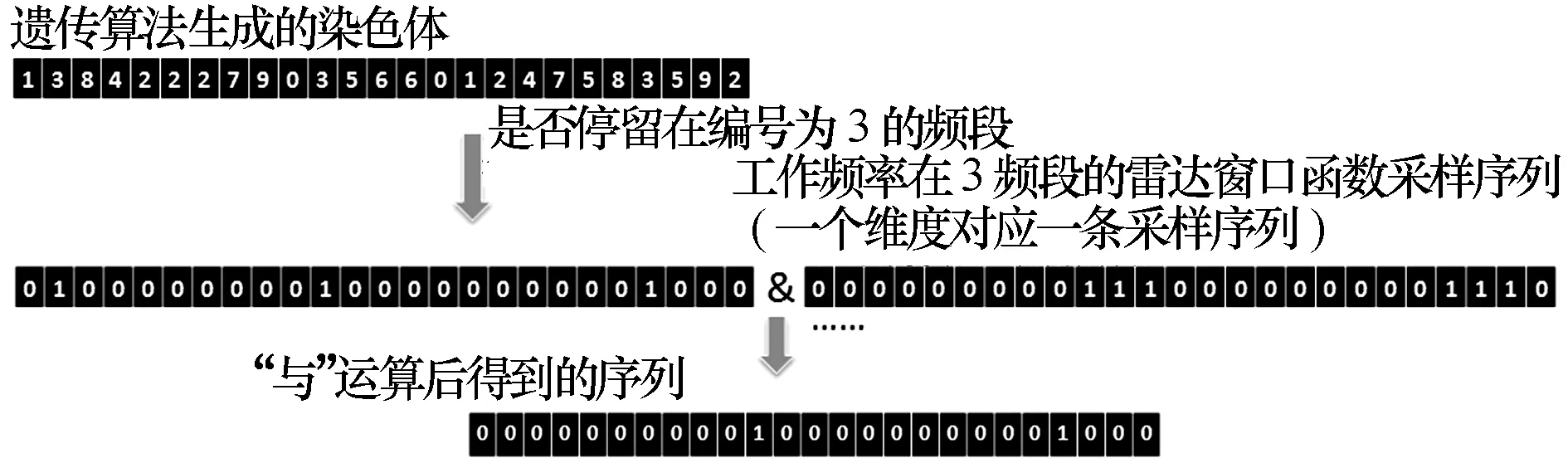
圖4 染色體與窗口函數采樣序列的運算過程

實際情況下，雷達的開機時間無法獲取，即空域窗口函數的初始相位φi無法確定，需要根據采樣精度對初始相位不同取值下的截獲情況逐一統計，將能夠截獲目標的取值個數除以總取值個數，即為該目標的截獲概率pi

(2)

式中：Na為初始相位的取值個數；Nb為數列R(φj)的位數；R(φj)為初始相位φj條件下各數列“與”運算的結果。

總截獲概率P的計算公式為

(3)

式中：hi為目標的優先級(取值越大，優先級越高)；pi為目標i的截獲概率；N為待偵察目標的個數。

2.4 算法運算步驟

步驟1 確定染色體長度、基因的取值范圍，產生初始種群；

步驟2 計算種群的適應度，并按升序排列，分別用B1(t)～B10(t)表示；

步驟3 分別對B3(t)～B10(t)進行優秀基因位的統計，將優秀基因值保存到T3～T10；

步驟4 根據步驟3中的T3～T10的值對B3(t+1)～B10(t+1)誘導變異[13]。隨機產生2個新個體賦值給B1(t+1)和B2(t+1)；

步驟5 判斷是否達到設定的迭代次數，達到則結束，否則t=t+1，執行步驟3。

3 理論分析和場景仿真

3.1 算法收斂性分析

根據算法的運算步驟可知，種群在第t+1代的狀態只與第t代種群狀態有關，與之前的代數無關，種群是有限集，故可以采用有限齊次馬爾科夫過程進行分析描述[14]。

以Xi表示t=i時刻的狀態，以Pi表示處于狀態Xi的概率，以Pi,j表示狀態Xi→Xj的轉移概率，P表示狀態轉移矩陣。

(4)

則

(5)

又

(6)

將上式代入，則

(7)

又

(8)

綜上可得

(9)

即迭代次數足夠大時，文中的算法能搜索到全局最優值。

3.2 場景仿真及分析

下面對本文的搜索方式通過場景仿真，進一步分析截獲性能。某次偵察任務，需要在盡可能短的時間內對下列11部雷達的工作參數和開機與否進行精測和核實。偵察目標工作參數如表1所示。

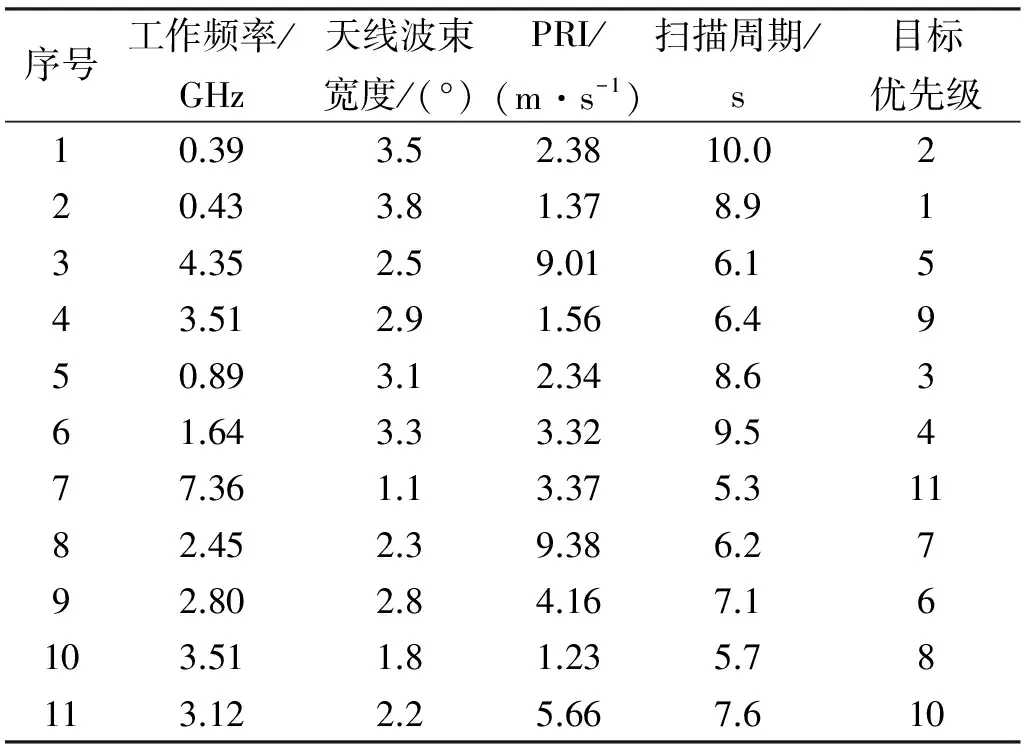
表1 待偵察目標清單

偵察系統采用信道化體制的接收機，瞬時頻率覆蓋范圍為600 MHz，偵察范圍為0.3 GHz～8 GHz。分別針對常規周期往復搜索方式(搜索行為如圖5所示，對應的截獲概率為P1)、只在目標群所在頻率區間(以下簡稱參考區間)周期往復搜索(搜索行為如圖6所示，對應的截獲概率為P2)和基于遺傳算法的搜索(P3)三種方式，每個頻率區間的停留時間為0.1 s和0.05 s兩種情況下，相同觀測時長時的截獲性能進行比較分析。

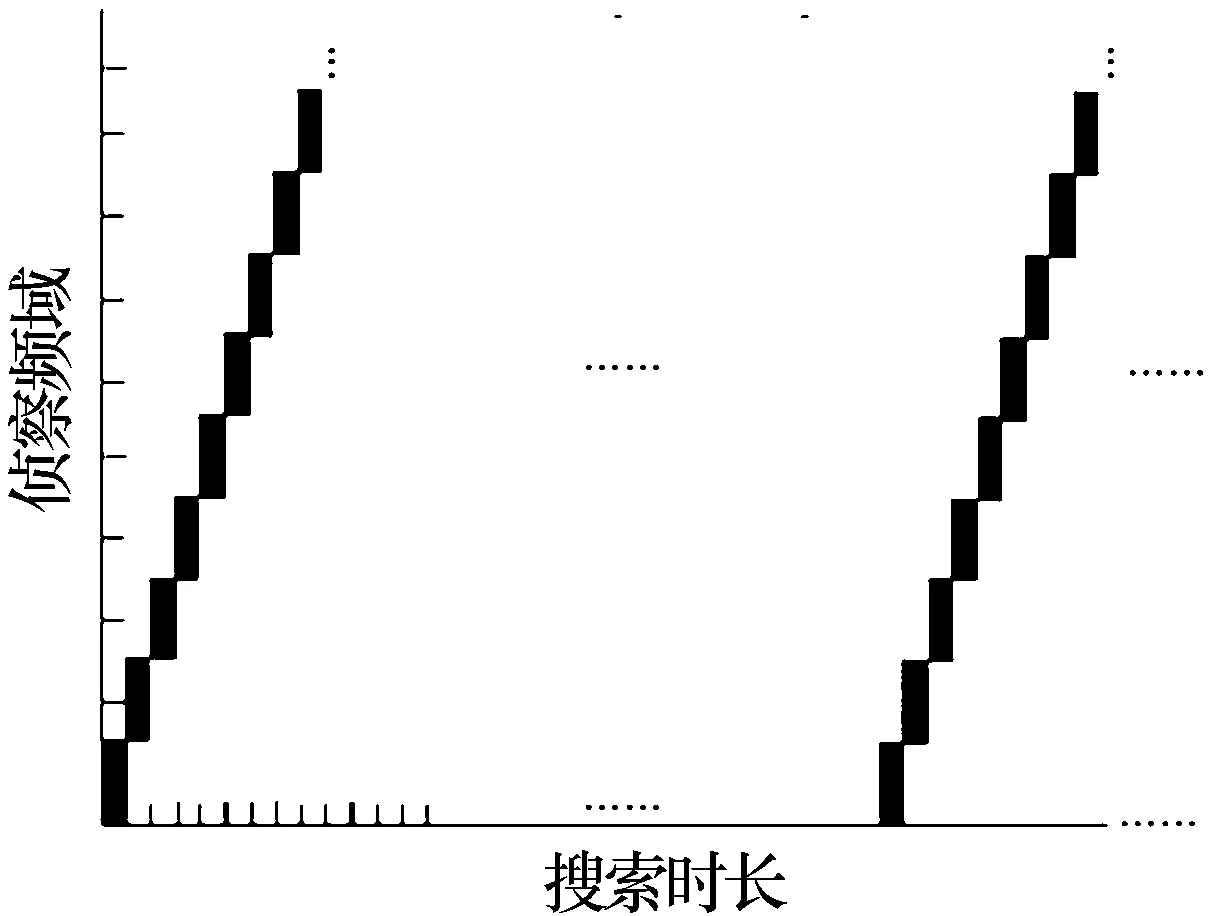
圖5 常見周期往復搜索示意圖

圖6 參考區間周期往復搜索示意圖

圖7、圖8所示分別為停留時間是0.05 s和0.1 s時三種搜索方式的性能對比。

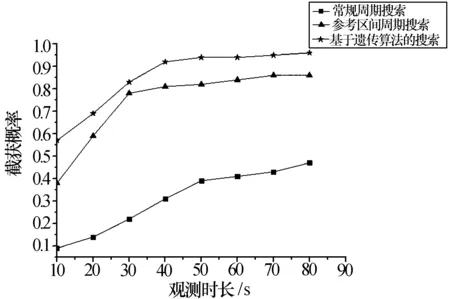
圖7 單次停留時間為0.05 s時搜索方式性能對比

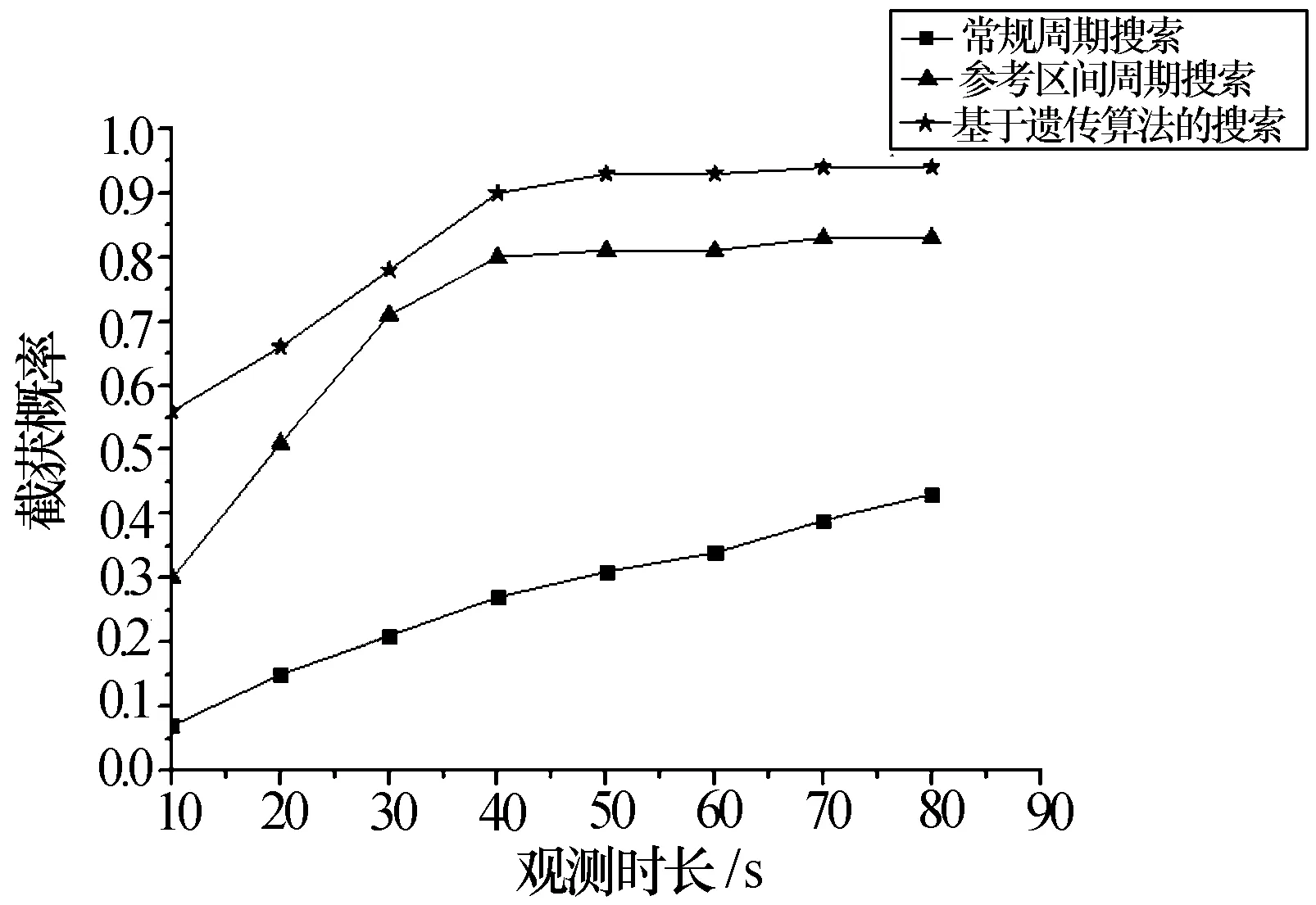
圖8 單次停留時間為0.1 s時搜索方式性能對比

通過分析可得到如下結論：

(1)三種搜索方式中，基于遺傳算法的搜索方式截獲概率是最高的。這是因為提高截獲概率的關鍵是提高各窗口函數的峰值重疊部分。對于周期往復的搜索方式，各窗口函數的形狀均是固定的，若要提高峰值的重疊部分只能借助增加搜索時間，不能對窗口函數的峰值長度和峰值位置進行調整；基于遺傳算法的搜索方式，通過多代遺傳變異得到最優染色體，偵察系統對應的窗口函數的峰值長度和峰值位置得到了針對性的設計，當搜索時間延長時，峰值的重疊部分會增加的很快，由此實現高截獲概率。

(2)單次停留時間為0.05 s時的搜索方式截獲概率略高于停留時間為0.1 s的搜索方式。采用較短的停留時間進行周期搜索，能夠提高偵察系統對不同區間的搜索頻次，同樣可以提高對不同窗口函數的重合機會，但停留時間不應過短，否則窗口函數的峰值部分會太小，不利于實現與其他窗口函數的峰值匹配。基于遺傳算法的搜索方式，停留時間減小，則對應染色體上的基因數目增多，從而使基因排布的靈活性增強，頻率搜索的控制精度增高，減少了時間上的浪費；但與此同時，對遺傳算法的收斂速度要求更高(需要更多的進化代數才能得到最優解)。

(3)常規搜索的截獲概率隨時間的增幅比較恒定，而后兩種方式在觀測超過40 s后，截獲概率的增長速度均放緩。P3的增長放緩是由于此時截獲概率已經趨近于1，算法的尋優結果趨于穩定。P2增長的放緩是由于截獲概率是11個偵察目標截獲概率的加權和，天線波束寬度寬、脈沖重復間隔(PRI)短的目標能夠隨觀測時間的增長實現高截獲概率；但天線波束寬度窄、PRI長的目標，對應維度的窗口函數的峰值部分短、重復周期長，短時間內不易實現各函數峰值的重合；隨著觀測時長的增加，部分目標的截獲概率增長較快，短時間內達到很高的值，而另一部分目標較難截獲，單純增加觀測時長，效果不明顯。P1的增長趨勢比較穩定是由于該搜索方式尚未對容易搜索到的目標實現最佳截獲，可以預見，當觀測時間繼續增大時，P1的后續增長也會出現同P2相似的情形。

(4)觀測時長變長，三種搜索方式的截獲概率均增大。這是由于觀測時間增大，不同維度的窗口函數實現重合的機會變多。

圖9所示為單次停留時間為0.05 s，觀測時長分別為10 s、20 s、30 s、40 s時遺傳算法的性能曲線。不同觀測時長下的初始截獲概率的大小處于常規周期搜索和參考區間周期搜索兩種方式的性能之間，經過140代左右的進化，算法的性能逐漸穩定，最終截獲概率較初始值提高了0.2左右，迭代過程中有時會陷入局部收斂，但由于采用了自適應誘導變異經過20代左右的時間能夠擺脫局部收斂。

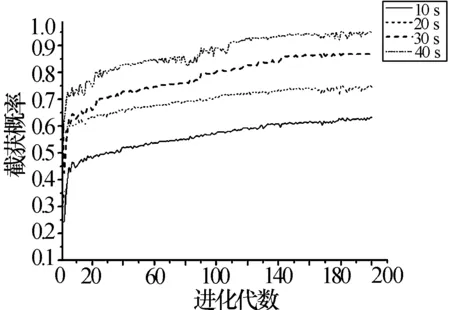
圖9 基于遺傳算法的搜索方式性能(停留時間為0.05 s)

4 結束語

本文主要研究了一種基于改進型遺傳算法的雷達對抗偵察搜索方式。適應度函數的設計采用對窗口函數采樣、采樣數列進行“與”運算、運算得到的數列按位相加統計等步驟，為非周期搜索方式下的截獲概率計算提供了一種快捷可行的求解途徑。通過自適應誘導變異提升了遺傳算法的性能。基于改進型遺傳算法的搜索方式利用了信道化接收機的寬瞬時頻率覆蓋范圍等優點，使偵察系統能夠根據當前環境下的搜索任務采取針對性地搜索方式，相較傳統的周期性步進搜索方式提高了重點目標群的截獲概率，減少了搜索時間，為后續的信號處理奠定了良好的基礎。

[1] WILEY R G. 電子情報(ELINT): 雷達信號截獲與分析[M]. 呂躍廣, 譯. 北京:電子工業出版社, 2008. WILEY R G. Electronic intelligence: radar signal acquisition and analysis [M]. Lü Yueguang, translate. Beijing: Pubishing House of Electronics Industry, 2008.

[2] 姜秋喜. 網絡雷達對抗系統導論[M]. 北京: 國防工業出版社，2010. JIANG Qiuxi. Introduction to network radar countermeasure systems[M]. Beijing: National Defense Industry Press, 2010.

[3] VAUGHN I. CLARKSON L. The farey series in synchronization and intercept-time analysis for electronic support[J]. Transactions of the AOC, 2004, 1(1): 7-28.

[4] SELF A G, SMITH B G. Intercept time and its prediction[J]. IEE Proceedings,1985,13(2): 215-220.

[5] VAUGHN I, CLARKSON L. Optimization of periodic search strategies for electronic support[J]. IEEE Transactions on Aerospace Electronic Systems, 2011, 47(3): 1770-1784.

[6] EDWIN D. MAHASSNI E, STEPHEN D, et al. A markov-chain model for sensor scheduling in electronic support[J]. IEE Proceedings of Radar, Sonar & Navigation, 2006, 153(4): 325-332.

[7] WINSOR C, HUGHES E J. Optimization and evaluation of receiver search strategies for electronic support[J]. IET Radar, Sonar and Navigation, 2012, 6(4): 233-240.

[8] 胡來招. 雷達偵察接收機設計[M]. 北京: 國防工業出版社, 2000. HU Laizhao. Design for radar reconnaissance receivers[M]. Beijing: National Defense Industry Press, 2000.

[9] 楊正龍, 張 銳, 楊文軍, 等. 基于遺傳算法的網格化球頂相控陣波束綜合[J]. 現代雷達, 2016, 38(3): 70-74. YANG Zhenglong, ZHANG Rui, YANG Wenjun, et al. Radiation pattern synthesis for geodesic dome phased array antenna based on genetic algorithm[J]. Modern Radar, 2016, 38(3): 70-74.

[10] 朱 玲, 江朝抒, 陳祝明,等. 基于矩估計的遺傳算法雜波幅度模型參數估計[J]. 現代雷達, 2009, 31(12): 53-56. ZHU Ling, JIANG Chaoshu, CHEN Zhuming, et al. Genetic algorithm applied to parameter estimation for clutter amplitude model based on MOM[J]. Modern Radar, 2009, 31(12):53-56.

[11] 王 鵬, 譚賢四, 王 紅,等. 基于遺傳算法的地面中重頻PD雷達PRF組選擇[J]. 現代雷達, 2008, 30(9): 33-35. WANG Peng, TAN Xiansi, WANG Hong, et al. PRF set selection for ground-based MPRF PD radar based on generic algorithm[J]. Modern Radar, 2008, 30(9): 33-35.

[12] 趙國慶. 雷達對抗原理[M]. 西安: 西安電子科技大學出版社, 2012. ZHAO Guoqing. Principles of radar countermeasure[M]. Xi′an: Xidian University Press, 2012.

[13] 梁亞瀾, 聶長海. 覆蓋表生成的遺傳算法配置參數優化[J]. 計算機學報, 2012, 35(7): 1522-1538. LIANG Yalan, NIE Changhai. The optimization of configurable genetic algorithm for covering arrays generation[J]. Chinese Journal of Computers, 2012,35(7): 1522-1538.

[14] 曹 凱, 陳國虎, 江 樺. 自適應引導進化遺傳算法[J]. 電子與信息學報, 2014, 36(8): 1884-1890. CAO Kai, CHEN Guohu, JIANG Hua. Guided self-adaptive evolutionary genetic algorithm[J]. Journal of Electronics & Information Technology, 2014,36(8):1884-1890.

杜 浩 男，1990年生，碩士研究生。研究方向為電子對抗裝備。

畢大平 男，1965年生，教授，博士生導師。研究方向為電子對抗裝備新技術。

李敏樂 男，1992年生，碩士研究生。研究方向為雷達對抗偵察技術。

Search Strategy Design for Electronic Support Measure Based on Adaptive Genetic Algorithm

DU Hao1，BI Daping1,2，LI Minle1

(1. Department of 503, Electronic Engineering Institute, Hefei 230037, China)(2. Key Laboratory of Electronic Restriction, Anhui Province, Hefei 230037, China)

Electronic support measure is an important part of radar reconnaissance, mainly through existing intelligence information on the high level threat emitters to make high precision measurement or verification. Such operation heavily demands on timeliness and accuracy. Traditional search mode tends to be periodic pattern or stayed on certain region, which is not fully fit with the emitters' characteristics or the task requirement and possesses poor flexibility. Based on the adaptive genetic algorithm, this paper designs and analyzes the search strategy of electronic support measure. Each chromosome corresponds to a search strategy; the gene value of the chromosome and the position of the gene corresponds to the search intervals and the dwell sequence of search strategy separately. Based on the fitness function, which is calculated by the intercept probability, chromosomes take induced mutation to find the optimal offspring which is also the desired search strategy confronted with the current environment. Theoretical derivation and experimental simulation verify the feasibility and effectiveness of this method.

electronic support measure; genetic algorithm; adaptive search; intercept probability

10.16592/ j.cnki.1004-7859.2016.11.005

杜浩 Email：kevindu0930@163.com

2016-08-15

2016-10-13

TN957.51

A

1004-7859(2016)11-0018-06