立體幾何最值問題的拓展探究

◇ 江蘇 劉 震 梁 兵

立體幾何最值問題的拓展探究

◇ 江蘇 劉 震 梁 兵

立體幾何中的最值問題是高考常考題型,其中體積最值問題又是重中之重.此類試題的命制通常以定理及其基本圖式為基礎、空間想象能力為依托、位置關系轉化為基本思維模式,通過構造函數求最值.下面引例說明.

例 在棱長為1的正方體ABCD-A1B1C1D1中,P1、P2分別是線段AB、BD1(不包括端點)上的動點,且線段P1P2∥平面A1ADD1,則四面體P1P2AB1的體積的最大值是( ).

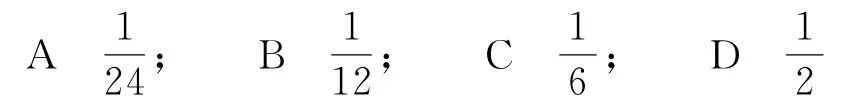
本題以正方體為背景,線線、線面平行為依托,體積最值的求解為目標,意在考查同學們對空間圖形的識別、應用能力.解答本題的基本策略:空間問題平面化、函數思想、化歸轉化等綜合應用.

1 提取信息,理順關系

信息1:如圖1,已知P1、P2分別是線段AB、 BD1(不包括端點)上的動點且線段P1P2∥平面A1ADD1,由線面平行的性質可知P1P2∥AD1.

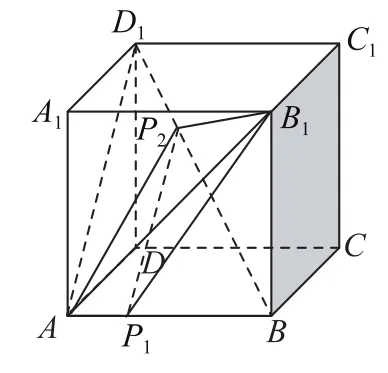
圖1

信息2:所求四面體P1P2AB1的體積的最大值,即為三棱錐B1-P1P2A體積的最大值,而此三棱錐的高為點B1到面P1P2A的距離,即為點B1到面ABD1的距離,此距離為定值,故體積最值問題即為底面△P1P2A面積的最值問題.

2 空間化平面,探究最值

欲求△P1P2A面積的最大值,可將△ABD1從立體幾何圖形中提取出來,如圖2所示,由已知可得AB⊥AD1,點P2的BD1上運動,隨著P2位置的改變,△P1P2A的面積隨之改變,因此將問題轉化為運動過程中求△P1P2A面積的最值.

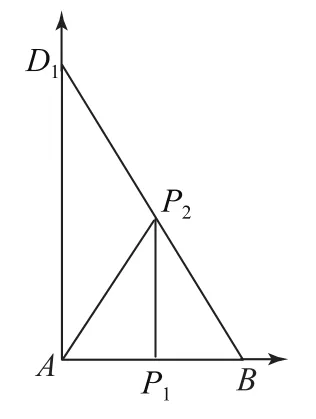
圖2

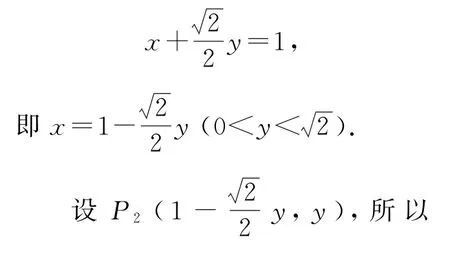
3 等價轉化,探究空間距離

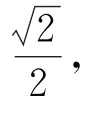
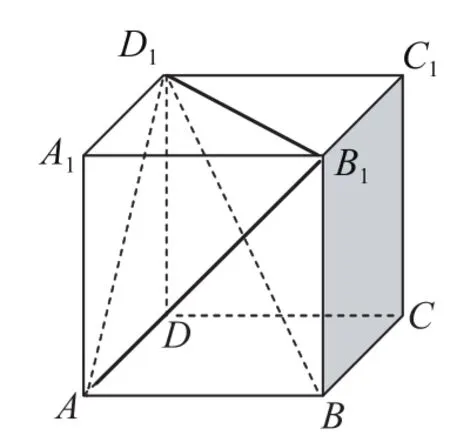
圖3

轉換視角,以A為頂點,則三棱錐A-BB1D1的底面的面積為高為點A1到直線B1D1的距離所以三棱錐A-BB1D1的體積

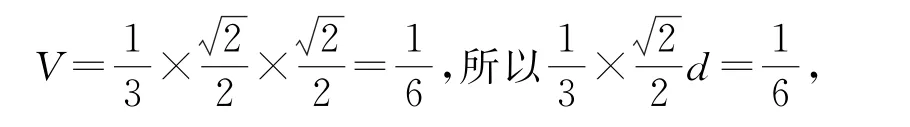
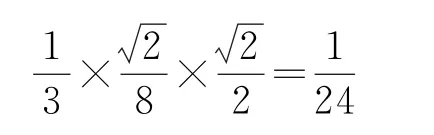
即為所求.綜上可知正確選項為A.

解決立體幾何中的最值問題不僅要具備較強的空間想象能力,而且還要會靈活運用代數、幾何、三角等相關知識.此類問題既富思考情趣,又融眾多知識和技巧于一體,綜合性強、靈活性高、難度較大.充分體現了變知識立意為能力立意、在知識網絡交匯點處設計試題能力的高考命題指導思想,是考查考生數學能力和數學素養的極好素材,應引起我們足夠的重視.

(作者單位:江蘇揚州市廣陵區紅橋高級中學)