談解析幾何數學實驗課的教學設計

石向東

(梧州學院 信息與電子工程學院，廣西 梧州 543002)

?

談解析幾何數學實驗課的教學設計

石向東

(梧州學院 信息與電子工程學院，廣西 梧州 543002)

基于知識性、實踐性、操作性和計算機為一體的數學實驗教學是一種有利于提高學生創新能力和綜合素質的新的數學課程。文章根據解析幾何學科特點，提出數學實驗課教學設計的原則和課程設置方法。

解析幾何；數學實驗；教學設計；數學軟件

1引言

隨著現代社會由工業社會向信息社會過渡，國家教育部對高校培養目標及人才培養模式提出了新的要求，在高校中培養有創新能力的高素質人才已成為高等教育改革的核心問題，如何對現有教學進行改革以適應社會對人才的需求而成為高等教育的一項迫切而重要的任務。教育部在《進一步深化本科教學改革、全面提高教學質量的若干意見》中明確指出：“要堅持知識、能力和素質協調發展，繼續深化教學內容和教學方法等方面的改革，實現從注重知識傳授向更加重視能力和素質培養的轉變”，要“著力培養學生創新精神和創新能力。”解析幾何在大學數學中有著重要的地位和作用，它是理工科各專業的基礎課，又是培養學生數學思維的極好教材，在當前教學改革的浪潮中，解析幾何教學應朝著實現提高學生數學素養、培養創新能力的方向轉變。

2解析幾何課堂教學的特點

傳統的解析幾何課堂教學有著比較成熟的教學設計與模式，教學上注重理論的系統性和完整性，以嚴密的演繹思維、邏輯推理為研究方式，充分提高了學生的思維水平，體現了解析幾何的理論價值。不可否認，課堂教學模式為國家培養了大批優秀人才，這是它的精華之處。

但是，傳統的課堂教學忽視了對學生主動思考、自主創新能力的培養。其不足之處有如下3點。

2.1重傳授，輕探索

課堂教學的方法主要是講授法，在教學過程中，教師有條不紊、富有啟發性地逐層深入講解，加以布局合理的板書，把解析幾何課程中的定理證明、公式推導、曲線與曲面的一般理論，通過演示、推理、說明和計算，使學生緊跟老師的思路，學到了系統而完整的解析幾何理論知識。

在這種“傳授”理念下的課堂教學，教師往往是站在知識系統化的角度去展開教學，一開始就將問題引向概念，進而提出概念的抽象表述與符號化表示方式，然后再灌輸一大堆解題技巧。學生則被動地接受這些抽象的教學理論，并機械地記住有關解題方法以應付考試。這種以教師注入式的講解代替學生思維活動的教學方式，只會導致學生不會獨立思考，更不會主動探索地學習。與被動地接受教師傳授的學習方式相比，主動探究的學習方式在培養學生實踐能力、創新能力方面更具有深遠意義。自主探究的學習方式將學生置于一種主動探索并注重解決問題的學習狀態中，通過自己動手、動腦、實驗等活動來了解知識的形成和發展過程。建構主義學習理論認為學生是學習活動的主體，是自己認知結構建構的決定者[1]。學生學習的主動性能否得到充分發揮，直接影響到知識建構活動的質量與效率。

2.2重演繹，輕歸納

數學的特征之一是邏輯嚴密性，如嚴謹的歐幾里得幾何，從幾個公理出發，以演繹推理方式引出了一系列的命題，構成了一個公理化的幾何論證體系，進而表現這個理論所揭示的真理，所以說數學是演繹的科學。但演繹性僅是數學的一個側面，它的另一個側面是歸納性。歸納推理方法由個別推及一般，由已知推及未知，所以它具有探索和發現新的數學問題和數學理論的功能。如同其他自然科學一樣，數學的起源也依賴于歸納推理，因此從數學發展過程而言，數學是歸納的科學。

在解析幾何教學中，要全面提高學生的數學素養，就必須既教演繹推理，又教歸納推理，但傳統的課堂教學，只重視演繹思維訓練，卻忽視歸納思維的培養。

解析幾何教材提供的是數學知識的邏輯系統，它所表現的定理證明過程是經過邏輯加工的演繹體系，同時教師也是通過“定義—定理—推論”這條演繹推理模式把“結果”傳授給學生，這種演繹思維的順序恰與數學家們在發現這些“結果”的研究活動中的歸納思維順序相反，在這里看不到數學家創造性活動中的猜想、聯想、類比、歸納等合情推理過程。

2.3重理論，輕實踐

以單純教學系統的、完整的解析幾何理論為主，忽視對學生的實踐能力的培養，是解析幾何傳統的課堂教學的又一個特點。實踐是培養人的能力和智慧的搖籃，這是與學習書本知識不同的另一種學習方式，學習者在實踐中體驗，在實踐中獲得能力。隨著高科技的迅速發展，數學思想已滲入到其他科學領域以及各個行業。社會對數學的需求，體現在既需要掌握數學理論的數學工作者，更需要善于運用數學知識及數學思維去解決實際問題、取得社會效益、有實踐能力的人。

3在解析幾何中開設數學實驗課的必要性

解析幾何的教學目標是培養學生的邏輯思維、空間想象能力，進而培養他們的實踐和創新能力，這種創新能力可以概括為善于應用新技術獲取和處理信息的能力、主動探究能力、分析和解決問題的能力。要培養這些能力，僅靠傳統的課堂教學模式和原有的學習方式是難以勝任的。課堂教學只注重培養學生嚴密的邏輯推理能力，只注重傳統系統的數學理論知識的傳授，而忽視實踐能力和創新能力的培養，這與國家對理工科大學生的高素質要求相差甚遠。

數學實驗室是一種開放式的、在數學思維活動參與下的、在特定的實驗環境中進行的教學方式。數學軟件強大的計算功能和圖形可視化功能為學生提供了一個圖文并茂、直觀生動的教學環境[2]。一方面，它使一些在課堂教學中難以表達的抽象理論或無法觀察到的現象如動點軌跡的形成、空間曲線的生成、曲面性質以直觀形象或動畫演示的方式展示出來，有效地突破了解析幾何課堂教學中的難點，幫助學生深層次地理解數學理論。另一方面，學生在實驗環境中動手做實驗，學會猜想，學會探索，培養了創新思維能力。因此，數學實驗課是課堂理論教學的有益補充，在解析幾何教學中開設數學實驗，是適應國家對人才的綜合素質要求所作的改革舉措。

4數學實驗課程的設計原則

4.1實驗內容取自解析幾何教材的原則

根據開設數學實驗的宗旨，我們認為數學實驗教學內容主要是圍繞解析幾何的基礎理論。數學實驗課程的載體是“問題”，從“問題”出發，以解決“問題”為線索組成實驗課的課程內容，這些內容都出自解析幾何教材中，可以是一些概念、定理，也可以是空間曲線、曲面性質等。數學實驗除了驗證一些基本結論外，對于注重創造性思維培養的探索性實驗，應有意識地去選擇一些能讓學生自己動手的計算機實驗，并通過歸納推理等思維活動去發現結論的解析幾何基本知識。

4.2數學實驗與解析幾何課堂教學進度同步開設原則

數學實驗課與理論課一起開設，并保持相適應的進度，并且安排的課時必須適量。在不影響解析幾何理論教學的前提下，我們認為開展4個課時的實驗教學課較適中。圍繞解析幾何理論的教學內容以插入形式開設。經參考其他院校的數學實驗教學大綱，我們對數學實驗課程的安排大致為：第一次實驗課安排在第二章軌跡與方程；第二、第三次安排在第四章，目的使學生在數學實驗中用實驗方法去探究曲線或曲面性質；第四次則安排在第五章進行。

4.3操作性與探索行相結合原則

數學實驗課是一門強調實踐與探索的課，具有很強的操作性,學生通過數學實驗，自主探究，合作交流，也就通過“做”數學去探究數學規律。這是一個動手與動腦相結構性合的過程，因此要把握“做”的度，不能只顧操作性而忽視數學思維探索性的培養，要求學生既能運用計算機得到相應的數據，又能對數據進行數學分析并得出結論[3]。

4.4實驗課題的選擇與教學目標相匹配原則

作為解析幾何課程的數學實驗，其著眼點除了通過自主探索與實踐達到培育創新能力外，還應通過數學實驗掌握解析幾何相關概念與定理，如圍繞曲面截痕軌跡的形成使學生學習曲面的形狀與性質，圍繞維維安尼曲線的畫法掌握空間曲線的射影柱面的來龍去脈與性質等等。

5解析幾何數學實驗課的教學設計

國內開設數學實驗課主要有兩種形式，一種是獨立開課，即指獨立于大學數學各基本課程之外，單獨開設數學實驗課程，另一種是在各基礎課程的教學中引入數學實驗課，把它作為各數學基礎課程的教學環節[4]，根據學校的具體情況和解析幾何教學改革的現狀，我們采用后一種形式。

與把數學實驗作為一門獨立的課程來開設不同，作為引入解析幾何課的數學實驗，定位為讓數學實驗與解析幾何課堂教學優勢互補，掌握解析幾何的基本理論和學習方式培養他們的探索精神和創新能力，因此數學實驗的內容都取自解析幾何教材，包括某些概念、定理、公式等。按教學方式、教學目的以及思維訓練水平來分，我們將實驗分為兩種：一種是驗證實驗，用計算機驗證一些已學的結論或公式；另一種是探索實驗，強調探索一些復雜的解析幾何定律或公式。前者著眼于“結果”的驗證，后者著眼于“結果”的發現[5]。

5.1驗證性實驗

解析幾何課堂教學已把數學理論傳授給學生，如概念、定理等，但學生往往對這些知識的理解是抽象的、片面的、生疏的。在數學實驗課上，通過學生自己動手以實驗檢驗這些已知的結論的正確性，幫助學生更好地理解和掌握解析幾何的基本理論。許多空間曲線和曲面的形成，是無法由教師在課堂上用靜態的示圖和口頭語言講清的，計算機“可視化”的動態演示，把曲線或曲面的形成過程準確地模擬出來，對提高學生的空間觀念、數形結合思想水平和教學效果起到事半功倍的作用。

案例1：演示動點或動直線的軌跡的生成。

動點或動直線的軌跡是解析幾何又一難點。利用matlab的圖形可視化功能，可以把軌跡的形成過程準確地模擬出來，對提高學生的空間觀念有很好的效果。

例：有兩條相交的直線l1與l2，其中l1繞l2作螺旋運動，即l1一方面繞l2作等速轉動，另一方面又沿著作等速直線運動，在運動中永遠保持與l2直交，這樣由l1所畫出的曲面叫螺旋面。

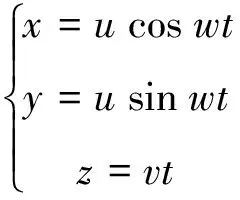
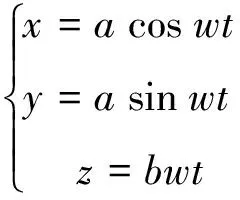
通過對問題的變形以及利用數學軟件制作動畫準確地模擬軌跡的生成過程，使學生對動點的軌跡是曲線，動直線的軌跡是曲面有了深刻的認識。

案例2：認識空間曲線關于坐標平面的射影柱面，射影柱面在認識空間曲線方面的作用、有利于空間曲線的作用。

例：畫出維維安尼曲線。

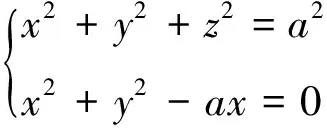
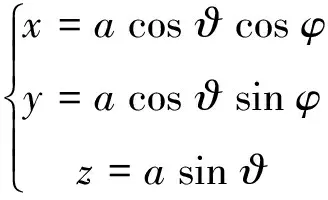
驗證性實驗的特點是直觀、動態，使深奧的解析幾何理論以圖形、動畫等形式動態地出現，達到簡單明了、直觀易懂、化難為易的教學效果。

5.2探索性實驗

數學上的概念、定理、公式的產生都是科學家們創造性思維的“結果”，是一個歸納→猜想的歸納思維過程,但教材卻表現為概念→定理或公式→范例組成的數學系統,是一個邏輯嚴密的演繹體系,教材掩蓋了這些“結果”的探索、發現、形成的復雜過程，只把思維的“結果”顯示出來。同時，傳統的教學方式也普遍地存在重結論、輕過程的現象，這種把結論、過程直接展示給學生的教學方式，使學生只記住了定理與公式，卻沒有思維活動的空間，更談不上質疑。探索實驗型教學模式打破了教材中以邏輯形式展示知識的演繹體系，從歸納的方法去學習它，就是歸納→猜想→證明的學習模式。在歸納環節中，讓學生編程序，觀察計算機的圖形演示和實驗過程，從實驗結果中分析、歸納、形成猜想，發現數學規律。現代教育理論表明，發現式的學習以問題解決為中心，學生在動手、動腦的學習活動中，通過觀察、分析、綜合、歸納、猜想等思維操作，學會解決問題和探索真理的能力。探索實驗型教學為實施發現法學習提供了很好的平臺。

在這種模式里，學生不知道“結論”的。首先教師在解析幾何教材中選擇一些概念、定理、或典型的問題設計成問題，使它與重要的知識和原理等結合在一起，從而使學生在利用數學實驗解決這類問題時，能利用到與這個問題相聯系的知識或原理去解決它。然后由學生在計算機上設計和實驗，并在這個過程中不斷嘗試、修改、完善實驗結果，并對實驗結果進行分析、猜想，最后得出“結論”，達到解決問題的目的。

案例3：用截痕曲線研究曲面形狀與性質。

柱面和錐面以它們各自的生成方式來給出定義，從定義中就可知道柱面或錐面的性質及形狀，并很容易用圖形來表示。與柱面和錐面的定義方式不同，橢球面、雙曲面和拋物面是用方程來定義的，也就是解析定義。解析定義沒有明顯的幾何特征，為了研究它們的形狀與性質，必須用平行截割法，即用一組平行平面去截割這種用方程表示的曲面，得到一族截痕曲線，通過研究這些截痕曲線的變化趨勢去推想曲面的幾何性質和整體形狀，這種推想方法抽象程度較高，學生感到難以掌握。筆者指導學生利用數學軟件(如Matlab)，在數學實驗課上自主探索曲面的形狀與性質。程序為：

(1)實驗演示

學生利用Matlab制作動畫，方法是將截痕曲線設置為逐個出現，學生容易看出曲面截痕軌跡的形成過程。

(2)分析與歸納

學生根據以平行于平面的一組平行平面所截得的一系列截痕曲線，分析這些截痕曲線的形狀變化趨勢以及它們的端點運動情況。

(3)推想與總結

案例4：演示旋轉曲面的形成過程，研究曲面性質。

在計算機上制作旋轉拋物面x2+y2=2pz的動畫演示，雖然數學軟件上沒有動畫命令，教師可引導學生制作拋物線的圖形序列。該旋轉拋物面是由yoz平面上的拋物線y=2pz繞對稱軸(z軸)旋轉而成，這種旋轉過程可以由平面曲線y2=2pz逐個出現，顯示形成動畫，直觀形象地演示了拋物線繞旋轉軸z軸旋轉而成旋轉拋物面的過程，生動地揭示了旋轉拋物面的本質。學生在實驗演示之后，總結出曲面性質。

從以上案例看到，數學實驗課程通過計算機圖形顯示、動畫模擬，形成一個形象生動的教學環境，給解析幾何教學帶來了先進的教學手段，打破了以教師為中心的滿堂灌，使教學成為“以學生為中心，教師為主導”的師生互動模式，并使學生在數學實驗中學會“提出問題、發現規律、提出猜想、進行證明”的探索與創新能力。因此數學實驗對解析幾何傳統教學方式是一種有益的補充。探討數學實驗與傳統教學如何達到優勢互補，仍是我們今后要作的進一步研究。

[1]黃文.用建構主義理論指導創造性思維方式的培養[J].廣西高教研究，1999(2).

[2]韓明，王家寶，李林.數學實驗[M].上海：同濟大學出版社，2009.

[3]許立煒.數學實驗課程中的實驗設計原則[J].大學數學，2010(8).

[4]陳曉瑛，龔日超.國內外數學實驗教學的現狀分析與展望[J].株洲師范高等專科學校學報，2004(10).

[5]李繼成，朱旭，王綿森，等.數學實驗課程建設及分層次教學與實踐[J].大學數學，2005(12).

(責任編輯：高 堅)

On Teaching Design for Mathematical ExperimentalCourse on Analytic Geometry

Shi Xiangdong

(College of Information and Electronic Engineering, Wuzhou University, Wuzhou 543002, China)

Mathematical experimental teaching and learning based on the natures of knowledge, practice and operation and integrated with computer systems is a new mathematical course which is helpful for the improvement of students’ innovation ability and comprehensive quality. Based on the characteristics of analytic geometry, this paper puts forward some principles for teaching design of mathematical experimental course and some approaches to course arrangement.

Analytic geometry; Mathematical experiment; Teaching design; Mathematical software

2016-04-01

梧州學院教學改革項目(Wyjg2014B011)

G642.4

A

1673-8535(2016)03-0063-06

石向東(1961-)，男，廣西梧州人，梧州學院副教授，主要研究方向：微分方程。