安全通論(9)
——紅客篇

楊義先，鈕心忻

(北京郵電大學 信息安全中心，北京 100876)

?

安全通論(9)
——紅客篇

楊義先，鈕心忻

(北京郵電大學 信息安全中心，北京 100876)

編者按：文章揭示了紅客的本質，即，維護系統的“安全熵”值，避免其突變，當然，如果能夠“使熵減少或不增”就最理想。通過對熵的時變微分方程的討論，分析了各種情況下，系統的安全態勢以及紅客的業績評價等。我們過去一直認為，網絡安全對抗的狀態只有兩個：此起、彼伏，或者說是“水漲”、“船高”，但卻忽略了另一個更重要的狀態，即納什均衡！那時，攻防雙方的最佳策略都是“靜止不動”，至少表面上是這樣。

0 引言

紅客是被黑客逼出來的，沒有黑客就不需要紅客。但遺憾的是，黑客不但沒有絕跡，而且還越來越多，越來越兇！

在某種意義上，黑客代表“邪惡”，因此，黑客的行動都是在隱蔽環境下進行的，不敢對外公開。從而，黑客獲勝的主要法寶就是技術和其他“雞鳴狗盜”。

楊義先

教授，博士生導師，災備技術國家工程實驗室主任，北京郵電大學信息安全中心主任，教育部網絡攻防重點實驗室主任，《微型機與應用》編委，主要研究方向：網絡空間安全、現代密碼學和糾錯編碼等。

鈕心忻

博士，教授，博士生導師。北京郵電大學學士和碩士學位，香港中文大學電子工程系博士學位。1997年起在北京郵電大學信息工程學院(現計算機學院)從事教學與科研工作。主要研究方向：網絡與信息安全、信號與信息處理等。

在某種意義上，紅客代表“正義”，因此，紅客的行動都是公開的，他們可以光明正大地運用包括法律、法規、標準、管理、技術、教育等一切手段來捍衛系統的安全。

從表面上看，紅客的行動包括(但不限于)安裝防火墻、殺病毒、抓黑客、加解密、漏洞掃描、制定標準、頒布(或協助頒布)相關法律法規，而且還經常刪貼、封網、雇水軍等。但是，這些都是錯覺，如果要單一地考慮紅客的這些防衛措施，那么，《安全通論》將無立足之地，而且系統的安全防守工作將越來越亂。過去，也許因為沒有搞清紅客的本質，所以，紅客才做了許多事倍功半的事情，甚至還做了不少負功，既沒有能擋住黑客的攻擊，又把自己的陣營搞得一團糟，甚至逼反了自己的“友軍”。其實，紅客的本意，是只想做一件事，那就是：維護系統的熵(或秩序)！或更準確地說，最好能夠“減少系統的熵”，次之是要“阻止系統的熵被增大”，至少要確保“系統的熵不要過快地增大”。因此，能夠維護好熵的紅客，才是合格的紅客；否則，就是差紅客，甚至是幫倒忙的紅客。

過去一直認為，網絡安全對抗的狀態只有兩個：此起、彼伏(或者說是“水漲”、“船高”)，但卻忽略了另一個更重要的狀態：納什均衡！那時，攻防雙方的最佳策略，都是“靜止不動”，至少表面上是這樣。

由于紅客可以使用黑客的所有技術，所以，本文不再重復文獻[1-8]中提到過的所有技術部分，而是充分運用《系統論》[9]來揭示紅客的本質。

1 安全熵及其時變性研究

考慮由紅客、黑客、用戶、網絡和服務等組成的系統。由“熱力學第二定律”可知該系統的熵(或秩序，或組織性)一定會隨著時間的流逝而不斷地自動增大，這意味著“系統的不安全性”也在不斷地增大。特別是黑客的存在，使得這種“熵增大”的趨勢更明顯，因為，黑客的實質就是搞破壞，就是要搞亂系統的既定秩序；而與之相反，紅客的目的就是要有效阻止這種系統崩析(耗散)趨勢，確保用戶能夠按既定的秩序在系統中提供或獲得服務。當然，用戶的誤操作(或者紅客的亂操作)也會在實際上搞亂系統，增大系統的熵。不過，為了清晰起見，本文不考慮諸如用戶誤操作、紅客和黑客失誤等無意行為所造成的亂序問題。

由于有紅客、黑客等人為因素的影響，所以，網絡系統顯然不是“封閉系統”(如果只考慮設備，那么，系統就可看成是“封閉系統”，實際上，它還是一個“有限系統”)，更由于紅客和黑客連續不斷的攻防對抗，使得系統熵(秩序的度量)不斷地被增大和縮小，即系統的熵始終是時變的。

設系統的全部不安全因素為q1,q2,…,qn，記t時刻系統的熵為Q(t,q1,q2,…,qn)，或者簡記為Q(t)。當Q(t)=0時，系統的熵達到最小值，此時系統的安全性就達到最大值(因為根據文獻[1]，“安全”是“負熵”，或者說“不安全”是“熵”)。當然，一般情況下，熵總是正數。若Q(t)隨時間而增長，即微分dQ(t)/dt>0，那么，系統將變得越來越不安全；反之，若Q(t)隨時間而減少，即微分dQ(t)/dt<0，那么，系統將變得越來越安全。因此，以下將Q(t)稱為“安全熵”。而紅客的目標就是要努力使得“安全熵”越來越小，黑客則想使“安全熵”越來越大。

對每個i(i=1,2,…,n)，記Q(t,qi)(更簡單地記為Qi(t)或Qi)為在“只存在不安全因素qi”的條件下，在t時刻，系統的“安全熵”。那么，各個Qi(t)的時變情況便可以用方程組(1)來描述：

(1)

這里，任何一個Qi的變化都是所有其他各Qj(j≠i)的函數；反過來，任一Qi的變化也承擔著所有其他量和整個方程組(1)的變化。

下面針對一些特殊情況來仔細討論方程組(1)。

如果各個Qi不隨時間而變化，即，dQi/dt=0，i=1,2,…,n(或者說f1(Q1,Q2,…,Qn)=f2(Q1,Q2,…,Qn)=…= fn(Q1,Q2,…,Qn)=0)，那么，此時系統的“安全熵”就處于靜止狀態，即系統的安全性既不變壞，也沒有變得更好。如果從系統剛剛投入運行開始(即t=0)，紅客就能夠維護系統，使其“安全熵”永遠處于靜止狀態，那么，這樣的紅客就是成功的紅客！

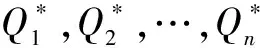
(2)

如果這個方程組可以展開為泰勒級數，即得到如下方程組(3)：

(3)

該方程組的通解是：

(4)

此處各個G都是常數，λ(i),i=1,2,…,n，則是如下n×n階矩陣B=[bij]的行列式關于λ的特征方程的根，即方程det(B)=0的根，這里B=[bij]，bii=aii-λ,i=1,2,…,n，而當i≠j時，bij=aij。

上述特征方程的根λ(i)既可能是實數，也可能是虛數。下面考慮幾種特別情況：

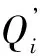
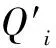
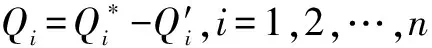
(3)如果有一個特征根λ(i)是正數或0，那么，系統的平衡就不穩定了，即系統的安全性也不穩定了，紅客就有可能失控。

(4)如果有一些特征根λ(i)是正數和復數，那么，系統中就包含著周期項，因為，指數為復數的指數函數具有這樣的形式：

e(a-ib)t=eat[cos(bt)-isin(bt)]

這里i為虛數單位。

此時，系統的安全狀態會出現周期性的振動，即會出現紅客與黑客之間的反復“拉鋸戰”，雖然雙方會各有勝負，但是，總體趨勢是向著對紅客不利的混亂和不安全方向發展。

為了使上面的討論更加形象，現在考慮n=2，即此時系統的不安全因素主要有兩個(比如“黑客攻擊”和“用戶操作失誤”這兩個宏觀的因素)，那么方程組(1)就簡化為：

dQ1/dt=f1(Q1,Q2)和dQ2/dt=f2(Q1,Q2)

在可以展開為泰勒級數的假設下，它的解為：

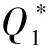
λ=C/2±√[-D+C2/4]

其中，C=a11+a22, D=a11a22-a12a21，√表示平方根。

于是，可知：

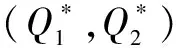
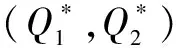
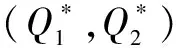
(4)若C>0，D>0，E>0，那么，特征方程的兩個解都是正數，此時，完全不存在靜態，或者說，此時系統更混亂，紅客完全失控，只能眼睜睜地看著系統最終崩潰！

更進一步，下面再來考慮n=1這種最簡單的情況，此時，系統的不安全因素只有一個(比如黑客的破壞)。于是，方程組(1)就簡化為方程：dQ/dt=f(Q)。若將f(Q)展開為泰勒級數，那么，就得到如下方程：

dQ/dt=a1Q+a11Q2+…

此泰勒式中未包含常數項，因為，我們可以假定：“不安全因素”不會自然發生，即，系統剛剛被使用(t=0)的那一刻，系統不會出現安全問題。

如果粗略地只保留該泰勒級數中的第一項，那就有dQ/dt=a1Q，這說明：系統的安全態勢將完全取決于常數a1是正還是負。如果a1為負，那么“安全熵”整體上向減少的方向發展，即系統的安全性會越來越好，對紅客有利；如果a1為正，那么“安全熵”整體上向增加的方向發展，即系統的安全性會越來越差，對紅客不利。而且，系統的這種越來越安全(或越來越不安全)的態勢遵從指數定律：Q=Q0ea(1)t，其中，Q0表示初始時刻(t=0)時系統的“安全熵”；而a(1)是a1的等價表達式，這主要是為了簡化公式中足標體系的復雜度(這是因為Q=Q0ea(1)t是方程dQ/dt=a1Q的解)。該指數定律表明：如果系統的安全態勢在向好的方面發展，那么，變好的速度會越來越快；反之，如果系統的安全態勢在向壞的方面發展，那么，變壞的速度也會越來越快，甚至瞬間崩潰！

如果再精細一點，即，保留上述泰勒級數的前兩項，于是，就有方程：

dQ/dt=a1Q+a11Q2

該方程的解為Q=[a1cea(1)t]/[1-a11cea(1)t]。注意，隨著時間的延伸，該解所畫出的曲線就是所謂的“對數曲線”，它是一個趨向于某極限的S形曲線，也就是說，此時，從安全性角度來看，系統的變好和變壞，還是有“底線”的。

下面，我們再換一個角度來看系統安全，即，跳出系統，完全以旁觀的第三方身份來看紅客與黑客之間如何“道高一尺魔高一丈”地“水漲船高”。

此時，影響系統安全性的因素只有兩個(即，紅客努力使系統變得更安全，使“安全熵”不增；而黑客卻努力要使系統不安全，增加“安全熵”)，而且，假如這兩個因素之間還是相互獨立的，即，各方都埋頭于自己的“攻”或“守”，或者說，紅客(黑客)的“安全熵”隨時間變化的情況與黑客(紅客)的“安全熵”無關，而且還只考慮“主要矛盾”，即，此時在方程組(3)中，每個方程式只保留第1項，其他系數都為0。于是，方程組(3)被簡化為：

(5)

解此方程組，可得其解為：Q1=c1ea(1)t和Q2=c2ea(2)t，從中再解出時間t，可得：t=[lnQ1-lnc1]/a1=[lnQ2-lnc2]/a2。設a=a1/a2，b=c1/(c2)a，那么就有如下重要公式：

Q1=b(Q2)a

它說明紅客與黑客的“安全熵”(Q1和Q2)彼此之間是冪函數關系，比如，紅客維護系統安全所貢獻的“安全熵”是黑客破壞系統安全所增大“安全熵”的冪函數。為更清楚起見，將上面式(5)重寫如下：

{[dQ1/dt][1/Q1]}:{[dQ2/dt][1/Q2]}=a或者dQ1/dt=a(Q1/Q2)(dQ2/dt)

這里，前一部分說明：在只考慮紅客和黑客的“安全熵”(Q1和Q2)的前提下，紅客使其“安全熵”的相對增長率([dQ1/dt][1/Q1])與黑客的“安全熵”的相對增長率([dQ2/dt][1/Q2])之間的比值竟然是常數！而后一部分，更出人意料地表示：紅客“安全熵”的時變率(dQ1/dt)與黑客“安全熵”的時變率(dQ2/dt)之間的關系，竟然是如此簡潔！

若a1>a2，即紅客“安全熵”Q1的增長率大于黑客“安全熵”Q2的增長率，那么，a=a1/a2>1，它表明紅客對系統整體安全性走勢的掌控力更強；反過來，若a1

再考慮泰勒級數方程組(3)的另一種情況：各個不安全因素彼此之間相互獨立(比如，由文獻[1]可知，當這些不安全因素就是系統安全“經絡圖”中的全體“元誘因”時，這些不安全因素之間就是相互獨立的)，此時，方程組(3)就簡化為：

dQi/dt=ai1Qi+ai11(Qi)2+ai111(Qi)3+…

此時，不安全因素對系統“安全熵”的整體影響，就等于每個不安全因素對系統“安全熵”各自影響的累加，即此時有“整體等于部分和”。

方程組(3)還有一種特殊情況值得單獨說明，即假如有某個不安全因素qs的泰勒展開式系數在各個方程中都很大，而其他不安全因素的泰勒系數卻很小甚至為0，那么，不安全因素qs就是不安全因素的主導部分，系統的不安全性可能主要是由它而引發，因此，這樣的不安全因素qs就應該是紅客關注的重點，要盡力避免它成為系統崩潰的“導火索”。2 結束語

雖然紅客與黑客在技術方面幾乎沒有區別，甚至他們的技術可以彼此通用，但是，作為系統安全的正、反兩種力量的代表，他們在角色方面的差別還是很大的，因此，值得專門設立篇幅來進行研究。

如果說黑客的手段雜亂無章，那么，紅客的手段更是一團亂麻(甚至紅客還會“好心辦壞事”，即做一些本該黑客搞的破壞)，如何找到一條線索來把“這團亂麻”理清，這是一個嚴峻的挑戰。幸好我們偶然從文獻[1-8]中發現了一個總是伴隨著《安全通論》的“幽靈”，即“熵”，而且，運氣更好的是，經過分析，“熵”竟然與紅客的本質密不可分，而且還是解開“亂麻”的重要線索。貝塔朗菲的《一般系統論》[9]對系統熵進行了恰到好處的研究，因此，被本文深度參考。文中的許多思路和方法都依賴于“系統論”，只不過貝塔朗菲用它們去研究生物的新陳代謝系統，而本文用它們來研究網絡系統；貝塔朗菲研究的是生物熵，而此處研究的是“安全熵”而已。

本文揭示了紅客的實質是“維護系統的安全熵”，并詳細分析了系統“安全熵”的多種情況下的時變特性。但是，到底應該怎樣做才能夠有效地阻止“安全熵”變大的趨勢？這當然是一個重要而又困難的問題，過去全球安全界的同行們做了許多“埋頭拉車”的具體工作，但是，在“抬頭看路”方面還真的做得不夠，比如：

(1)都說安全是“三分技術，七分管理”，但是，真正落實到行動上時，大家在“安全管理”方面花費的精力遠遠未達到“七分”。因此，我們希望能夠在《安全通論》中，專門開辟“管理篇”來詳細研究“如何用管理的辦法來維護系統的安全熵”；

(2)及時反饋也是紅客維護“安全熵”并在必要時對其進行微調的重要辦法，因此，維納的《控制論》在《安全通論》中也應該有特殊的地位，但是，突破口確實很難找。

對紅客的研究肯定不僅僅限于本文的這些內容，但是，為了盡快搭建起《安全通論》的核心骨架，吸引全球盡可能多的安全專家來一起“挖金礦”，我們不得不先放棄一些細節，比如，其實開放系統的“安全熵”永遠不會處于平衡狀態，而是會維持在所謂的“穩態”上，這與有機體的新陳代謝相同，而且，同樣具有“異因同果性”，即，由不同的原因導致相同的結果，比如，或者是因為“黑客太弱”，或者是因為“紅客太強”，而使得系統的安全無恙；反過來，或者是因為“黑客太強”，或者是因為“紅客做了負功”，而使得系統崩潰。系統一旦達到“穩態”，就必定表現出“異因同果性”。

[1] 楊義先，鈕心忻.安全通論(1)——經絡篇[J].微型機與應用，2016，35(15)：1-4.

[2] 楊義先，鈕心忻.安全通論(2)——攻防篇之“盲對抗”[J].微型機與應用，2016，35(16)：1-5.

[3] 楊義先，鈕心忻，安全通論(3)——攻防篇之“非盲對抗”之“石頭剪刀布”[J].微型機與應用，2016，35：(17)1-3.

[4] 楊義先，鈕心忻，安全通論(4)——攻防篇之“非盲對抗”之“童趣游戲”[J].微型機與應用，2016，35(18)：3-5，9.

[5] 楊義先，鈕心忻，安全通論(5)——攻防篇之“非盲對抗”之“勸酒令”[J].微型機與應用，2016，35(19)：2-6.

[6] 楊義先，鈕心忻，安全通論(6)——攻防篇之“多人盲對抗”[J].微型機與應用，2016，35(20)：1-4.

[7] 楊義先，鈕心忻，安全通論(7)——黑客篇之“戰術研究”[J].微型機與應用，2016，35(21)：1-4.

[8] 楊義先，鈕心忻，安全通論(8)——黑客篇之“戰略研究”[J].微型機與應用，2016，35(22)：1-5.

[9] 馮·貝塔朗菲.一般系統論：基礎、發展和應用(第1版)[M].林康義，魏宏森，等，譯.北京：清華大學出版社，1987.

(本文轉自楊義先教授科學網博客，鏈接地址：http://blog.sciencenet.cn/blog-453322-960372.html。本系列完，更多《安全通論》相關內容請關注楊義先教授科學網博客)