一種新的結(jié)合NSCT和PCNN的圖像融合方法*
楊 丹,何建農(nóng)
(福州大學 數(shù)學與計算機科學學院,福建 福州 350116)
?
一種新的結(jié)合NSCT和PCNN的圖像融合方法*
楊 丹,何建農(nóng)
(福州大學 數(shù)學與計算機科學學院,福建 福州 350116)
考慮到小波變換存在一些局限性,提出一種把非下采樣Contourlet變換(NSCT)與脈沖耦合神經(jīng)網(wǎng)絡(PCNN)相結(jié)合的圖像融合新方法。用NSCT變換從多尺度和多方向上分解配準后的原始圖像。低頻應用改進的邊緣能量結(jié)合空間頻率的融合方法;高頻應用PCNN簡化數(shù)學模型,其鏈接強度用改進的拉普拉斯能量和表示。并且選擇點火映射圖的點火次數(shù)與其標準差相結(jié)合的方法。最后經(jīng)過NSCT逆變換得出融合圖像。實驗分析可知,與其他幾種圖像融合方法進行比較,新方法取得了更高質(zhì)量的融合圖像。
圖像融合;非下采樣輪廓波變換;脈沖耦合神經(jīng)網(wǎng)絡;邊緣能量;拉普拉斯能量和
0 引言
圖像融合是將由不同傳感器獲得的圖像的重要信息進行互相補充,得到一幅含有更加全面信息的新圖像,它能夠更加準確地描述真實場景[1]。比較經(jīng)典的是小波變換方法,不過它只有點奇異性,而且方向受到限制,因此不能解決高維問題。為了打破方向上的限制,相關學者又研究出了一些新方法,如Contourlet變換,它比小波變換處理的效果好,但其沒有平移不變性。所以,CUNHA A L等[2]對Contourlet變換作了改進,提出非下采樣Contourlet變換(Nonsubsanpled Contourlet Transform,NSCT),它有平移不變的性質(zhì)。脈沖耦合神經(jīng)網(wǎng)絡(Pulse-Coupled Neural Network,PCNN)是Eckhorn提出來的,它對圖像融合領域產(chǎn)生了重要影響。
1 NSCT變換
NSCT變換是由兩個重要的部分構(gòu)成,它們分別為非下采樣金字塔濾波器組(NSP)和非下采樣方向濾波器組(NSDFB)[3]。用NSP從多尺度上分解輸入圖像,獲得低頻子帶、高頻子帶;用NSDFB從多方向上分解高頻子帶,獲得方向子帶。重復進行這兩個操作就是對圖像進行了NSCT變換。NSCT變換的工作流程中不包含上采樣和下采樣的環(huán)節(jié),因而擁有平移不變的性質(zhì),這是它與Contourlet變換的重要區(qū)別。圖1為NSCT的結(jié)構(gòu)示意圖。
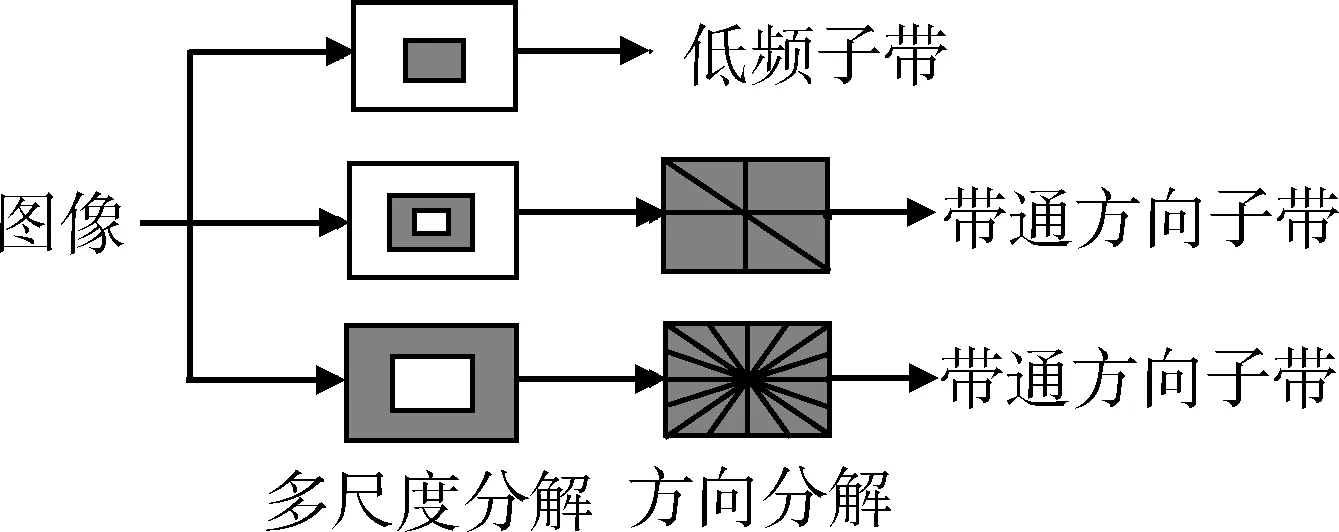
圖1 NSCT結(jié)構(gòu)示意圖
2 NSCT與PCNN相結(jié)合的圖像融合方法
2.1 融合步驟
本文提出一種NSCT與PCNN相結(jié)合的新算法。具體步驟如下:
(1)利用NSCT變換分解原圖像A與B,獲得高低頻系數(shù)。
(2)低頻使用的是改進的邊緣能量與空間頻率相結(jié)合的融合策略;高頻引入PCNN模型,其鏈接強度使用的是改進的拉普拉斯能量和,選擇點火映射圖的點火次數(shù)與其標準差相結(jié)合的融合策略。
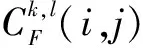
2.2 低頻融合規(guī)則
利用NSCT分解之后的低頻域表示圖像的大體輪廓,它是對真實場景的近似描述。因為空間頻率可以表征圖像的活躍狀態(tài),邊緣區(qū)域能量能夠反映其邊緣特征。參考文獻[4]和[5]使用邊緣能量與空間頻率相結(jié)合的融合策略,能夠有效地保留圖像的邊緣細節(jié)信息,提高圖像的清晰度。改進的邊緣能量定義:
(1)
EDJ(i,j)=(L1*CJ)2(i,j)+(L2*CJ)2(i,j)+
(L3*CJ)2(i,j)
(2)
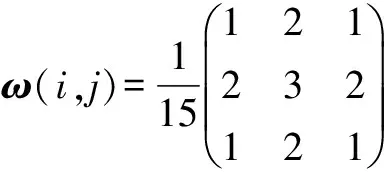
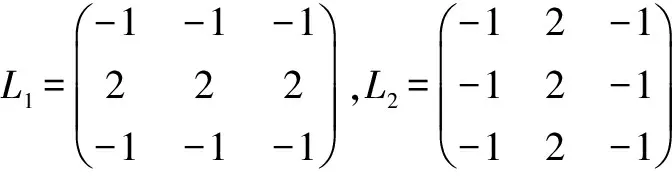
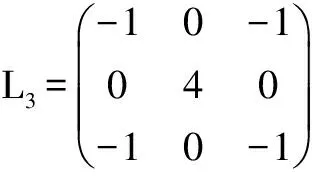
其中,EJ(i,j)為原始圖像J在像素(i,j)處的邊緣能量,J=A、B;CJ表示圖像的低頻系數(shù);*表示卷積。
改進的空間頻率定義為:
(3)
式(3)中,
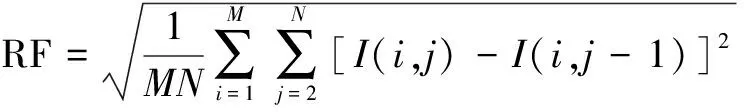
(4)
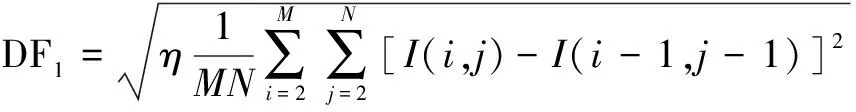
(5)
其中,SF為空間頻率;RF、CF分別表示行頻率和列頻率;DF1、DF2分別表示對角線為45°和135°時的頻率;I(i,j)為像素(i,j)處的灰度值;η=0.707。
加權系數(shù)是通過對S函數(shù)[6]改進得到的,本文改進的S函數(shù)為:
(6)
式(6)中,
(7)
其中,?為收縮因子,本文取為5。
最終獲得的融合系數(shù)為:
CF(i,j)=
(8)
當EA(i,j)SFA(i,j)=EB(i,j)SFB(i,j)時,CF(i,j)=a(i,j)CA(i,j)+b(i,j)CB(i,j)
(9)
其中,加權系數(shù)a(i,j)=w(i,j),b(i,j)=1-a(i,j);CF(i,j)為融合圖像F在像素(i,j)處的低頻融合系數(shù)。
2.3 高頻融合規(guī)則
PCNN是由一些神經(jīng)元組合成的網(wǎng)絡,每個神經(jīng)元都是由接受域、調(diào)制部分和脈沖產(chǎn)生器三個成分動態(tài)非線性地構(gòu)成[7]。本文使用的是PCNN的簡化模型,其數(shù)學模型如式(10)所示:
(10)
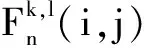
高頻系數(shù)表示的是圖像的細節(jié)紋理信息,人的視覺更傾向于對這部分信息的關注。考慮到PCNN方法能夠更好地提取圖像的細節(jié)信息,所以本文在處理高頻方面引入PCNN模型。參考文獻[8]及[9],在PCNN的模型中,其刺激輸入采用高頻系數(shù),鏈接強度采用改進的拉普拉斯能量和,融合規(guī)則選取點火次數(shù)與其標準差相結(jié)合的方法。此方法能夠更加充分地展現(xiàn)圖像的細節(jié)紋理特征。改進的拉普拉斯能量和的定義:
(11)
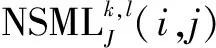
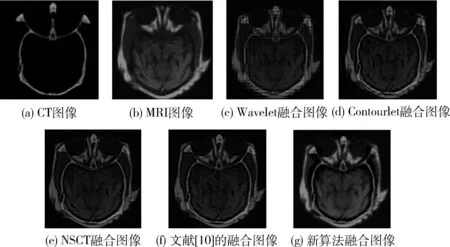
圖2 醫(yī)學圖像的融合結(jié)果

圖3 多聚焦圖像融合結(jié)果
計算點火映射圖的標準差為:
(12)
式(12)中,
(13)
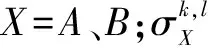
本文選擇PCNN的點火映射圖的點火次數(shù)與其標準差相結(jié)合的融合方法:
(14)
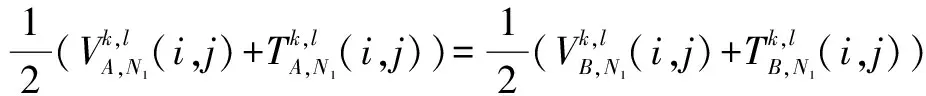
(15)
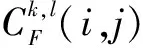
3 仿真實驗結(jié)果和分析
本文選擇了兩組精確配準后的多聚焦圖像和醫(yī)學圖像進行分析。通過用新算法與其他4種算法進行比較,證明新算法的有效性。其他4種算法分別為:小波變換算法(WT)采用低頻取平均,高頻取大的融合方法;Contourlet變換算法中低頻采用取平均,高頻能量取大;NSCT算法采取低頻取平均,高頻采取絕對值取較大者的方法;文獻[10]中低頻選擇加權平均,高頻引入PCNN,其鏈接強度為拉普拉斯能量和。
從人眼視覺上對兩組圖像分別進行分析。觀察圖2,圖2(c)出現(xiàn)明顯的頻譜失真現(xiàn)象,整體比較模糊。圖2(d)效果有所改善,但是骨骼、軟組織等信息損失較為嚴重。圖2(e)和(f)清晰度有所提高,但是具體細節(jié)紋理信息不夠清晰,圖(f)比(e)的效果好些。圖2(g)為新方法的結(jié)果,圖中的骨骼結(jié)構(gòu)、軟組織部分很清楚,亮度合適,有利于人眼觀察。
觀察圖3,圖3(c)中右邊的條形碼出現(xiàn)失真現(xiàn)象,圖中的字跡很模糊。圖3(d)比前者清晰,但是邊緣出現(xiàn)虛影。圖3(e)和(f)的效果有所改善,但是圖中的字跡不夠光滑。圖3(g)為新算法的結(jié)果,圖中的所有字跡都很光滑、清楚,能夠看出條形碼的細節(jié)紋理。
本文還使用了4個客觀指標進行評價。空間頻率(SF)表示圖像的空間活躍狀態(tài),數(shù)值越大其清晰度越高。標準差(STD)表示圖像的對比度,取值越大其對比度越高。信息熵(IE)是反映圖像保留下來的信息量的多少。QAB/F是表征邊緣信息的指標,取值越靠近1表明其效果越好。對表1和表2進行分析可知,本文所提出的算法在這4個評價指標上都比其他4種方法的數(shù)值大,由此證明新算法所得到的融合圖像效果是最好的。
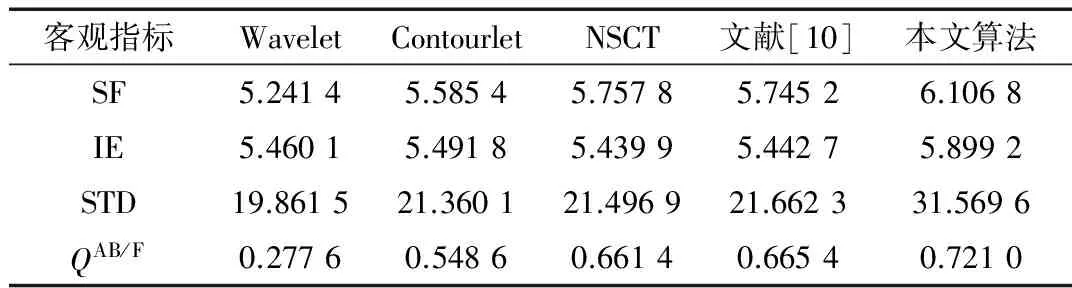
表1 醫(yī)學圖像融合算法的評價表
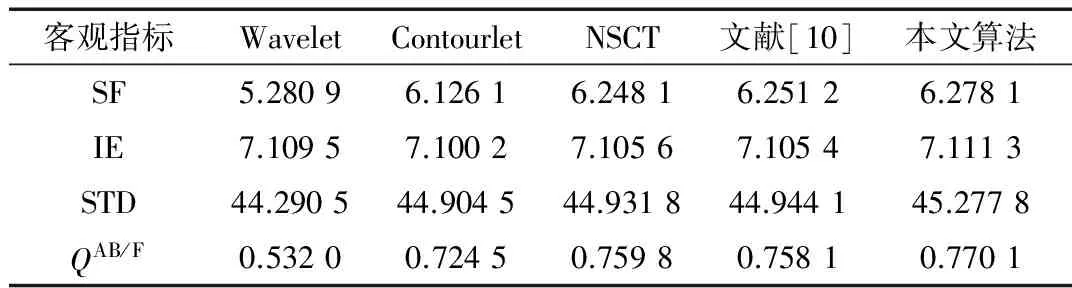
表2 多聚焦圖像融合算法的評價表
4 結(jié)束語
綜合NSCT變換與PCNN的優(yōu)點,本文采取把兩者相結(jié)合的圖像融合新算法。本文的關鍵之處是對高低頻融合方法的改進。低頻應用改進的邊緣能量與空間頻率相結(jié)合的融合方法,高頻應用PCNN模型,其鏈接強度為改進的拉普拉斯能量和。并且通過點火映射圖的點火次數(shù)與其標準差相結(jié)合的方法選擇高頻融合系數(shù)。最后,對融合結(jié)果進行主觀與客觀評價,充分驗證了新算法的有效性與可靠性。
[1] 周渝人, 耿愛輝, 王瑩,等. 基于對比度增強的紅外與可見光圖像融合[J]. 中國激光, 2014,41(9):223-229.
[2] CUNHA A L Da ,ZHOU J P ,DO M N. Nonsubsampled contourlet transform:theory,design, and applications [J].IEEE Transactions on Image Processing,2006,15(10):3089-3101.
[3] 李美麗, 李言俊, 王紅梅,等. 基于NSCT和PCNN的紅外與可見光圖像融合方法[J]. 光電工程, 2010, 37(6):90-95.
[4] WANG J, LI Q, JIA Z, et al. A novel multi-focus image fusion method using PCNN in nonsubsampled contourlet transform domain[J]. Optik - International Journal for Light and Electron Optics, 2015, 126(20):2508-2511.
[5] 鄭偉, 孫雪青, 李哲. shearlet變換和區(qū)域特性相結(jié)合的圖像融合[J]. 激光技術, 2015,39(1):50-56.
[6] 劉衛(wèi), 殷明, 欒靜,等. 基于平移不變剪切波變換域圖像融合算法[J]. 光子學報, 2013, 42(4):496-503.
[7] WANG Z B,MA Y D,CHENG F Y,et al.Review of pulse-coupled neural networks[J].Image and Vision Computing,2010,28(1):5-13.
[8] 李新娥, 任建岳, 呂增明,等. NSCT域內(nèi)基于改進PCNN和區(qū)域能量的多光譜和全色圖像融合方法[J]. 紅外與激光工程, 2013, 42(11):3096-3102.
[9] CHAI Y, LI H, ZHANG X. Multifocus image fusion based on features contrast of multiscale products in nonsubsampled contourlet transform domain[J]. Optik - International Journal for Light and Electron Optics, 2012, 123(7):569-581.
[10] 姜志.基于PCNN和NSCT變換的圖像融合算法研究[D].杭州:浙江理工大學,2014.
A novel image fusion method based on NSCT and PCNN
Yang Dan, He Jiannong
(College of Mathematics and Computer Science,Fuzhou University,Fuzhou 350116,China)
Considering the wavelet transform has some limitations, a novel image fusion method based on the combination of Nonsubsampled Contourlet Transform(NSCT) and Pulse Coupled Neural Networks(PCNN) is proposed. Firstly,the registered original images are decomposed at multi-scale and multi-direction by NSCT. Then, the fusion method combing improved edge energy with spatial frequency is used in the low frequency part.Simplified mathematical model of PCNN is used in the high frequency part.Improved sum of Laplaceenergy is used as linking strength of PCNN.The high frequency fusion coefficients are acquired by the method of combing the fire numbers with the standard deviation of the fire mapping images.Finally, the fusion image is obtained by inverse NSCT.The experimental analysis show that the novel method has higher quality fusion image than the other several methods.
image fusion;Nonsubsampled Contourlet Transform (NSCT);Pulse-Coupled Neural Network (PCNN);edge energy;the sum of Laplace energy
國家自然科學基金項目(51277032)
TP391
A
10.19358/j.issn.1674- 7720.2016.23.013
楊丹,何建農(nóng). 一種新的結(jié)合NSCT和PCNN的圖像融合方法[J].微型機與應用,2016,35(23):46-48,55.
2016-09-06)
楊丹(1989-),女,碩士研究生,主要研究方向:智能圖像處理。
何建農(nóng)(1960-),通訊作者,女,學士,副教授,碩士生導師,主要研究方向:智能圖像處理、網(wǎng)絡GIS、信息安全。E-mail:42566374@qq.com。

