關于對偶Steiner多項式的根的注記

張德燕，馬統一

（1.淮北師范大學數學科學學院，安徽淮北235000；2.同濟大學數學系，上海200092；3.河西學院數學與統計學院，甘肅張掖734000）

關于對偶Steiner多項式的根的注記

張德燕1，2，馬統一3

（1.淮北師范大學數學科學學院，安徽淮北235000；2.同濟大學數學系，上海200092；3.河西學院數學與統計學院，甘肅張掖734000）

受凸體的Steiner多項式的啟發，定義了星體的對偶Steiner多項式，并利用對偶Aleksandrov-Fenchel不等式討論了對偶Steiner多項式的根.進而，得到了關于對偶Steiner多項式的根的一些不等式，這些不等式恰好是關于Steiner多項式的根的不等式的對偶形式.

Steiner多項式；對偶Steiner多項式；對偶Aleksandrov-Fenchel不等式

1 引言

記Kn是所有凸體（n維歐氏空間Rn中的緊凸集）的集合，Bn是n維單位球體，Kno表示所有有非空內部的凸體的集合，則Kno?Kn.我們用V（·）表示n維體積.對任意的凸體K，E∈Kn，ρ是一個非負實數，則V（K+ρE）可以表示成ρ的n次多項式：

若E=Bn，（1.1）式是經典的Steiner公式［2］，Wi（K；Bn）通常簡記為Wi（K），是經典的第i階均值積分.

一般地，凸體K關于E的相對內半徑r（K；E）和相對外半徑R（K；E）定義為：

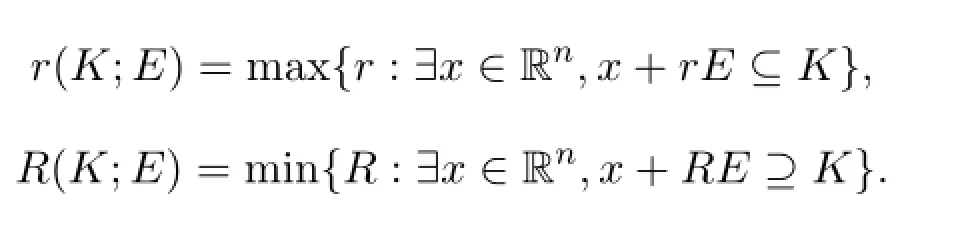
定義1.1［3］記C為復數域.設s∈C，稱關于變量s的多項式

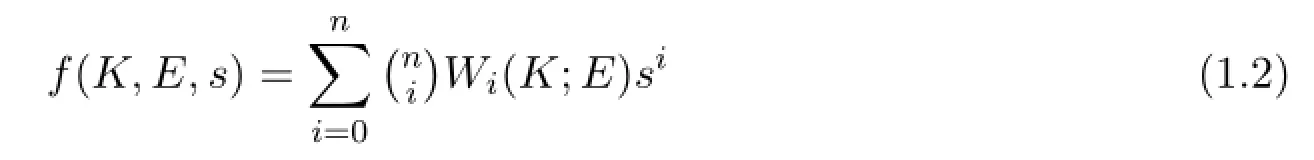
為（相對）Steiner多項式.

在Brunn-Minkowski理論中，Steiner多項式是一個重要的研究課題，尤其是對Steiner多項式根的討論已受廣泛關注［37］.當n=2時，Steiner多項式有兩個負實根，其中一個不大于-R（K；E），另一個不小于-r（K；E）.在文獻［8］中Teissier提出是否可將此結果推廣到n＞2的情形？同時文獻［7，9］中提出了下面的猜想：

猜想記Re（s）為一個復數s的實部.設K，E∈Kn，γi（i=1，···，n）是Steiner多項式f（K，E，s）的n個根，且滿足Re（γ1）≤···≤Re（γn），則

上面已經提到n=2時該猜想正確.對n=3的情形，文獻［5］中已經證明對于一些特殊的凸體該猜想正確.對任意維數n，文獻［3］中證明了：設K∈Kn，E∈Kno，γi（i=1，···，n）是Steiner多項式f（K，E，s）的n個根，則

（i）若K是m維的且m≥1，則非零根γi滿足

其中上界是最優的，且r（K；E）/n≤|γi|≤nR（K；E）.

（ii）|Re（γ1）|+···+|Re（γn）|≥nr（K；E）.

（iii）若Re（γi）≤0，i=1，···，n，則

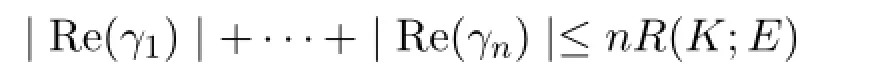
相比較凸體理論，它的對偶理論即星體理論在凸幾何中也扮演著重要的角色.在本文中我們對星體K，E定義對偶Steiner多項式g（K，E，s）：

在第三節中將討論對偶Steiner多項式g（K，E，s）的根，并利用對偶的Aleksandrov-Fenchel不等式［10］得到了與對偶Steiner多項式的根有關的不等式，見本文的定理3.1，它恰好是上面提到的文獻［3］中的結論（i）-（iii）的對偶形式.

2 準備工作及引理

記Sn-1是Rn中的單位球面.設Rn中的一個緊子集K關于原點是星形的，它的徑向函數ρK=ρK（·）：Rn｛0｝→R定義為

若ρK是正定的連續的，則K叫做一個關于原點的星體（簡稱星體）.用Sn記作Rn中全體星體的集合.

設K∈Sn，c是一個實數，則Minkowski數乘cK定義為

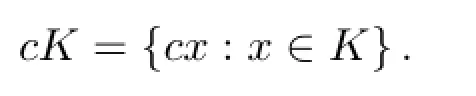
從徑向函數的定義不難得到：若K是一個星體，c≥0，則

我們稱兩個星體K，L是互為膨脹的，若ρK（u）/ρL（u）是與u∈Sn-1無關的常數.

對于α，β≥0，星體K，L的徑向線性組合［10］定義為

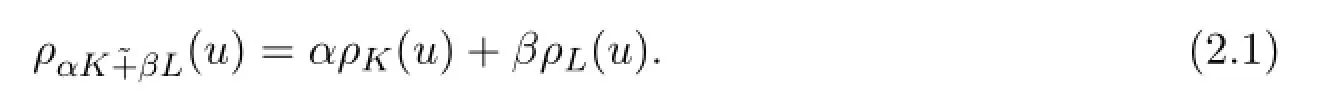
若Kj∈Sn（1≤j≤n），對偶混合體積［10］定義為

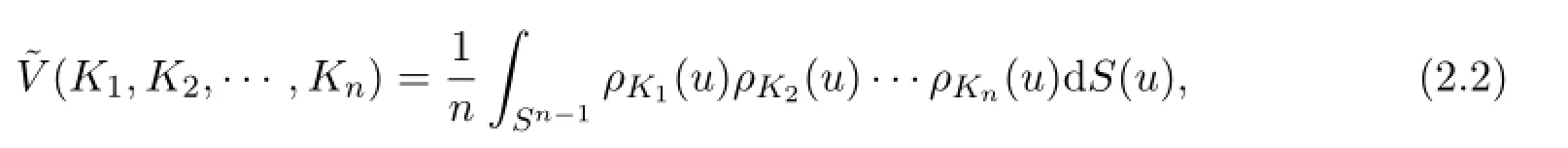
其中dS（u）是Sn-1上的n-1維體積元.設s，t是兩個和不超過n的非負整數，K，L是兩個星體，是n-s-t個星體的星體組（C1，···，Cn-s-t）.記是對偶混合體積

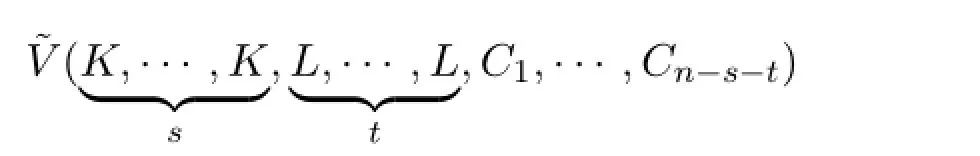
.對任意的i，0≤i≤n，若

下面列舉來自于文獻［10］中對偶混合體積的一些基本性質，以備下文所用.

性質2.1［10］設K，Ki，Li∈Sn（1≤i≤n），則

仿照凸體的相對Steiner公式，我們引入星體的對偶相對steiner公式.

引理2.1 設K，E∈Sn，則對任意的實數λ≥0，有

我們稱（2.4）式為K相對于E的對偶Steiner公式，簡稱對偶Steiner公式.

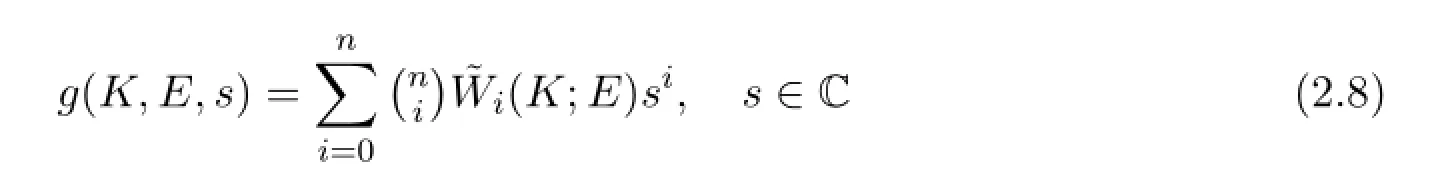
為星體K相對于星體E的對偶Steiner多項式，簡稱對偶Steiner多項式.

3 主要定理及其證明

這一節中我們討論對偶Steiner多項式的根的性質，首先需要下面的一個引理.

［1］Schneider R.Convex Bodies.The Brunn-Minkowski Theory［M］.Encyclopedia of Mathematics and its Applications 44.Cambridge：Cambridge University Press，1993.

［2］Steiner J.über parallel Fl?chen［J］.Ges.Werke，1882，2：245-308.

［3］Henk M，Hernández Cifre M A.Notes on the roots of Steiner polynomials［J］.Rev.Mat.Iberoamericana，2008，24（2）：631-644.

［4］Henk M，Hernández Cifre M A.On the location of roots of the Steiner polynomials［J］.Bull.Braz.Math. Soc.，2011，42（1）：153-170.

［5］Hernández Cifre M A，Saorín E.On the roots of the Steiner polynomial of a 3-dimensional convex body［J］. Adv.Geom.，2007，7：275-294.

［6］Jetter M.Bounds on the roots of the Steiner polynomial［J］.Adv.Geom.，2011，11：313-317.

［7］Sangwine-Yager J R.Bonnesen-Style inequalities for Minkowski relative geometry［J］.Transactions of the American Mathematical Society，1988，307（1）：373-382.

［8］Oda T.Convex Bodies and Algebraic Geometry.An Introduction to the Theory of Toric Varieties［M］. Berlin：Springer-Verlag，1988.

［9］Sangwine-Yager J R.Mixed Volumes，in：Handbook of Convex Geometry［M］.Amsterdam：North-Holland，1993.

［10］Lutwak E.Dual mixed volumes［J］.Pacific J.Math.，1975，58：531-538.

［11］Marden M.Geometry of Polynomials［M］.2nd ed.USA：American Mathematical Society，1966.

Notes on roots of the dual Steiner polynomial

Zhang Deyan1，2，Ma Tongyi3
（1.School of Mathematical Sciences，Huaibei Normal University，Huaibei235000；2.Department of Mathematics，Tongji University，Shanghai200092；3.College of Mathematics and statistics，Hexi University，Zhangye734000）

Motivated by the Steiner polynomial for convex bodies，the dual Steiner polynomial for star bodies is defined.Furthermore，roots of the dual Steiner polynomial are discussed by applying the dual Aleksandrov-Fenchel inequality，and some inequalities involving roots of the dual Steiner polynomial are obtained，where these inequalities are just dual forms of those of the Steiner polynomial.

The Steiner polynomial，the dual Steiner polynomial，the dual Aleksandrov-Fenchel inequality

O186.5

A

1008-5513（2016）02-0111-08

10.3969/j.issn.1008-5513.2016.02.001

2015-04-07.

國家自然科學基金（11161019，11561020）；安徽省高校自然科學研究重點項目（KJ2016A635）；甘肅省科技計劃項目（145RJZG227）.

張德燕（1980-），博士，講師，研究方向：微分幾何與凸幾何分析.

2010 MSC:52A20，52A39