梯級小水電群動態多目標優化調度

王萬良，張羽方，徐新黎，李 笠

(浙江工業大學 計算機科學與技術學院，浙江 杭州 310023)

?

梯級小水電群動態多目標優化調度

王萬良，張羽方，徐新黎，李 笠

(浙江工業大學 計算機科學與技術學院，浙江 杭州 310023)

針對農村梯級小水電群多目標優化調度問題，建立了考慮發電量、生態需水和灌溉需水的多目標調度模型，不同于以往的固定多目標制定，提出了基于來水量和需水量關系的動態多目標選擇機制，使得各調度時間段內的調度目標更加合理.同時，提出新的基于動態擁擠距離的最大最小適應度函數并引入改進的強度Pareto進化算法中的環境選擇與配對選擇思想，設計了一種新的多目標混合粒子群算法，最后應用于江西瀘水河流域梯級小水電群調度，調度結果驗證了該模型和算法的有效性和可行性.

小水電群；多目標優化調度；動態多目標；多目標粒子群算法

我國農村小水電資源豐富，并且具有極大的開發潛力，數量龐大的農村小水電對農村的電力事業做出了巨大的貢獻，而農村梯級小水電群的高效發電技術也越來越引起研究者的重視.梯級小水電群水庫優化調度需要綜合考慮整個梯級的發電效益以及生態需水與灌溉用水保證等需求，是一個復雜、高維、動態和非線性的多目標多約束問題.近年來一些較為成熟的智能算法被廣泛用于水電優化調度及類似的車間調度中，如遺傳算法、粒子群算法和蟻群算法等[1-4]，但這些方法通常將多目標問題轉化為單目標多約束的形式后采用單目標優化算法進行求解，存在諸如求解單一、優化結果不準確等諸多缺陷與局限性，亟需探尋新的適合梯級小水電群調度的多目標調度方法.隨著多目標優化算法研究的興起，多目標粒子群算法用于梯級優化調度已受到越來越多的關注，多目標粒子群算法比起傳統方法和適用于單目標的智能算法具有更好的實用效果，在處理水庫多目標優化調度問題上體現了一定的優越性.一些學者將多目標智能算法應用于水庫多目標調度并取得了一定的成果：贠汝安和董增川等將NSGA-Ⅱ(Nondominated sorting genetic algorithm-Ⅱ)算法應用于兩目標水庫調度中，研究了不同算法參數取值對調度結果的影響[5]；覃暉和周建中等針對水庫多目標防洪優化調度問題，以自適應柯西變異為基礎提出了多目標差分進化算法，為水庫多目標防洪調度決策提供了一種新的調度方案生成方法[6]；肖剛和解建倉進一步將NSGA-Ⅱ算法進行改進并應用于水庫多目標防洪調度問題，取得了更好的求解效率[7]；徐國賓和王健等將遺傳算法應用于求解三峽水庫非汛期多目標優化調度，獲得了綜合效益最優的調度方案[8].在小水電優化調度方面，王萬良等分別針對單個小水電站和串聯小水電站群建立了發電量最大優化目標模型，并采用遺傳算法進行求解[9]；文獻[10]在此基礎上進一步研究，分別引入粒子群算法和自適應粒子群算法求解模型，實驗結果表明自適應粒子群算法仿真求解更優；羅云霞等將生態徑流約束引入以控制水位和棄水最小作為優化調度目標的優化調度模型中，并采用文化算法求解[11].同時，國外學者也對水庫多目標調度問題進行了研究，Chang Jiang和Wenguang Ma提出了一種自適應多目標遺傳算法并應用于水庫多目標調度問題，更好的解決了求解中出現的早熟等問題[12]；Tiantian Yang，Xiaogang Gao，Scott Lee Sellars等設計了一種改進的多目標進化算法，并應用于美國加州的一處水電站取得很好的效果[13]；Huifeng Zhang，Jianzhong Zhou，Na Fang等將混沌神經網絡引入差分進化算法，并且將生態環境因素考慮到多目標調度問題里，為水庫多目標調度問題提供了新的求解思路[14].此外，量子多目標粒子群優化算法、多目標差分進化算法等較為先進的多目標優化算法被逐漸引入水庫多目標優化問題中[15-16]，然而多目標優化算法與水庫優化調度尤其是農村梯級小水電群優化調度的結合還亟待進一步的探索與改善.

目前多目標優化算法與梯級優化調度的結合還存在主要兩方面問題，一是調度目標固定化，即當前的多目標調度通常對調度期內所有時間段中的調度目標均預先設置為固定且相同的目標，缺乏靈活性，相反實際調度中由于每個時間段內來水量和需水量等因素的影響，導致調度目標并不相同，因此，需要新的調度目標確定方法；二是多目標優化算法在適應度函數設計、外部檔案維護和全局與局部最優解選擇等方面還有很大的改進空間，近年來，多目標優化算法逐漸成為智能算法研究熱點，許多新的改進算法被相繼提出[17-20].基于此，筆者建立了基于動態選擇的多目標調度模型，并進一步嘗試將改進的強度Pareto進化算法(SPEA2)[21]中的環境選擇與配對選擇思想引入基于最大最小化函數的多目標粒子群算法中，設計了一種新的多目標混合粒子群算法，同時將江西瀘水河流域梯級水庫作為調度實例，調度結果驗證了調度模型的合理性和算法的實用性.

1 引入動態多目標選擇的梯級小水電群多目標優化調度模型

1.1 目標函數

設某流域梯級小水電群中共有H個小水電站，由I個并聯電站和J個串聯電站組成.其中并聯形式的小水電站編號依次為A1，A2，…，AI；串聯形式的小水電站編號依次為B1，B2，…，BJ.梯級小水電群的拓撲結構圖如圖1所示.

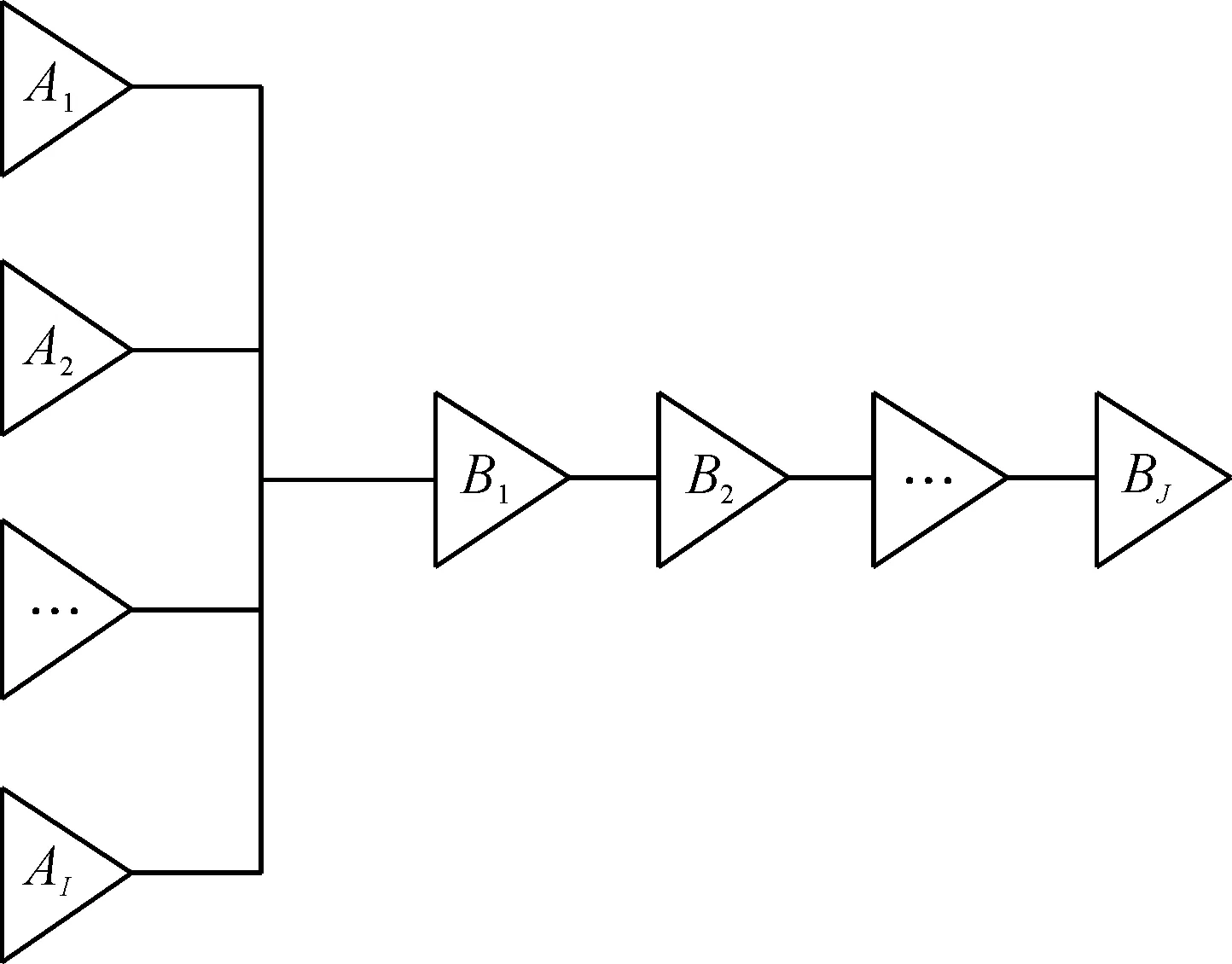
圖1 梯級小水電群拓撲結構Fig.1 Topology of cascade small hydropower stations

基于上述梯級小水電拓撲結構圖，建立了考慮發電、生態和灌溉三方面的多目標調度模型[22]，其中灌溉需水從庫區引水灌溉.增大發電量是為了保證電力公司利益最大化，而保證河道生態需水差和灌區的灌溉用水差最小是為了在保持整個流域的環境的前提下盡可能減少放水量，從而使水庫的水位長期處于較高的位置.

發電量最大目標為

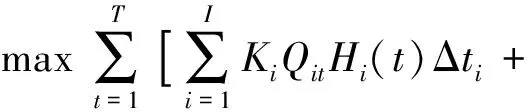
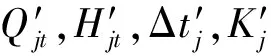
保證生態缺水量最小目標為

(2)

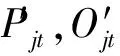
保證灌溉缺水量最小目標為

(3)

1.2 約束條件

約束條件包括以下幾項.

1) 水庫庫容約束為

(4)

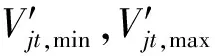
2) 出力約束為

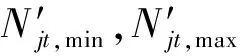
(6)

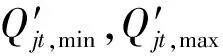
4) 串聯水庫水量平衡為

Vit=Vi,t-1+qit-(Qit+Sit+Git+Zit)

(7)

式中：Vit,Vi,t-1，分別為串聯水庫i在t時段和t-1時段的庫容；qit為串聯水庫i在t時段的區間來水量；Qit，Sit，Git，Zit分別為串聯水庫i在t時的發電流量、棄水、灌溉流量和蒸發量.

5) 并聯水庫水量平衡為

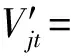
(8)

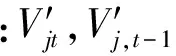
6) 串并聯流域交接處水庫水量平衡為

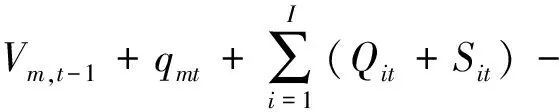
(9)

式中：Vm,t，Vit，Vm,t-1分別為串并聯流域交接處水庫m在t時段和t-1時段的庫容；qmt為串并聯流域交接處水庫m在t時段的區間來水量；Qit，Sit分別為串聯水庫i在t時的發電流量和棄水量；Qmt，Smt，Gmt，Zmt分別為串并聯流域交接處水庫m在t時的發電流量、棄水、灌溉流量和蒸發量.

7) 非負條件約束：上述的所有變量均為非負變量≥0.

1.3 動態多目標選擇

當前水庫多目標優化調度通常采取的是在調度期內的所有時間段中都以固定不變的多個目標來進行調度，然而通過實際調研發現在水庫的實際運行中，不同時間段受來水量與需水量之間差值不同的影響，導致實際的調度目標并不一致，在某些時間段中某個目標需要被考慮而在另外的時間段中并不需要將其考慮進調度目標中，故當前的調度方式較為死板，缺乏高效性與靈活性，調度結果與實際的多目標調度需求也存在一定差異.基于此，提出了一種動態多目標選擇方法，引入選擇因子，即

θi(t)=δi(t)-μi(t)

(10)

式中：θi(t)為電站i在t時段的選擇因子值；δi(t),μi(t)分別為電站i在t時段的來水量和電站下游河道的需水量.當θi(t)大于閾值αi時，來水量相對較為豐富，可供調配的水資源比較充沛，通常流域處于灌溉期，因此調度目標采用三個目標F，即發電量最大目標E，保證生態缺水量最小目標F，保證灌溉缺水量最小目標U；當0≤θi(t)≤αi時，考慮發電量最大目標F和保證生態缺水量最小目標E；而當θi(t)≤時，由于來水量相對匱乏，且流域通常不處于灌溉期，因此優先考慮下游生態用水保證，此時選擇保證生態缺水量最小目標E.動態多目標選擇機制為

(11)

式中：obji(t)為電站i在t時段的調度目標；閾值αi由調度人員憑經驗設置合適的值.經過實際調研，動態多目標選擇機制所確定的調度目標比較符合實際調度目標需求.

2 改進的多目標混合粒子群算法CDMOPSO

2.1 算法基本原理

針對上述多目標調度模型，如何能快速獲得分布均勻、靠近真實Pareto前沿的調度方案是多目標優化算法追求的目標，其中的關鍵技術包括適應度函數確定、外部檔案維護和全局最優解選取等.筆者提出的多目標混合粒子群算法CDMOPSO設計了改進的基于動態擁擠度的最大最小適應度函數，同時，算法對全局外部檔案更新策略進行改進，引入經典多目標算法SPEA2[21]中的環境選擇和配對選擇思想來進行外部檔案維護，在個體動態檔案維護中采用文獻[23]中的截斷式保留策略.

算法運行過程中，對于調度周期中不同調度時間段內調度目標個數不同的情況，在每次迭代時采用相同的當前種群狀態進行計算并疊加，以保證算法的連續性與準確性.

2.2 改進的基于動態擁擠距離的最大最小適應度函數

2003年，Balling首次將Maximin Fitness函數用于求解多目標優化問題[24]，并利用Maxmin Fitness函數來判斷非支配解.對一個最小化問題，若種群規模為N，目標函數的個數為M，則第i個個體Xi的Maximin Fitness函數為

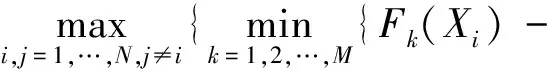
(12)

式(12)中，進行了兩輪比較：min函數首先在1到M個目標中運行；max函數再在所有1到N個候選解中(除去Xi)運行.通過觀察上式可以發現，所有Fmaximin小于0的決定向量都是非劣解，且適應度值越小該非劣解越優，因此最大最小適應度函數是一個求解多目標優化問題的有效工具.然而，單獨使用最大最小適應度函數值只能反映出不同粒子間的支配與非支配關系，缺乏保留種群多樣性的能力，基于此算法提出了改進的基于動態擁擠距離的最大最小適應度函數FMD，對于第i個個體Xi適應度函數為

FMD(Xi)=Fmaximin(Xi)Ddis(Xi)

(13)

式中Ddis(Xi)為個體i的擁擠距離[23]，即與其相鄰個體i+1與i-1間每個目標值差的絕對值之和，其計算式為

(14)

式中Fm(i)為個體i在子目標m上的函數值，擁擠距離的大小表示了解分布的分散程度，擁擠距離越大表明解分布越稀疏，如圖2所示.

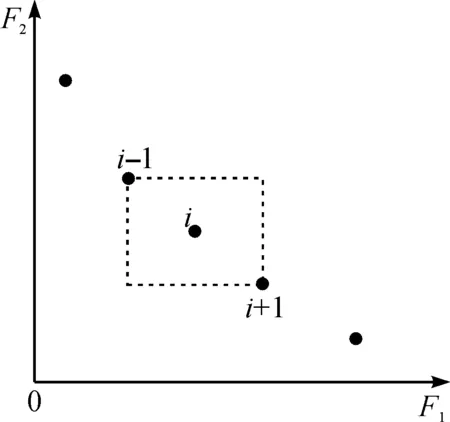
圖2 擁擠距離示意圖Fig.2 Schematic diagram of crowding distance

對于適應度函數FMD，由于非劣解的Fmaximin小于0且越小越好，而擁擠距離Ddis(Xi)為正數且越大越好，因此粒子的適應度函數FMD值越小則代表該粒子越優秀.

由于解分布的分散程度直接影響種群的多樣性，因此改進后的適應度函數FMD在保留了原有最大最小適應度函數能快速判斷粒子支配關系這個優點的同時，增加了對種群多樣性的考慮.

2.3 全局外部檔案集維護

在全局外部檔案維護方面，將進化算法SPEA2[18]中的環境選擇和配對選擇思想引入全局外部檔案維護中，為了避免過早收斂和停滯現象的發生，加入錦標賽選擇策略.全局外部檔案的定義如下：

全局外部檔案EA：用來存儲歷史全局最優非支配解的集合，長度為NG.

粒子速度位置更新公式為

vi(k+1)=ωvi(k)+c1r1[pBi-xi(k)]+ c2r2[gB-xi(k)]

(15)

xi(k+1)=vi(k+1)+xi(k)

(16)

式中：i為粒子索引；k為離散時間索引；vi(k)為第i個粒子在第k代的速度；xi(k)為第i個粒子在第k代的位置；ω為慣性權重；c1為認知加速常數；c2為社會加速常數；r1，r2為[0,1]區間內的隨機數；pBi為第i個粒子的個體最優位置(個體最優)；gB為粒子群群體歷史最優位置(局部最優).

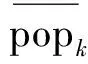
2.4 算法步驟

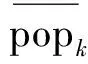
步驟2 根據式(10，11)確定每個調度時間段內的調度目標.

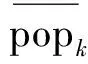
步驟7 從EA和pEA中選出當前種群的個體最優位置pBi和全局最優位置gB.

步驟8 設置k=k+1，判斷是否達到終止條件(k>G)，若滿足，則輸出非劣解集；否則轉步驟4.

2.5 算法復雜度分析

假設目標函數個數為M，粒子種群規模為P，迭代次數為K，全局外部檔案EA的大小NG(NG·P)，個體動態外部檔案pEA的大小NP(NP·P).算法每一代的時間復雜度主要由基于FMD適應度函數計算和EA及pEA的維護更新操作.

計算所有粒子FMD適應度函數值的時間復雜度為O(M·P2)，計算EA和pEA中的FMD適應度函數值的時間復雜度為O(M·NG2)+O(M·NP2)，EA和pEA中的粒子根據FMD適應度函數值排序的最壞時間復雜度為O(NGlog(NG))和O(NPlog(NP)).因此迭代K次的時間復雜度最壞為

K·{O(M·P2)+O(M·NG2)+O(M·NP2)+

O(NGlog(NG))O(NPlog(NP))}≈O(M·P2)

(17)

2.6 算法數值分析

為了驗證算法的有效性，對筆者算法的代距GD，間距S和最大覆蓋度MS進行測試[25]，限于篇幅限制，僅選用國際上具有代表性的多目標問題測試集ZDT系列[26]的ZDT3函數進行測試，并同三種多目標算法NSGA-Ⅱ，MOPSO[27]，DMOPSO[25]進行比較，參與比較的算法參數設置參考MOPSO[28]推薦的參數并采用相同的參數，具體如下：粒子規模為100，全局外部檔案和個體動態檔案大小為100，在模型運算當中迭代200 次，粒子飛行最大速度為可行范圍的1/8，慣性權重λ設為0.7，學習因子c1=c2=2，各算法獨立運行20 次，結果如表1所示.

表1 算法對比測試結果

Table 1 Algorithm contrast test results

結果NSGA?ⅡGDSMSMOPSOGDSMSDMOPSOGDSMSCDMOPSOGDSMS最佳0．00750．05100．8120．00360．03680．8420．00210．02730．8970．00180．02260．931最差0．00510．06720．7930．00530．04100．8120．00370．04100．8730．00340．03740．923平均0．00620．05860．8040．00420．03820．8300．00290．034100．8830．00250．03180．927

由表1可見：筆者所提的改進的多目標混合粒子群算法CDMOPSO與其他幾個算法相比，體現算法收斂性的指標代距GD值更小，因此擁有較好的收斂性，同時，間距S的值更小而最大覆蓋度MS的值更大，證明了筆者所提算法的解集擁有更優秀的多樣性.

3 實例計算

3.1 基本資料

以瀘水河流域梯級小水電群聯合調度為例.該

流域主要分布有九個水電站，包括社上電站、巖頭陂電站、海華一級電站、海華二級電站、安福渠電站、東谷電站、安平電站、洋田電站以及觀山電站.流域結構示意圖如圖3示，各電站特征參數如表2所示，其中社上、東谷電站和巖頭陂電站均為水庫型電站，具備一定的調節能力，其余電站均為徑流式或引水式電站，因此調節能力較差.其中社上電站和東谷電站需要承擔保護下游河道生態和保證下游灌溉區內灌溉用水的任務，因此在調度時需考慮生態需水和灌溉保證的多個目標.

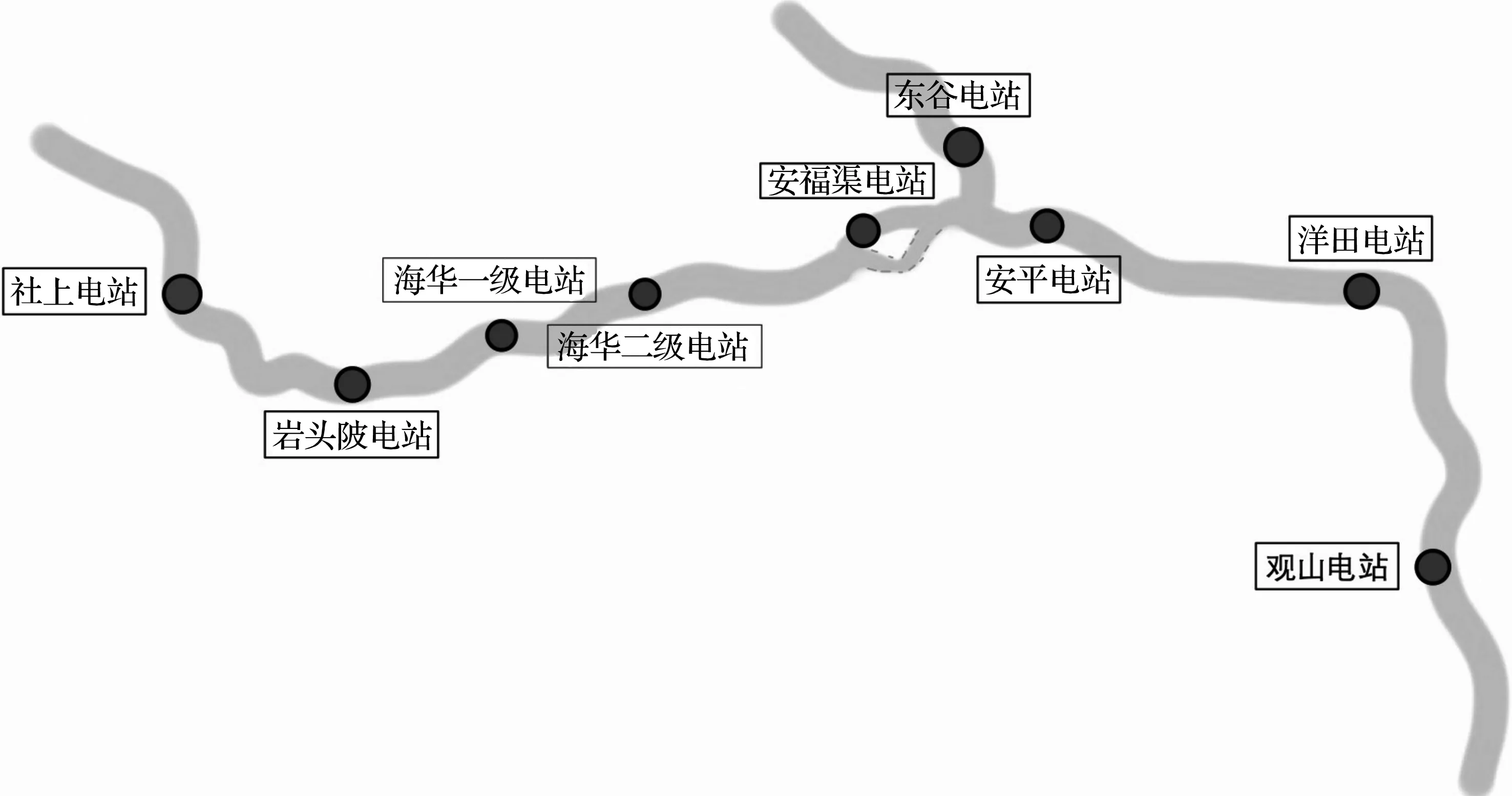
圖3 瀘水河梯級小水電群示意圖Fig.3 Diagram of Lushui river cascade small hydropower stations

Table 2 Basic information of cascade hydropower stations on river Lushui

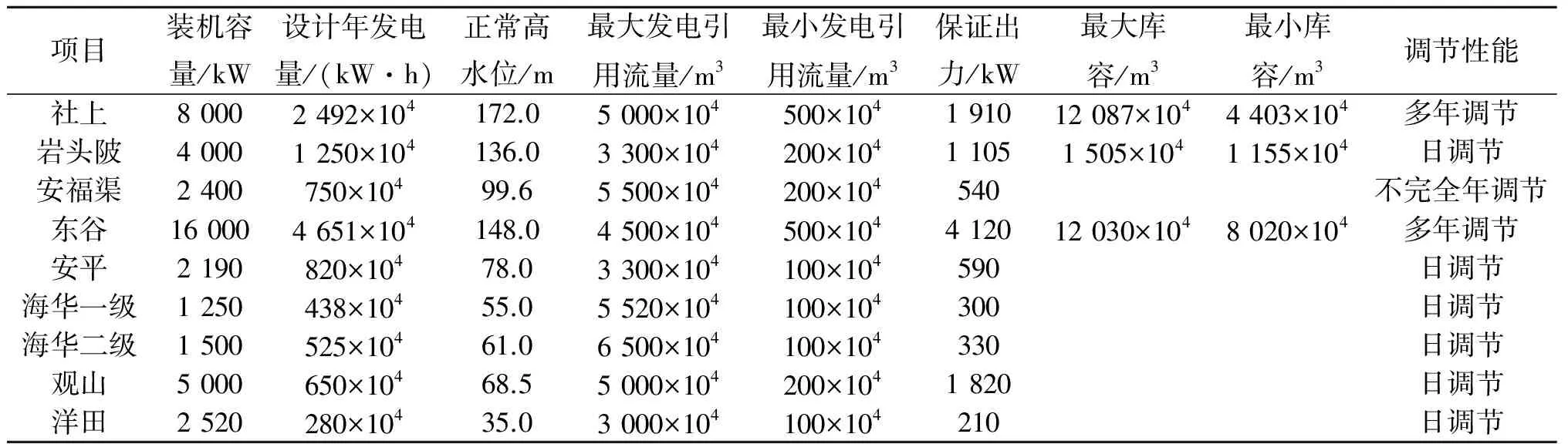
項目裝機容量/kW設計年發電量/(kW·h)正常高水位/m最大發電引用流量/m3最小發電引用流量/m3保證出力/kW最大庫容/m3最小庫容/m3調節性能社上80002492×104172．05000×104500×104191012087×1044403×104多年調節巖頭陂40001250×104136．03300×104200×10411051505×1041155×104日調節安福渠2400750×10499．65500×104200×104540不完全年調節東谷160004651×104148．04500×104500×104412012030×1048020×104多年調節安平2190820×10478．03300×104100×104590日調節海華一級1250438×10455．05520×104100×104300日調節海華二級1500525×10461．06500×104100×104330日調節觀山5000650×10468．55000×104200×1041820日調節洋田2520280×10435．03000×104100×104210日調節

3.2 約束處理策略

約束處理是模型求解的關鍵問題，梯級電站優化調度中最常用的約束處理方法是懲罰函數[28]，然而瀘水河流域梯級小水電群電站較多且約束條件較為復雜，若使用懲罰函數處理將會大大增加問題求解的時間復雜度，因此根據瀘水河流域實際情況，并參考文獻[29]中的方法對約束條件進行轉化處理.瀘水河流域梯級小水電群的優化調度主要包括水位(庫容)、發電流量和出力約束，水位約束處理較為簡單，若調度中該時段水庫水位超過水位約束區間，則將其限定于可行域之內即可，對于發電流量約束，將發電流量約束根據水量平衡方程轉換為水位約束，再根據逐時段推求水位可行域方法將出力約束轉化為各時段水位約束，最后，將上述所得的3個水位約束取交集，即可得到每個調度時段內水位決策變量的約束條件.經過以上約束條件處理后，每個調度時段內的限制條件便只有水位一項，從而降低了問題求解的時間復雜度.

3.3 調度結果

采取月調度原則，以年為周期，月為調度單位時

間，河道推薦適宜生態徑流量和推薦適宜灌溉需水量的值采用逐月頻率計算法[30]確定.借鑒經典多目標粒子群算法MOPSO[28]的參數設置并經過多次試算調整后，算法參數設置如下：粒子規模為100，全局外部檔案和個體動態檔案大小為100，在模型運算當中迭代200 次，粒子飛行最大速度為可行范圍的1/8，慣性權重設為0.7，學習因子c1=c2=2，保存10 個非劣解作為結果.

首先確定調度目標.來水量、生態需水量和灌溉需水量采用瀘水河流域75%來水頻率典型年數據，圖4(a，b)分別為社上電站和東谷電站的來水量及需水量變化曲線圖.根據調度經驗，社上電站和東谷電站的動態多目標選擇閾值αi分別設置為2 000，2 700 萬m3，由動態多目標選擇式(10，11)計算可得1～4 月及8～12 月社上電站和東谷電站的調度目標為發電量最大化和保證生態缺水量最小兩個目標，5～7 月間社上電站和東谷電站的調度目標為發電量最大化、保證生態缺水量最小和保證灌溉缺水量最小三個目標.接下來采用3節所提出的混合多目標粒子群算法對瀘水河流域梯級小水電群進行多目標優化調度.

圖4 社上電站和東谷電站每月來水與需水曲線圖Fig.4 Curve of inflow and water needs in each month of Sheshang station and Donggu station

調度結果如表3所示，可以看出：電站總發電量與下游河道缺水量形成明顯的反比關系，兩者相互競爭、相互制約，如果提高年發電量，則河道的缺水量會隨之提高，反之，若要盡量滿足河道的需水量則會犧牲一定的發電量.不同于利用單目標優化算法進行求解獲得的單一解，多目標優化調度可以獲得更多的候選調度解并且將多個目標考慮在內，為電站管理人員制定調度方案提供更多合理科學的選擇.

進一步，選擇方案6，8這兩個代表方案和常規調度進行水位對比分析，圖5所示為各調度方案在調度期內的社上水庫和東谷水庫的水位過程曲線對比.如圖5(a)所示，1～4 月及8～12 月中，多目標調度方案6和8在保證社上電站發電量和下游河道生態需水量的基礎上將水位保持在盡量高的位置，相較于常規方案水位提高了1%～4.6%，在5～7 月豐水期中，來水量較大，多目標調度方案6，8不僅同時滿足發電量、生態需水和灌溉需水三個目標，同時將水位維持在170 m的較高位置，達到了良好的調度效果，調度方案6和8的全年最高最低水位差分別為5.8，6.8 m，相較于常規調度的10.85 m分別減少了46.5%和37.3%，使社上水庫全年的水位維持在較高的位置.

表3 瀘水河梯級小水電站群多目標優化調度結果表

Table 3 Multi-objective optimization scheduling results of Lushui river cascade hydropower stations

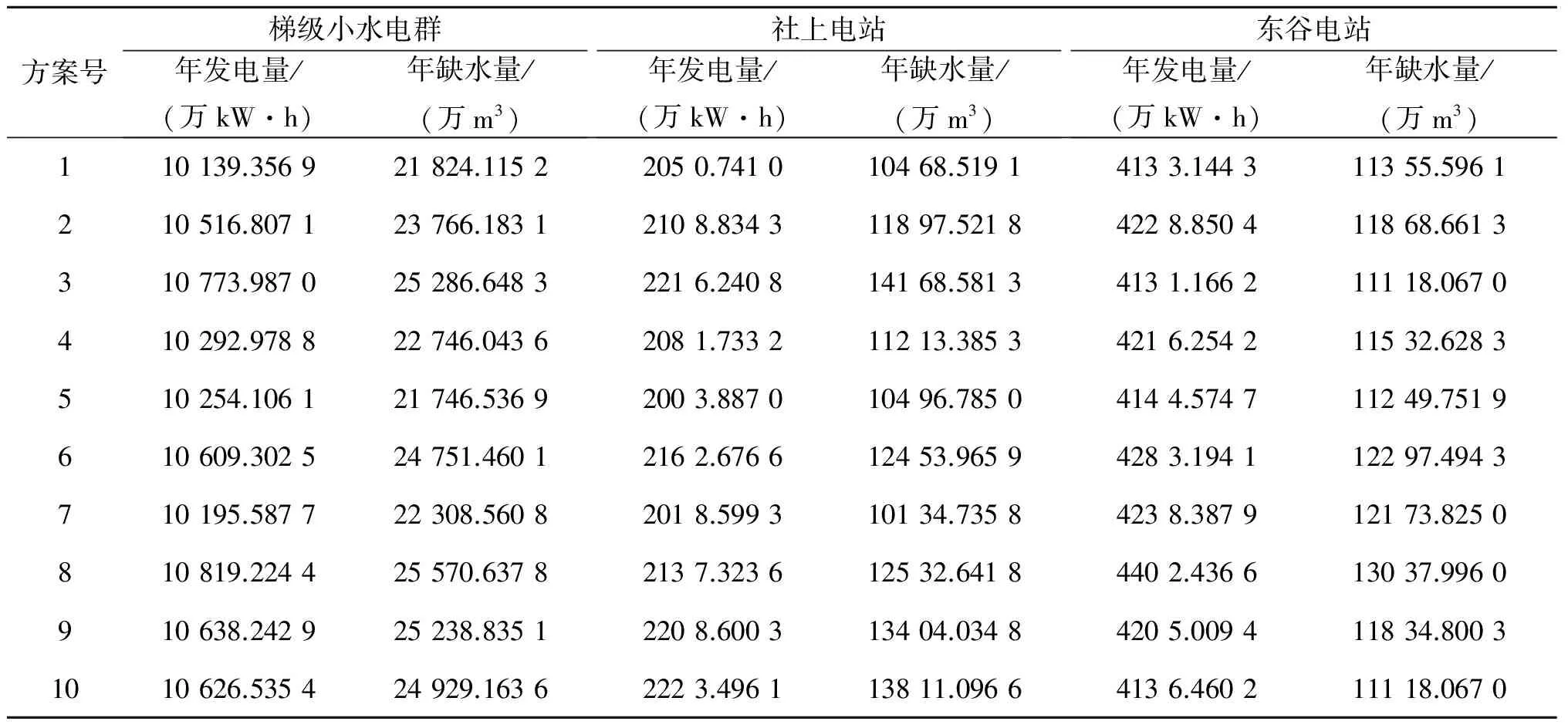
方案號梯級小水電群年發電量/(萬kW·h)年缺水量/(萬m3)社上電站年發電量/(萬kW·h)年缺水量/(萬m3)東谷電站年發電量/(萬kW·h)年缺水量/(萬m3)110139．356921824．11522050．741010468．51914133．144311355．5961210516．807123766．18312108．834311897．52184228．850411868．6613310773．987025286．64832216．240814168．58134131．166211118．0670410292．978822746．04362081．733211213．38534216．254211532．6283510254．106121746．53692003．887010496．78504144．574711249．7519610609．302524751．46012162．676612453．96594283．194112297．4943710195．587722308．56082018．599310134．73584238．387912173．8250810819．224425570．63782137．323612532．64184402．436613037．9960910638．242925238．83512208．600313404．03484205．009411834．80031010626．535424929．16362223．496113811．09664136．460211118．0670

圖5(b)所示為東谷水庫的水位過程曲線對比，在1～4 月及8～12 月中，多目標調度方案6和8相較于常規調度方案水位提高了3.1%～13.1%，提升較為明顯，在5～7 月的豐水期中，東谷電站在滿足發電量、生態需水和灌溉需水三個目標的同時，水位保持在149 m的較高水位，相較于常規調度提高了3%～5.7%，調度方案6，8的全年最高最低水位差均為8 m，相較于常規調度的15.01 m減少了46.7%，使東谷水庫全年的水位維持在較高的位置.由以上對比可以看出：筆者所提出的調度方法相較于常規調度，不僅滿足發電量和河道需水的目標，同時將水庫的水位維持在較高的穩定范圍內，達到了較好的調度效果.

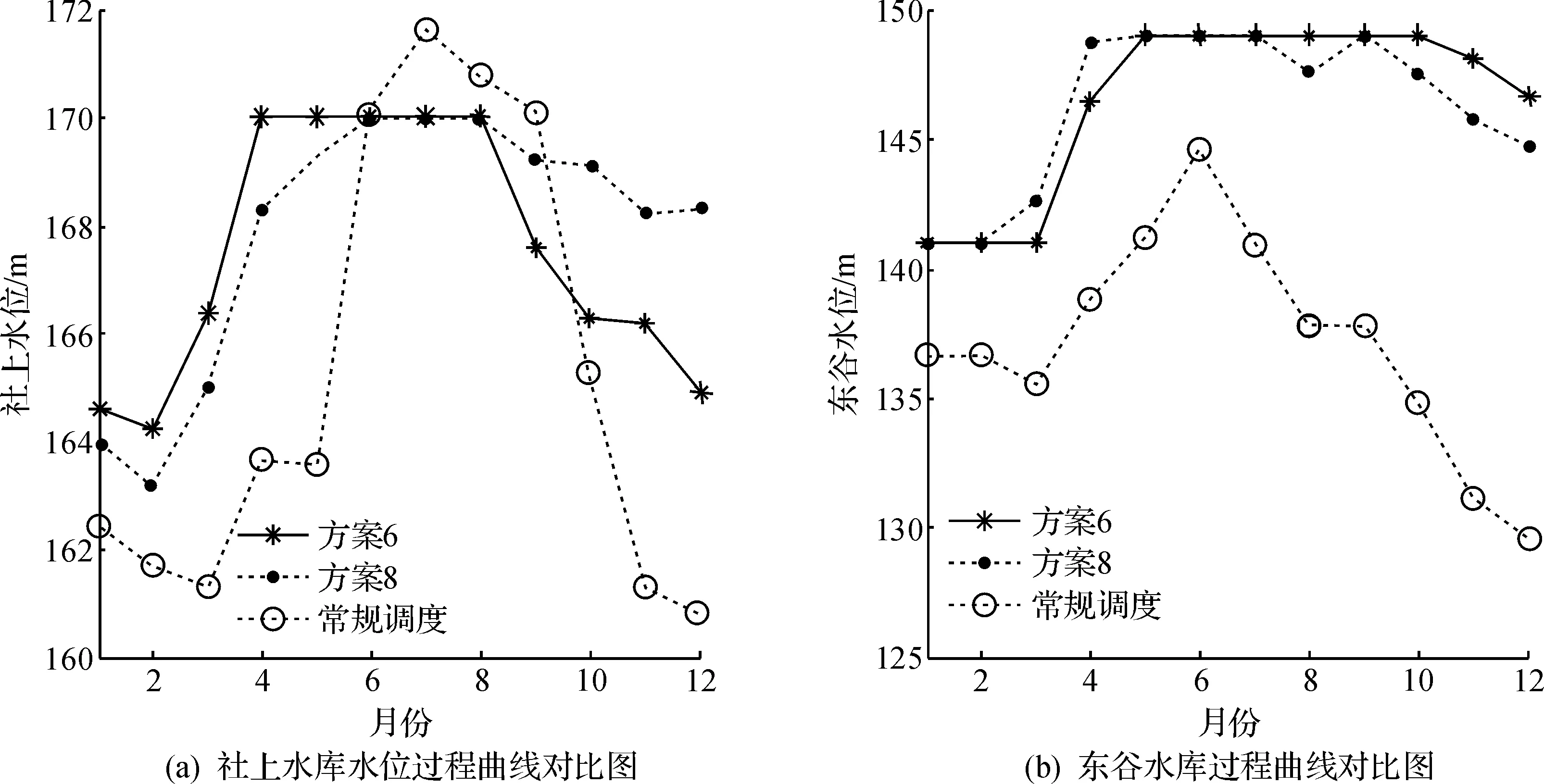
圖5 社上水庫和東谷水庫典型方案水位過程曲線對比Fig.5 Level of Sheshang reservior and Donggu reservoir in typical schemes

為了驗證1.3節所提的動態多目標選擇方法對調度結果的影響，將使用了動態多目標選擇方法進行調度的方案6，8與使用全年固定三個目標進行調度的固定多目標調度方案進行對比，社上電站和東谷電站的下泄流量過程曲線對比如圖6所示，在1～5 月和9～12 月時間段中，實際調度并不需要考慮灌溉需水這一目標，然而固定多目標調度依然將其考慮在內，導致固定多目標調度方案在此調度時間段內下泄流量增大，造成了不必要的浪費，從而犧牲了部分發電效益，表4顯示了方案6，8和固定多目標調度方案的年發電量對比，可以看出方案6，8相較于固定多目標方案，年發電量分別提升了3.22%和5.26%，故方案6，8的下泄流量則更為合理，因此，所提的動態多目標選擇方法可以有效地根據來水量與需水量動態確定不同調度時間段內的調度目標，使得調度結果更為高效合理.

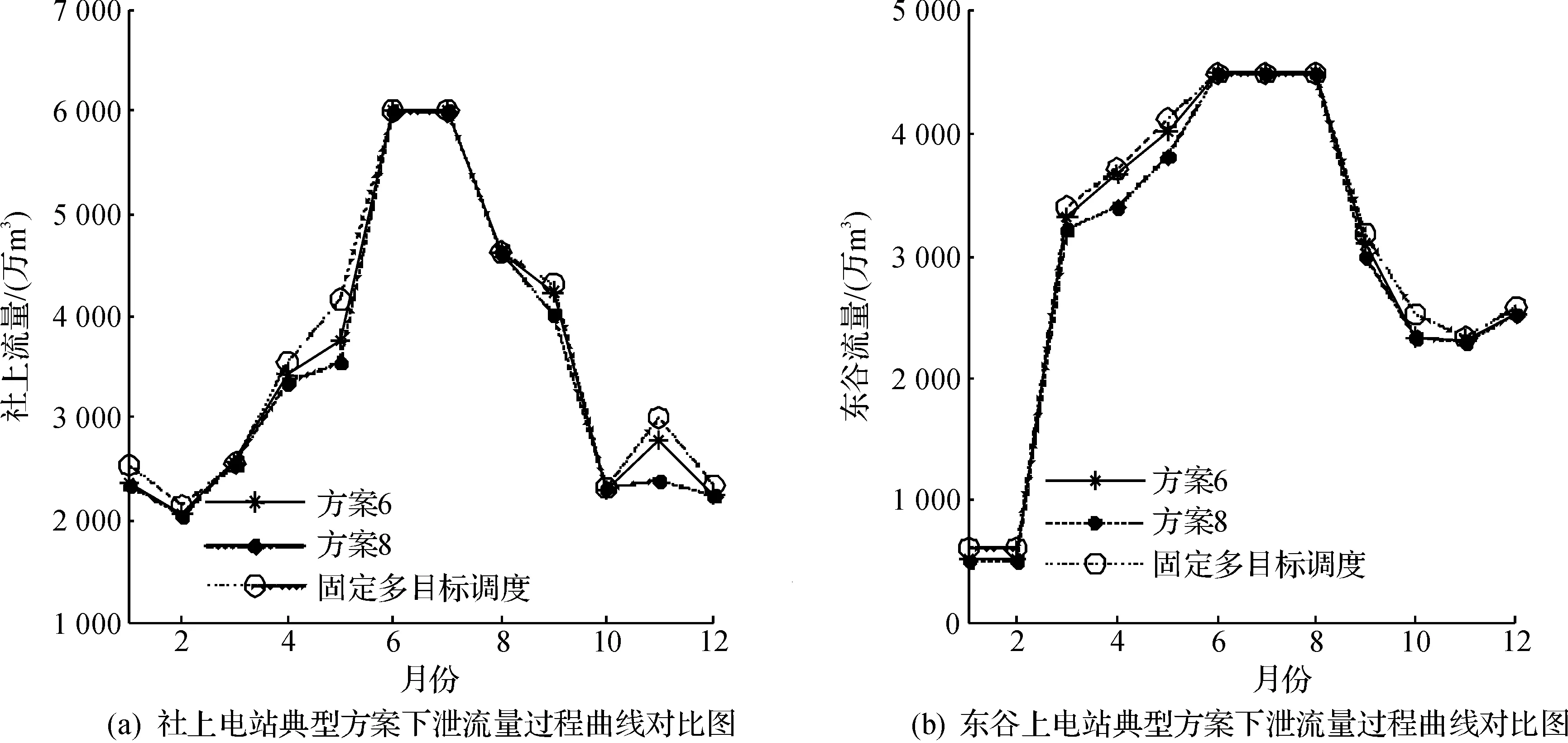
圖6 社上電站和東谷電站典型方案下泄流量過程曲線對比圖Fig.6 Discharged flow of Sheshang station and Donggu station in typical schemes

表4 瀘水河梯級小水電站群典型調度方案年發電量對比

Table 4 Annual electricity production of Lushui river cascade hydropower stations in typical schemes 萬kW·h

4 結 論

針對農村梯級小水電群多目標優化調度問題，首先建立了考慮發電量、生態需水和灌溉需水的多目標調度模型，不同于以往的固定多目標制定，提出了基于來水量和需水量關系的動態多目標選擇機制，使得各調度時間段內的調度目標更加合理.在此基礎上，對多目標粒子群算法進行改進，提出基于動態擁擠距離的最大最小適應度函數，并引入經典多目標算法SPEA2中的環境選擇和配對選擇思想，設計了新的混合多目標粒子群算法.最后將上述模型和算法應用于江西瀘水河流域梯級小水電群中，調度結果表明：所提出的模型和算法不僅合理的滿足了發電量、河道生態需水和河道灌溉需水的目標，并且使水庫水位在調度期內保持在較高位置，獲得了良好的調度效果，為今后電站管理人員制定調度方案提供了新的思路和方法.

[1] 鄭姣,楊侃,倪福全,等.水庫群發電優化調度遺傳算法整體改進策略研究[J].水利學報,2013,44(2):205-211.

[2] 徐新黎,楊丹,王萬良,等.混聯水庫群分時電價下優化調度模型研究[J].浙江工業大學學報,2015，43(4):431-437.

[3] 陳勇,盛家君,王亞良,等.基于改進蛙跳算法的可重構裝配線調度研究[J].浙江工業大學學報,2014，42(3):274-279.

[4] 董輝,黃勝.二維排樣中小生境粒子群算法的研究與應用[J].浙江工業大學學報,2014，42(3):257-259.

[5] 覃暉,周建中,王光謙,等.基于多目標差分進化算法的水庫多目標防洪調度研究[J].水利學報,2009,40(5):513-519.

[6] 贠汝安,董增川,王好芳.基于NSGA2的水庫多目標優化[J].山東大學學報(工學版),2010,40(6):124-128.

[7] 肖剛,解建倉,羅軍剛.基于改進NSGAII的水庫多目標防洪調度算法研究[J].水力發電學報,2012,31(5):77-83.

[8] 徐國賓,王健,馬超.耦合水質目標的三峽水庫非汛期多目標優化調度模型[J].水力發電學報,2011,30(3):78-84.

[9] 王萬良,周慕遜,管秋,等.基于遺傳算法的小水電站優化調度方法的研究與實踐[J].水利發電學報,2005,24(3):6-11.

[10] 羅云霞,王萬良,周慕遜.基于自適應粒子群算法的梯級小水電群優化調度研究[J].水力發電學報,2008,27(4):7-10+6.

[11] 羅云霞,王萬良,周慕遜.小水電優化調度數學模型及其基于文化算法的比較研究[J].水力發電學報,2009,28(4):187-192.

[12] CHANG Jiang, MA Guangwen. Research on multi-objective reservoir optimal operation based on adaptive genetic algorithms[J]. Advanced materials research,2014,926:2042-2045.

[13] YANG Tiantian, GAO Xiaogang, SELLARS S L, et al. Improving the multi-objective evolutionary optimization algorithm for hydropower reservoir operations in the California Oroville-Thermalito complex[J]. Environmental modelling & software,2015,69:262-279.

[14] ZHANG Huifeng, ZHOU Jianzhong, FANG Na, et al. An efficient multi-objective adaptive differential evolution with chaotic neuron network and its application on long-term hydropower operation with considering ecological environment problem[J]. International journal of electrical power & energy systems,2013,45(1):60-70.

[15] 羅軍剛,張曉,解建倉.基于量子多目標粒子群優化算法的水庫防洪調度[J].水力發電學報,2013,32(6):69-75.

[16] 王學敏,周建中,歐陽碩,等.三峽梯級生態友好型多目標發電優化調度模型及其求解算法[J].水利學報,2013,44(2):154-163.

[17] LI Ke, FIALHO A, KWONG S, et al. Adaptive operator selection with bandits for a multiobjective evolutionary algorithm based on decomposition[J]. Evolutionary computation, IEEE transactions on,2014,18(1):114-130.

[18] CHEN Bili, ZENG Wenhua, LIN Yangbin, et al. A new local search-based multiobjective optimization algorithm[J].

Evolutionary computation, IEEE transactions on,2015,19(1):50-73.

[19] HU Wang, YEN G G. Adaptive multiobjective particle swarm optimization based on parallel cell coordinate system[J]. Evolutionary computation, IEEE transactions on,2015,19(1):1-18.

[20] ZHANG Xingyi, TIAN Ye, CHENG Ran, et al. An efficient approach to nondominated sorting for evolutionary multiobjective optimization[J]. Evolutionary computation, IEEE transactions on,2015,19(2):201-213.

[21] ZITZLER E, LAUMANNS M, THIELE, et al. SPEA2: improving the strength pareto evolutionary algorithm[C]//HSU H. Proceedings of Eurogen: Evolutionary Methods for Design Optimization & Control with Applications to Industrial Problems. Athens: Citeseer,2001:8-13.

[22] 李文莉,李郁俠,任平安.基于云變異人工蜂群算法的梯級水庫群優化調度[J].水力發電學報,2014,33(1):37-42.

[23] 賈樹晉.熱軋生產計劃與負荷分配的多目標群智能算法研究[D].上海:上海交通大學,2012.

[24] BALLING R. The maximin fitness function; multi-objective city and regional planning[C]//CARLOS M. Evolutionary Multi-Criterion Optimization. Faro: Springer Berlin Heidelberg,2003:1-15.

[25] 李笠.考慮生態因素的小水電優化調度算法研究[D].杭州：浙江工業大學,2014.

[26] 鄭金華.多目標進化算法及其應用[M].北京:科學出版社,2007.

[27] COELLO C A C, PULIDO G T, LECHUGA M S. Handling multiple objectives with particle swarm optimization[J]. IEEE transactions on evolutionary computation,2004,8(3):256-279.

[28] 周建中,李英海,肖舸,等.基于混合粒子群算法的梯級水電站多目標優化調度[J].水利學報,2010,41(10):1212-1219.

[29] 盧有麟,周建中,王浩,等.三峽梯級樞紐多目標生態優化調度模型及其求解方法[J].水科學進展,2011,22(6):780-788.

[30] 李捷,夏自強,馬廣慧,等.河流生態徑流計算的逐月頻率計算法[J].生態學報,2007(7):2916-2921.

(責任編輯：陳石平)

Dynamic multi-objective optimal scheduling method for cascade small hydropower group

WANG Wanliang, ZHANG Yufang, XU Xinli, LI Li

(College of Computer Science and Technology, Zhejiang University of Technology, Hangzhou 310023, China)

For the optimization scheduling problem of rural cascade small hydropower group, a multi-objective scheduling model was built, which involved of energy output of hydropower station, ecological water requirement and irrigation water requirement. Different from previous fixed goal setting, dynamic multi-objective selection mechanism based on the relationship between runoff and water demand was proposed, where the scheduling objectives were appropriately determined at different scheduling period by the selective factor. Then, the maximin function based on dynamic crowding distance was proposed and the environment selection and pairing selection in improving the strength Pareto evolutionary algorithm were introduced, and a new hybrid multi-objective particle swarm optimization algorithm was designed. Finally, the proposed model and algorithm were applied to solve the multi-objective scheduling of cascade hydropower stations of Lushui River in JiangXi province. The scheduling results illustrate that the the model and algorithm are effective and feasible.

small hydropower stations; multi-objective optimal scheduling; dynamic selection; multi-objective particle swarm optimization

2016-03-08

“十二五”國家科技支撐計劃：農村小水電高效發電技術(2012BAD10B01)；國家自然科學基金資助項目(61379123，61203371)

王萬良(1957—)，男，江蘇高郵人，教授，博士，研究方向為人工智能、優化調度，E-mail：wwl@zjut.edu.cn.

TV697

A

1006-4303(2016)06-0591-10