基于噪聲輔助局部波動特征分解的齒輪裂紋故障定量診斷方法
吳家騰 彭曉燕 楊 宇 張 亢 程軍圣
1. 湖南大學(xué)汽車車身先進設(shè)計制造國家重點實驗室,長沙,4100822.長沙理工大學(xué),長沙,410076
?
基于噪聲輔助局部波動特征分解的齒輪裂紋故障定量診斷方法
吳家騰1彭曉燕1楊 宇1張 亢2程軍圣1
1. 湖南大學(xué)汽車車身先進設(shè)計制造國家重點實驗室,長沙,4100822.長沙理工大學(xué),長沙,410076
將齒輪故障機理研究與故障診斷方法相結(jié)合,提出了一種新的基于噪聲輔助局部波動特征分解的齒輪裂紋定量診斷方法。首先,建立了帶裂紋齒輪系統(tǒng)動力學(xué)模型,獲得不同裂紋程度下的動力學(xué)響應(yīng),從中提取對故障敏感而與工況無關(guān)的特征參數(shù)構(gòu)成特征向量矩陣,輸入到支持向量回歸機中,建立了特征參數(shù)與齒輪裂紋程度之間的映射關(guān)系。然后,通過這種映射關(guān)系,對實際的齒輪裂紋信號采用噪聲輔助LOD方法進行特征提取,實現(xiàn)了齒輪裂紋的定量診斷。
噪聲輔助;局部波動特征分解;特征提取;映射關(guān)系;齒輪裂紋定量診斷
0 引言
目前,國內(nèi)外針對齒輪系統(tǒng)的故障研究主要分為兩大類。一類是通過建立齒輪系統(tǒng)的動力學(xué)模型來反映齒輪故障機理行為的變化過程[1]。齒輪損壞的原因及故障嚴(yán)重程度通常與動力學(xué)參數(shù)相關(guān),即沿齒裂紋長度寬度和裂紋深度,均會不同程度地導(dǎo)致齒輪副的嚙合剛度變小[2-4]:如文獻[5]通過建立六自由度的齒輪裂紋故障的動力學(xué)模型來分析三種不同裂紋擴展?fàn)顩r的齒輪早期故障現(xiàn)象;文獻[6]運用有限元分析方法和赫茲接觸理論分析方法描述了齒輪嚙合傳動過程中齒輪嚙合剛度的變化過程。然而現(xiàn)階段的故障機理研究只是通過數(shù)值分析方法模擬出振動響應(yīng)并進行簡單的故障程度分析,并不能完全反映出齒輪故障產(chǎn)生的動力學(xué)機理過程。還有一類是基于信號處理方法對齒輪故障進行診斷。通常齒輪產(chǎn)生故障時,其振動信號大多表現(xiàn)出調(diào)制特征,要從此類信號中提取出表征齒輪故障現(xiàn)象的特征參數(shù)就需要引入信號處理方法:如經(jīng)驗?zāi)B(tài)分解(empirical mode decomposition,EMD)[7]方法、局部均值分解(local mean decomposition,LMD)[8]方法常被應(yīng)用于齒輪故障診斷。由于算法本身存在一些缺陷,使得兩種方法本身仍然存在問題[9-10]。局部波動特征分解(local oscillatory-characteristic decomposition,LOD)[11]是一種新提出的時頻分析方法,本質(zhì)上是根據(jù)信號的局部波動特征來實現(xiàn)信號的自適應(yīng)分解,得到一系列瞬時頻率具有物理意義的單一波動分量(mono-oscillatory component,MOC)。相比于EMD方法,LOD方法分解速度更快速高效,在抑制端點效應(yīng)上更有優(yōu)勢,已被應(yīng)用于齒輪故障的定性診斷,取得了較好的效果[12]。LOD方法同EMD與LMD一樣,在實際應(yīng)用過程中同樣受到信號間歇性等的影響,容易產(chǎn)生模態(tài)混淆現(xiàn)象,即同一個MOC分量包含著不同的波動模式,或同一種波動模式被分解到了不同的MOC分量中,從而使信號失去真實的物理意義。
針對以上存在的問題,本文將上述兩類方法進行結(jié)合,即將齒輪系統(tǒng)故障機理研究與故障診斷方法相結(jié)合,提出了基于噪聲輔助LOD的齒輪裂紋定量診斷方法。文章通過利用噪聲輔助LOD方法對實際的齒輪裂紋信號進行定量診斷,來實現(xiàn)故障機理研究和故障診斷的有機結(jié)合。
1 基于噪聲輔助的LOD方法
1.1 LOD模態(tài)混淆現(xiàn)象
LOD方法的主要思想是根據(jù)源信號自身的局部波動特征來對信號進行自適應(yīng)分解,其中LOD方法包含了微分運算、分段線性變換、坐標(biāo)域變換三種基本運算[11]。然而在實際中由于受到LOD算法本身的分解能力,以及采樣頻率、間歇性信號等的影響,很可能會發(fā)生模態(tài)混淆現(xiàn)象,即同一個MOC分量包含著不同的波動模式,或同一種波動模式被分解到了不同的MOC分量當(dāng)中,失去信號真實的物理意義。下面考察一個幅值為1、頻率為5 Hz的正弦信號和一個幅值為0.05、頻率為250 Hz的高頻間歇信號所組成的混合信號,如圖1所示。求解混合信號的均值曲線如圖2所示,由于混合了一個間歇信號以后,曲線在混淆部分變得紊亂,導(dǎo)致LOD分解后的第1個MOC分量ZMOC1(t)出現(xiàn)了模態(tài)混淆現(xiàn)象。從圖3可以看出,模態(tài)混淆現(xiàn)象使分量ZMOC1(t)中包含了低頻的正弦信號和高頻的間歇信號兩種不同尺度的波動形式,也就導(dǎo)致分量ZMOC1(t)失去了包含單一波動分量的物理意義,使得LOD方法失去了分析信號的價值。因此,提出一種基于噪聲輔助的改進方法來解決LOD模態(tài)混淆問題。
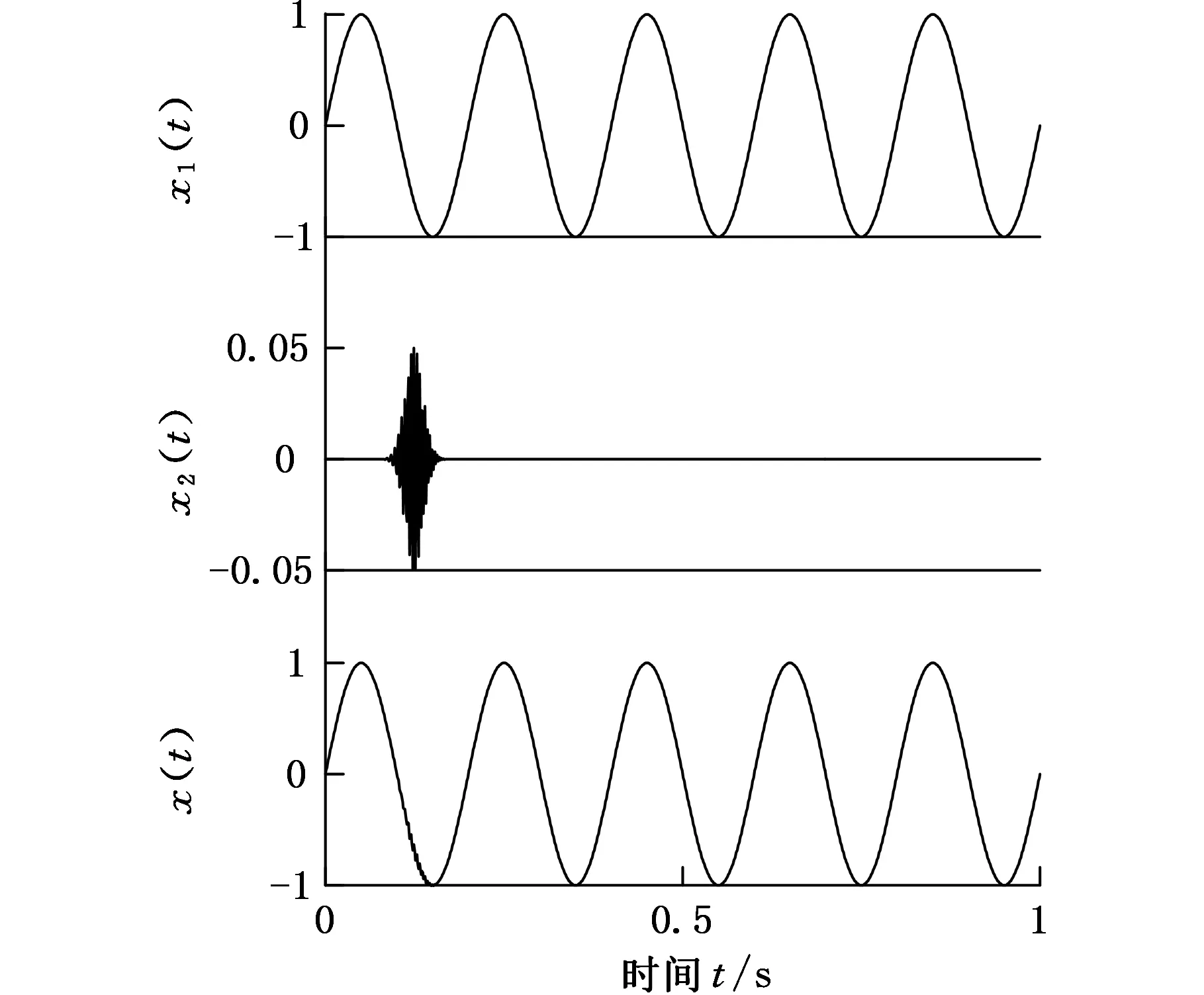
圖1 仿真信號曲線

圖2 仿真信號均值曲線

圖3 仿真信號LOD分解分量ZMOC1(t)
1.2 基于噪聲輔助的LOD方法
根據(jù)文獻[13]描述的白噪聲在整個頻率空間中均勻分布的統(tǒng)計特性,通過對目標(biāo)信號添加白噪聲再進行信號分解,白噪聲可以使目標(biāo)信號中的各個時間尺度均勻地分布在所確定的濾波器組的通頻帶之中,即顯著減小高頻間歇信號對LOD方法的干擾,從而可以使高頻間歇信號被徹底分解出來。本文擬將白噪聲引入LOD方法中進行輔助分析,其具體分解步驟如下:
(1)找到信號x(t)的所有極值Xk(k=1,2,…,M)及其對應(yīng)的時刻值τk,在任意兩個相鄰極值點[Xk,Xk+1)之間對x(t)進行線性變換,得到分段線性函數(shù)s1(t),為了減小分解誤差,采用坐標(biāo)域變換將(t,x)轉(zhuǎn)換成鋸齒域坐標(biāo)(u,s)。

(4)將原始信號的鋸齒域函數(shù)s1(u)減去鋸齒域均值函數(shù)m1(u),得到c1(u),c1(u)為一高頻波動函數(shù),利用反變換將c1(u)的坐標(biāo)從鋸齒域還原到原數(shù)據(jù)域c1(t)。
(5)如果c1(t)為一個瞬時頻率具有物理意義的單分量信號,則c1(t)為x(t)的第1個MOC分量ZMOC1(t),若不是,則將c1(t)作為原始信號重復(fù)步驟(1)~(4),循環(huán)m次,直至得到滿足分解條件的單分量信號cm(t),cm(t)即為信號x(t)的第一個分量ZMOC1(t)。
(6)重復(fù)步驟(1)~(5)多次,每次添加不同的白噪聲信號。
(7)對得到的多個ZMOC1(t)分量取平均值,均值化后的ZMOC1(t)作為分解結(jié)果。
再次考察圖1所示的仿真信號x(t),分別添加30次幅值為0.001的白噪聲并對仿真信號進行分解,將30次分解結(jié)果求平均值并作為分解的最終結(jié)果,如圖4所示。從圖4可以看出,高頻間歇信號被很好地分離出來;這里考慮到微分運算使得數(shù)值計算中白噪聲的零均值誤差問題被放大,如果直接對目標(biāo)信號添加白噪聲再進行整體LOD分解將會導(dǎo)致分量ZMOC2(t)受到白噪聲的污染,如圖5所示。EEMD方法分解仿真信號結(jié)果如圖6所示。
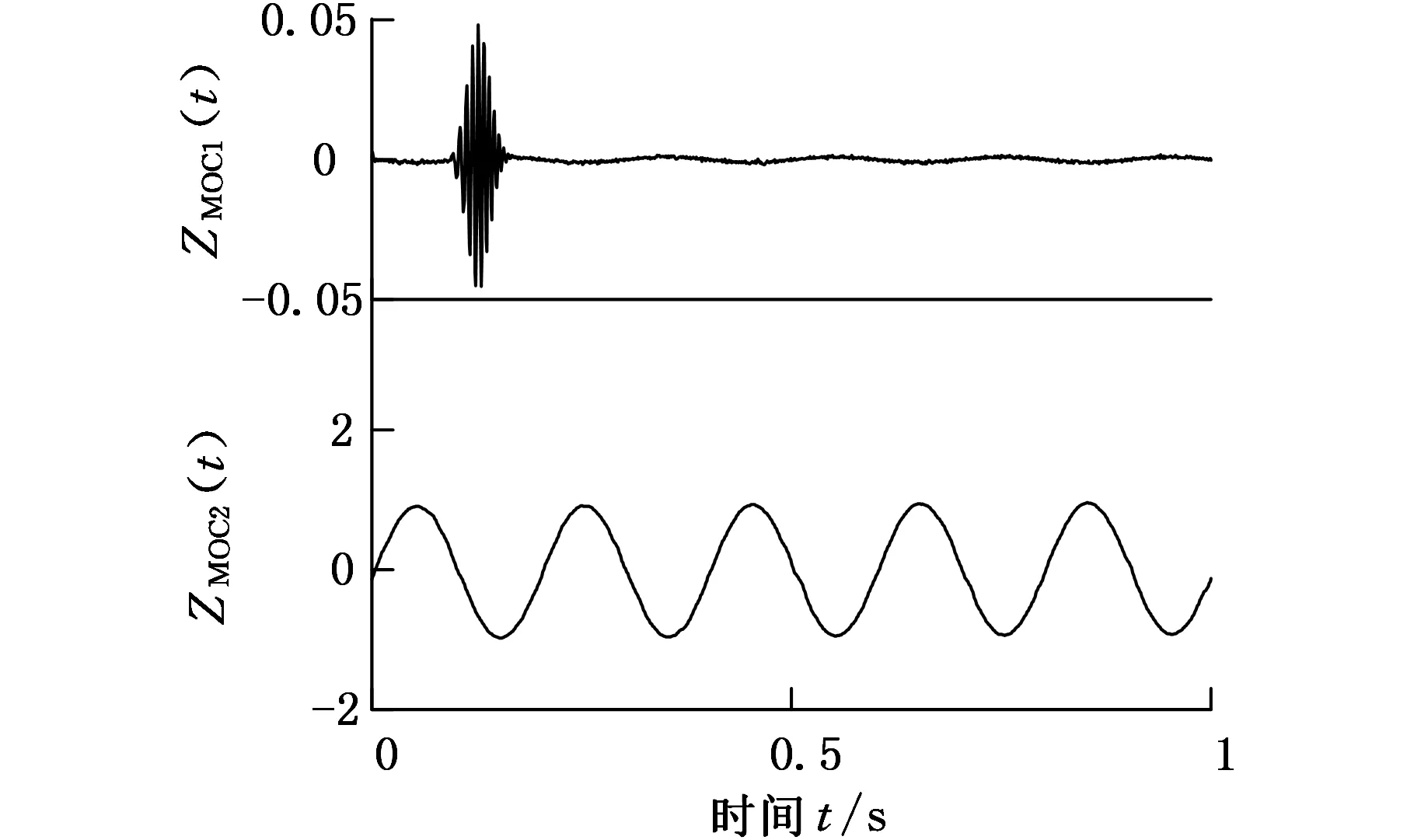
圖4 改進后LOD方法分解仿真信號結(jié)果
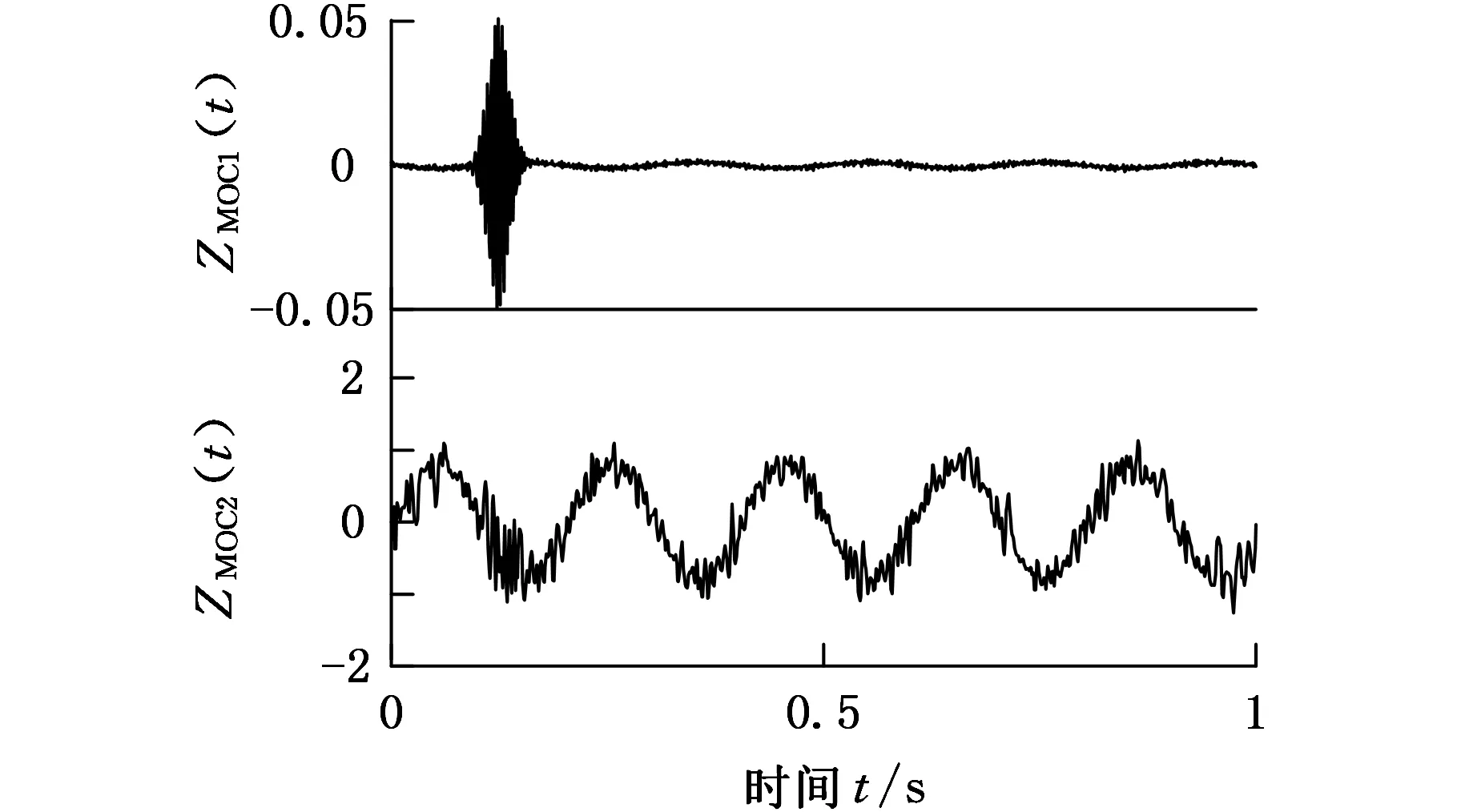
圖5 直接添加白噪聲的分解結(jié)果
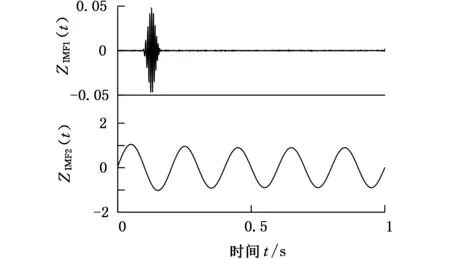
圖6 EEMD方法分解仿真信號結(jié)果

2 齒輪系統(tǒng)的動力學(xué)模型
2.1 齒輪裂紋的時變嚙合剛度計算
時變嚙合剛度作為齒輪系統(tǒng)的主要激勵,其嚙合剛度的變化勢必會引起齒輪系統(tǒng)參數(shù)變化。下面通過材料力學(xué)方法將實驗臺齒輪簡化為變截面的懸臂梁,其齒根裂紋的彎曲變形模型如圖7所示。通過由懸臂梁彎曲剪切變形δ1、基體變形δ2和接觸變形δ3組成的綜合彈性變形即可求出相應(yīng)的嚙合剛度。齒輪參數(shù)如表1所示。
三種變形參數(shù)δ1δ2δ3的計算公式分別如下所示:
(1)

圖7 齒根裂紋彎曲變形模型

模數(shù)(mm)2.5齒頂系數(shù)0.25齒數(shù)37變形系數(shù)0齒寬(mm)20彈性模量(GPa)209齒形角(°)20泊松比0.3齒頂高系數(shù)1
(2)
(3)
(4)
(5)
式中,F(xiàn)為嚙合作用力;αm為實際壓力角;G為剪切模量;Sh為剪切因子;E為楊氏模量;v為泊松比;Ai和Ii分別為有效截面積和慣性矩;W為齒寬;參數(shù)L*、M*、P*、Q*、uf、sf由文獻[14]計算方法可得。
綜上所述,單對齒輪嚙合的有效剛度表示為
(6)
式中,下標(biāo)p、g分別表示主動輪和從動輪。
基于上述分析,求取不同裂紋故障程度下的齒輪時變嚙合剛度,其結(jié)果如圖8所示。
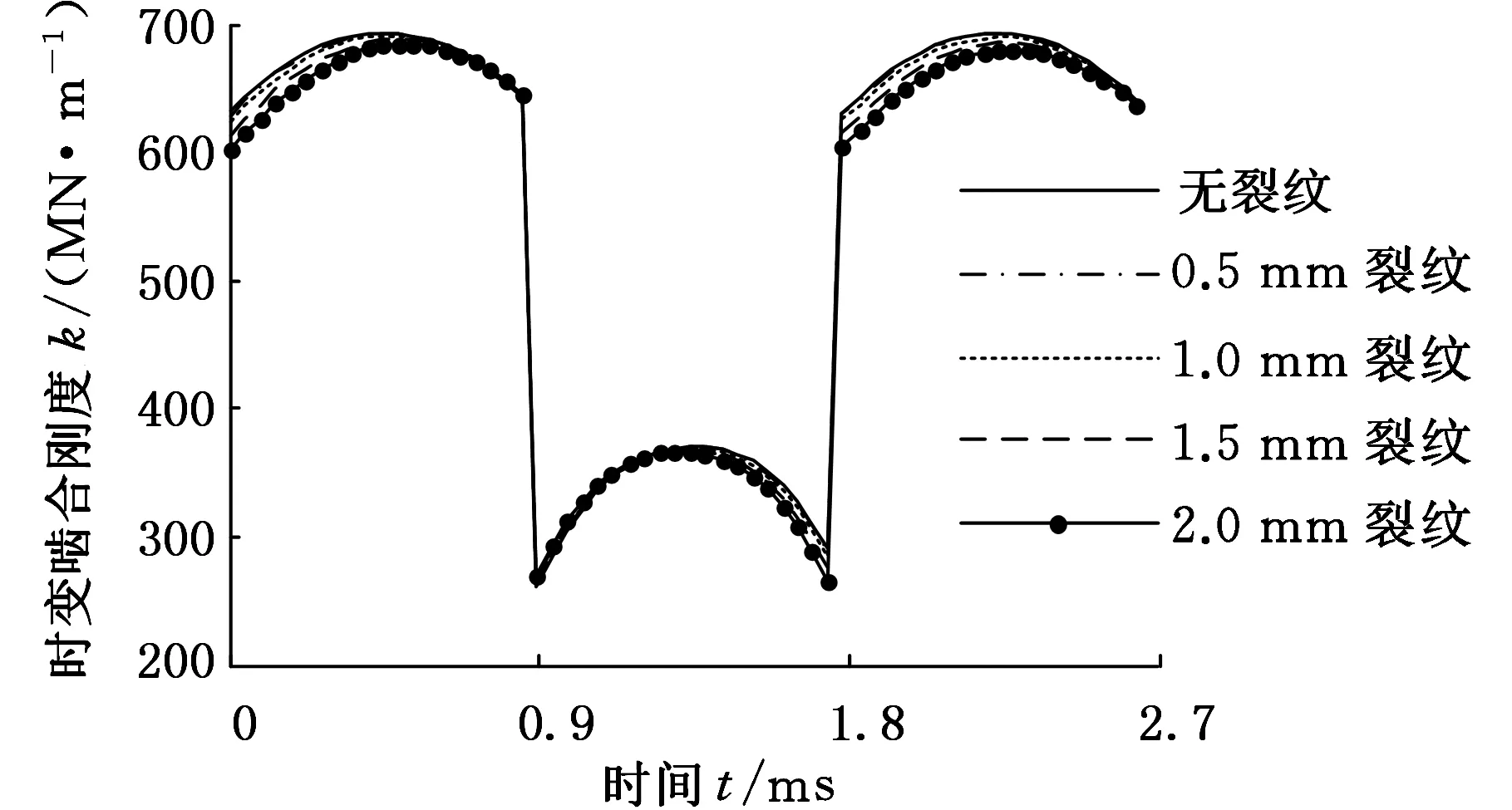
圖8 齒輪時變嚙合剛度變化趨勢
2.2 齒輪裂紋動力學(xué)響應(yīng)的計算
依照圖9所示的旋轉(zhuǎn)機械故障試驗臺,建立六自由度的齒輪系統(tǒng)動力學(xué)模型,如圖10所示。該模型假設(shè)嚙合無誤差,無制造和裝配誤差,并且潤滑效果良好,在所建立的坐標(biāo)系中,y軸平行于嚙合線;x軸平行于齒輪嚙合時因滑動產(chǎn)生的摩擦力方向。

圖9 旋轉(zhuǎn)機械故障試驗臺

圖10 齒輪系統(tǒng)的動力學(xué)模型
通過以上動力學(xué)模型簡圖,構(gòu)建齒輪-轉(zhuǎn)子-軸承系統(tǒng)的動力學(xué)數(shù)學(xué)模型:
(7)
式中,mi為齒輪質(zhì)量;Cij為軸承的阻尼系數(shù);kij為支撐軸承的剛度系數(shù),i=p,g分別表示主動輪和從動輪,j=x,y分別表示坐標(biāo)系中x方向與y方向;FN為齒輪嚙合時的接觸力;Ff為齒輪嚙合狀態(tài)下產(chǎn)生的滑動摩擦力;xi、yi為齒輪平動位移;ji為齒輪轉(zhuǎn)動慣量;θi為齒輪的轉(zhuǎn)動角度;Ti為齒輪所受輸入輸出扭矩;M為感應(yīng)力矩,分別由嚙合線上的齒輪嚙合力與滑動摩擦力組合生成[15];Rbi為齒輪的基圓半徑;k(t)為齒輪時變嚙合剛度;Cm為齒輪嚙合黏性阻尼;μ為齒輪滑動摩擦因數(shù)。
整個旋轉(zhuǎn)機械故障試驗臺設(shè)計參數(shù)如表2所示。

表2 旋轉(zhuǎn)機械故障試驗臺設(shè)計參數(shù)
結(jié)合2.1節(jié)提供的不同裂紋程度下齒輪時變嚙合剛度k(t),采用Runge-Kutta方法求解動力學(xué)方程得到不同裂紋故障程度下的齒輪系統(tǒng)動力學(xué)響應(yīng),如圖11所示。
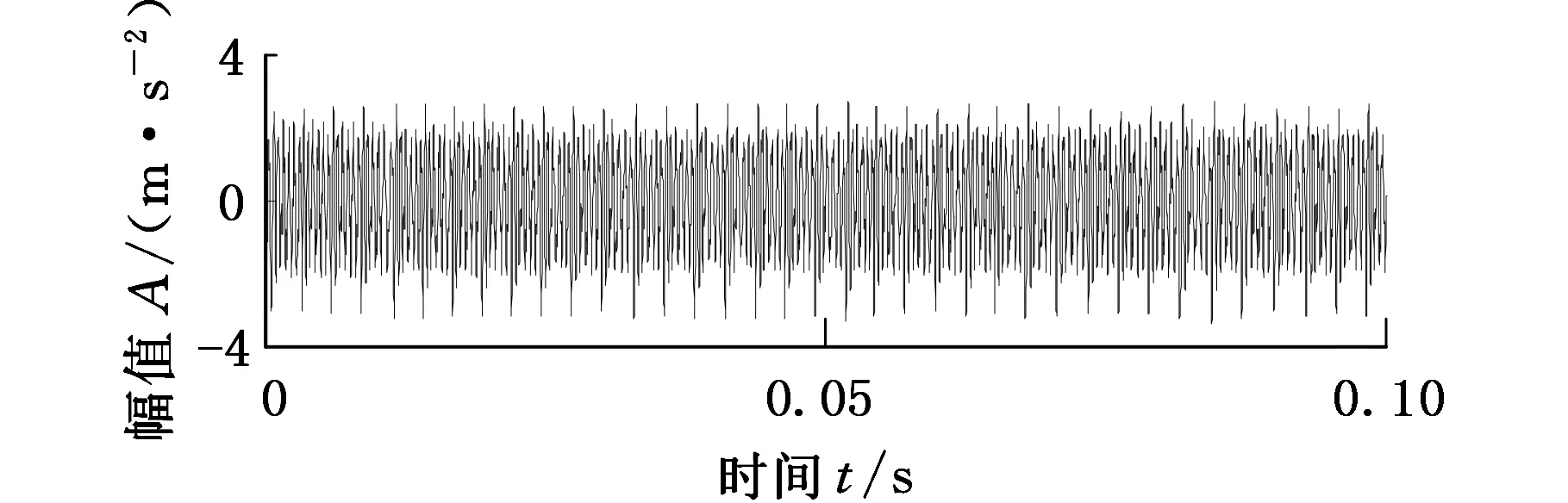
(a)齒輪無裂紋仿真信號時域波形
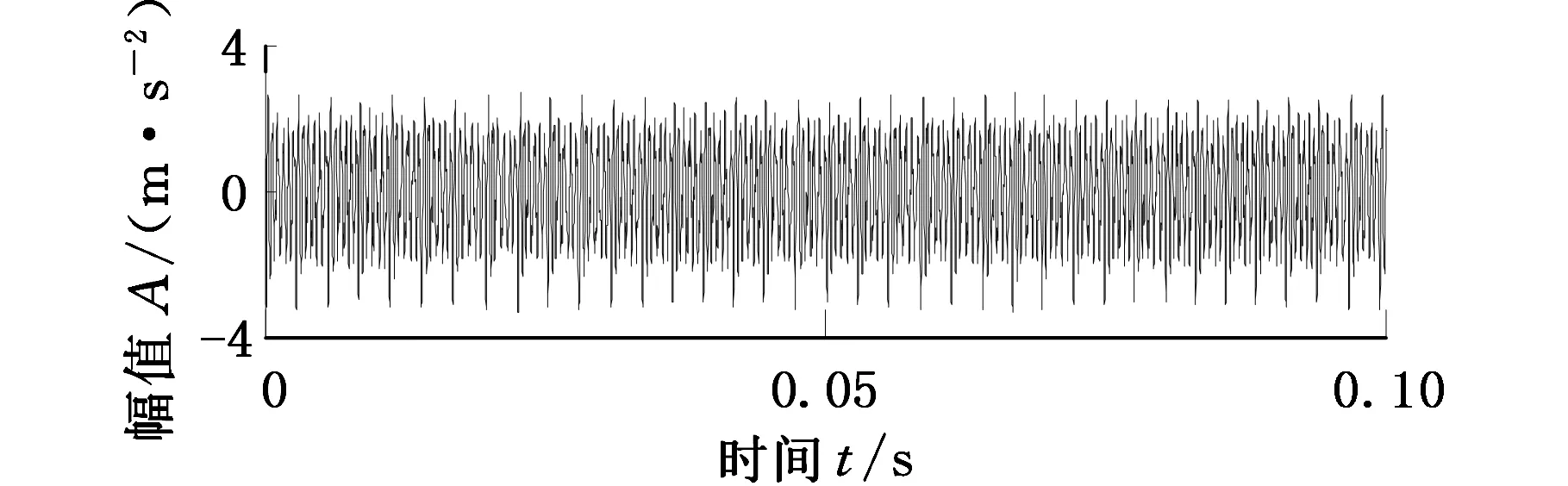
(b)齒輪0.5 mm裂紋仿真信號時域波形
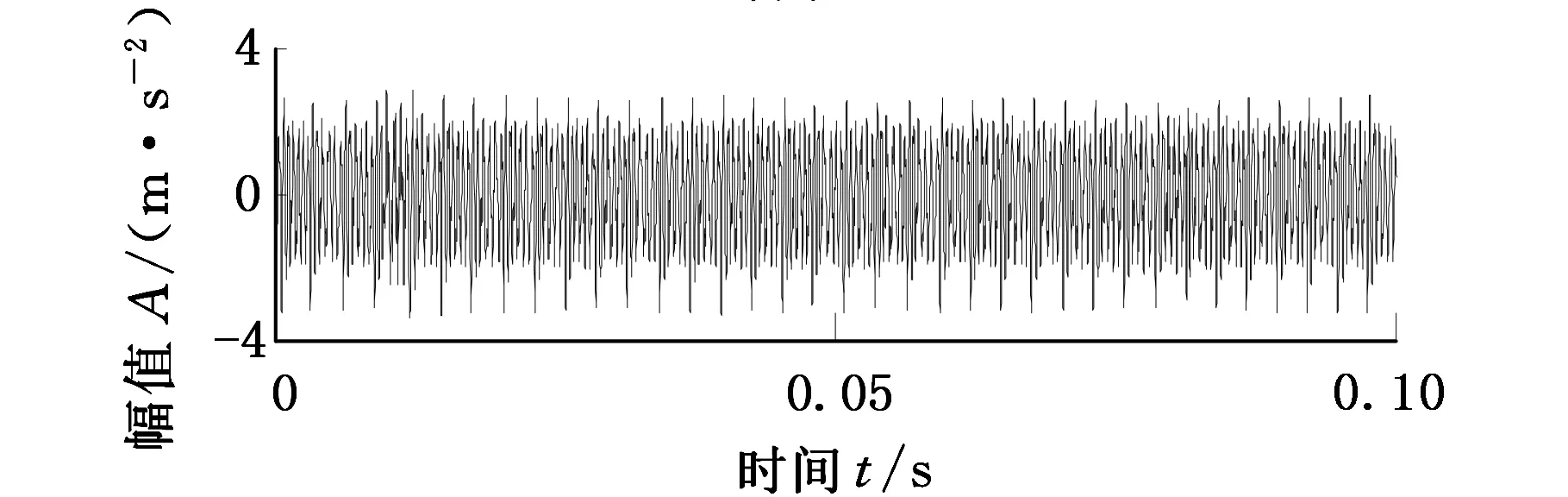
(c)齒輪1.0 mm裂紋仿真信號時域波形
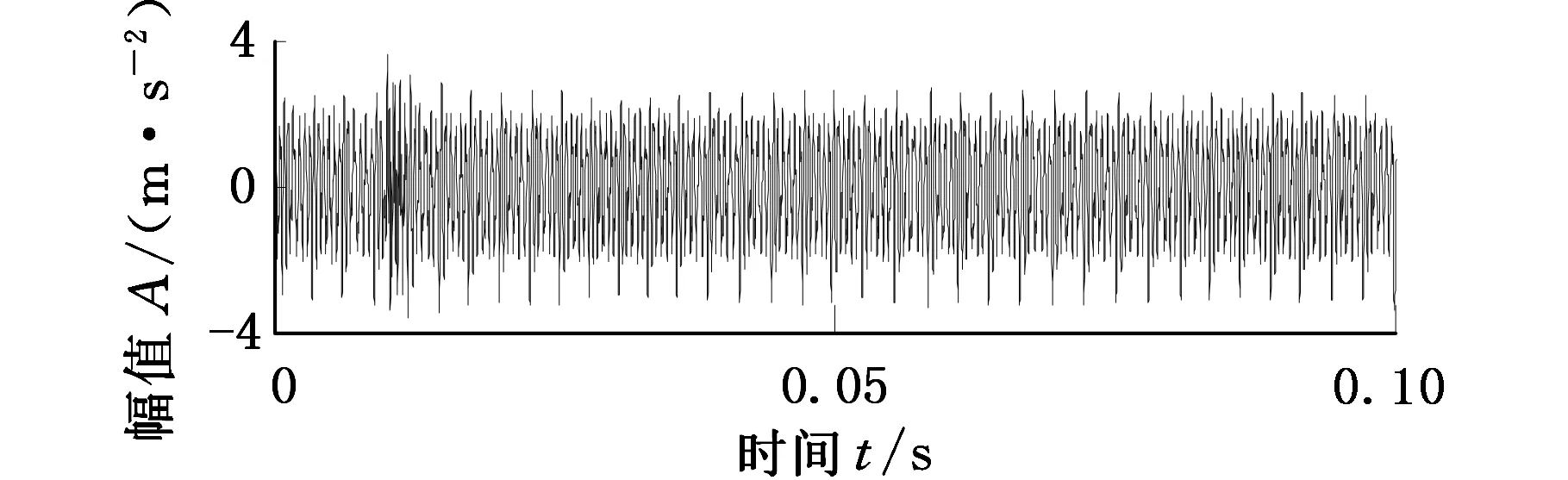
(d)齒輪1.5 mm裂紋仿真信號時域波形

(e)齒輪2.0 mm裂紋仿真信號時域波形圖11 不同裂紋程度的齒輪在一個旋轉(zhuǎn)周期的仿真信號
3 齒根裂紋故障定量診斷分析
3.1 仿真信號分析
已知齒輪的裂紋程度是以時變嚙合剛度作為激勵,反映在動力學(xué)模型中的加速度振動信號上,而統(tǒng)計特征通常被用來描述系統(tǒng)振動趨勢及幅度的大小。考察按第2節(jié)計算方式所得到的齒輪裂紋動力學(xué)響應(yīng)(圖11),采用對故障敏感而不受轉(zhuǎn)速、負(fù)載等條件影響的量綱一參數(shù):峭度指標(biāo)(Ku)、峰值因子(CF)、能量(E)來表征裂紋故障程度。圖12為動力學(xué)響應(yīng)裂紋程度變化的參數(shù)指標(biāo)示意圖。由12圖可知:指標(biāo)參數(shù)隨著裂紋的加深而逐漸增大,峭度指標(biāo)表現(xiàn)出很高的穩(wěn)定性,且對裂紋深度的變化相對敏感;峰值因子在裂紋加深到一定程度后便具有較高的敏感性;能量值在齒輪裂紋深度變化的過程中一直保持良好的敏感性。

圖12 齒輪動力學(xué)響應(yīng)隨裂紋程度變化的Ku、CF、E指標(biāo)
提取20組不同裂紋程度下動力學(xué)模型響應(yīng)信號的峭度指標(biāo)、峰值因子、能量值作為特征參數(shù)構(gòu)建特征向量矩陣作為輸入,齒輪裂紋程度作為輸出,輸入到SVR分類器中以獲得統(tǒng)計特征參數(shù)對應(yīng)裂紋程度的映射關(guān)系。分類器選擇徑向基函數(shù)作為核函數(shù),核函數(shù)參數(shù)ε及C采用遺傳算法優(yōu)化以提高故障診斷準(zhǔn)確率。
3.2 實驗信號分析
旋轉(zhuǎn)機械實驗臺如圖9所示。齒輪系統(tǒng)與動力學(xué)仿真模型參數(shù)相同,均是模數(shù)為2.5 mm、齒數(shù)為37的標(biāo)準(zhǔn)直齒輪,通過人工在齒根切割0.3~1.5 mm深度的裂紋以模擬齒輪根部裂紋故障。實驗時輸入軸轉(zhuǎn)速為600 r/min,轉(zhuǎn)頻fr=10 Hz,嚙合頻率fs=370 Hz。圖13所示為采集到的5種不同裂紋程度的齒輪振動加速度信號的時域波形,采樣頻率為1024 Hz。
振動信號經(jīng)過分解后,沖擊成分由于調(diào)制原因大部分分布在高頻MOC分量中,根據(jù)特征指標(biāo)最大原則選取分量ZMOC1(t)作為裂紋損傷特征頻帶。因此,在實驗信號中隨機選取每類裂紋的5組數(shù)據(jù)作為測試樣本,對每類裂紋狀態(tài)每組

圖13 齒輪裂紋振動加速度信號
齒輪振動加速度信號進行噪聲輔助LOD分解,其分解結(jié)果如圖14~圖16所示(由于篇幅原因只列出0.3 mm、0.75 mm、1.5 mm裂紋振動信號分解后的前5個分量)。分別計算各自ZMOC1(t)分量的峭度指標(biāo)、峰值因子、能量值,構(gòu)建特征向量矩陣并將其輸入到根據(jù)動力學(xué)建模所得到的映射關(guān)系中,進行齒輪裂紋故障診斷,結(jié)果如表3所示。

圖14 齒輪0.3 mm深的裂紋實驗信號的噪聲輔助LOD分解結(jié)果
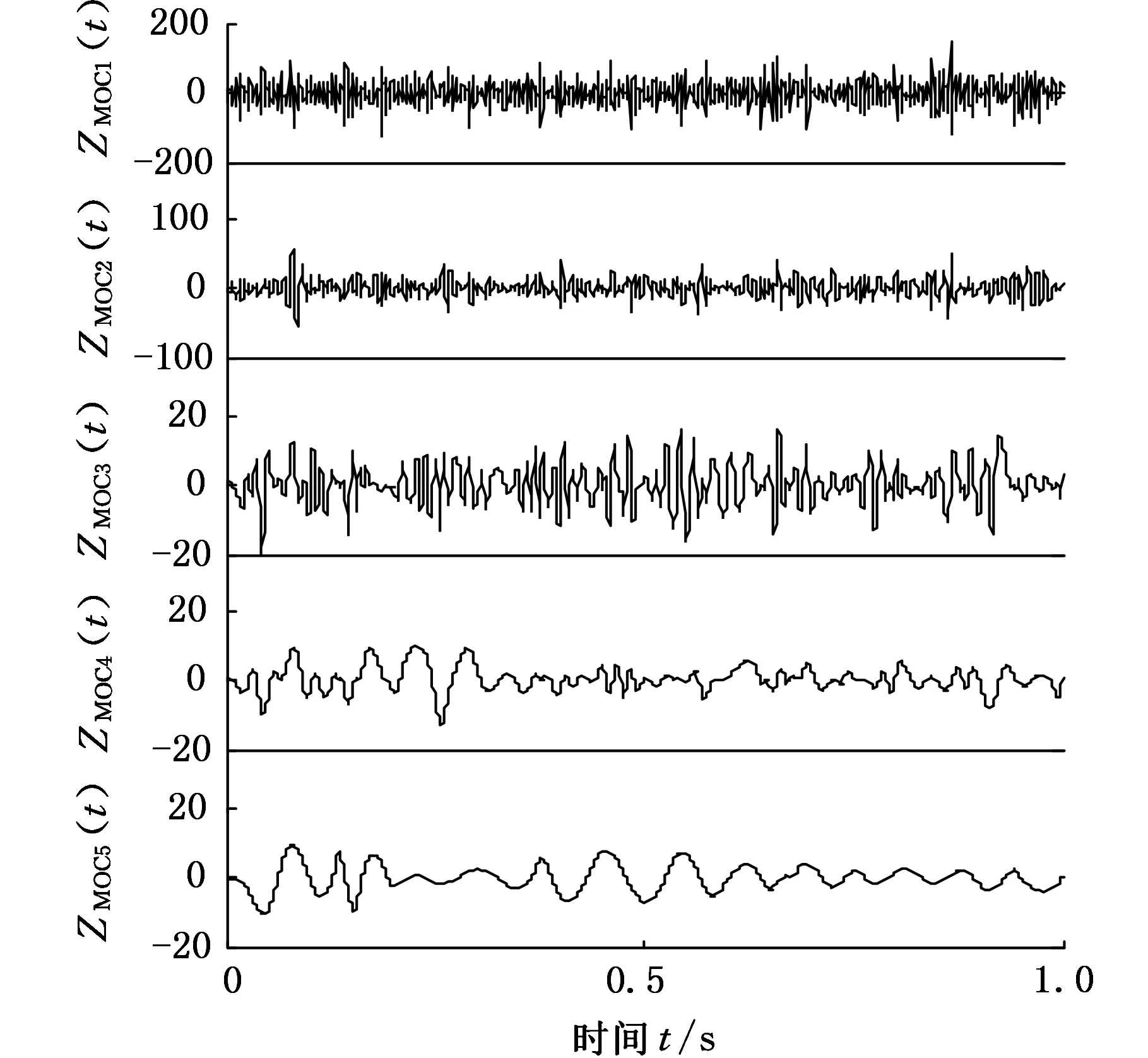
圖15 齒輪0.75 mm深的裂紋實驗信號的噪聲輔助LOD分解結(jié)果
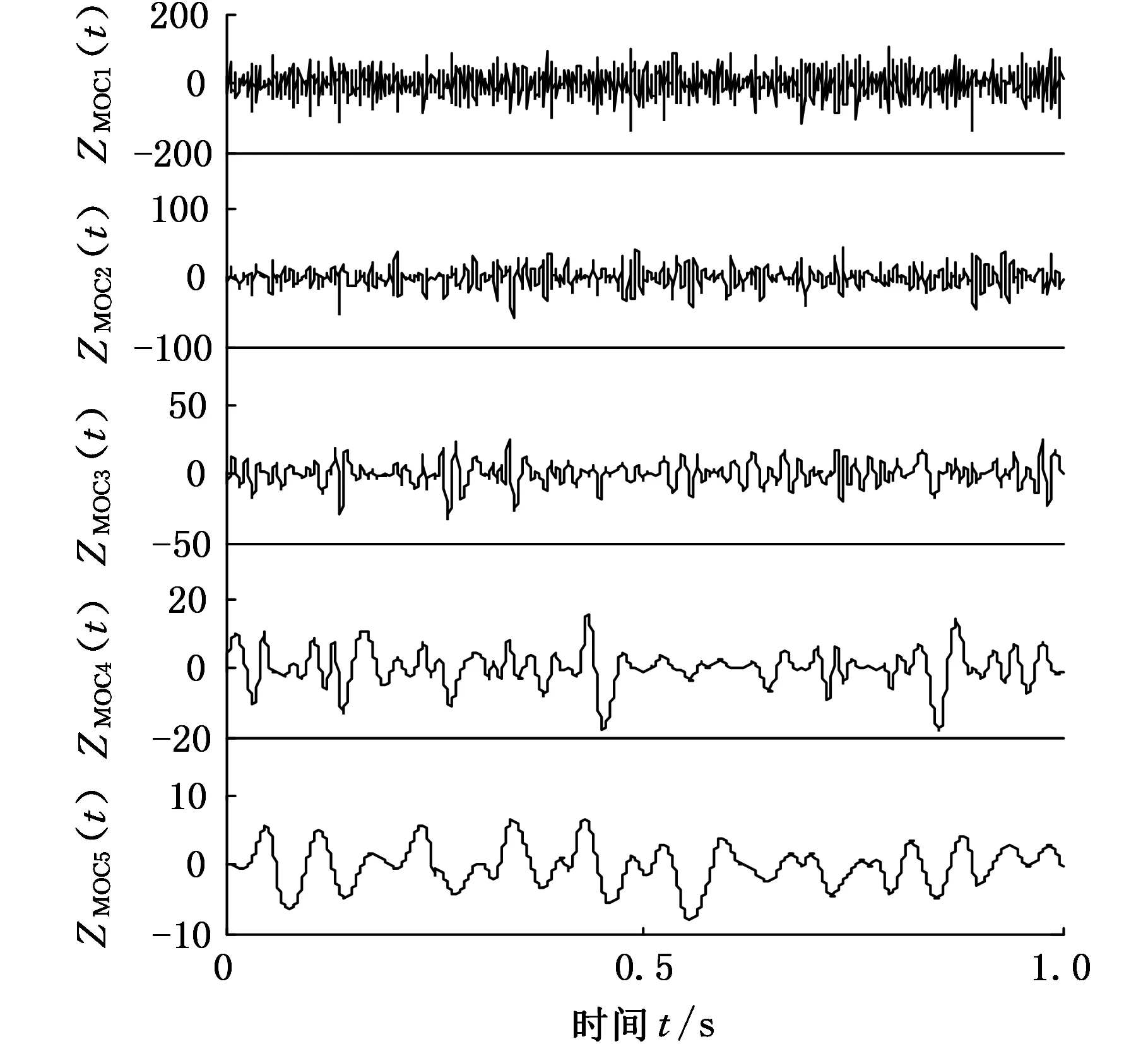
圖16 齒輪1.5 mm深的裂紋實驗信號的噪聲輔助LOD分解結(jié)果
為了驗證本文方法的優(yōu)越性,將改進的LOD方法同未經(jīng)過處理的原始信號和經(jīng)過EEMD方法處理的信號做對比分析。6種不同裂紋齒輪振動加速度信號經(jīng)過EEMD分解,將計算分量ZIMF1(t)的三個指標(biāo)作為特征參數(shù)構(gòu)建成新的特征向量矩陣并輸入到訓(xùn)練后的SVR分類器中。同時,取迭代中止條件SD為0.5,將改進的LOD方法及EEMD方法處理6種齒輪裂紋實驗信號的過程在同一臺計算機上各運行50次,改進LOD

表3 6種裂紋齒輪診斷結(jié)果
方法獲得6種裂紋信號第一個分量的平均時間和EEMD方法處理6種裂紋信號得到第一個分量的平均時間如表3所示。從表3可以看出,經(jīng)過加噪LOD處理后的齒輪裂紋診斷結(jié)果比EEMD方法處理后的準(zhǔn)確率高,且分解時間遠(yuǎn)遠(yuǎn)小于EEMD方法,通過對比可知,改進的LOD方法在準(zhǔn)確性及運算速度上要優(yōu)于EEMD方法,更適合齒輪運行狀態(tài)實時監(jiān)測及故障診斷。
4 結(jié)論
(1)針對LOD方法中存在的模態(tài)混淆問題,提出了一種改進的LOD方法。仿真信號分析結(jié)果表明,基于噪聲輔助的LOD方法能夠有效地解決模態(tài)混淆問題。通過與EEMD方法的對比,可知改進的LOD方法具有迭代次數(shù)少、算法效率高、分解時間短等優(yōu)勢。
(2)本文以旋轉(zhuǎn)機械實驗臺為原形建立齒輪系統(tǒng)動力學(xué)模型,通過研究齒輪動力學(xué)模型對齒輪裂紋故障特征參數(shù)的影響,從齒輪故障機理的角度建立了齒輪裂紋程度與故障特征參數(shù)之間的映射關(guān)系。
(3)基于上述映射關(guān)系,引入噪聲輔助LOD方法提取故障特征實現(xiàn)了齒輪裂紋的定量診斷,實驗結(jié)果表明,本文方法能夠有效地對齒輪裂紋程度進行定量診斷。
[1] Jia S, Howard I. Comparison of Localised Spalling and Crack Damage from Dynamic Modelling of Spur Gear Vibrations[J]. Mechanical Systems & Signal Processing, 2006, 20(2):332-349.
[2] Zhou X,Shao Y, Lei Y, et al. Time-varying Meshing Stiffness Calculation and Vibration Analysis for a 16 DOF Dynamic Model with Linear Crack Growth in a Pinion[J]. Journal of Vibration & Acoustics, 2012, 134(1):192-197.
[3] Shao Y, Chen Z. Dynamic Features of Planetary Gear Set with Tooth Plastic Inclination Deforma-tion Due to Tooth Root Crack[J]. Nonlinear Dynamics, 2013, 74(4):1253-1266.
[4] Chen Z,Shao Y. Dynamic Simulation of Spur Gear with Tooth Root Crack Propagating along Tooth Width and Crack Depth[J]. Engineering Failure Analysis, 2011, 18(8):2149-2164.
[5] Shao Y, Chen Z. Dynamic Features of Planetary Gear Set with Tooth Plastic Inclination Deforma-tion Due to Tooth Root Crack[J]. Nonlinear Dynamics, 2013, 74(4):1253-1266.
[6] Rincon A F D,Viadero F, Iglesias M, et al. A Model for the Study of Meshing Stiffness in Spur Gear Transmissions[J]. Mechanism & Machine Theory, 2013, 61:30-58.
[7] 于德介,程軍圣,楊宇.Hilbert-Huang變換在齒輪故障診斷中的應(yīng)用[J].機械工程學(xué)報,2005,41(6):102-107. Yu Dejie, Cheng Junsheng, Yang Yu. Application of Hilbert-Huang Transform Method to Gear Fault Diagnosis[J]. Journal of Mechanical Engineering, 2005,41(6):102-107.
[8] 程軍圣,楊宇,于德介.局部均值分解方法及其在齒輪故障和診斷中的應(yīng)用[J].振動工程學(xué)報,2009,22(1):76-84. Cheng Junsheng, Yang Yu, Yu Dejie. The Local Mean Decomposition Method and Its Application to Gear Fault Diagnosis[J].Journal of Vibration Engineering,2009,22(1):76-84.
[9] Pegram G G S, Peel M C, Mcmahon T A. Empirical Mode Decomposition Using Rational Splines: an Application to Rainfall Time Series[J]. Proceedings of the Royal Society A, 2008, 464:1483-1501.
[10] Bao C, Hao H, Li Z X, et al. Time-varying System Identification Using a Newly Improved HHT Algorithm[J]. Computers & Structures, 2009, 87(23/24):1611-1623.
[11] 張亢, 廖力達(dá), 吳家騰. 一種新的非平穩(wěn)信號分析方法-局部波動特征分解[C]// 全國設(shè)備監(jiān)測診斷與維護學(xué)術(shù)會議、全國設(shè)備故障診斷學(xué)術(shù)會議暨2014年全國設(shè)備診斷工程會議.秦皇島,2014:470-473.
[12] 張亢, 吳家騰, 廖力達(dá). 局部波動特征分解及其在齒輪包絡(luò)分析中的應(yīng)用[J]. 振動工程學(xué)報, 2015, 28(5):846-854. Zhang Kang, WuJiateng, Liao Lida. Local Oscillatory-characteristic Decomposition and Its Applicat-ion to Gear Envelope Analysis[J]. Journal of Vibration Engineering, 2015, 28(5):846-854.
[13] Flandrin P, Rilling G, Goncalves P. Empirical Mode Decomposition as a Filter Bank[J]. IEEE Signal Processing Letters, 2004, 11(2):112-114.
[14] Chaari F, Fakhfakh T, Haddar M. Analytical Modelling of Spur Gear Tooth Crack and Influence on Gearmesh Stiffness[J]. European Journal of Mechanics-A/Solids, 2009, 28(3):461-468.
[15] He S, Cho S, Singh R. Prediction of Dynamic Friction Forces in Spur Gears Using Alternate Sliding Friction Formulations[J]. Journal of Sound & Vibration, 2008, 309(3/5):843-851.
(編輯 王旻玥)
作者簡介:吳家騰,男,1990年生。湖南大學(xué)機械與運載工程學(xué)院博士研究生。主要研究方向為設(shè)備狀態(tài)監(jiān)測及診斷。彭曉燕(通信作者),女,1965年生。湖南大學(xué)機械與運載工程學(xué)院教授、博士研究生導(dǎo)師。楊 宇,女,1971年生。湖南大學(xué)機械與運載工程學(xué)院教授、博士研究生導(dǎo)師。張 亢,男,1984年生。長沙理工大學(xué)能源與動力工程學(xué)院講師。程軍圣,男,1968年生。湖南大學(xué)機械與運載工程學(xué)院教授、博士研究生導(dǎo)師。
Quantitative Diagnosis Method of Gear Cracks Based on Noise-assisted LOD
Wu Jiateng1Peng Xiaoyan1Yang Yu1Zhang Kang2Cheng Junsheng1
1.State key Laboratory of Advanced Design and Manufacture for Vehicle Body,Hunan University, Changsha, 410082 2.Changsha University of Science and Technology, Changsha, 410076
A new method of quantitative diagnosis of gear crack faults was proposed based on noise-assisted LOD which combined gear fault mechanism with fault diagnosis methods. Firstly, the feature vector matrixes were constituted by feature parameters which sensitively and independent of working conditions might be extracted from a dynamics model established to obtain the dynamics responses under different levels of cracks and input into the support vector regression(SVR),thus the mapping relationship among feature parameters and levels of gear cracks was created. Based on mapping relationship, the quantitative diagnosis of gear cracks was realized by using noise-assisted LOD extracting feature parameters from actual gear crack signals.
noise-assisted; local oscillatory-characteristic decomposition(LOD); feature extrac-tion; mapping relationship; quantitative diagnosis of gear crack
2016-01-26
國家自然科學(xué)基金資助項目(51575168,51375152,51305046);國家科技支撐計劃資助項目(2015BAF32B03);智能型新能源汽車協(xié)同創(chuàng)新中心資助項目;湖南省綠色汽車協(xié)同創(chuàng)新中心項目
TN911.7; TH113.1
10.3969/j.issn.1004-132X.2016.23.011
馬永敬,男,1987年生。中車青島四方機車車輛股份有限公司工程師,合肥工業(yè)大學(xué)機械與汽車工程學(xué)院博士研究生。研究方向為制造過程監(jiān)測與控制、數(shù)字化工廠。劉明周,男,1968年生。合肥工業(yè)大學(xué)機械與汽車工程學(xué)院教授、博士研究生導(dǎo)師。文 勃,男,1966年生。中車青島四方機車車輛股份有限公司高級工程師。凌 琳,男,1987年生。合肥工業(yè)大學(xué)機械與汽車工程學(xué)院講師、博士。

