液壓缸非線性剛度作用下的軋機輥系振動行為及控制

劉 彬 李 鵬 劉 飛 劉浩然 姜甲浩

燕山大學，秦皇島,066004

?

液壓缸非線性剛度作用下的軋機輥系振動行為及控制

劉 彬 李 鵬 劉 飛 劉浩然 姜甲浩

燕山大學，秦皇島,066004

針對液壓系統動態特性影響下的軋機振動問題，建立一種液壓缸非線性剛度約束下的軋機輥系振動模型，采用平均法求得系統的幅頻響應。在Lyapunov第二方法的基礎上，設計了系統的反饋控制器。以軋機實際參數為例，仿真分析軋機輥系中非線性剛度系數、外激勵和無桿腔初始位移等參數對幅頻響應的影響，并研究外激勵幅值和無桿腔初始位移等參數發生變化時的動態分岔特性，發現隨著這些參數的變化，軋機輥系振動在周期運動、倍周期運動和混沌運動等多種運動狀態之間交替變化；同時在系統中引入反饋控制，通過對比控制前后的時域曲線和相平面曲線，驗證了反饋控制器的有效性。研究結果為提高軋機輥系穩定性提供了理論參考。

軋機振動；幅頻響應；反饋控制器；分岔特性

0 引言

隨著現代工業的快速發展，各行各業對軋制產品的質量和軋制速度提出了更高的要求,而軋機振動成為制約軋制產品快速發展的主要障礙之一。軋機振動的發生給軋制過程帶來很大的危害，嚴重時可能損壞軋機設備，甚至可能造成重大的經濟損失[1]。

軋機振動問題是一個世界難題，各國專家從不同角度進行了研究[2]。Bar等[3]建立了軋機振動系統的數學模型，通過分析非線性參數和軋制速度的相互關系得出，軋制速度的大小直接影響等效阻尼的大小，進而影響系統的自激振動。楊旭等[4]結合軋制工藝潤滑原理和機械振動理論，建立基于輥縫動態摩擦方程的軋機垂直振動模型，分析了變形區混合摩擦狀態，軋輥-軋件表面粗糙度、軋件入口厚度與系統穩定性的關系。范小彬等[5]根據軋制界面非線性黏滑摩擦特性，建立了軋輥水平方向摩擦顫振模型及由不平衡力引起的工作輥水平方向“跳振”模型，發現當外擾力幅較小時系統呈現概周期運動, 外擾力幅較大時系統呈混沌狀態。劉浩然等[6]考慮四輥軋機在軋制過程中液壓壓下缸和平衡缸的分段非線性約束作用，建立了軋機輥系的多分段非線性動力學模型，發現分段非線性因素影響下系統的振動行為是比較復雜的。Tran等[7]認為液壓系統的非線性特性主要體現在由于速度變化引起的液壓元件內部摩擦因數非線性，動態載荷使得液壓元件等效剛度呈非線性變化。液壓系統是軋機系統中非常典型的非線性系統，因此研究液壓系統非線性約束下的軋機振動，對揭示液壓系統動態特性影響下的軋機振動機理有重要價值。

本文考慮軋制過程中液壓系統動態特性的影響，建立一種液壓缸非線性剛度約束下的軋機輥系振動模型,分析各參數對系統幅頻特性和分岔特性的影響，最后引入反饋控制，研究軋機輥系在引入控制前后的穩定性。

1 非線性彈簧力

本文主要考慮一種雙作用單活塞液壓缸約束下的軋機輥系的振動特性，圖1為雙作用單活塞液壓缸的結構圖。該種液壓缸只在活塞的一側裝有活塞桿，因而兩腔的有效面積不同，往返的運動速度和作用力也不相等，液壓缸活塞運動改變了兩腔液體的有效長度，引起了液壓油的剛度的變化。

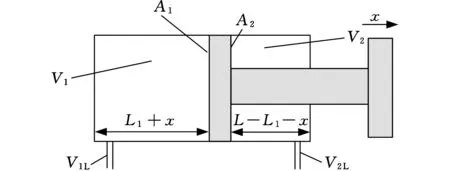
圖1 單活塞液壓缸結構圖

在液壓系統中, 液壓油實際上是以與彈簧大體相同的方式壓縮。液壓缸系統彈簧剛度由活塞桿剛度和液壓油剛度串聯組成。活塞桿的體積模量是液壓油體積模量的近百倍，故可以把活塞桿看作剛體處理，液壓缸的非線性剛度主要由液壓油的剛度決定[8]，其變化規律為[9]

(1)

式中，K為液壓油的體積模量;L為液壓缸的有效行程；Ai為液壓缸活塞兩側的有效面積，i=1,2;L1為無桿腔的初始有效長度;x為系統顫振位移;ViL為閥與缸某一側之間液壓管路中液壓油的體積，i=1,2。

系統液壓缸的彈簧力可以表示為

(2)

由于V1L、V2L與A1(L1+x)、A2(L-L1-x)相比很小，因此液壓缸的彈簧力可以表示為

(3)

由式(3)可以看出，液壓缸的彈簧力隨活塞位置變化呈現非線性，這為研究液壓缸非線性剛度約束下的軋機輥系振動問題提供了理論基礎。

2 軋機輥系振動模型

在軋機垂直振動中，液壓系統的非線性約束作用不可忽略[10]，因此將其等效為彈簧剛度k(x)加入到軋機輥系模型中。考慮到四輥軋機上下輥系沿軋制線對稱[11]，故以上輥系為研究對象，將其等效為一個質量塊的單自由度集中參數模型，建立圖2所示的軋機輥系動力學模型。其中，m為軋機工作輥和支撐輥的等效質量，c為軋機系統的線性阻尼系數，k為軋機系統的線性剛度系數，F為外激勵幅值，τ為引入軋機系統的控制輸入量。本文主要考慮雙作用單活塞液壓缸非線性剛度約束作用，暫不考慮液壓缸和軋機系統的非線性摩擦力。根據廣義耗散拉格朗日原理，建立一種雙作用單活塞液壓缸非線性剛度約束下的軋機系統動力學方程：

(4)

式中，α為液壓缸非線性剛度的約束系數。

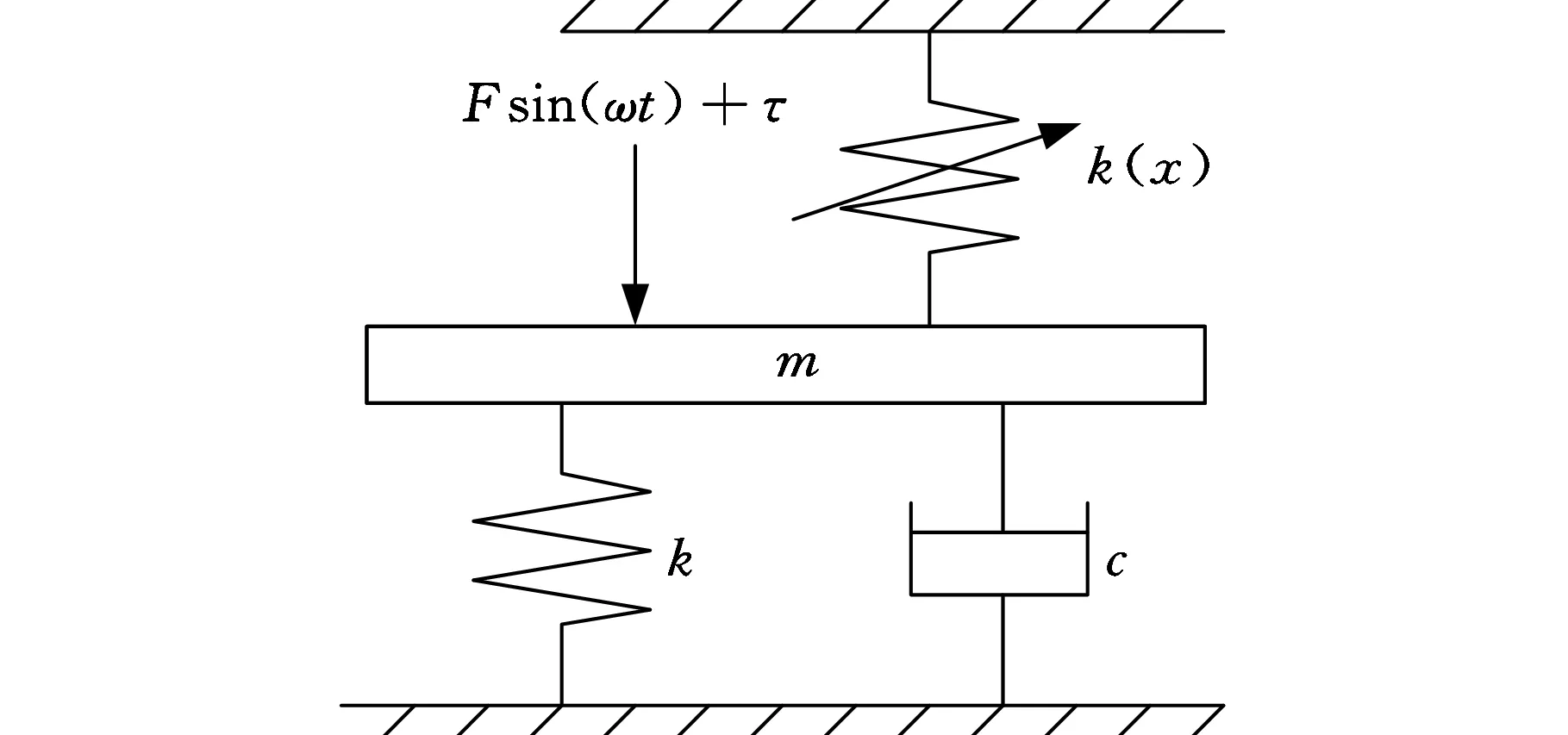
圖2 軋機輥系的動力學模型

該模型考慮了液壓缸非線性剛度k(x)的約束作用，同時引入控制輸入量τ對系統進行反饋控制。

3 幅頻響應求解

為便于計算，將系統動力學方程式(4)簡化成如下形式：

(5)

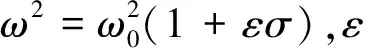
(6)

(7)

令式(6)中的ε=0，導出派生系統的解及其導數：

x=acos(ωt-θ)

(8)

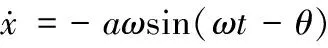
(9)

其中，a和θ為時間的慢變函數，并認為a和θ在一個周期內保持不變，得到平均化方程：

(10)

(11)

其中，φ=ωt-θ。將式(7)代入式(11)得到

F*cosθ+δaω

(12)

(13)

(14)

將式(12)～式(14)代入式(10)可以得到平均化的具體方程：

(15)

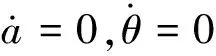
(16)

式(16)即為液壓缸動態特性影響下的軋機輥系的幅頻方程，是進一步研究軋機振動特性的基礎。

4 軋機輥系的穩定性控制

將液壓彈簧力的非線性動態特征歸結為Duffing方程，同時系統中引入控制輸入量，基于Lyapunov穩定判別法給出軋機輥系漸進穩定的條件。

以式(1)所示的液壓缸動態剛度模型為例，對其在原點處進行泰勒級數展開：

(17)

彈簧彈性勢能U具有對稱性，可以表示為

(18)

則彈簧力可以表示為

(19)

將控制輸入量引入軋機輥系模型，可得系統動力學方程

(20)

為了便于分析，將式(20)中的一次項和三次項系數用字母κ1和κ2代替，簡化處理后可得

(21)

本文的控制目的是令式(21)的解為預期函數xd(t)，為達到這個目的，選擇控制輸入為[12]

(22)

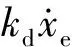
聯立式(21)和式(22)可得動力系統

(23)

由式(23)可以看出，系統的誤差動力瞬間行為是由增益kd和kp的大小決定的。為判定kd和kp的大小，構造如下Lyapunov函數:

(24)

0<λ<δ+kd

(25)

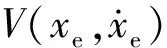
(26)

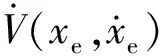
5 數值分析

某廠四輥軋機實際參數為：m=1.44×105kg，c=2.04 MN·s/m，k=23.5 GN/m，L=0.11 m，A1=0.6361 m2，A2=0.3243 m2，K=1.6 GPa，ε=0.01，kd=1.1 kN/m，λ=1.0×103，kp=1.1 MN/m。對軋機輥系振動系統進行數值仿真，分析軋機系統的幅頻特性、分岔特性以及加入控制后的振動特性，研究軋機輥系的振動行為。

5.1 幅頻特性

考慮軋機輥系振動系統受到不同軋制參數的影響，以非線性剛度系數α、無桿腔初始位移L1和外激勵幅值F為研究對象，分析這些參數對軋機輥系振動的影響規律。

由圖3可以看出，α的大小直接影響軋機輥系的固有頻率。隨著非線性剛度系數α的增大，軋機輥系固有頻率減小，系統幅頻曲線向左平移，遠離軋機輥系的共振頻率。同時，α的增大，減小了軋機輥系的振動幅值，有效地減小了外部擾動對軋機輥系振動的影響。

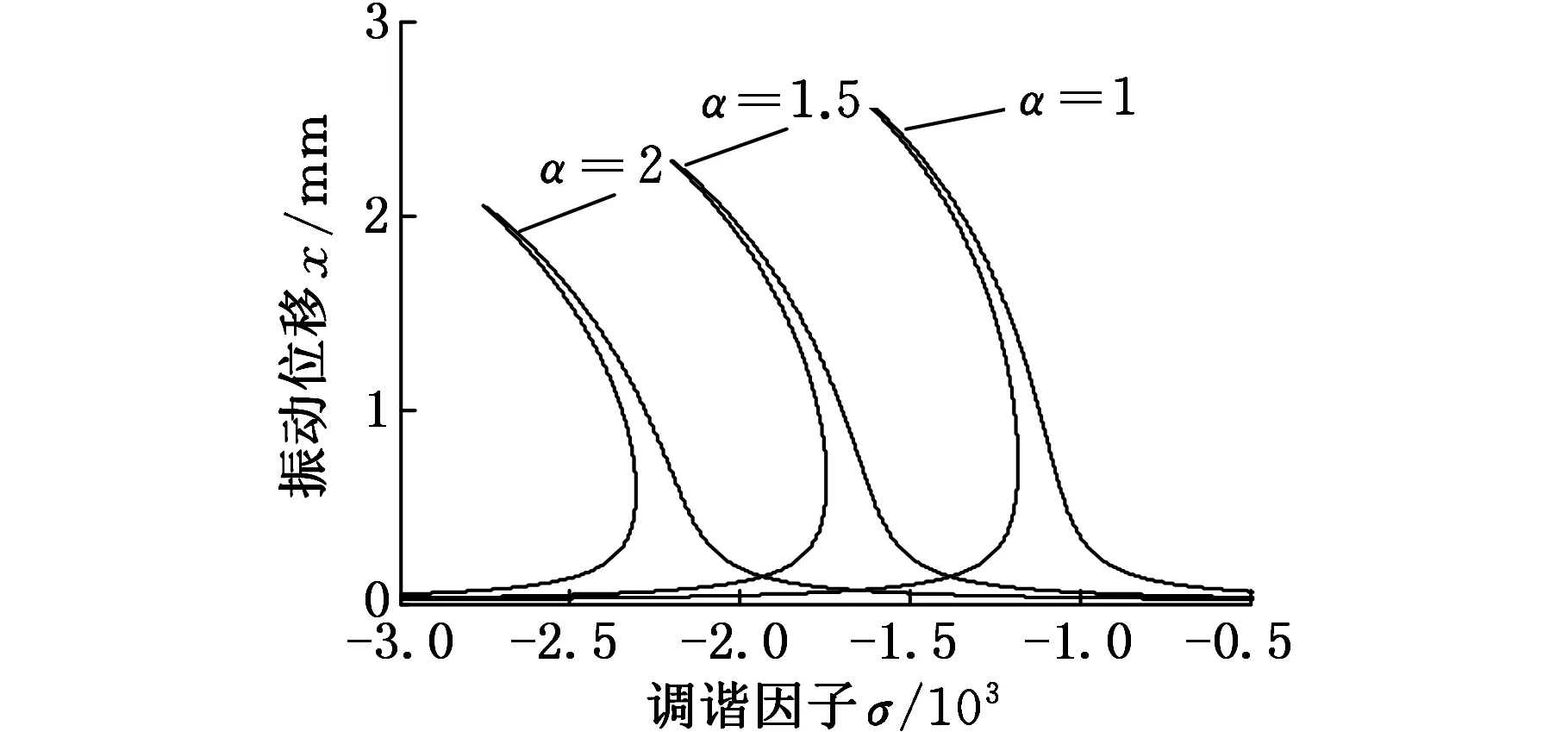
圖3 非線性剛度系數對幅頻特性的影響

從圖4可以發現，系統幅頻特性曲線對無桿腔初始位移L1非常敏感。L1小幅度減小，系統幅頻曲線的拐彎程度明顯增大，軋機輥系的幅頻曲線的跳躍現象變得明顯，系統更易于失穩。因此，適當地控制液壓缸無桿腔初始位移L1位置，有利于軋機輥系的穩定性。

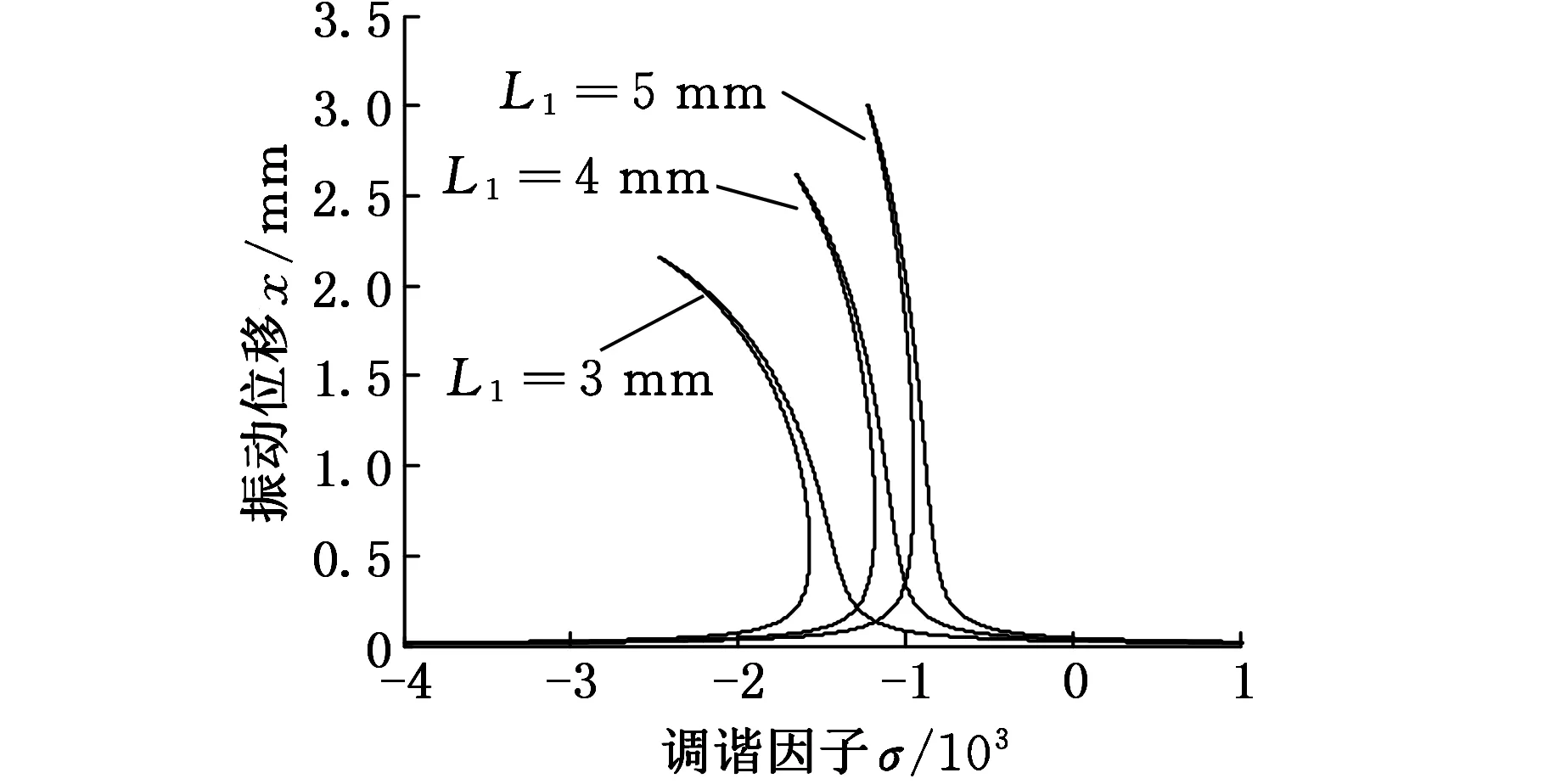
圖4 初始位移對幅頻特性的影響

對比圖5中的三條曲線可以發現，外激勵幅值F的大小直接影響系統振動幅值的大小。外激勵幅值F的增大將使軋機輥系振動幅值增大，同時系統的主共振頻帶變寬，系統的不穩定范圍擴大。

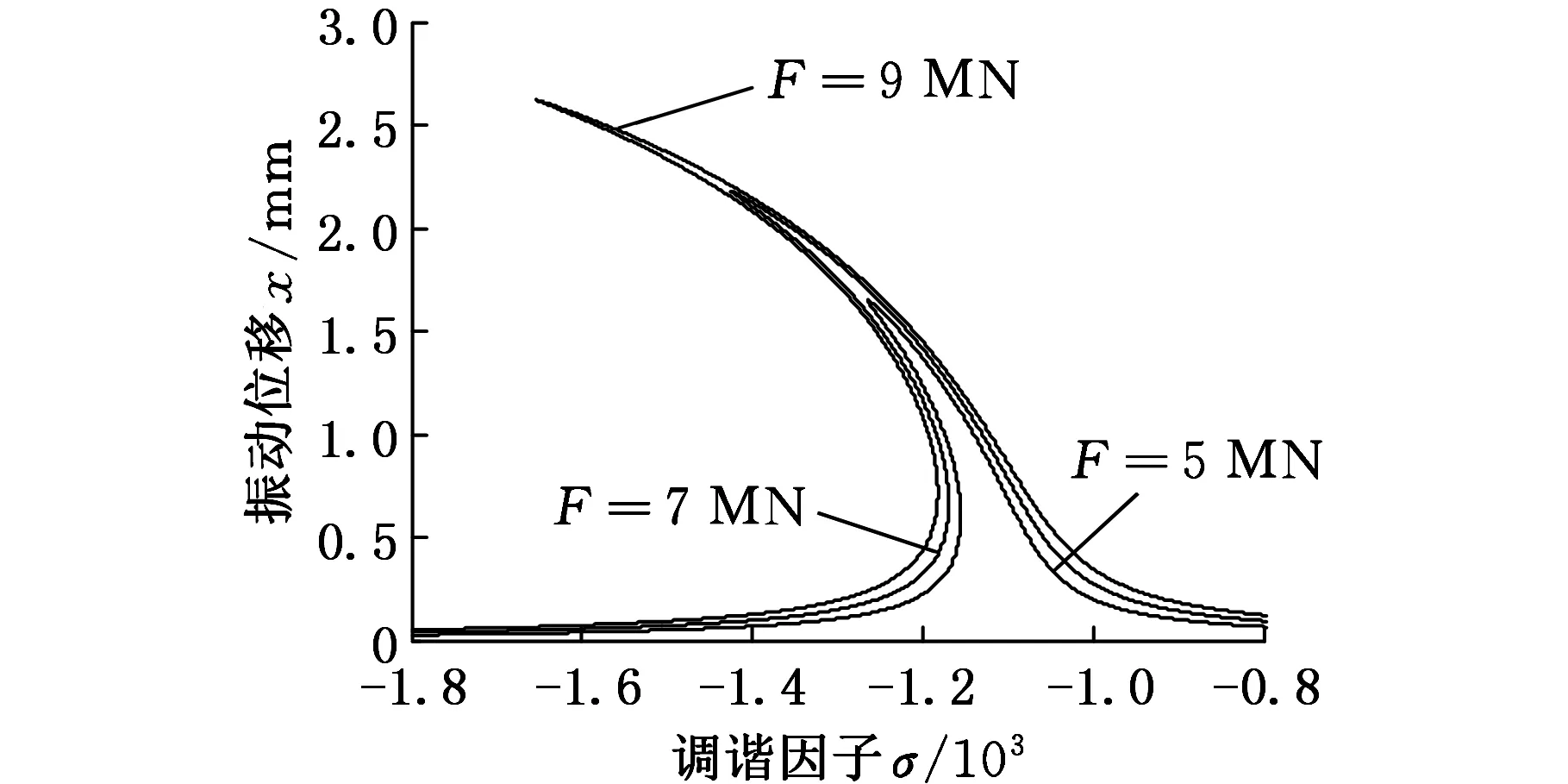
圖5 外激勵幅值對幅頻特性的影響

對比圖3～圖5所示的幅頻特性曲線可以看出，非線性剛度系數、無桿腔初始位移和外激勵幅值等參數的變化影響著幅頻特性的變化，因此可以適當地控制這些參數，有效地降低共振對軋機輥系的危害。

5.2 分岔特性

以液壓缸無桿腔初始位移L1和外激勵幅值F為分岔參數，分析系統分岔響應隨液壓缸無桿腔初始位移L1和外激勵幅值F的變化規律，研究液壓缸無桿腔初始位移L1和外激勵幅值F對系統穩定性的影響。

圖6～圖9所示為液壓缸無桿腔不同初始位移L1時的分岔特性。通過觀察不同初始位移L1的相平面圖和Poincare截面，分析液壓缸非線性剛度約束系統的分岔響應隨初始位移L1的變化規律。

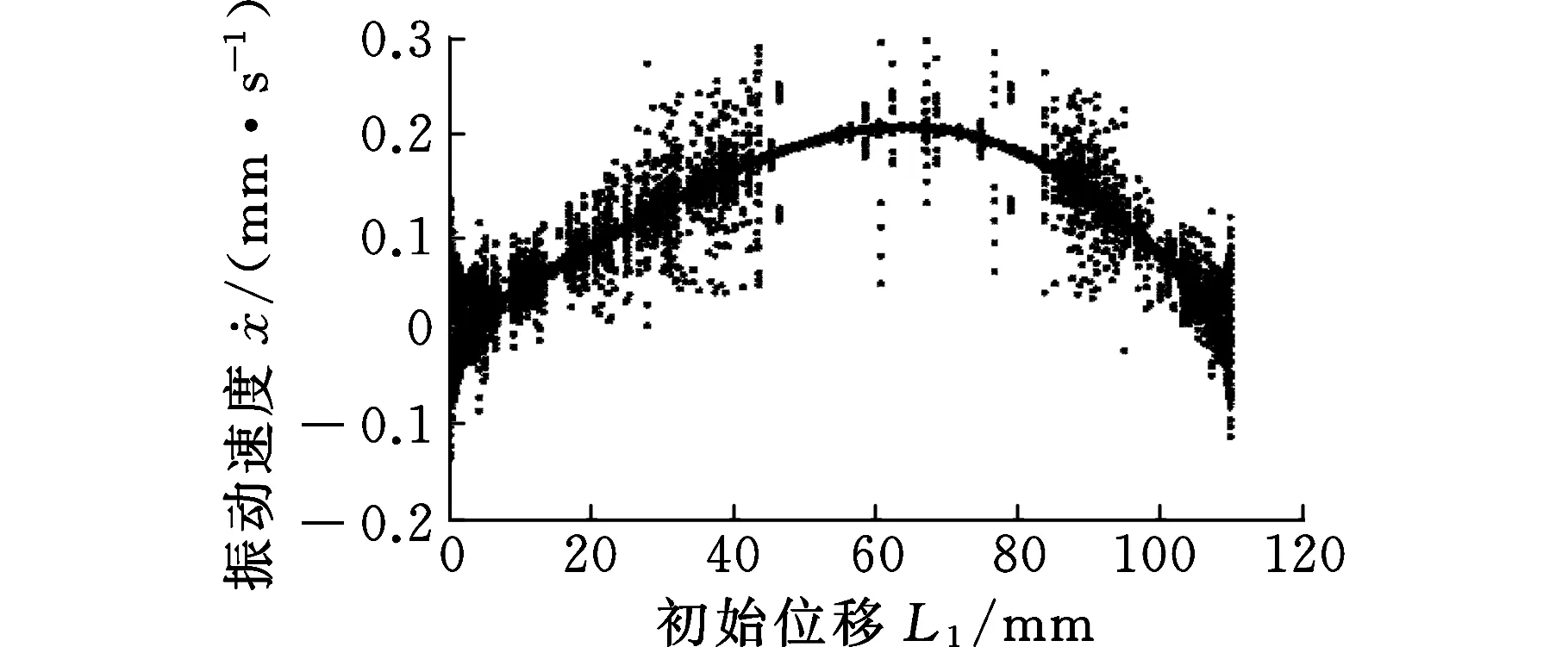
圖6 L1變化時的分岔特性

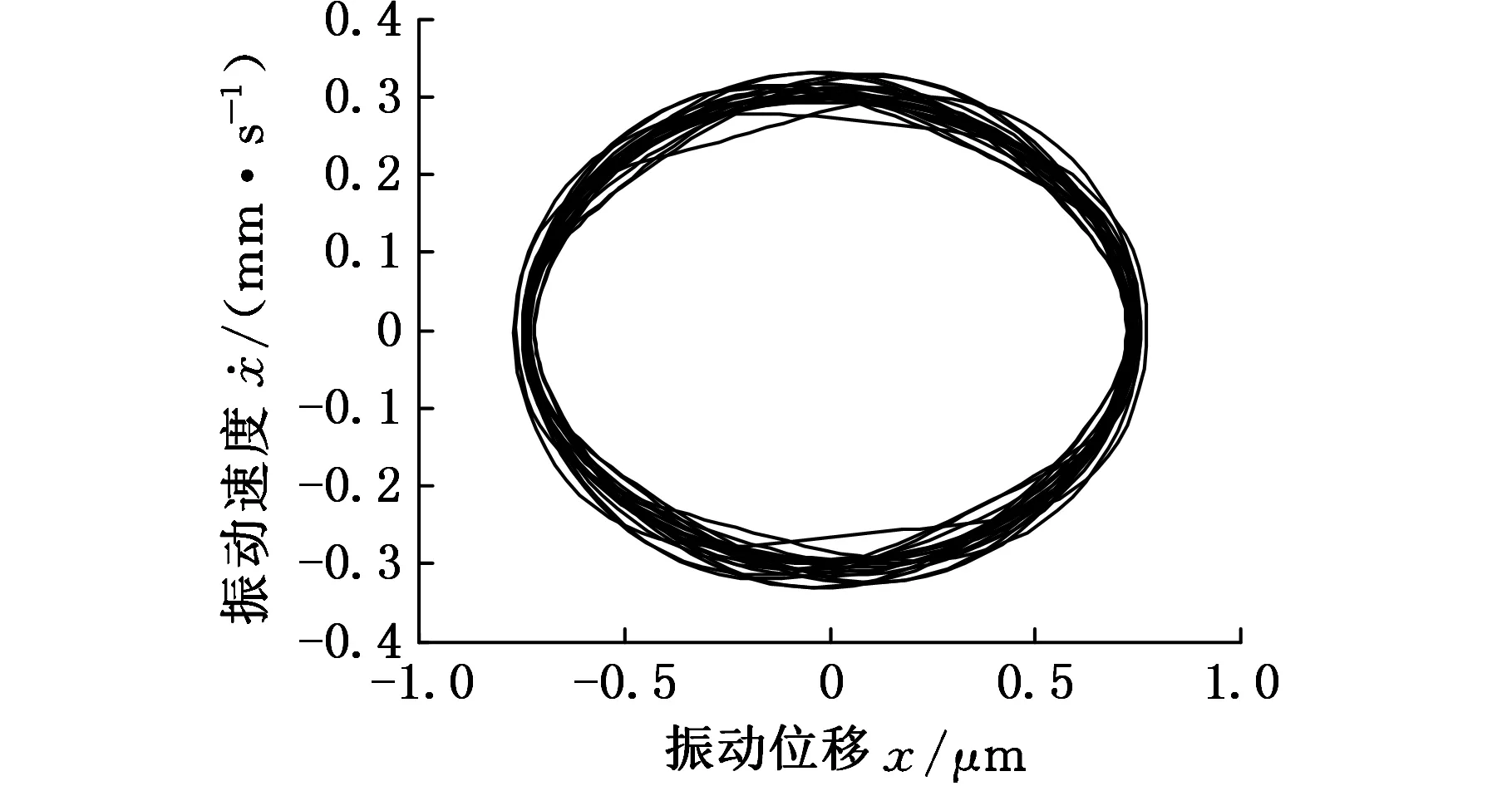
(a)相圖

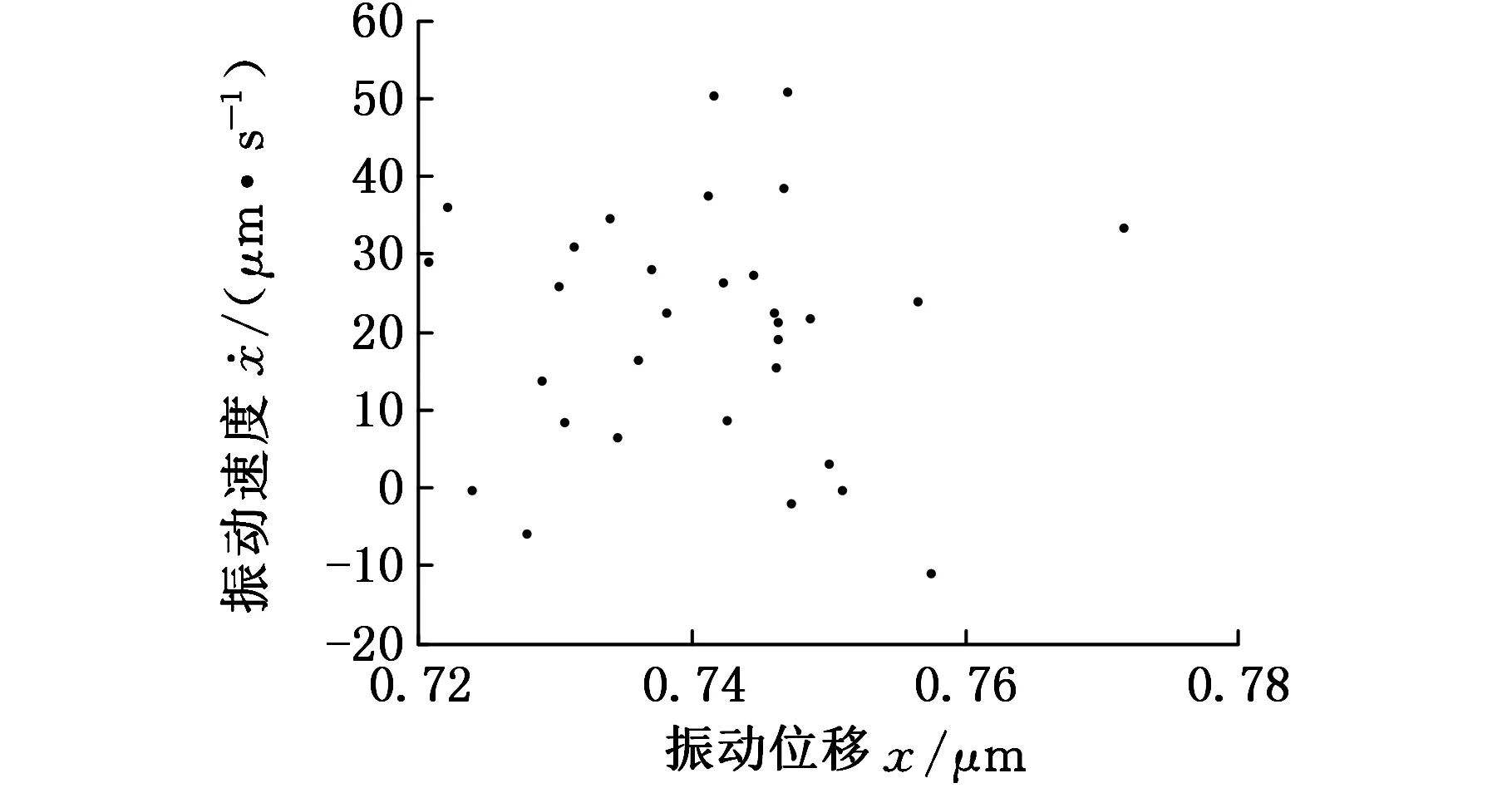
(b)Poincare截面圖7 L1=5 mm時系統的相圖和Poincare截面

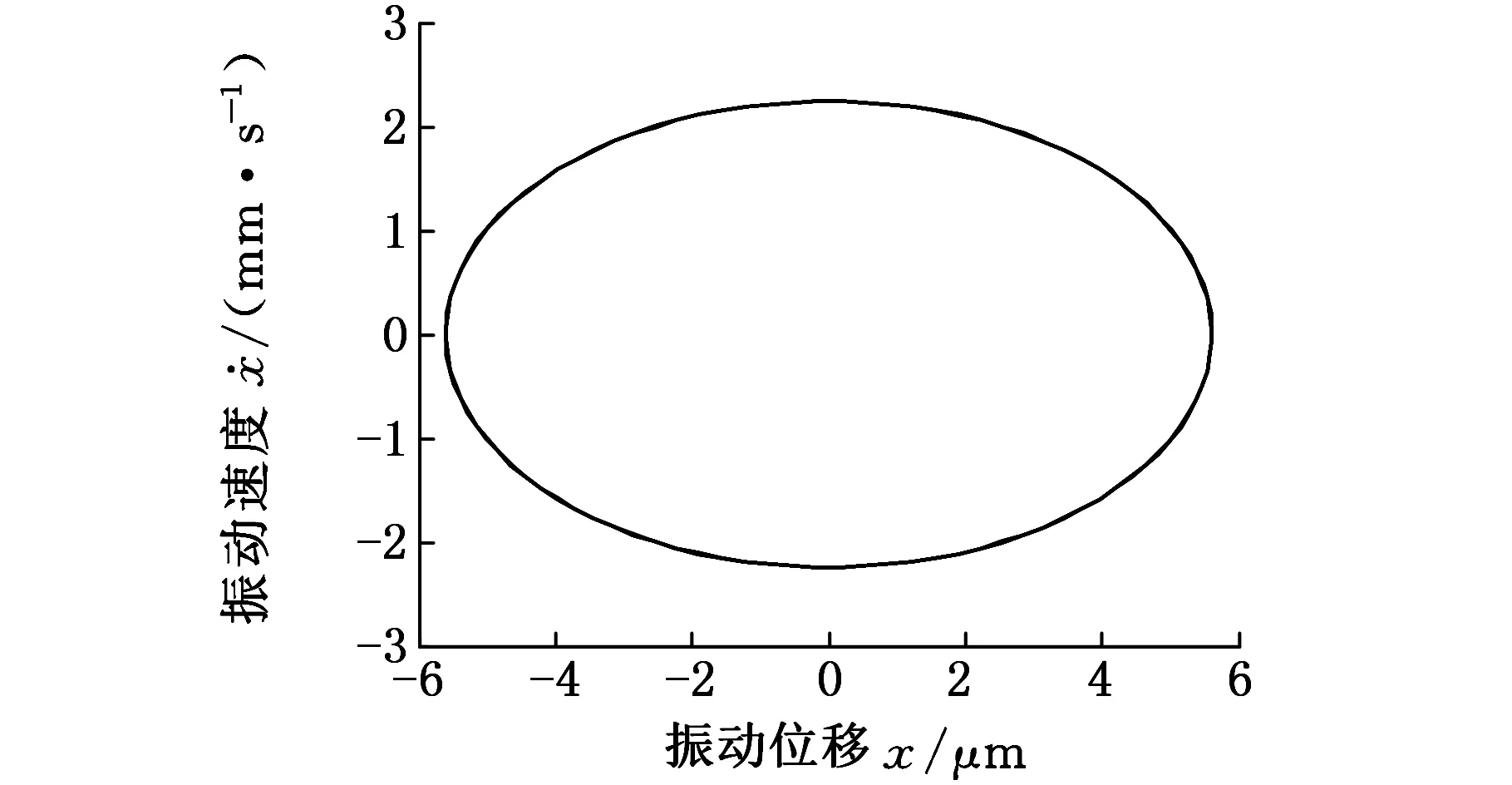
(a)相圖

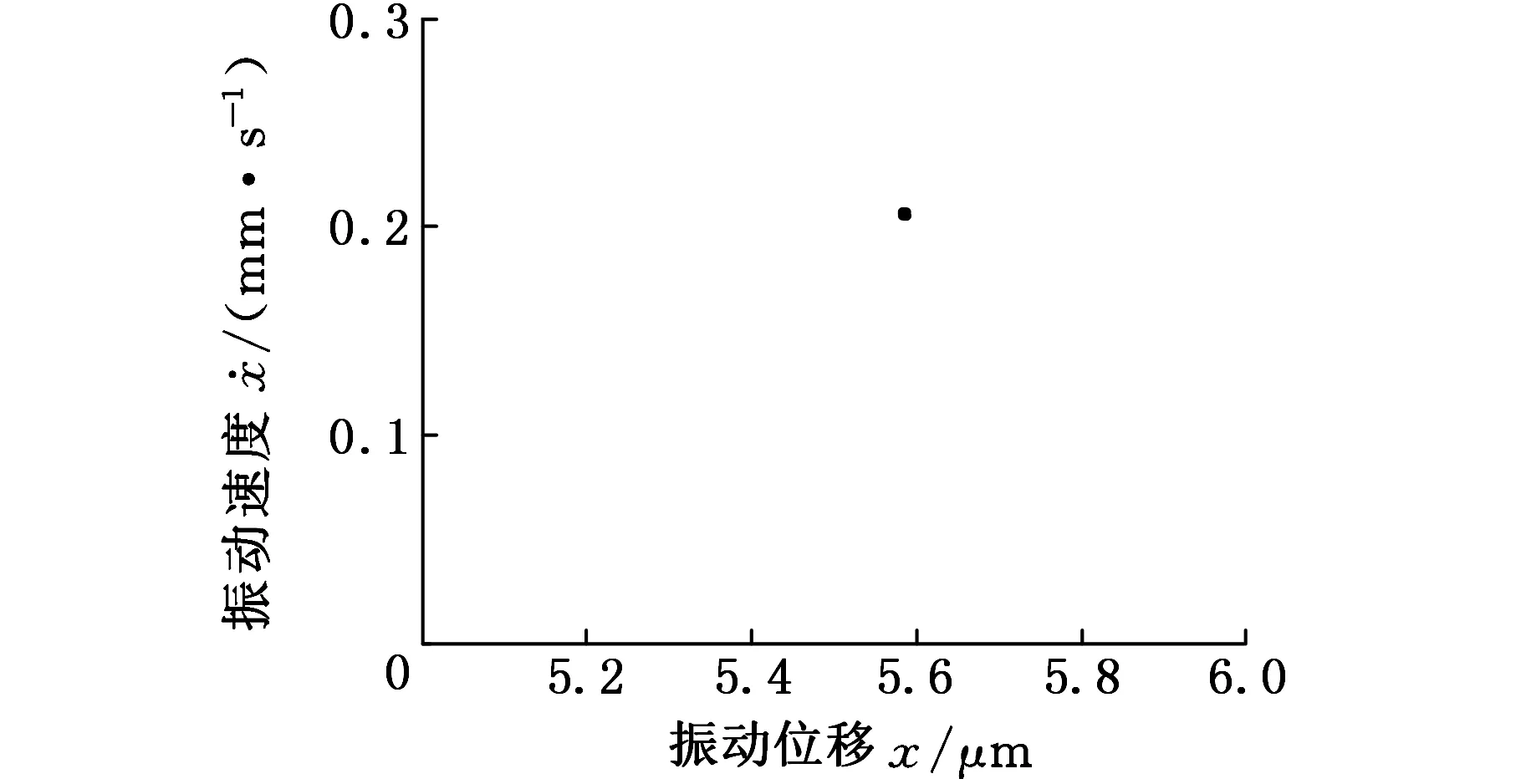
(b)Poincare截面圖8 L1=60 mm時系統的相圖和Poincare截面

(a)相圖

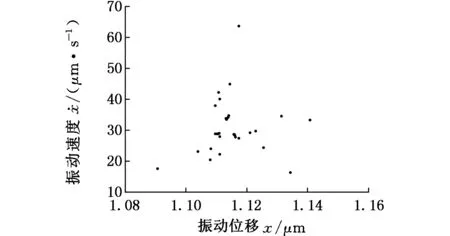
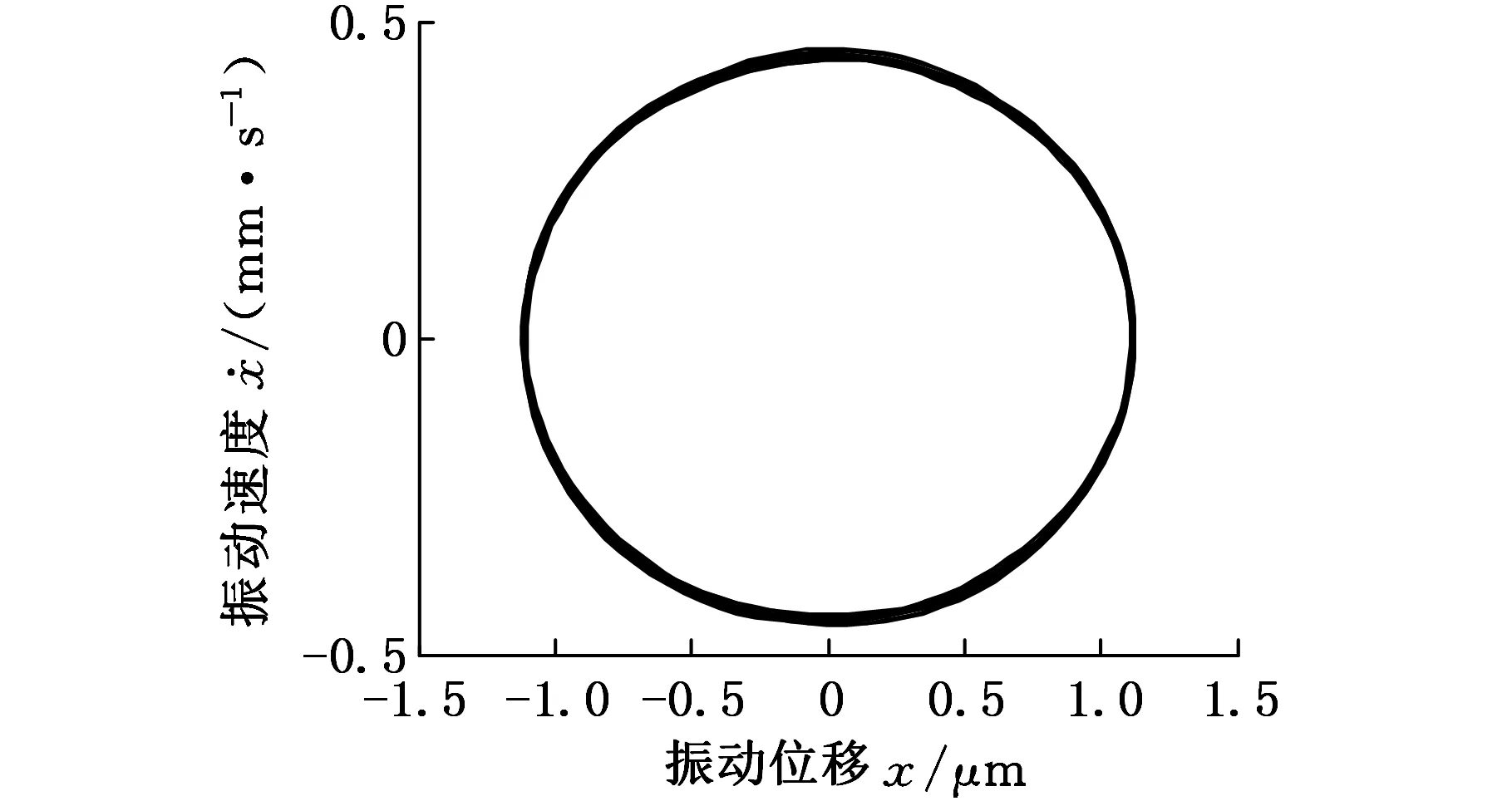
(b)Poincare截面圖9 L1=106 mm時系統的相圖和Poincare截面

由圖6可以看出，液壓缸無桿腔的初始位移位于中間區域時，非線性剛度表現為弱非線性，系統大致上處于周期運動的狀態；液壓缸無桿腔的初始位移位向兩邊靠近時，非線性剛度約束作用較強，分岔行為變得復雜而不穩定。在圖7～圖9中，當L1=60 mm即活塞初始位置處于液壓缸的中間區域時，系統相圖是一封閉的曲線(圖8a)，Poincare截面上表現為一個孤立的點(圖8b)，表明此時系統為周期運動。當L1=5 mm，106 mm即活塞初始位置處于液壓缸的兩端時，系統相圖不再是一個封閉的曲線，其對應的Poincare截面是一些有界離散的點，表明系統已經進入了混沌運動狀態。因此，控制無桿腔的初始位移處于中間區域，能夠有效地保證軋機輥系的穩定性。

圖10～圖13為不同外激勵幅值F時的分岔特性。觀察軋機輥系的分岔響應隨外激勵幅值F的變化規律，并通過相平面圖和Poincare截面對分岔響應加以驗證，分析外激勵幅值對軋機輥系振動的影響。

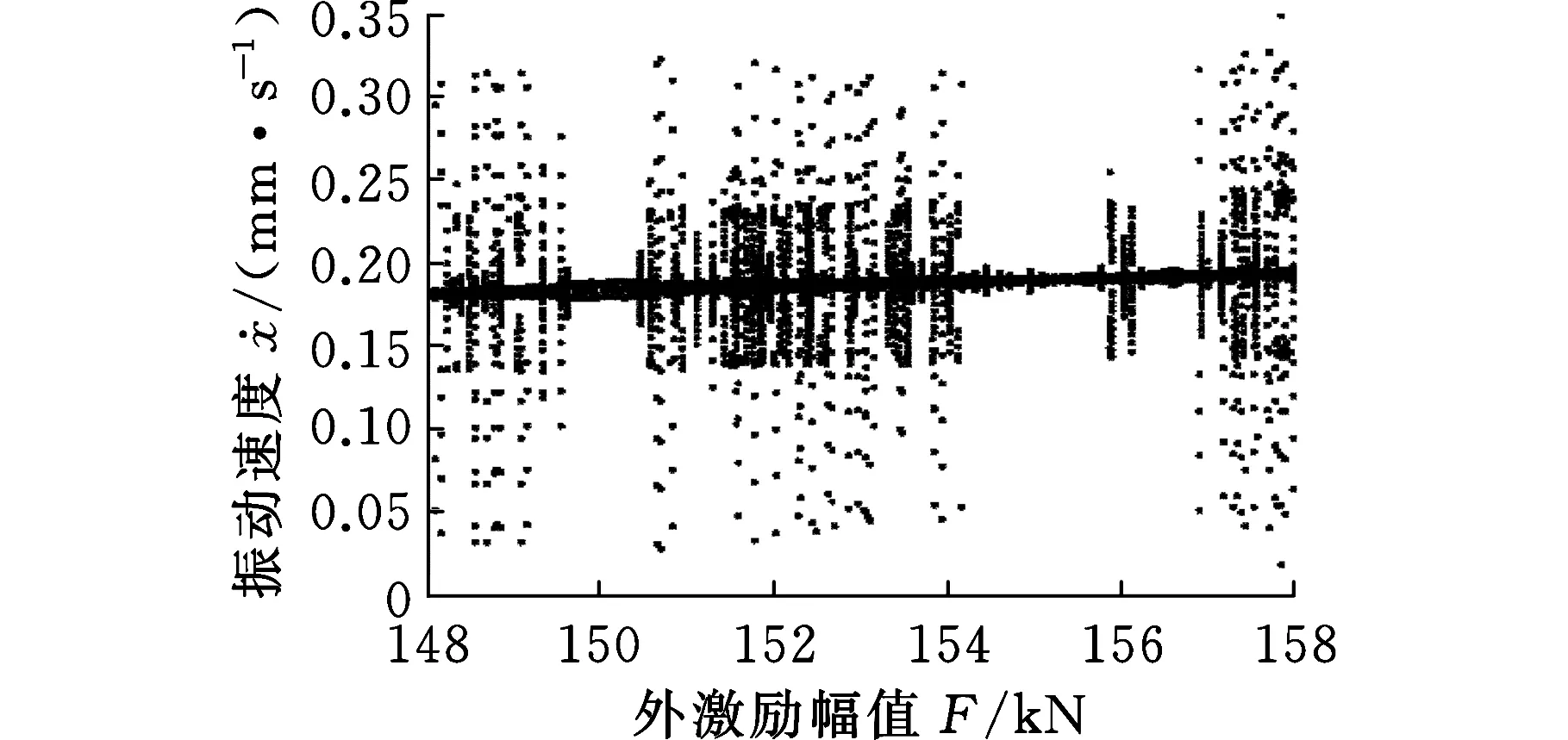
圖10 F變化時的分岔特性

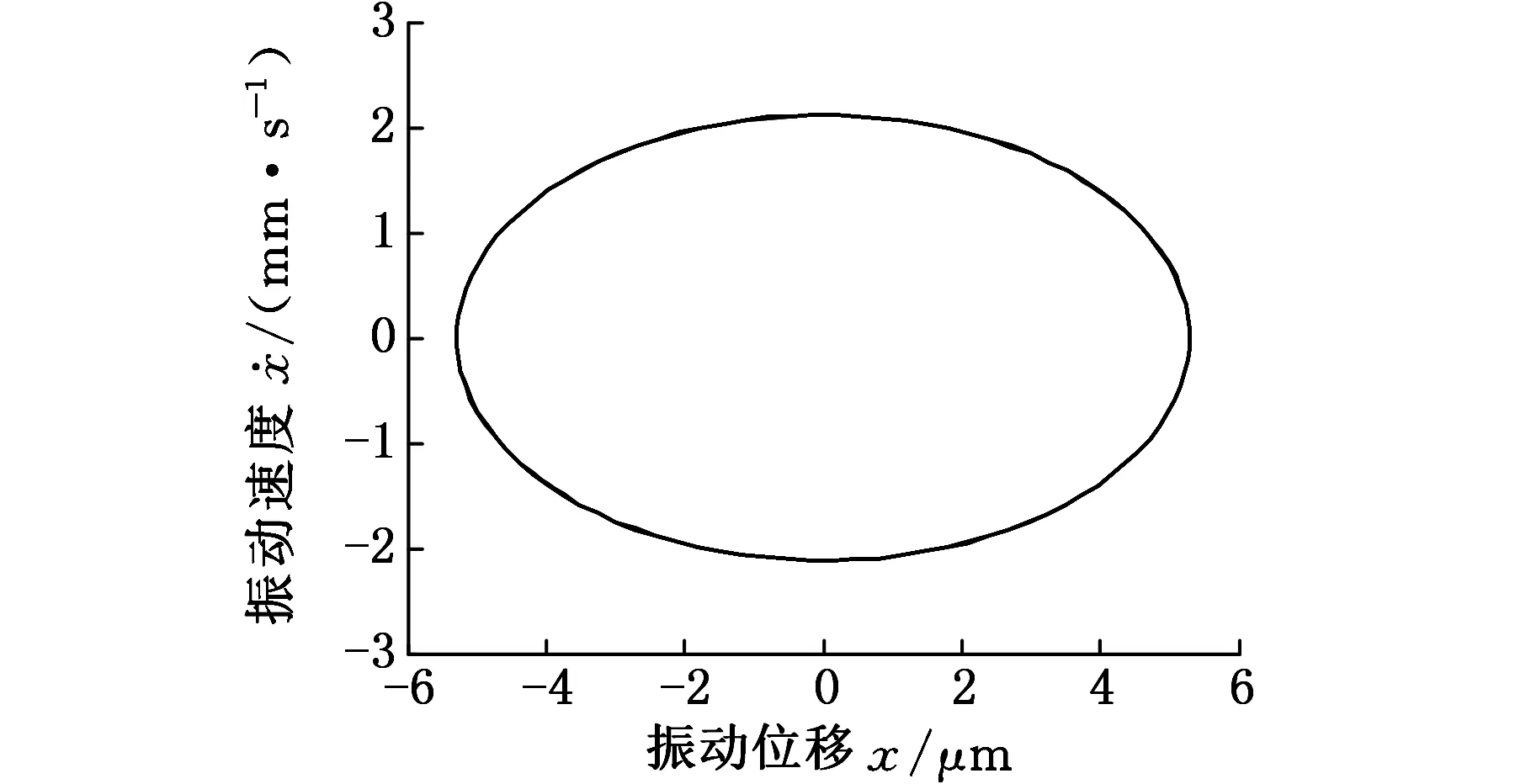
(a)相圖

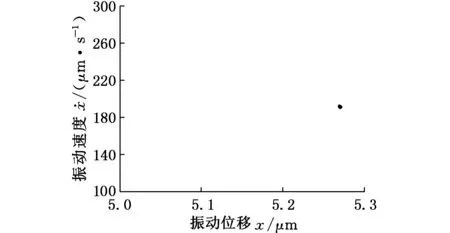
(b)Poincare截面圖11 F=156 kN時系統的相圖和Poincare截面

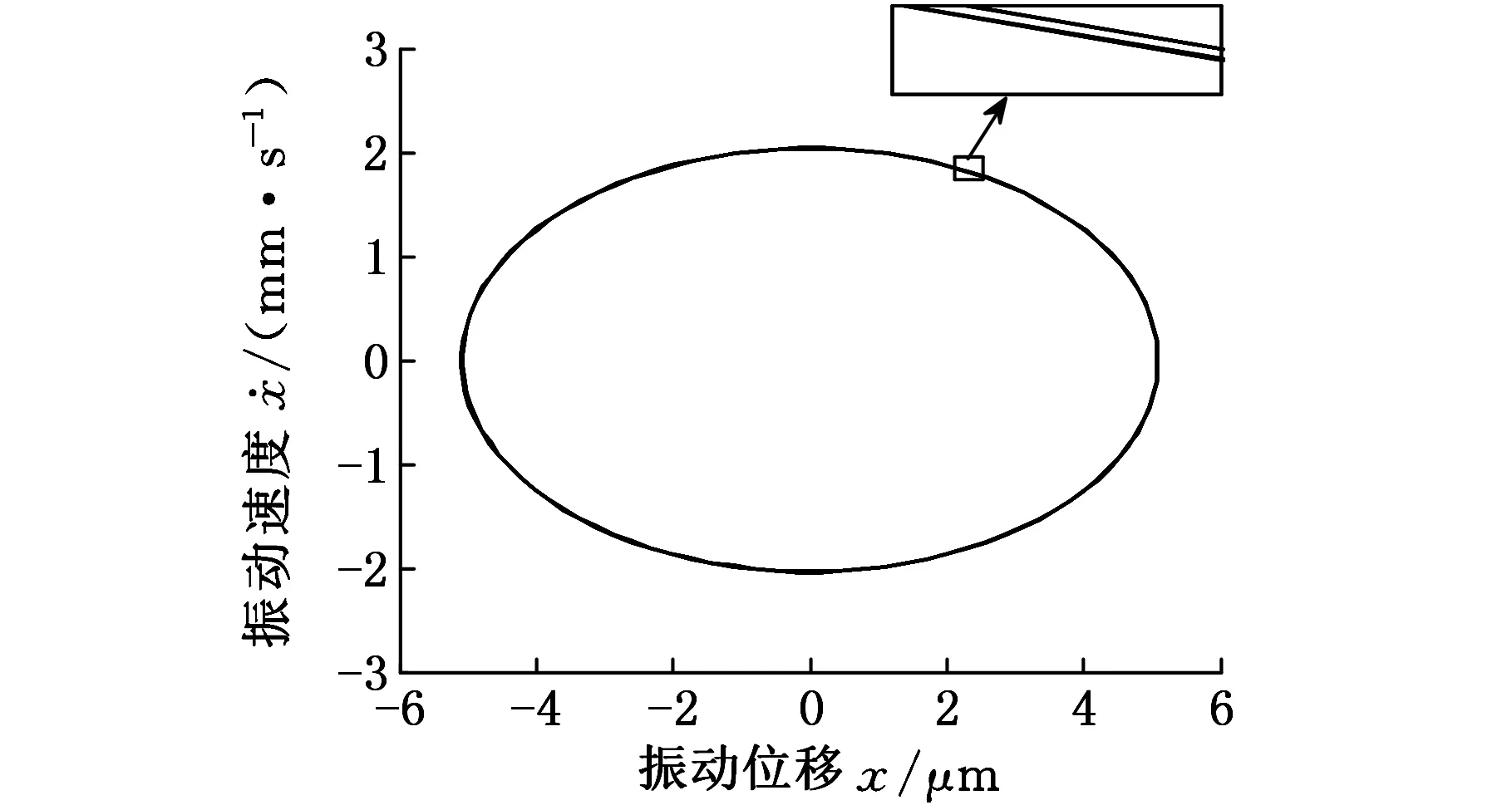
(a)相圖

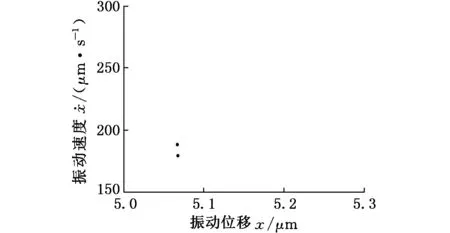
(b)Poincare截面圖12 F=150 kN時系統的相圖和Poincare截面

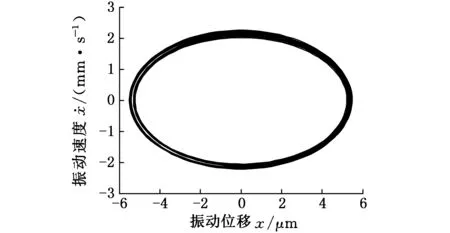
(a)相圖

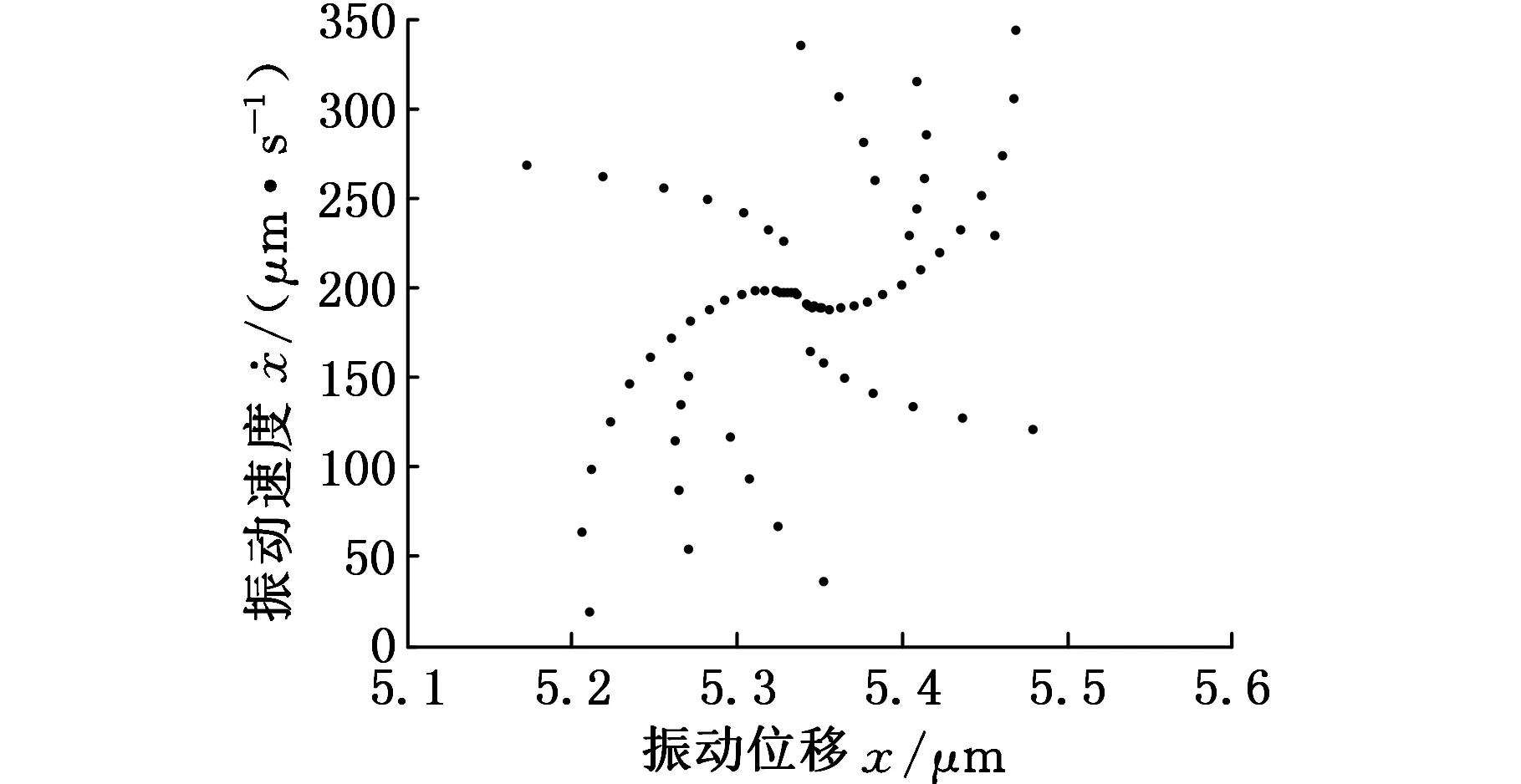
(b)Poincare截面圖13 F=158 kN時系統的相圖和Poincare截面

從圖10中可以發現，隨著外激勵幅值的變化，軋機輥系振動在周期運動、倍周期運動和混沌運動等多種運動狀態之間交替變化。當F=156 kN時(圖11)，系統相圖是一個封閉的曲線，Poincare截面上表現為一個孤立的點，表明此時系統為周期運動。當F=150 kN時(圖12)，系統相圖仍是一個封閉的曲線，Poincare截面上表現為兩個孤立的點，說明軋機輥系將會出現倍周期運動。當F=158 kN時(圖13)，系統相圖不再是一個封閉的曲線，其對應的Poincare截面是一些有界離散的點，表明系統已經進入了混沌運動狀態。

結合圖6～圖13所示的分岔圖、平面圖和Poincare截面可以發現，無桿腔初始位移和外激勵幅值的變化影響著軋機系統的動力學行為，軋機輥系可能出現周期運動、倍周期運動和混沌運動等復雜的運動狀態，使軋制產品表面出現有規律的周期振紋或振痕，影響軋制產品的質量。

5.3 反饋控制研究

考慮到軋機振動的不可預測性，對此系統加入控制輸入，基于Lyapunov判別法，給出系統漸進穩定的條件，通過數值仿真，對比分析加入控制前后的系統的穩定性。

圖14～圖17為加入控制前后的時域曲線和相平面曲線。圖14和圖15所示分別為振動位移曲線和振動速度曲線，為了清晰地表現加入控制后的效果，在t≥0.05 s時才加入控制。從圖14和圖15可以看出，加入控制前，系統的運動是混亂無序的；加入控制后，經過短暫的時間，系統的運動曲線開始進行等幅振蕩并且幅值有很大程度的減小。圖16為t≥0時的相平面曲線，圖17為t≥0.05 s的相平面曲線，對比圖16和圖17可以發現，系統在沒加入控制之前，系統的運動是非常復雜的，加入控制后系統開始進入穩定的周期運動。由圖14～圖17可以看出，控制輸入量的加入對軋機輥系振動行為有著較為明顯的作用。反饋控制的加入可減少軋機輥系劇烈振動現象的發生，保證系統的穩定運行。

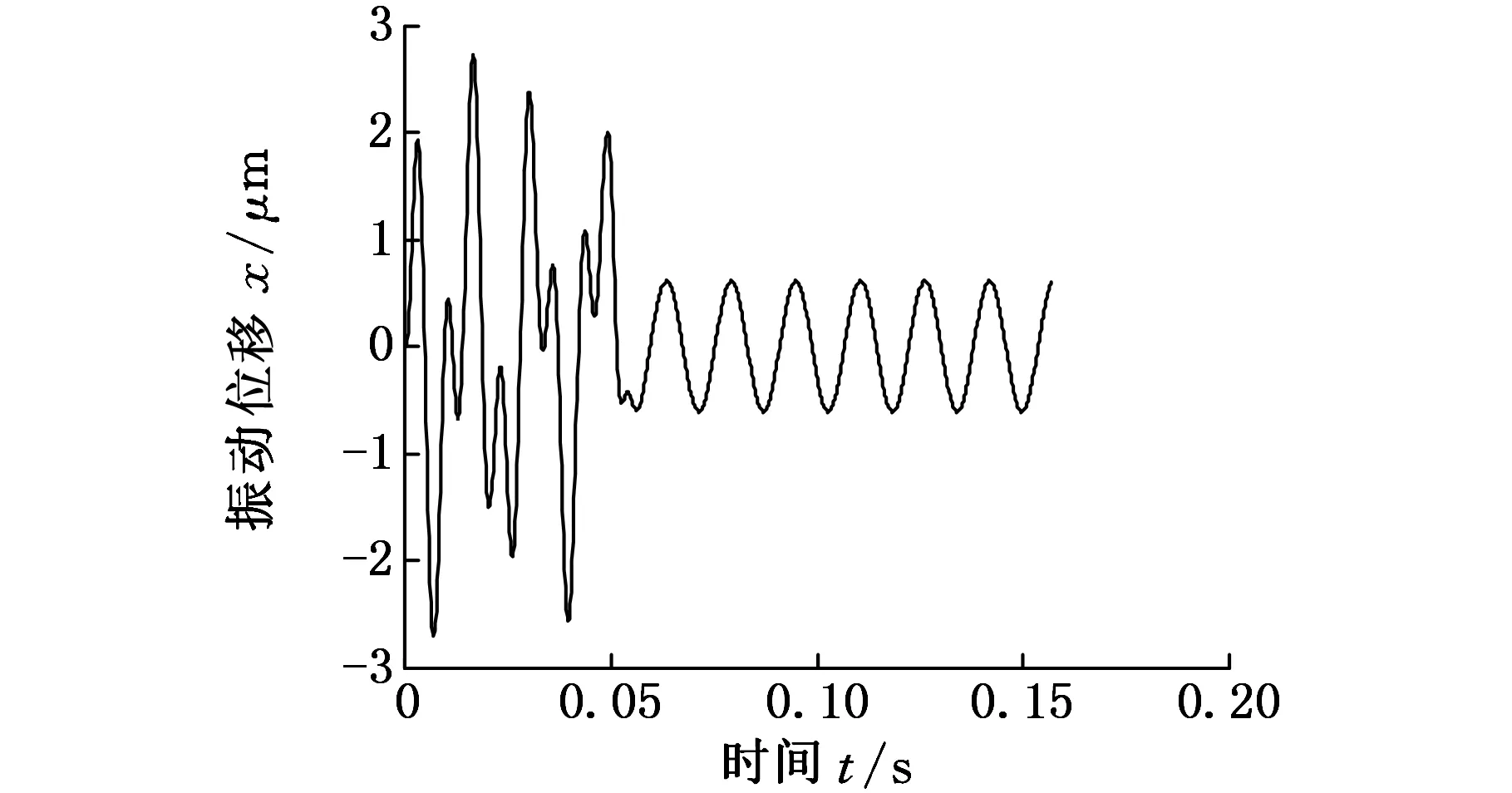
圖14 位移曲線

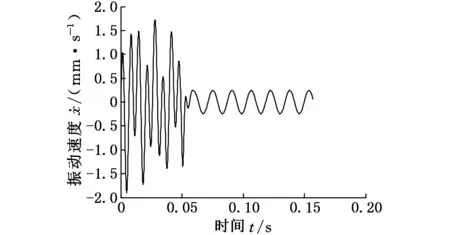
圖15 速度曲線

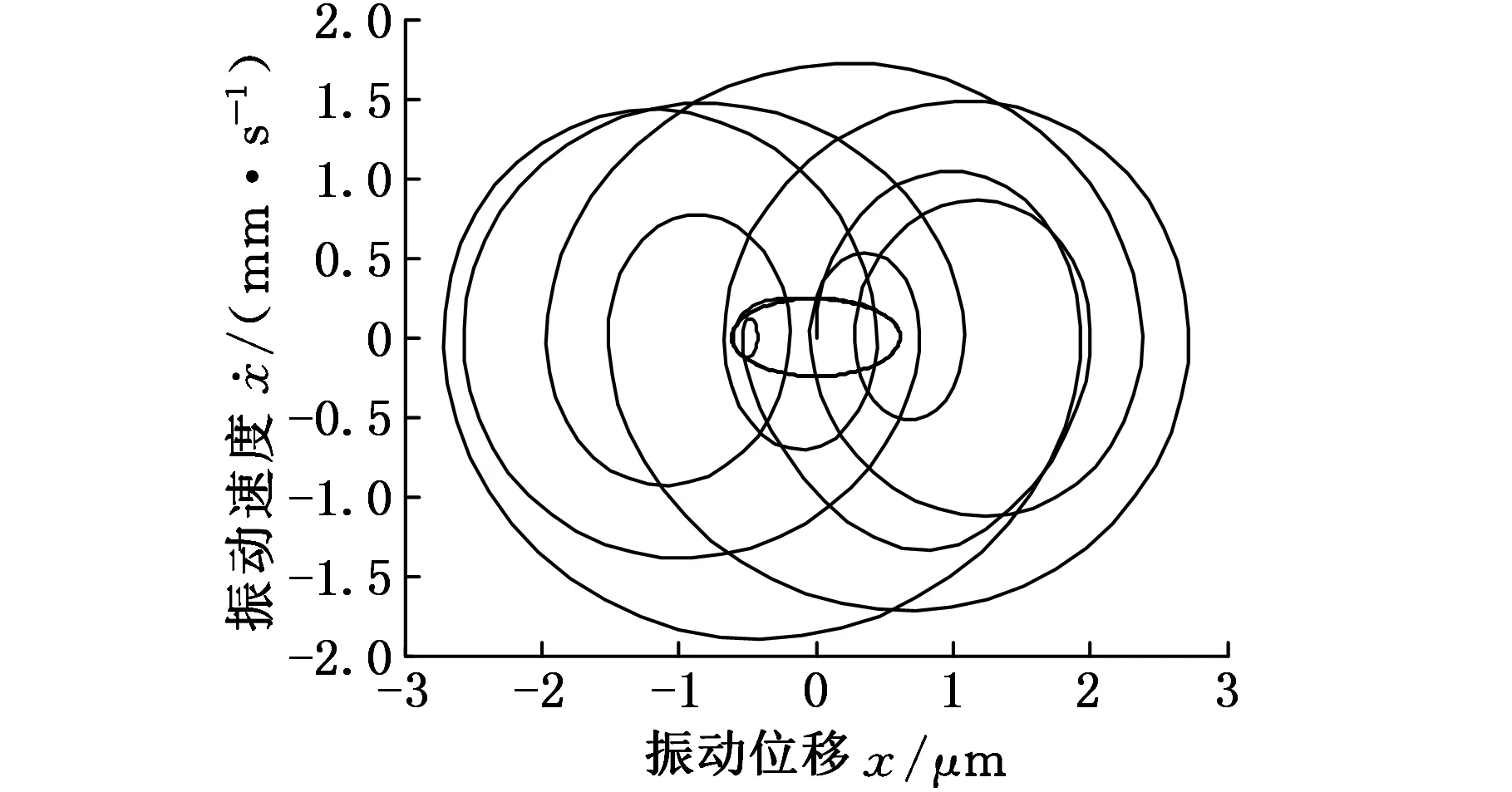
圖16 相平面曲線

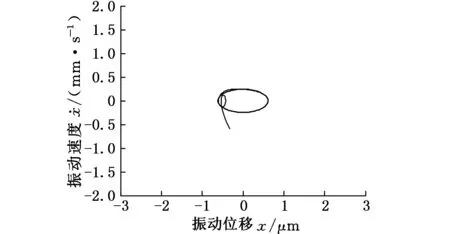
圖17 t≥0.05 s時的相平面曲線

6 結論

(1)考慮軋制過程中液壓系統動態特性的影響，建立了一種液壓缸非線性剛度約束下的軋機振動模型。在該模型基礎上，求得幅頻響應方程，并仿真分析非線性剛度系數、外激勵幅值和無桿腔初始位移等參數對軋機振動的影響。

(2)分析了外激勵幅值和無桿腔初始位移對軋機系統分岔特性的影響，發現在不同的外激勵幅值和無桿腔初始位移下，軋機輥系振動在周期運動、倍周期運動和混沌運動等多種運動狀態之間交替變化。因此，可以通過調節外激勵幅值和無桿腔初始位移等參數改變軋機輥系的動力學行為。

(3)對比加入控制前與控制后的系統時域曲線和相平面曲線，發現系統在沒加入控制之前，系統的運動是混亂無序的，加入控制后系統經過短暫的時間開始穩定地周期運動，表明了反饋控制器的有效性。這為保證軋機輥系的平穩運行提供了理論參考。

[1] Wu Shengli, Shao Yimin, Wang Liming, et al. Relationship between Vibration Marks and Rolling Force Fluctuation for Twenty-high Roll Mill[J]. Engineering Failure Analysis, 2015, 55(1): 87-99.

[2] Heidari A, Forouzan M R.Optimization of Cold Rolling Process Parameters in Order to Increasing Rolling Speed Limited by Chatter Vibrations[J]. Journal of Advanced Research,2013,4(1):27-34.

[3] Bar A,Swiatoniowski A. Interdependence between the Rolling Speed and Non-linear Vibrations of the Mill System[J]. Journal of Materials Processing Technology, 2004, 155/156: 2116-2121.

[4] 楊旭，李擎，童朝南，等. 基于輥縫動態摩擦方程的鋁板冷軋機垂振機理分析[J]. 北京科技大學學報, 2014, 36(1): 104-109. Yang Xu, Li Qing, Tong Chaonan, et al. Vertical Vibration Mechanism Analysis of Aluminum Cold Rolling Mills Based on the Dynamic Friction Equation In Roll Gap[J]. Journal of University of Science and Technology Beijing, 2014, 36(1): 104-109.

[5] 范小彬，臧勇，王會剛. 熱連軋機水平振動特性研究[J]. 鋼鐵, 2010, 45(9): 62-66. Fan Xiaobin, Zang Yong, Wang Huigang. Research on Hot Rolling Mill Horizontal Vibration[J]. Iron and Steel, 2010, 45(9): 62-66.[6] 劉浩然，劉飛，侯東曉，等. 多非線性彈性約束下軋機輥系振動特性[J]. 機械工程學報,2012,48(9):89-94. Liu Haoran, Liu Fei, Hou Dongxiao, et al. Vibration Characteristics of Mill Rolls under Multi-segment Nonlinear Elastic Constraints[J]. Journal of Mechanical Engineering, 2012, 48(9): 89-94.

[7] Tran X B, Hafizah N, Yanada H. Modeling of Dynamic Friction Behaviors of Hydraulic Cylinders[J]. Mechatronics, 2012, 22(1) 65-75.

[8] 王林鴻，吳波，杜潤生，等. 液壓缸運動的非線性動態特征[J]. 機械工程學報，2007, 43(12): 12-19. Wang Linhong, Wu Bo, Du Runsheng, et al. Nonlinear Dynamic Characteristics of Moving Hydraulic Cylinder[J]. Journal of Mechanical Engineering, 2007, 43(12): 12-19.

[9] 朱勇，姜萬錄，劉思遠，等. 非線性液壓彈簧力對電液伺服系統非線性動力學行為影響的研究[J]. 中國機械工程, 2015, 26(8): 1085-1091. Zhu Yong, Jiang Wanlu, Liu Siyuan, et al. Research on Influences of Nonlinear Hydraulic Spring Force on Nonlinear Dynamic Behaviors of Electro-hydraulic Servo System[J]. China Mechanical Engineering, 2015, 26(8): 1085-1091.

[10] Lorinc M, Szabolcs F, Nariman S. A Practical Method for Friction Identification in Hydraulic Actuators[J]. Mechatronics, 2011, 21(1): 350-356.

[11] Hu P H, Ehmann K F. A Dynamic Model of the Rolling Process. Part 1: Homogeneous Model; Part 2: Inhomogeneous Model[J]. International Journal of Machine Tools and Manufacture, 2000, 40(1): 1-31.

[12] Nijmeijer H, Berghuis H. On Lyapunov Control of the Duffing Equation[J]. IEEE Transactions on Circuits and Systems I,1998,42 (8):473-477.

(編輯 蘇衛國)

Vibration Behavior and Control of Roll System under Nonlinear Stiffness of a Hydraulic Cylinder

Liu Bin Li Peng Liu Fei Liu Haoran Jiang Jiahao

Yanshan University,Qinhuangdao,Hebei,066004

For the vibrations of rolling mill under the influences of dynamic characteristics of hydraulic system, a kind of vibration model of a roll system was established under the constraints of the nonlinear stiffness of hydraulic cylinder. Amplitude-frequency response of the vibration system was obtained by using average method, the feedback controller of the system was designed based on the Lyapunov second method. Lastly, parameters of the actual mill were used to conduct a simulation research and parameters such as nonlinear stiffness coefficient, external excitation and initial displacement of the rodless cavity were analyzed how did which to affect the amplitude-frequency response. The dynamic bifurcation characteristics of the excitation amplitude and the initial displacement of the rodless cavity were studied, results show that as the changes of the parameters, the rolling mill will cause periodic, period-doubling, chaotic motion and a series of complex movements. At the same time, the feedback control was introduced, and the effectiveness of the feedback controller was verified by comparing the time domain curves and the phase plane curves, which provides a theoretical basis to improve the stability of rolling mill rolls.

rolling mill vibration; amplitude-frequency response; feedback controller; bifurcation characteristics

2015-12-18

國家自然科學基金資助項目(51405068)；河北省自然科學基金資助項目(E2015203349)

TH113；O322

10.3969/j.issn.1004-132X.2016.23.012

劉 彬，男，1953年生。燕山大學電氣工程學院教授、博士研究生導師。主要研究方向為軋機振動及測量技術。李 鵬，男，1990年生。燕山大學電氣工程學院碩士研究生。劉 飛，男，1986年生。燕山大學信息科學與工程學院博士研究生。劉浩然，男，1980年生。燕山大學信息科學與工程學院副教授。姜甲浩，男，1991年生。燕山大學電氣工程學院碩士研究生。