基于Hopf振蕩器的六足機器人步態(tài)CPG模型設(shè)計

任杰，徐海東，干蘇，王斌銳

(中國計量學(xué)院 機電工程學(xué)院，浙江 杭州 310018)

?

基于Hopf振蕩器的六足機器人步態(tài)CPG模型設(shè)計

任杰，徐海東，干蘇，王斌銳

(中國計量學(xué)院 機電工程學(xué)院，浙江 杭州 310018)

利用中樞模式發(fā)生器實現(xiàn)六足機器人爬行步態(tài)是運動仿生的關(guān)鍵。建立機器人坐標(biāo)系，基于D-H參數(shù)求解正運動學(xué)；采用Hopf振蕩器設(shè)計多腿耦合模型；構(gòu)建由6個CPG單元組成的環(huán)形CPG網(wǎng)絡(luò)拓撲結(jié)構(gòu)，每個CPG單元由2個耦合的Hopf振蕩器組成，分別輸出髖關(guān)節(jié)、踝關(guān)節(jié)運動信號；采用膝踝映射函數(shù)方法，將踝關(guān)節(jié)輸出信號映射為踝關(guān)節(jié)和膝關(guān)節(jié)角度軌跡，從而降低網(wǎng)絡(luò)中振蕩器個數(shù)；通過改變耦合系數(shù)保證相鄰振蕩器的相位互鎖，輸出穩(wěn)定平滑信號；搭建實物樣機進行步態(tài)測試。仿真和實驗表明，CPG網(wǎng)絡(luò)相位差穩(wěn)定，可實現(xiàn)六足機器人三角步態(tài)下的平穩(wěn)行走，爬行速度約為6.45 cm/s。

中樞模式發(fā)生器；Hopf振蕩器；六足機器人；運動學(xué)分析

六足機器人具有穩(wěn)定的機械結(jié)構(gòu)、靈活多變的行走方式，適合在復(fù)雜環(huán)境下工作，被廣泛應(yīng)用于災(zāi)后探測、環(huán)境勘測等工作中。大量研究表明，昆蟲及其他生物的節(jié)律步態(tài)，是根據(jù)生物神經(jīng)節(jié)律控制機理產(chǎn)生的一種自激振蕩、相位互鎖的運動模式，由位于生物低級神經(jīng)中樞的中樞模式發(fā)生器(central pattern generator,CPG)產(chǎn)生的信號控制[1-2]。CPG已被廣泛應(yīng)用于機器魚、機器海龜、機器果蠅等機器人控制領(lǐng)域[3-5]。與傳統(tǒng)的基于模型的機器人控制方法相比，CPG不需要對機器人本體和環(huán)境進行建模，不依賴于外部反饋和高層命令而產(chǎn)生穩(wěn)定的節(jié)律運動，可適應(yīng)非結(jié)構(gòu)化環(huán)境，具有運動模式多樣、耦合性強、自適應(yīng)性強等優(yōu)點。

根據(jù)不同的應(yīng)用環(huán)境，CPG模型被分為不同類型[2]，如生物神經(jīng)元模型、半中心模型、耦合振蕩器模型等。常見的主要是半中心模型和耦合振蕩器模型。半中心模型是模擬伸肌和屈肌的交替運動。根據(jù)半中心模型思想，Matsuoka對漏極積分器進行改進，加入模擬神經(jīng)元適應(yīng)特性的疲勞項，構(gòu)成Matsuoka神經(jīng)振蕩器[3]。基于Matsuoka振蕩器模型，Kimura等[4]在CPG中加入傳感器反饋，采用2個相互抑制的屈肌和伸肌神經(jīng)元構(gòu)成了Kimura模型，提高了四足機器人運動的穩(wěn)定性，但存在控制算法復(fù)雜，參數(shù)難調(diào)節(jié)等缺點。耦合振蕩器模型由非線性振蕩器組成，模型參數(shù)直接對應(yīng)輸出曲線的物理含義，實現(xiàn)幅值、頻率等參數(shù)可調(diào)，便于控制。常見的有Kuramoto振蕩器模型、Hopf振蕩器模型、Wilson-Cowan振蕩器模型等[6-7]。A. J. Ijspeert團隊[8]將非線性振蕩器應(yīng)用在兩棲蠑螈機器人上，實現(xiàn)了機器人游泳和步行運動。

本文仿生對象是螞蟻。首先參考螞蟻的腿部結(jié)構(gòu)比例，進行單腿正運動學(xué)分析，設(shè)計六足機器人。其次，采用L. Righetti和A. J. Ijspeert的改進Hopf非線性振蕩器構(gòu)建CPG模型[9]，構(gòu)建環(huán)形網(wǎng)絡(luò)拓撲結(jié)構(gòu)。然后設(shè)計膝踝映射函數(shù)，減少振蕩器數(shù)量，優(yōu)化了CPG網(wǎng)絡(luò)結(jié)構(gòu)；通過Matlab仿真得到關(guān)節(jié)角度；最后在六足機器人上進行實物驗證。

1 六足機器人的基本機構(gòu)及步態(tài)

1.1 六足機器人機構(gòu)

本文設(shè)計的六足仿生機器人分為軀干和肢體兩部分，仿生對象為螞蟻。肢體設(shè)計參考了非洲紅火蟻的腿部結(jié)構(gòu)比例，如圖1所示，螞蟻的腿部主要由基節(jié)、股節(jié)、脛節(jié)及跗節(jié)等組成。通過觀察發(fā)現(xiàn)，螞蟻的腿部自由度較多。為簡化設(shè)計，六足機器人每條腿3個自由度，分別為髖關(guān)節(jié)、膝關(guān)節(jié)和踝關(guān)節(jié)，對應(yīng)螞蟻腿部分別是基關(guān)節(jié)、基-股關(guān)節(jié)、股-脛關(guān)節(jié)。其中，機器人的膝關(guān)節(jié)和踝關(guān)節(jié)轉(zhuǎn)軸與地面平行，髖關(guān)節(jié)轉(zhuǎn)軸與另外2個關(guān)節(jié)垂直，髖關(guān)節(jié)控制單腿的水平方向的橫擺。

根據(jù)仿生螞蟻腿部結(jié)構(gòu)及機器人學(xué)原理，對六足機器人進行運動學(xué)建模。圖2為六足機器人機構(gòu)坐標(biāo)系，圖2(a)中c為機器人軀干質(zhì)心坐標(biāo)原點，定義∑c表示機器人軀干質(zhì)心坐標(biāo)系，zc沿垂直身體向上，xc沿身體橫向方向，yc坐標(biāo)軸通過右手螺旋定則確定，為軀體軸線前進方向。omi為m腿i關(guān)節(jié)中心坐標(biāo)原點，用∑omi表示其關(guān)節(jié)坐標(biāo)系，∑om0表示機器人腿部基坐標(biāo)系。圖2(b)中，m=1,2，…，6為機器人腿序號，i=1,2,3為腿部關(guān)節(jié)序號，分別表示髖關(guān)節(jié)、膝關(guān)節(jié)和踝關(guān)節(jié)，i=4時表示機器人足端，zmi為沿關(guān)節(jié)旋轉(zhuǎn)方向坐標(biāo)軸，xmi為沿連桿軸線方向坐標(biāo)軸。L1、L2、L3分別為基節(jié)、股節(jié)、脛節(jié)長度。

(a)螞蟻腿部

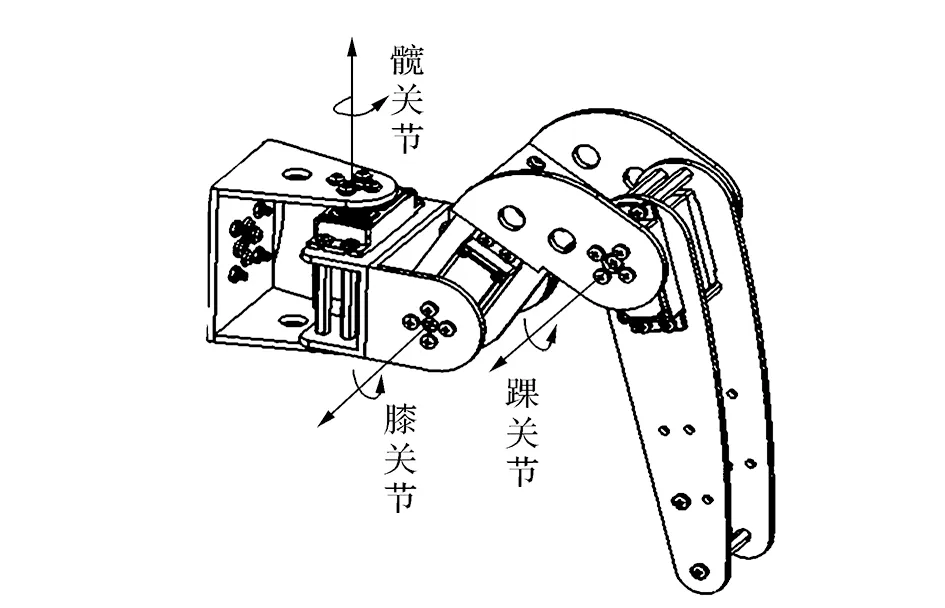
(b)樣機腿部

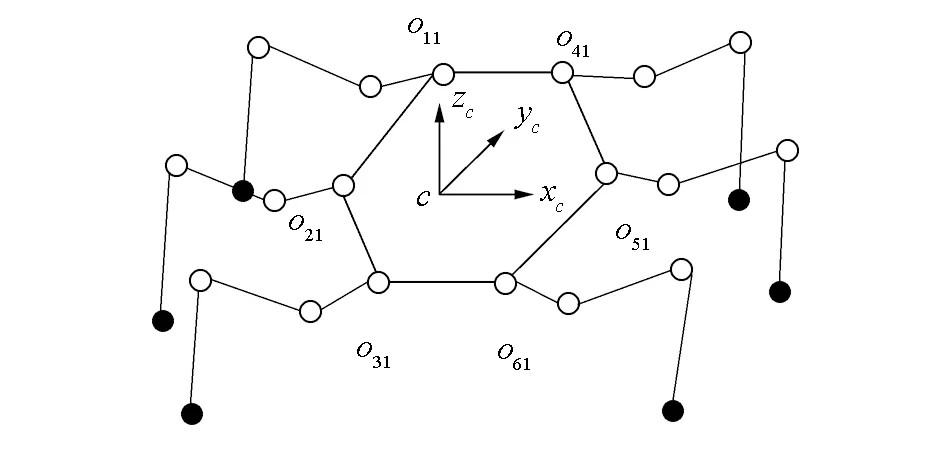
(a)軀干坐標(biāo)系

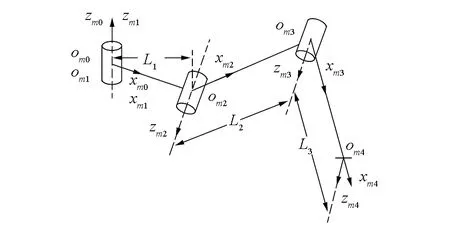
(b)單腿關(guān)節(jié)坐標(biāo)系

1.2 正運動學(xué)分析

根據(jù)齊次坐標(biāo)變換原理，通過齊次變換，可將機器人腿部基準(zhǔn)坐標(biāo)系∑om0變換到軀干質(zhì)心坐標(biāo)系∑c中，變換矩陣cTomo為

式中：(xom0,yom0,zom0)為機器人腿部基坐標(biāo)系到軀干質(zhì)心坐標(biāo)系的平移坐標(biāo)值，φ為腿部基坐標(biāo)系∑om0到軀干質(zhì)心坐標(biāo)系∑c變換繞z軸的旋轉(zhuǎn)角度。將表1中參數(shù)帶入式(1)中，可以求得機器人腿部基坐標(biāo)系與軀干質(zhì)心坐標(biāo)系之間的關(guān)系。

表1 基坐標(biāo)系到軀干質(zhì)心坐標(biāo)系變換參數(shù)

Table 1 Transformation parameters of base coordinates to geocentric coordinate system

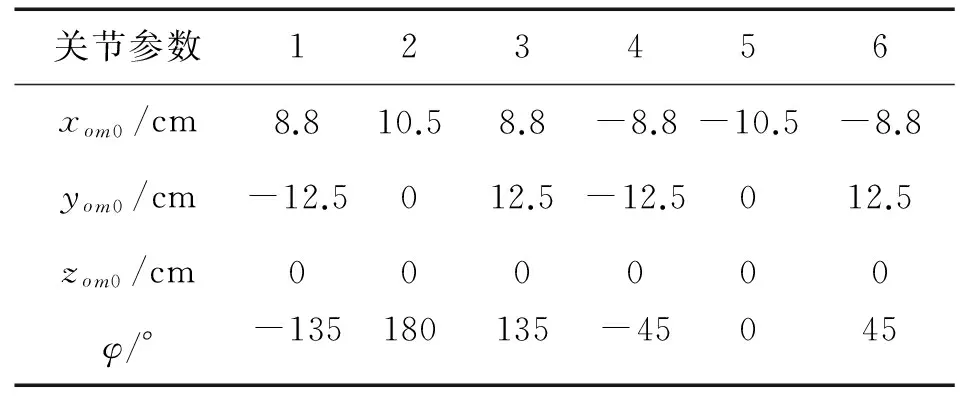
關(guān)節(jié)參數(shù)123456xom0/cm8.810.58.8-8.8-10.5-8.8yom0/cm-12.5012.5-12.5012.5zom0/cm000000φ/°-135180135-45045

機器人右側(cè)腿部機構(gòu)D-H參數(shù)如表2所示，θi表示第i個關(guān)節(jié)的轉(zhuǎn)動角度。左側(cè)腿D-H參數(shù)，除1=-π2，其他參數(shù)與右側(cè)腿一致，均保持不變。

表2 右側(cè)腿部機構(gòu)D-H參數(shù)表

根據(jù)D-H坐標(biāo)變換法[10]，機器人足端點坐標(biāo)系∑om4在軀干質(zhì)心坐標(biāo)系∑c中的位姿為

可求得右側(cè)腿的運動學(xué)正解為

左側(cè)腿的運動學(xué)正解為

1.3 六足機器人三角步態(tài)描述

步態(tài)指機器人的每條腿按一定順序和軌跡的運動形式，包括通過調(diào)整邁步順序和頻率來調(diào)整身體的位姿[11]。

步態(tài)周期T為機器人完成一次完整步態(tài)所需要的時間。機器人單腿的邁步幅度稱為步長。占空比為單腿在一個步態(tài)周期內(nèi)，處于支撐相的時間在整個步態(tài)周期中所占比例，用字母γ表示。

六足機器人步態(tài)通常按照與地面接觸腳的數(shù)目來劃分。常見有三角步態(tài)、跟導(dǎo)步態(tài)和波動步態(tài)。三角步態(tài)是昆蟲穩(wěn)定行走時速度最快的一種步態(tài)。圖3為一個步行周期內(nèi)六足機器人的三角步態(tài)支撐相與擺動相示意圖。白色表示擺動相，黑色陰影表示支撐相，腿1、腿3、腿5為一組，腿2、腿4、腿6為一組，同組腿相位相同，異組腿相位相差π。機器人行走時占空比分為3種情形：1)γ=0.5，即每條腿的支撐與擺動時間相等，一組腿支撐，另一組腿擺動(見圖3(a))；2)γ>0.5，即每條腿支撐時間大于擺動時間，6條腿出現(xiàn)同時著地的情況(見圖3(b))，此種情況下，機器人穩(wěn)定性較高，但速度較慢；3)γ<0.5，即每條腿支撐時間小于擺動相時間，6條腿出現(xiàn)同時懸空狀況(見圖3(c))，顯然，這一情況機器人速度快但穩(wěn)定性欠佳。占空比對爬行速度有直接影響。本文選擇占空比為0.5的三角步態(tài)作為研究對象。

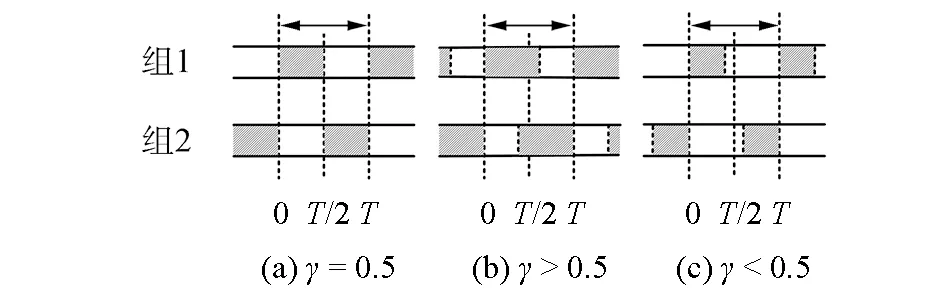
圖3 六足機器人三角步態(tài)支撐相與擺動相示意圖

2 CPG振蕩器網(wǎng)絡(luò)模型與仿真

2.1 CPG振蕩器模型

中樞模式發(fā)生器(central pattern generator, CPG)是一種離散神經(jīng)網(wǎng)絡(luò)，能夠產(chǎn)生復(fù)雜的高維信號控制動物的節(jié)律運動[12]。機器人學(xué)上，CPG通常被看作耦合動態(tài)系統(tǒng)，即非線性振蕩器模型。CPG神經(jīng)元的自發(fā)振動性與傳統(tǒng)的機械振動類似，是通過采用互相連接的單個或者多個非線性振蕩器來模擬CPG產(chǎn)生信號。其中非線性振蕩器都有極限環(huán)，若極限環(huán)穩(wěn)定，系統(tǒng)中所有的軌跡都會接近該極限環(huán)，這樣即使系統(tǒng)中有小的擾動，系統(tǒng)也能回到穩(wěn)定狀態(tài)。

Hopf振蕩器存在一個穩(wěn)定的極限環(huán)，鄰域中的軌線都螺旋趨近該極限環(huán)，具有很好的穩(wěn)定性。與傳統(tǒng)Hopf振蕩器相比，本文采用改進的Hopf振蕩器作為機器人信號發(fā)生器，不僅可以實現(xiàn)幅值頻率可調(diào)，還可以獨立調(diào)節(jié)支撐相與擺動相的相位關(guān)系，易于實現(xiàn)六足機器人腿部控制。其數(shù)學(xué)模型為

令x=rcosφ，y=rsinφ，γ=ωt，極坐標(biāo)形式為

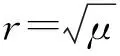
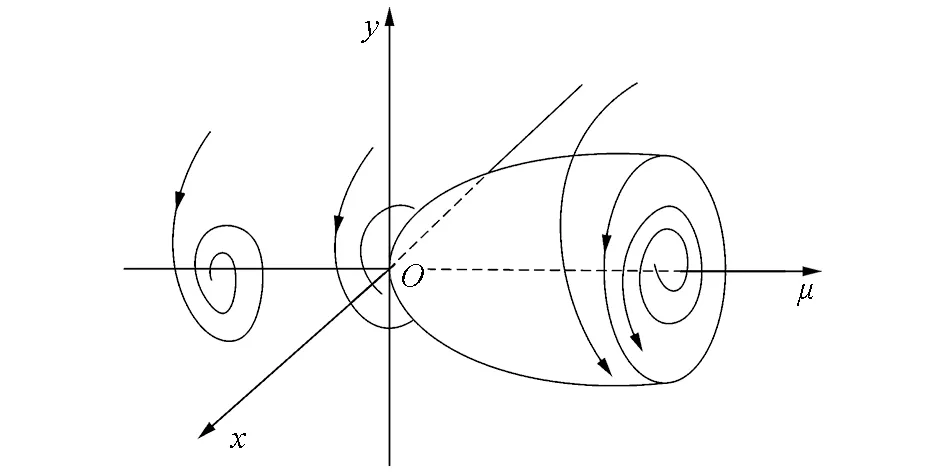
(a)μ變化的平衡點與極限環(huán)圖

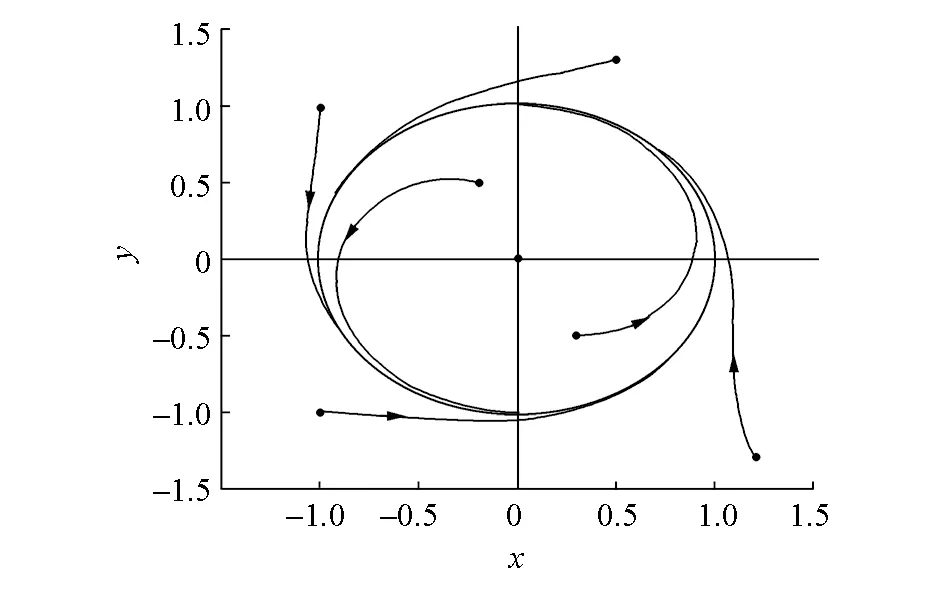
(b)x與y的相平面圖

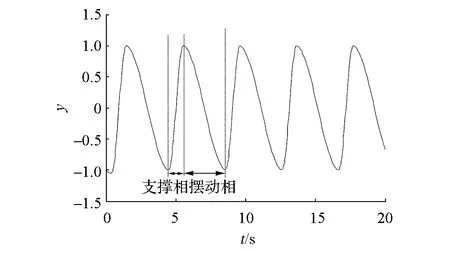
(c) 輸出y的振蕩曲線

由圖4(c)可見，該振蕩器能自發(fā)地產(chǎn)生穩(wěn)定的周期振蕩信號，方便調(diào)節(jié)上升和下降時間，從而很好地模擬了生物系統(tǒng)中的CPG神經(jīng)元。

要實現(xiàn)六足機器人腿部之間的協(xié)調(diào)運動，需要振蕩器的相互耦合，保證運動的同步性與協(xié)調(diào)性。耦合關(guān)系為

2.2 環(huán)形CPG網(wǎng)絡(luò)模型構(gòu)建

六足機器人的CPG網(wǎng)絡(luò)拓撲結(jié)構(gòu)由6個CPG單元構(gòu)成，每個CPG單元對應(yīng)六足機器人的一條腿，由Hopf振蕩器組成。采用加權(quán)有向圖構(gòu)成網(wǎng)狀結(jié)構(gòu)，6個CPG單元作為有向圖的6個頂點，相鄰頂點之間采用全對稱的雙向連接。CPG網(wǎng)絡(luò)拓撲結(jié)構(gòu)如圖6所示，在三角步態(tài)下，將腿分成{1，3，5}和{2，4，6}兩組。同組腿相位相同，異組腿相位相反。

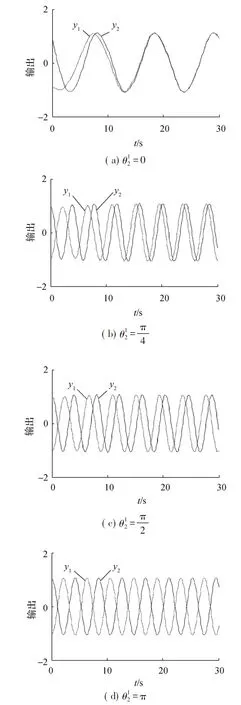
圖5 兩個耦合振蕩器不同相位差輸出波形圖

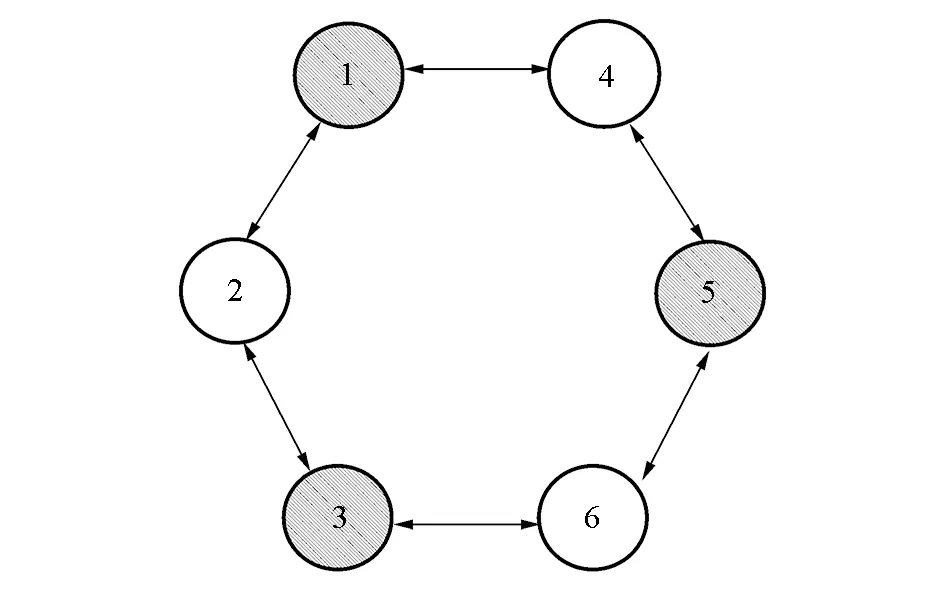
圖6 環(huán)形CPG網(wǎng)絡(luò)拓撲結(jié)構(gòu)圖

2.3 關(guān)節(jié)軌跡設(shè)計方案

六足機器人行走過程中，單腿關(guān)節(jié)角度具有如下規(guī)律：1)擺動相時，腿向前擺，髖關(guān)節(jié)角度增大，膝關(guān)節(jié)先正轉(zhuǎn)再反轉(zhuǎn)回到平衡位置，膝關(guān)節(jié)角度先增大后減小，踝關(guān)節(jié)轉(zhuǎn)角與膝關(guān)節(jié)變化規(guī)律相同；2)支撐相時，腿后擺，髖關(guān)節(jié)角度減小，膝關(guān)節(jié)與踝關(guān)節(jié)角度幾乎保持不變。

機器人有6條腿18個關(guān)節(jié)，如果每個關(guān)節(jié)都采用1個振蕩器，需要18個振蕩器，會使CPG網(wǎng)絡(luò)過于復(fù)雜，非線性微分方程階數(shù)過高，不利于CPG網(wǎng)絡(luò)的參數(shù)優(yōu)化和求解。

機器人在運動過程中，各關(guān)節(jié)之間相互配合，具有一定聯(lián)系。為了簡化模型結(jié)構(gòu)，采用膝踝映射函數(shù)，根據(jù)踝關(guān)節(jié)的轉(zhuǎn)角得到膝關(guān)節(jié)的轉(zhuǎn)角。單腿CPG控制規(guī)律如下：1個CPG單元對應(yīng)2個Hopf振蕩器，輸出信號相互耦合，分別控制髖關(guān)節(jié)、踝關(guān)節(jié)，膝關(guān)節(jié)信號通過膝踝映射函數(shù)得到。圖7為2個Hopf振蕩器生成的髖關(guān)節(jié)與踝關(guān)節(jié)的相位關(guān)系，其中y1為髖關(guān)節(jié)控制信號，y2為踝關(guān)節(jié)控制信號，調(diào)節(jié)兩者頻率值比為1:2，且兩者保持固定的相位差。

圖7 三角步態(tài)髖關(guān)節(jié)、踝關(guān)節(jié)相位關(guān)系曲線

選取CPG模型髖關(guān)節(jié)輸出曲線上升沿作為機器人擺動相，下降沿作為支撐相。根據(jù)機器人腿部擺動規(guī)律，對踝關(guān)節(jié)輸出進行調(diào)整，在支撐相時調(diào)節(jié)參數(shù)，使踝關(guān)節(jié)輸出趨向于零，符合實際規(guī)律。值得注意，兩個振蕩器耦合系數(shù)δ的取值會影響支撐相踝關(guān)節(jié)起始和末尾零值。當(dāng)δ>1時，踝關(guān)節(jié)輸出曲線振蕩不符合正弦函數(shù)；當(dāng)δ=0.35時，如圖8，踝關(guān)節(jié)輸出y21支撐相起始和結(jié)束位置數(shù)值有跳變；當(dāng)δ=0.01時，踝關(guān)節(jié)輸出y22支撐相基本趨于零值，關(guān)節(jié)輸出平滑且趨于零。

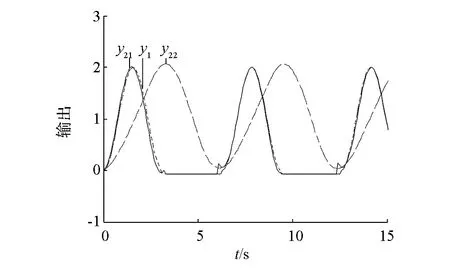
圖8 三角步態(tài)踝關(guān)節(jié)輸出優(yōu)化曲線

根據(jù)膝關(guān)節(jié)、踝關(guān)節(jié)的關(guān)節(jié)角度變化規(guī)律，將踝關(guān)節(jié)角度映射得到膝關(guān)節(jié)角度曲線，實現(xiàn)踝膝關(guān)節(jié)的耦合。單腿各個關(guān)節(jié)角度函數(shù)定義為

式中：k為比例系數(shù)，b為常數(shù)。調(diào)節(jié)k0、k1、k2、b1、b2使振蕩器輸出為髖關(guān)節(jié)、踝關(guān)節(jié)角度值。k3、k4、b3、b4為膝踝映射函數(shù)參數(shù)，參數(shù)b3、b4控制膝關(guān)節(jié)擺動幅度。

結(jié)合六足機器人機構(gòu)參數(shù)，取k0=0.8,k1=0.78,b1=1.01,k2=0,b2=0,k3=0.78,b3=π/2,k4=0,b4=π/2。為了區(qū)分不同腿的不同關(guān)節(jié)角度，對每條腿的每個關(guān)節(jié)角度進行定義：用θij表示，其中i表示腿的序號(i=1,2,3,4,5,6)，j=1表示髖關(guān)節(jié)，j=2表示踝關(guān)節(jié)，j=3表示膝關(guān)節(jié)。圖9為三角步態(tài)下兩條腿關(guān)節(jié)角度輸出曲線，其中組{1,3,5}擺動角度用實線表示，以腿1作為示例；組{2,4,6}擺動角度用虛線表示，以腿2作為示例。兩者相位相差為π。

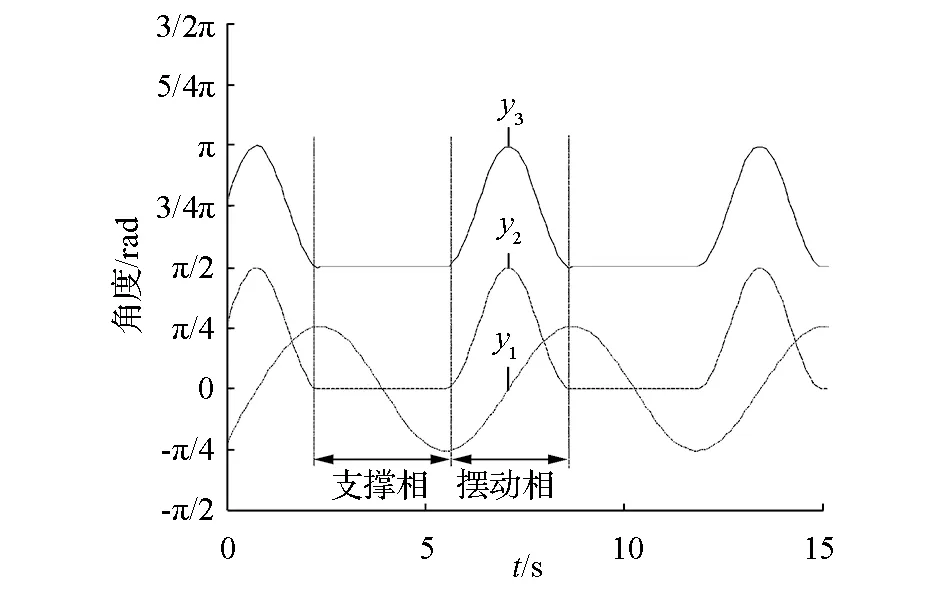
圖9 三角步態(tài)單腿三關(guān)節(jié)輸出曲線

根據(jù)前文正運動學(xué)分析，由機器人對應(yīng)時刻各關(guān)節(jié)角度，可求出六足機器人足端位置軌跡，從而推出六足機器人三角步態(tài)下的理論步長。圖10所示，點A1、A2、A3為機器人腿1在擺動相初始時刻髖關(guān)節(jié)、膝關(guān)節(jié)、踝關(guān)節(jié)角度，點B1、B2、B3為機器人腿1在擺動相結(jié)束時刻髖關(guān)節(jié)、膝關(guān)節(jié)、踝關(guān)節(jié)角度，A1=-0.796，A2=0.004，A3=1.58，B1=0.804，B2=0.008，B3=1.58，帶入(4)式，求得六足機器人理論步長為17.25 cm。

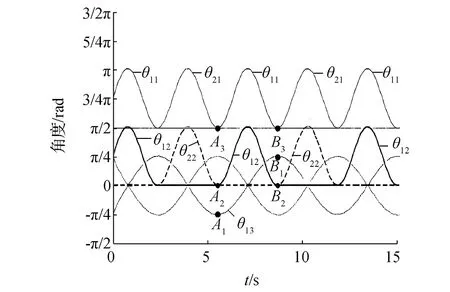
圖10 三角步態(tài)多足耦合三關(guān)節(jié)角度曲線

3 實物樣機驗證

為驗證基于Hopf振蕩器的六足機器人步態(tài)調(diào)節(jié)算法的有效性，本文搭建了六足機器人實驗平臺。六足機器人樣機采用KST X20-8.4-50伺服舵機驅(qū)動，控制器為Arduino USB 32路伺服舵機控制器。主要包括顯示模塊、無線通訊模塊、MPU6050模塊、舵機控制模塊。設(shè)計仿照六足螞蟻的腿部比例，表3為六足機器人主要參數(shù)。其中，基節(jié)L1長度為髖關(guān)節(jié)到膝關(guān)節(jié)軸線距離；股節(jié)L2為膝關(guān)節(jié)到踝關(guān)節(jié)軸線距離；脛節(jié)L3為踝關(guān)節(jié)到足端的軸線距離。

表3 六足機器人樣機主要參數(shù)

圖11為六足機器人三角步態(tài)行走實驗。實驗平臺上，每個短黑線間隔為20 m，樣機搭載液晶顯示，顯示當(dāng)前步態(tài)類型、振蕩器預(yù)設(shè)參數(shù)。實驗結(jié)果表明，機器人運動平穩(wěn)，步態(tài)協(xié)調(diào)。經(jīng)測量，六足機器人實際步長約為13.2 m,平均速度為6.45 m/s, 100 m內(nèi)直線運動略向左側(cè)平移4 m。機器人行走步長與理論步長有一定偏差，原因主要由于機構(gòu)設(shè)計髖關(guān)節(jié)預(yù)留空間不足，實際行走未達到理論角度，實驗中為避免關(guān)節(jié)發(fā)生碰撞，實際髖關(guān)節(jié)擺動范圍約為[-π/6, π/6]。

圖11 六足機器人三角步態(tài)行走實驗

4 結(jié)論

本文設(shè)計了一種六足機器人節(jié)律運動CPG模型，仿真和實驗表明：

1) 加入膝踝映射函數(shù)，可實現(xiàn)對六足機器人關(guān)節(jié)節(jié)律運動設(shè)計，簡化CPG耦合網(wǎng)絡(luò)模型；

2) 本文設(shè)計的關(guān)節(jié)映射函數(shù)參數(shù)合適，關(guān)節(jié)運動之間的相位關(guān)系合理；

3) 本文設(shè)計的CPG網(wǎng)絡(luò)能夠穩(wěn)定的生成機器人的運動關(guān)節(jié)角度，輸出結(jié)果較好的符合六足機器人三角步態(tài)的相位要求。

下一步將利用Hopf振蕩器相位可調(diào)優(yōu)點，進行六足機器人步態(tài)轉(zhuǎn)換研究，實現(xiàn)更復(fù)雜靈活的動作。

[1]JAN IJSPEERT A J. Central pattern generators for locomotion control in animals and robots: a review[J]. Neural networks, 2008, 21(4): 642-653.

[2]吳正興, 喻俊志, 譚民. 兩類仿鲹科機器魚倒游運動控制方法的對比研究[J]. 自動化學(xué)報, 2013, 39(12): 2232-2242. WU Zhengxing, YU Junzhi, TAN Min. Comparison of two methods to implement backward swimming for a carangiform robotic fish[J]. Acta automatica sinica, 2013, 39(12): 2232-2242.

[3]WU Xiaodong, MA Shugen. Adaptive creeping locomotion of a CPG-controlled snake-like robot to environment change[J]. Autonomous robots, 2010, 28(3): 283-294.

[4]高琴, 王哲龍, 趙紅宇. 基于Hopf振蕩器實現(xiàn)的蛇形機器人的步態(tài)控制[J]. 機器人, 2014, 36(6): 688-696. GAO Qin, WANG Zhelong, ZHAO Hongyu. Gait control for a snake robot based on Hopf oscillator model[J]. Robot, 2014, 36(6): 688-696.

[5]SEO K, CHUNG S J, SLOTINE J J E. CPG-based control of a turtle-like underwater vehicle[J]. Autonomous robots, 2010, 28(3): 247-269.

[6]LIU C J, FAN Z, SEO K, Fan Z, et al. Synthesis of matsuoka-based neuron oscillator models in locomotion control of robots[C]// IEEEProceedings of the Third Global Congress on Intelligent Systems (GCIS), 2012 Third Global Congress, Wuhan, China, 2012: 342-347.

[7]MATSUOKA K. Sustained oscillations generated by mutually inhibiting neurons with adaptation[J]. Biological cybernetics, 1985, 52(6): 367-376.

[8]FUKUOKA Y, KIMURA H, COHEN A H. Adaptive dynamic walking of a quadruped robot on irregular terrain based on biological concepts[J]. The international journal of robotics research, 2003, 22(3/4): 187-202.

[9]YU Junzhi, TAN Min, CHEN Jian, et al. A survey on CPG-inspired control models and system implementation[J]. IEEE transactions on neural networks and learning systems, 2014, 25(3): 441-456.

[10]BREAKSPEAR M, HEITMANN S, DAFFERTSHOFER A. Generative models of cortical oscillations: neurobiological implications of the Kuramoto model[J]. Frontiers in human neuroscience, 2010, (4): 190-14.

[11]JAN IJSPEERT A J, CRESPI A, RYCZKO D, et al. From swimming to walking with a salamander robot driven by a spinal cord model[J]. Science, 2007, 315(5817): 1416-1420.

[12]RIGHETTI L, JAN IJSPEERT A J. Pattern generators with sensory feedback for the control of quadruped locomotion[C]//Proceedings of IEEE International Conference on Robotics and& Automation. Pasadena, CA, USA, 2008: 819-824.

[13]MARK W. SPONG， S. HUTCHINSON, M. VIDYASAGAR. Robot modeling and con trol[M]. Hobokon, New Jekey, USA: John Wiley and Sons Inc., 2005: 65-74.

[14]于海濤. 基于非線性振子的 CPG 步態(tài)生成器及其運動控制方法研究[D]. 哈爾濱: 哈爾濱工業(yè)大學(xué), 2009: 10-11. YU Haitao. Research on CPG gait generator based on nonlinear oscillator and its locomotion control[D]. Harbin, China: Harbin Institute of Technology, 2009: 10-11.

[15]FRIGON A, ROSSIGNOL S. Experiments and models of sensorimotor interactions during locomotion[J]. Biological cybernetics, 2006, 95(6): 607-627.

任杰，女，1990年生，碩士研究生，主要研究方向為仿生機器人運動控制。

徐海東，男，1991年生，碩士研究生，主要研究方向為仿生機器人運動控制。

王斌銳，男，1978年生，博士，教授，主要研究方向為仿生機器人及其智能控制。

2017年IEEE先進智能機電一體化國際會議

The 2017 IEEE International Conference on Advanced Intelligent Mechatronics

July 3-7, 2017, Munich, Germany

The 2017 IEEE International Conference on Advanced Intelligent Mechatronics (AIM 2017) will be held on July 3-7 in Munich, Germany. The AIM 2017 conference brings together an international community of experts to discuss the state-of-the-art, new research results, perspectives of future developments, and innovative applications relevant to mechatronics, robotics, control, automation, and related areas.

The sponsors and organisers of AIM 2017 invite a submission of high quality mechatronics research papers describing original work, including the following topics: Actuators, Automotive Systems, Bioengineering, Data Storage Systems, Electronic Packaging, Fault Diagnosis, Human-Machine Interfaces, Industry Applications, Information Technology, Intelligent Systems, Machine Vision, Manufacturing, Micro-Electro-Mechanical Systems, Micro/Nano Technology, Modeling and Design, System Identification and Adaptive Control, Motion Control, Vibration and Noise Control, Neural and Fuzzy Control, Opto-Electronic Systems, Optomechatronics, Prototyping, Real-Time and Hardware-in-the-Loop Simulation, Robotics, Sensors, System Integration, Transportation Systems, Smart Materials and Structures, Energy Harvesting and other frontier fields.

Website: http://www.aim2017.org/

CPG model design based on hopf oscillator for hexapod robots gait

REN Jie, XU Haidong, GAN Su, WANG Binrui

(College of Mechanical and Electrical Engineering, China Jiliang University, Hangzhou 310018, China)

The key to bionic motion is a central pattern generator (CPG), which realizes the crawl gait of a hexapod. Firstly, the coordinate system of the robot was set up and the associated forward kinematics were solved based on D-H parameters. Hopf oscillators were then adopted into the design of coupling models involving multiple legs. A CPG ring topology structure was established using six CPG units, with each CPG unit consisting of two coupled Hopf oscillators, which output the hip and ankle joint signals, respectively. In order to control each joint (of a hexapod robot), a knee-ankle mapping function was used. The function mapped the output of the ankle to joint angles for both the knees and ankles. The number of oscillators in the CPG network was reduced using this method. Meanwhile, the coupling coefficient was changed to guarantee the phase interlock of adjacent oscillators and give a stable and smooth signal. Finally, a physical prototype was constructed for testing the robotic gait. The simulations and test results show that this CPG network has a stable phase difference, which ensures that hexapod robot can walk stably in a triangular gait and a crawling speed of approximately 6.45 cm/sec can be achieved.

central pattern generator; Hopf oscillator; hexapod robots; kinematic analysis

2016-01-28.

日期：2016-09-21.

國家自然科學(xué)基金項目(51575503);浙江省自然科學(xué)基金項目(LY14F030021).

王斌銳. E-mail：wangbinrui@163.com.

TP242

A

1673-4785(2016)05-0627-08

10.11992/tis.201601036

http://www.cnki.net/kcms/detail/23.1538.TP.20160921.1116.002.html

任杰，徐海東，干蘇，等.基于Hopf振蕩器的六足機器人步態(tài)CPG模型設(shè)計[J]. 智能系統(tǒng)學(xué)報， 2016, 11(5): 627-634.

英文引用格式：REN Jie, XU Haidong, GAN Su, et al. CPG model design based on hopf oscillator for hexapod robots gait[J]. CAAI transactions on intelligent systems, 2016,11(5): 627-634.