一個新分數階混沌系統的分析與同步
李 雪,薛 薇
(天津科技大學電子信息與自動化學院,天津 300222)
一個新分數階混沌系統的分析與同步
李 雪,薛 薇
(天津科技大學電子信息與自動化學院,天津 300222)
提出一個新的同量階2.7階分數階混沌系統,基于預估-校正時域法,采用Matlab繪制了該分數階混沌系統的相軌跡圖、Lyapunov指數圖和分岔圖,并用數值仿真驗證了該系統在一定參數變化范圍內存在混沌吸引子.研究該分數階混沌系統的同步問題,基于極點配置方法以及擴展的非線性狀態觀測器理論,設計了一種投影同步方案.數值仿真與理論分析的結果一致,充分驗證了該同步方案的可行性和有效性.
分數階;混沌系統;狀態觀測器;投影同步;數值仿真
近年來,對于混沌理論及其應用的研究已經成為了科學界的熱點問題.各種新的混沌系統[1-3]不斷被發現和提出,促進了學者們對混沌理論的認識,豐富和完善了混沌學的研究內容,并且提高了混沌學在圖像加密、視頻加密、保密通信、故障診斷等領域的實際應用能力.自1983年Mandelbort[4]提出分數維以來,分數階微積分理論已取得了極其重大的進步.不同于整數階微積分,分數階微積分更注重函數的整體信息,因此在將混沌系統應用到實際工程領域時,分數階模型比整數階模型的應用范圍更廣泛,效果更明顯.這一現象促使越來越多的學者開始投身于研究和認識分數階混沌系統,例如已發現的有分數階R?ssler系統[5]、分數階Chen系統[6]、分數階Liu系統[7]、分數階Lü系統[8]、分數階廣義增廣Lü系統[9]等.
混沌同步是實現保密通信等混沌應用的基礎.隨著人們對分數階混沌系統的認識不斷深入,分數階混沌系統的同步問題得到了越來越多的關注.目前,已提出了很多分數階混沌系統的同步方法,諸如:線性反饋同步[10]、滑膜控制[11]、投影同步[12]、自適應同步[13]、廣義同步[14]等各種同步控制方法,這些同步方法的提出對混沌在實際工程領域的應用具有重要的意義.
本文提出一個新的同量階分數階混沌系統,給出了該分數階混沌系統的相軌跡圖、Lyapunov指數圖和分岔圖等特性.在此基礎上,應用狀態觀測器的投影同步方法對所給的新分數階混沌系統進行了同步研究.
1 新分數階混沌系統分析
1.1 數學模型
系統含有3個非線性項,其數學模型為
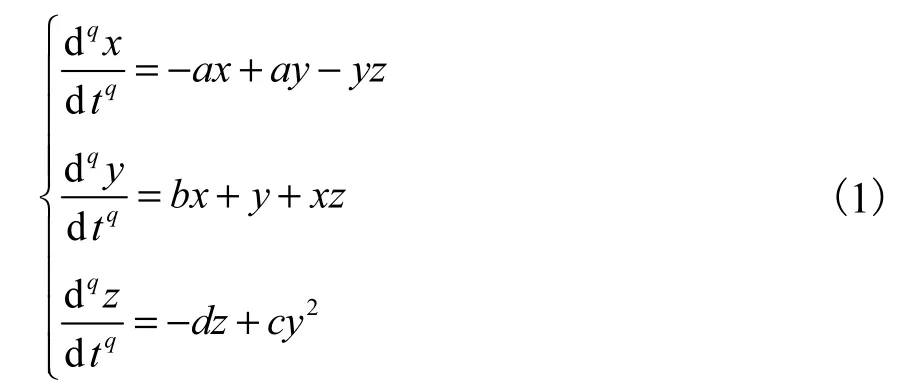
式(1)系統中各狀態變量的分數階微積分階次為q,且q∈(0,1),系統階次為3q,系統參數為a, b, c, d.
1.2 分數階次q對系統的影響
取a=34.4,b=50,c=3,d=15時,繪制式(1)系統隨階次q∈[0.7,1]變化的分岔圖,如圖1所示.由圖1可以看出:當q∈[0.7,0.874]時,系統處于周期或者穩定狀態;當q∈[0.874,1]時,系統狀態解開始出現混亂現象,說明系統處于混沌狀態.
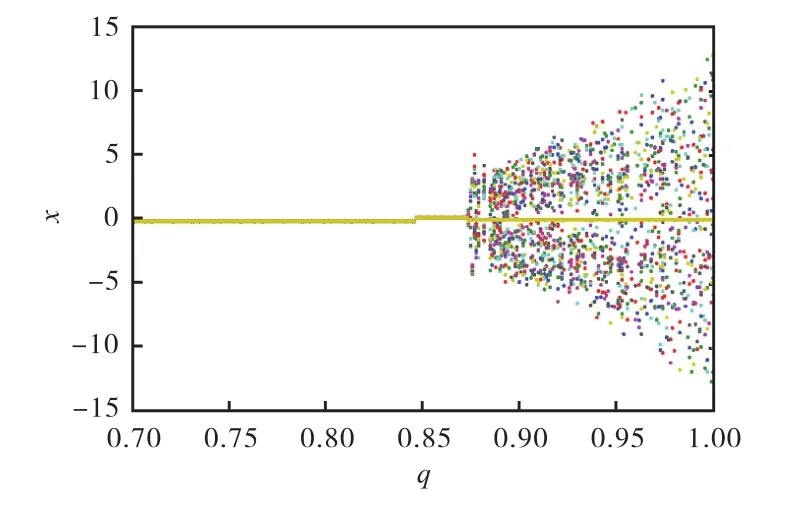
圖1 q∈[0.7,1]時式(1)系統在x軸上的分岔圖Fig. 1 Bifurcation diagram of system(1) on x axis when q∈[0.7,1]
1.3 相軌跡分析
為了方便觀察式(1)系統的混沌特性,本文選取分數階次q=0.9時的情況進行分析.當a=34.4,b=50,c=3,d=15,q=0.9時,繪制出2.7階系統的相軌跡圖如圖2所示.從圖2中可以觀察到式(1)系統的混沌吸引子具有豐富的幾何形狀和復雜的拉伸軌線.
1.4 Lyapunov指數及分岔圖
這里分析2.7階系統隨參數a變化時,系統的Lyapunov指數變化和分岔情況.固定參數b=50,c=3,d=15,當a∈[20,60]時,繪制式(1)系統的Lyapunov指數圖和分岔圖,分別見圖3和圖4.
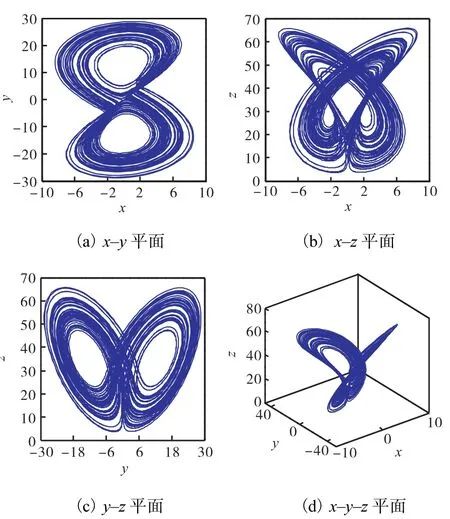
圖2 式(1)系統的相軌跡圖Fig. 2 Phase trajectory diagrams of system(1)
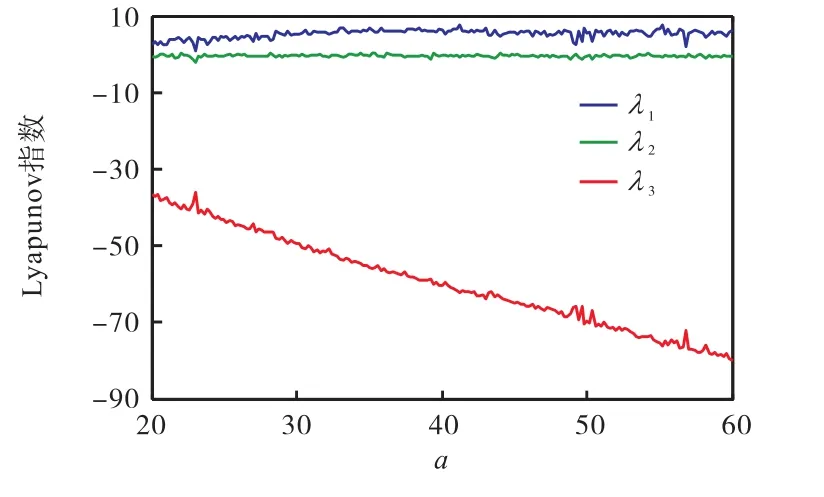
圖3 a∈[20,60]時式(1)系統的Lyapunov指數譜圖Fig. 3Lyapunov exponent diagram of system (1) when a∈[20,60]
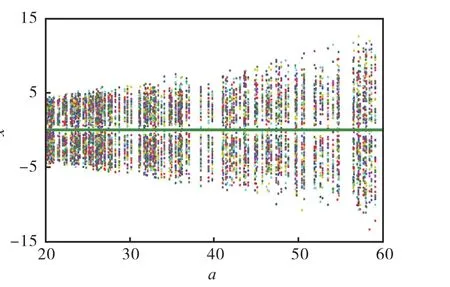
圖4 a∈[20,60]時式(1)系統在x方向上的分岔圖Fig. 4Bifurcation diagram of system(1)on x axis when a∈[20,60]
由圖3和圖4可以看出,系統隨參數a變化的分岔圖與其對應的Lyapunov指數譜圖保持一致.當參數a=34.4時,該系統的3個Lyapunov指數分別為λ1=6.4295,λ2=?0.215 2,λ3=?54.6645.其最大LE指數比目前很多分數階混沌系統的最大LE指數都大,如2.7階Chen系統[6](λ1=2.397 5)、2.7階Liu系統[7](λ1=0.0158)等.一般情況下,混沌系統的LE指數越大,其混沌特性越明顯,混沌程度越高.因此,本文提出的2.7階系統在圖像加密、保密通信等方面應該會有較好的應用前景.
2 同步控制器的設計
考慮如下兩個分數階混沌系統:
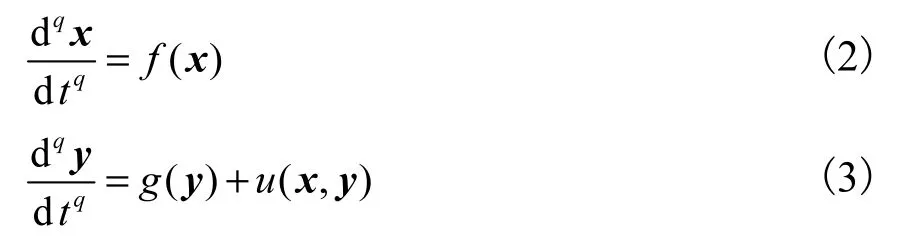
式中:狀態變量為x=(x12, x2,…,x)T∈Rn和y=(y1, y2,…,yn)T∈Rn;連續向量函數為f:Rn→Rn和g∶Rn→Rn;控制器為u( x, y).令式(2)和式(3)系統分別為驅動系統和響應系統.
定義1[15]假設?α,且α≠0,使得式(2)系統和式(3)系統滿足則稱以上兩個系統獲得了投影同步,其中α為狀態比例因子,為范數運算.
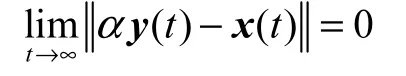
假設驅動系統為

式中:A∈Rn×n為Jacobian矩陣;B∈Rn×m為系數矩陣;F( x)為非線性項.響應系統(分數階狀態觀測器)滿足
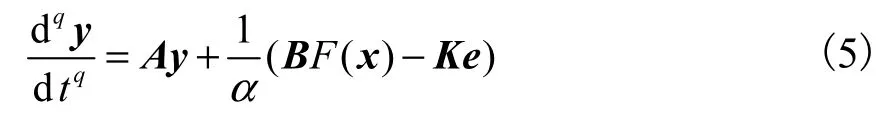
定義同步誤差為e=αy?x,則誤差系統為
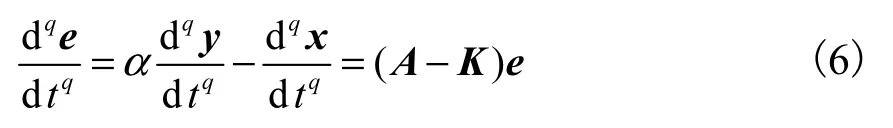
其中K∈Rn×n為誤差反饋增益矩陣.若矩陣(A?K)的特征值為負數,由分數階線性系統的穩定性理論可知,當時,有,則驅動系統和響應系統獲得了投影同步.
依據控制理論中的極點配置方法[16]適當地選取反饋增益矩陣K,使得矩陣(A?K)的特征值為負數,即可實現驅動系統和響應系統的投影同步.
以本文所提出的新分數階混沌系統為例,令驅動系統為
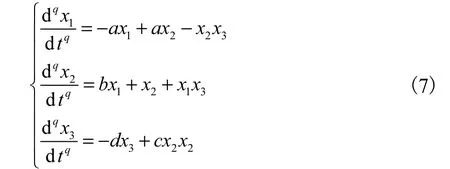
將驅動系統轉化為式(4)的形式,得到
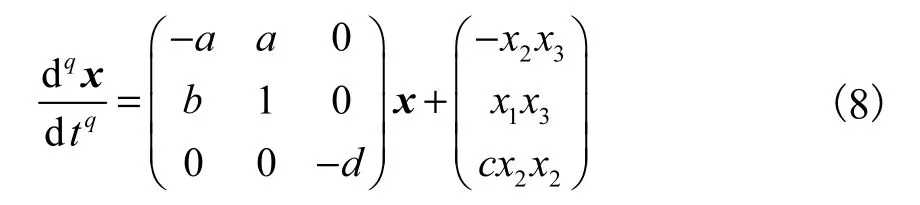
響應系統可以構造成
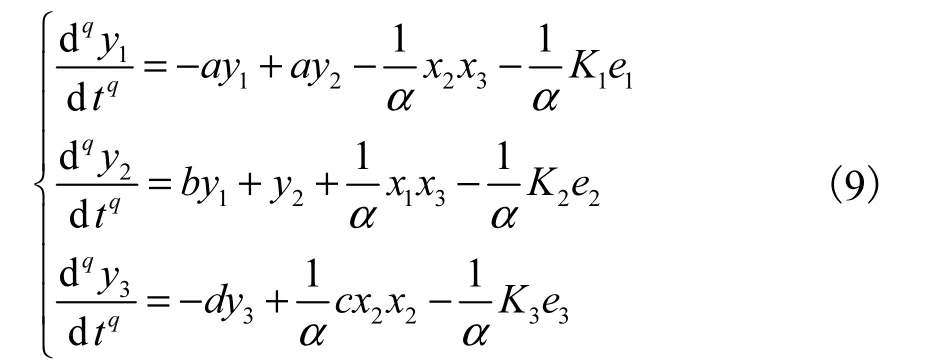
將響應系統轉化為式(5)的形式,得到
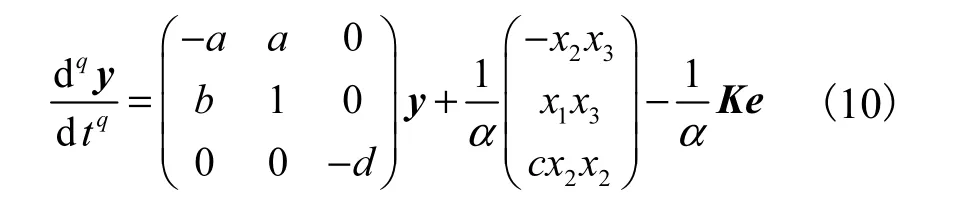
將式(8)和式(10)代入式(6),可得
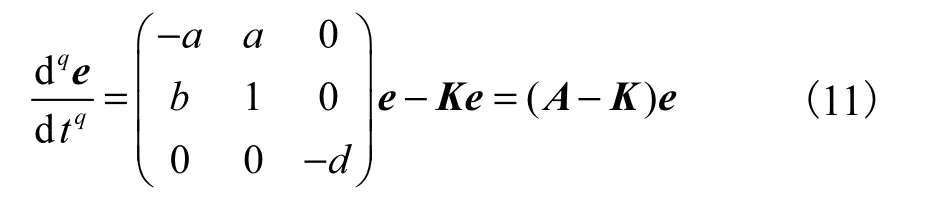
其中a=34.4,b=50,c=3,d=15,則系數矩陣A為
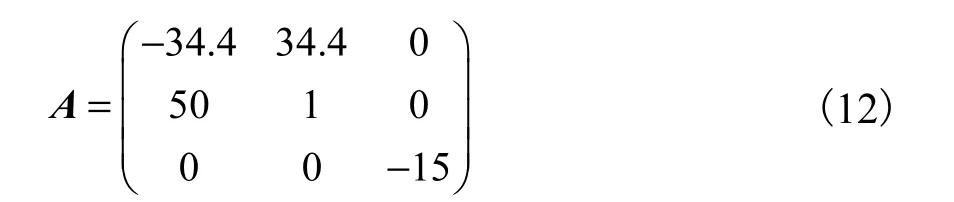
可見矩陣(A, I)可控,并且(I, AI,…,An?1I )是滿秩的.依據極點配置法選取反饋增益矩陣K為
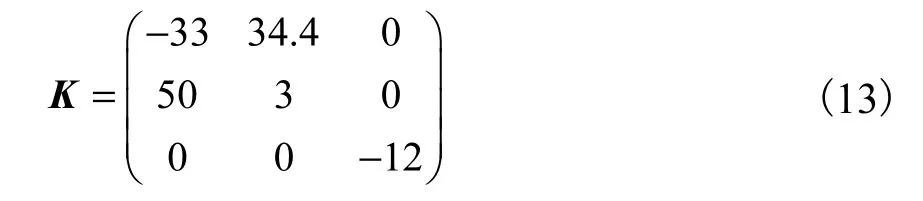
將式(12)和式(13)代入式(11),可得到誤差系統為

由于矩陣(A?K)的特征值為λ1=?1.5,λ2=?2,λ3=?3,也就是所有的特征值λi(i =1,2,3)全為負數.根據分數階線性系統的穩定性理論,可以得到即式(7)驅動系統和式(9)響應系統實現了投影同步.
3 同步仿真
運用預估-校正法進行數值仿真,選取的參數a=34.4,b=50,c=3,d=15,比例因子α=1,時間步長h=0.01,驅動系統和響應系統的初始值分別為x1(0)=?1,x2(0)=?2,x3(0)=?2,y1(0)=?1,y2(0)=?2,y3(0)=3,得到的數值仿真結果如圖5和圖6所示.由圖5可知,隨著時間的增加,驅動系統和響應系統狀態變量的運動軌跡完全一致.由圖6可以看出,誤差e1( t)、e2( t)、e3( t)可以在較短時間內漸近穩定于零,進一步說明該同步方法是可行的.
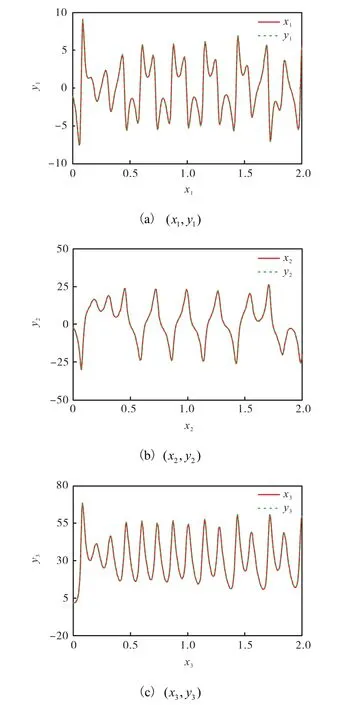
圖5 同步曲線圖Fig. 5 The synchronization curve
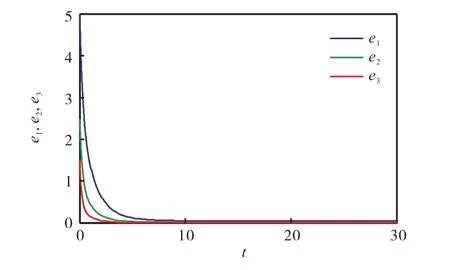
圖6 同步誤差隨時間的變化Fig. 6 Synchronization errors versus time
4 結 語
本文提出了一個新的分數階混沌系統,并對該系統的混沌特性進行了分析,運用Matlab軟件繪制了該2.7階新混沌系統的相軌跡圖、Lyapunov指數圖和分岔圖.數值仿真結果表明,該系統在較大參數變化范圍內存在混沌吸引子.在此基礎上,研究了該分數階混沌系統的同步問題,設計了一種投影同步方案,該同步方案依據極點配置法選取合適的反饋增益矩陣并對狀態比例因子進行簡單控制,所需的同步代價較小并且同步時間較短,具有一定的普遍性.通過理論分析和數值仿真充分驗證了該同步方法的可行性和有效性,為該分數階混沌系統在保密通信、圖像加密等實際工程中的進一步應用提供了技術支持.
[1] Liu C X,Liu T,Liu L,et al. A new chaotic attractor[J]. Chaos,Solitons and Fractals,2004,22(5):1031-1038.
[2] Qi G Y,Du S Z,Chen G R,et al. On a 4-dimensional chaotic system[J]. Chaos,Solitons and Fractals,2005,23(3):1671-82.
[3] 倉詩建,陳增強,袁著祉. 一個新四維非自治混沌系統的分析與電路實現[J]. 物理學報,2008,57(3):1493-1501.
[4] Mandelbrot B B. The Fractal Geometry of Nature[M]. New York:W H Freeman,1983.
[5] Li C G,Chen G R. Chaos and hyperchaos in the fractional order R?ssler equations[J]. Physica A,2004,341(2):55-61.
[6] 邵永暉,鐘啟龍,鄭永愛. 基于分數階Chen系統的圖像加密新算法[J]. 科學技術與工程,2014,14(2):159-164.
[7] 陳向榮,劉崇新,王發強,等. 分數階Liu混沌系統及其電路實驗的研究與控制[J]. 物理學報,2008,57(3):1416-1422.
[8] Lu J G. Chaotic dynamics of the fractional order Lü system and its synchronization[J]. Physics Letters A,2006,354(4):305-311.
[9] Xue W,Xu J K,Cang S J,et al. Synchronization of the fractional-order generalized augmented Lü system and its circuit implementation[J]. Chinese Physics B,2014,23(6):82-89.
[10] Yassen M T. Controlling chaos and synchronization for new chaotic system using linear feedback control[J]. Chaos,Solitons and Fractals,2005,26(3):913-920.
[11] Yau H T,Yan J J. Desgn of sliding mode controller for Lorenz chaotic system with nonlinear input[J]. Chaos,Solitons and Fractals,2004,19(4):891-898.
[12] Wang X Y,He Y J. Projective synchronization of fractional order chaotic system based on linear separation [J]. Physics Letters A,2008,372(4):435-441.
[13] Yassen M T. Adaptive chaos control and synchronization for uncertain new chaotic dynamical system[J]. Physics Letters A,2006,350(1/2):36-43.
[14] Wang T S,Wang X Y. Generalized synchronization of fractional order hyperchaotic lorenz system[J]. Modern Physics Letters B,2009,23(17):2167-2178.
[15] 王興元. 混沌系統的同步及在保密通信中的應用[M].北京:科學出版社,2012:320-330.
[16] Paraskevopoulos P N. Modern Control Engineering[M]. New York:Marcal Dekker,2002.
責任編輯:常濤
Analysis and Synchronization of a Novel Fractional-order Chaotic System
LI Xue,XUE Wei
(College of Electronic Information and Automation,Tianjin University of Science & Technology,Tianjin 300222,China)
In this research,a novel commensurate 2.7-order fractional-order chaotic system is proposed.The phase trajectory diagrams,the Lyapunov exponent spectra,and the bifurcation diagrams of the fractional-order chaotic system were establisher by using Matlab software and based on the predictor-corrector time domain method.The results imply there exists a chaotic attractor in the system with a certain range of change in system parameters.On this basis,the synchronization of the fractional-order chaotic system was investigated and a projection synchronization scheme based on the pole assignment method and the extended nonlinear state observer theory was designed.The simulation results are consistent with the theoretical analysis,which further demonstrates the feasibility and effectiveness of the proposed synchronization scheme.
fractional-order;chaotic system;state observer;projection synchronization;numerical simulation
TP391.9
A
1672-6510(2016)06-0069-05
10.13364/j.issn.1672-6510.20160004
2016-01-05;
2016-07-08
國家自然科學基金青年科學基金資助項目(11202148)
李 雪(1991—),女,河北人,碩士研究生;
薛 薇,教授,xuewei@tust.edu.cn.

