基于滑模觀測(cè)器的無(wú)速度傳感器異步電機(jī)模型預(yù)測(cè)控制

陳宇飛，王雨琦，陸 可，趙 洋，劉曉華

(1. 日立永濟(jì)電氣設(shè)備(西安)有限公司， 陜西 西安 710016；2. 西南交通大學(xué) 電氣工程學(xué)院， 四川 成都 610000)

?

基于滑模觀測(cè)器的無(wú)速度傳感器異步電機(jī)模型預(yù)測(cè)控制

陳宇飛1，王雨琦1，陸 可2，趙 洋2，劉曉華2

(1. 日立永濟(jì)電氣設(shè)備(西安)有限公司， 陜西 西安 710016；2. 西南交通大學(xué) 電氣工程學(xué)院， 四川 成都 610000)

模型預(yù)測(cè)控制是近年來(lái)在交流調(diào)速領(lǐng)域逐漸受到關(guān)注的一種優(yōu)化控制算法。針對(duì)預(yù)測(cè)控制所需的轉(zhuǎn)速和磁鏈信息，采用將電機(jī)本體輸出電流作為參考模型，自適應(yīng)磁鏈滑模觀測(cè)器的輸出電流作為可調(diào)模型，通過(guò)對(duì)電流誤差設(shè)置合適的自適應(yīng)率，最終辨識(shí)出轉(zhuǎn)速。該方案不僅提高了參考模型的精確性，同時(shí)將滑模理論應(yīng)用到磁鏈觀測(cè)模型，提高了系統(tǒng)的動(dòng)態(tài)響應(yīng)和對(duì)電機(jī)參數(shù)的魯棒性。最后在MATLAB/Simulink環(huán)境下搭建了聯(lián)合仿真模型，仿真結(jié)果驗(yàn)證了該方案的可行性。

模型預(yù)測(cè)控制； 滑模觀測(cè)器； 無(wú)速度傳感器； 異步電機(jī)

0 引 言

模型預(yù)測(cè)控制(Model Predictive Control, MPC)是一種經(jīng)典的最優(yōu)化控制方法，通過(guò)在采樣周期內(nèi)對(duì)所有電壓矢量的在線評(píng)估，選擇出滿足系統(tǒng)評(píng)價(jià)指標(biāo)的最優(yōu)電壓矢量，預(yù)測(cè)控制的優(yōu)點(diǎn)是在滿足非線性約束條件的同時(shí)，可保持較好的動(dòng)靜態(tài)性能。MPC本質(zhì)上是開(kāi)環(huán)最優(yōu)求解算法，其實(shí)時(shí)計(jì)算量較大，過(guò)去受限于微處理器的處理性能，因此在傳動(dòng)領(lǐng)域鮮有實(shí)際應(yīng)用，但隨著數(shù)字信號(hào)處理技術(shù)(Digital Signal Processor, DSP)的發(fā)展，使得在低成本處理器上實(shí)現(xiàn)復(fù)雜控制算法成為可能，也就促進(jìn)了MPC控制策略在電力傳動(dòng)領(lǐng)域的應(yīng)用研究。與矢量控制方案相比，MPC省去了電流內(nèi)環(huán)和參數(shù)整定，且無(wú)需脈沖調(diào)制。與直接轉(zhuǎn)矩控制方案相比，MPC通過(guò)對(duì)電機(jī)狀態(tài)的預(yù)測(cè)，選擇出最佳電壓矢量，使矢量選擇更加準(zhǔn)確有效，同時(shí)可考慮開(kāi)關(guān)頻率降低等非線性約束條件。

在高性能的交流傳動(dòng)系統(tǒng)中，準(zhǔn)確的速度反饋是獲得磁鏈信息的前提，而且在MPC系統(tǒng)中，轉(zhuǎn)矩給定值通常由給定轉(zhuǎn)速和實(shí)際轉(zhuǎn)速之差經(jīng)過(guò)速度PI得到，但速度傳感器的安裝降低了傳動(dòng)系統(tǒng)的可靠性，增加了維護(hù)成本。因此，無(wú)速度傳感器技術(shù)受到越來(lái)越多學(xué)者的關(guān)注與研究，其中基于滑模理論的速度辨識(shí)策略憑借動(dòng)態(tài)響應(yīng)快、魯棒性強(qiáng)、完全自適應(yīng)等優(yōu)點(diǎn)，一直是無(wú)速度傳感器技術(shù)的研究熱點(diǎn)[4-6]。S.Sanwonwanich提出了一種自適應(yīng)滑模觀測(cè)器的模型設(shè)計(jì)，在估算磁鏈的同時(shí)可辨識(shí)出轉(zhuǎn)速和定子電阻，與傳統(tǒng)觀測(cè)器相比具有全局穩(wěn)定的優(yōu)點(diǎn)；Marco Tursini提出了一種自適應(yīng)磁鏈滑模觀測(cè)器，并通過(guò)Liyapunov公式推導(dǎo)出轉(zhuǎn)速自適應(yīng)率。

本文采用基于轉(zhuǎn)子磁場(chǎng)定向思想的電流預(yù)測(cè)控制，在發(fā)揮模型預(yù)測(cè)多變量、多約束優(yōu)勢(shì)的同時(shí)，實(shí)現(xiàn)了轉(zhuǎn)矩、磁鏈和電流的分別控制。該方案省去空間矢量脈寬調(diào)制(Space Vector Pulse Width Modulation, SVPWM)，簡(jiǎn)化了系統(tǒng)結(jié)構(gòu)，加快了系統(tǒng)響應(yīng)速度。其次，在Marco Tursini的基礎(chǔ)上，通過(guò)仿真調(diào)試出最簡(jiǎn)增益矩陣，并把辨識(shí)轉(zhuǎn)速反饋給電流預(yù)測(cè)控制系統(tǒng)，仿真試驗(yàn)驗(yàn)證了該方案的可行性。

1 異步電機(jī)電流預(yù)測(cè)控制模型

1.1 異步電機(jī)離散數(shù)學(xué)模型

根據(jù)異步電機(jī)αβ坐標(biāo)系下的數(shù)學(xué)模型，可推導(dǎo)出以定子電流和磁鏈作為狀態(tài)變量的狀態(tài)方程：

(1)

其中：

A11=ωrJ-λ(RsLr+RrLs)I

A21=-RsI

A12=λRrI-λLrωrJ

A22=0

B1=λLrI

B2=I

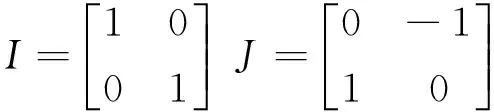
式中：ωr——電機(jī)轉(zhuǎn)子角速度； p——微分算子。

三相逆變器輸出電壓可表示為

(2)

式中：uan、ubn、ucn——逆變器三相輸出電壓；

Udc——直流母線電壓；

Sa、Sb、Sc——逆變器開(kāi)關(guān)狀態(tài)函數(shù)。

Sn=1表示上橋臂導(dǎo)通下橋臂關(guān)斷，Sn=0表示上橋臂關(guān)斷下橋臂導(dǎo)通(n=a、b、c)。

將式(2)經(jīng)過(guò)Clarke變換后代入式(1)得到基于開(kāi)關(guān)函數(shù)的電流狀態(tài)方程：

(3)

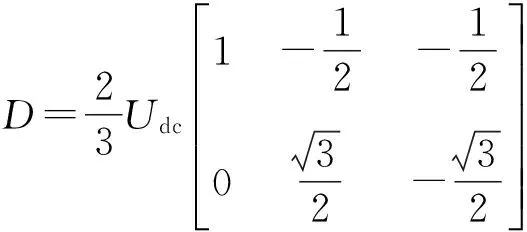
通常采樣時(shí)間Ts遠(yuǎn)小于電機(jī)電氣時(shí)間常數(shù)和機(jī)械時(shí)間常數(shù)，電機(jī)轉(zhuǎn)速在一個(gè)周期內(nèi)近似不變。用狀態(tài)變量is的差商代替微分，并采用前向歐拉法近似，得到異步電機(jī)離散狀態(tài)方程：

(4)

1.2 電流預(yù)測(cè)矢量控制

本文研究的電流預(yù)測(cè)控制基于異步電機(jī)轉(zhuǎn)子磁場(chǎng)定向，根據(jù)解耦思想可知，磁鏈調(diào)節(jié)器和轉(zhuǎn)矩調(diào)節(jié)器可獲得定子電流的勵(lì)磁分量ism和轉(zhuǎn)矩分量ist，通過(guò)Park變換得到兩相靜止坐標(biāo)系下的定子電流分量isα、isβ的指令值，最后通過(guò)設(shè)計(jì)的目標(biāo)函數(shù)來(lái)確定最優(yōu)開(kāi)關(guān)矢量。

為實(shí)現(xiàn)較低的電流脈動(dòng)和快速的跟蹤控制，本文采用k+1時(shí)刻預(yù)測(cè)值和指令值的α、β軸分量的誤差絕對(duì)值之和作為目標(biāo)函數(shù)：

(5)

當(dāng)采樣時(shí)間足夠短時(shí)，k+1時(shí)刻的指令值取當(dāng)前時(shí)刻的給定值：

(6)

2 定子磁鏈滑模觀測(cè)器

當(dāng)僅考慮轉(zhuǎn)子角速度誤差，不考慮其他參數(shù)產(chǎn)生的誤差時(shí)，根據(jù)式(1)可得到基于滑模理論的定子磁鏈觀測(cè)器模型，如式(7)和式(8)所示：

(7)

(8)

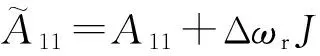
式中：上標(biāo)“～”——與轉(zhuǎn)速有關(guān)的的參數(shù)估計(jì)值；

上標(biāo)“ ^ ”——狀態(tài)變量觀測(cè)值；

sgn( )——符號(hào)函數(shù)；

K1——增量矩陣。

式(7)、式(8)分別減去式(1)可得到滑模觀測(cè)器的誤差函數(shù)：

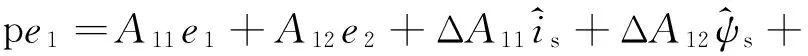
(9)

pe2=-LK1sgn(e1)

(10)

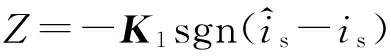
(11)

pe2=LZ

(12)

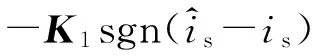
3 無(wú)速度傳感器方案

在電流傳感器采集準(zhǔn)確的前提下，本文以電機(jī)本體輸出電流作為標(biāo)準(zhǔn)模型，以自適應(yīng)滑模觀測(cè)器觀測(cè)出的電流作為可調(diào)模型，利用電流誤差構(gòu)成函數(shù)，通過(guò)合適的自適應(yīng)率實(shí)時(shí)調(diào)節(jié)可調(diào)模型中的待估參數(shù)(轉(zhuǎn)速)，以達(dá)到控制對(duì)象輸出跟蹤標(biāo)準(zhǔn)模型輸出的目的。基于滑模觀測(cè)器的無(wú)速度傳感器方案如圖1所示。

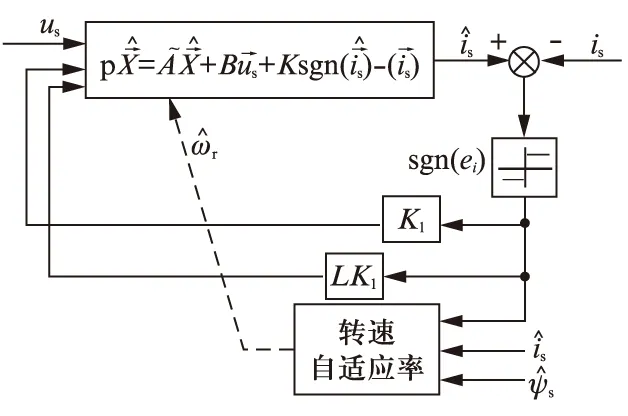
圖1 定子磁鏈滑模觀測(cè)器模型

根據(jù)Lyapunov第二穩(wěn)定性原理，定義如下函數(shù)：

(13)

令：

可得

pω=pω1+pω2

(14)

當(dāng)pω1<0且pω2=0時(shí)，有pω<0，滿足Lyapunov穩(wěn)定性條件。為滿足pω1<0，令

LT=-τA12,τ>0

(15)

當(dāng)pω2=0時(shí)，有

(16)

將式(15)代入式(16)，并整理得

(17)

式(17)為滿足Lyapunov穩(wěn)定性條件下的轉(zhuǎn)速自適應(yīng)收斂率。為提高動(dòng)態(tài)性能，采用式(18)所示PI轉(zhuǎn)速自適應(yīng)收斂率：

(18)

4 仿真試驗(yàn)

為驗(yàn)證基于滑模無(wú)速度傳感器技術(shù)的電流預(yù)測(cè)控制的正確性與可行性，搭建了基于MATLAB/Simulink的仿真模型，如圖2所示。仿真所用異步電機(jī)參數(shù)如下：PN=4kW，UN=380V，fN=50Hz，Rs=1.55Ω，Rr=1.25Ω，Lls=6mH，Llr=6mH，Lm=172mH，np=2，J=0.5kg·m2，電機(jī)空載起動(dòng)，0.65s時(shí)刻突加10N·m負(fù)載，起始給定轉(zhuǎn)速100rad/s，0.3s突變?yōu)?00rad/s，0.5s減小到150rad/s，采樣時(shí)間設(shè)置為1e-4s，仿真時(shí)間0.8s。

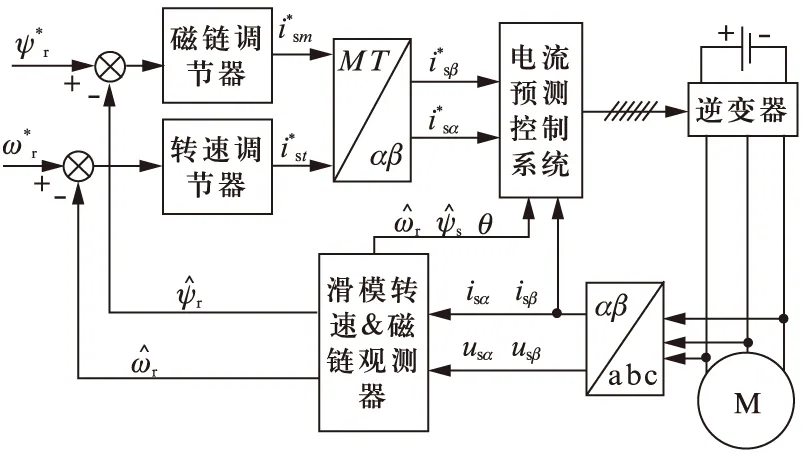
圖2 基于滑模無(wú)速度傳感器技術(shù)的電流預(yù)測(cè)控制模型

由圖3(a)可知，轉(zhuǎn)速辨識(shí)結(jié)果較準(zhǔn)確，但脈動(dòng)情況比較明顯，且誤差維持在±1.7rad/s內(nèi)，原因是滑模理論本質(zhì)上是一種非線性控制，通過(guò)在不同控制之間的切換，使系統(tǒng)達(dá)到預(yù)期值，故抖動(dòng)是不可避免的，因此在穩(wěn)定性方面稍有欠缺，但其動(dòng)態(tài)響應(yīng)快、魯棒性強(qiáng)、完全自適應(yīng)的優(yōu)點(diǎn)使其具有良好的應(yīng)用前景。由圖3(b)和圖3(c)可以看出，定子電流正弦性較好，與指令電流的誤差保持在±2A內(nèi)，通過(guò)對(duì)比不同采樣時(shí)間下的仿真結(jié)果發(fā)現(xiàn)，采樣時(shí)間越短，電流誤差越小。

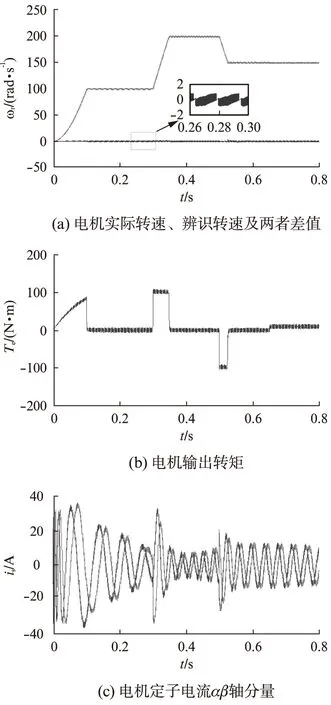
圖3 基于無(wú)速度傳感器技術(shù)的電流預(yù)測(cè)控制仿真結(jié)果

為驗(yàn)證電流預(yù)測(cè)控制在最佳矢量選擇方面優(yōu)于傳統(tǒng)的直接轉(zhuǎn)矩控制，基于MATLAB/Simulink仿真平臺(tái)，搭建了十八邊形磁鏈軌跡直接轉(zhuǎn)矩控制系統(tǒng)。圖4和圖5分別為兩種方案的仿真結(jié)果。

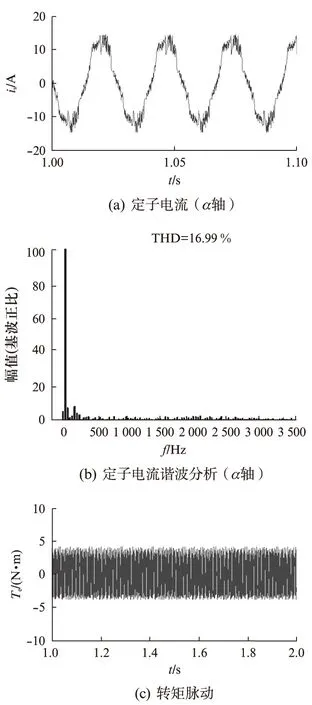
圖4 十八邊形磁鏈軌跡控制系統(tǒng)仿真結(jié)果

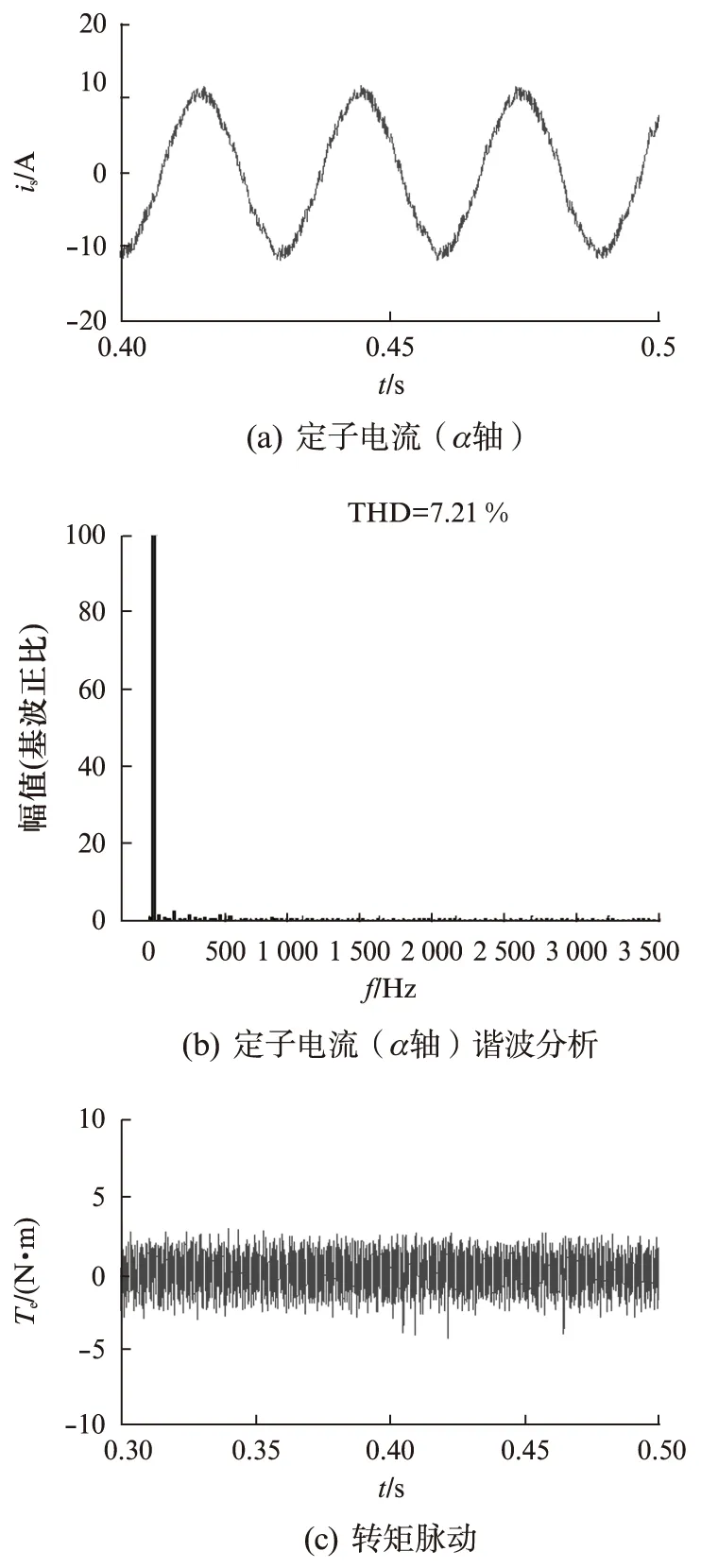
圖5 電流預(yù)測(cè)控制系統(tǒng)仿真結(jié)果

對(duì)比圖4和圖5所示仿真結(jié)果可知，在電流正弦性、諧波含量和轉(zhuǎn)矩脈動(dòng)方面，電流預(yù)測(cè)控制均優(yōu)于十八邊形磁鏈軌跡直接轉(zhuǎn)矩控制。究其原因，直接轉(zhuǎn)矩控制方案只考慮磁鏈和轉(zhuǎn)矩的動(dòng)態(tài)性能，僅通過(guò)磁鏈和轉(zhuǎn)矩的滯環(huán)選擇相應(yīng)的電壓矢量，而電流預(yù)測(cè)控制在考慮這兩個(gè)因素的同時(shí)，增加了電流正弦的約束條件，所選電壓矢量考慮的因素更加全面。但是，這是以降低轉(zhuǎn)矩動(dòng)態(tài)響應(yīng)為代價(jià)換來(lái)的，由圖5(c)可知，在電流預(yù)測(cè)控制方案中，轉(zhuǎn)矩的起始動(dòng)態(tài)響應(yīng)較慢。

5 結(jié) 語(yǔ)

本文基于定子磁鏈滑模觀測(cè)器推導(dǎo)出轉(zhuǎn)速自適應(yīng)率，并將該無(wú)速度傳感器方案應(yīng)用于電流預(yù)測(cè)控制系統(tǒng)，試驗(yàn)結(jié)果表明：(1) 基于滑模理論的無(wú)速度傳感器方案轉(zhuǎn)速辨識(shí)較為準(zhǔn)確，但不可避免的存在高頻抖振，對(duì)觀測(cè)器的消抖處理是下一步需要研究的方向；(2) 與傳統(tǒng)直接轉(zhuǎn)矩控制相比，電流預(yù)測(cè)控制在選擇最優(yōu)開(kāi)關(guān)矢量時(shí)，不僅滿足磁鏈和轉(zhuǎn)矩響應(yīng)，還可以滿足其他非線性約束條件。

[1]KENNELR,LINDERA.Predictivecontrolofinvertersuppliedelectricaldrives∥ProcofthePowerElectronicsSpecialistsConference, 2000：761-766.

[2] 張亞林.異步電機(jī)模型預(yù)測(cè)電流控制技術(shù)研究.武漢：華中科技大學(xué),2012.

[3] 楊耕,陳伯時(shí).交流感應(yīng)電動(dòng)機(jī)無(wú)速度傳感器的高動(dòng)態(tài)性能控制方法綜述.電氣傳動(dòng), 2001，31(3)：3- 8.

[4] SANGWONGWANICH S, DOKI S, YONEMOTO T, et al. Adaptive slidling observers for direct field-oriented control of induction ∥Conference of the IEEE Industrial Electronics Society,1990：915-920.

[5] 高仁璟，李希偉.PMSM無(wú)傳感器控制的新型滑模觀測(cè)器設(shè)計(jì).電機(jī)與控制應(yīng)用，2014，41(11)：7-13.

[6] 李明，程啟明，陳根，等.一種新型永磁同步電機(jī)滑模觀測(cè)器設(shè)計(jì)方法.電機(jī)與控制應(yīng)用，2015，42(6)：1-5.

[7] TURSINI M, PETRELLA R, PARASILITI F. Adaptive sliding-mode observer for speed-sensorless control of induction motors. IEEE Transactions on Industry Applications, 2000,36(5)：1380-1387.

[8] 馮曉云.電流牽引交流傳動(dòng)及其控制系統(tǒng).北京：高等教育出版社,2009.

[9] 廖永衡,馮曉云,王珍.基于定子磁鏈滑模觀測(cè)器的異步電機(jī)空間矢量調(diào)制直接轉(zhuǎn)矩控制.中國(guó)電機(jī)工程學(xué)報(bào),2012,32(18)：88-97.

Model Predictive Control Besed on Sliding-Mode Observer for Speed Sensorless Asynchronous Motor

CHENYufei1,WANGYuqi1,LUKe2,ZHAOYang2,LIUXiaohua2

(1. Hitachi Yonge Electric Equipment (Xi’an) Co., Ltd., Xi’an 710016, China;2. Electrical Engineering Institute Southwest Jiaotong University, Chengdu 610000, China)

Model predictive control (MPC) as an optimized control algorithm receiving attention gradually. Aiming at the desired parameters of speed and flux in MPC, proposed an adaptive observer which considering the motor current as reference model, and considering the Sliding Mode adaptive flux observer output current as adjustable model, then Lyapunov principle was applied to derive the speed adaptive algorithm. This method not only improved the precision of speed identification, but also ameliorate the dynamic response of system and parameters robustness. Finally, the speed sensor less MPC simulation model in MATLAB/Simulink environment was established, and the simulation results proved the effectiveness of this strategy.

model predictive control(MPC)； sliding-mode observer(SMO)； speed sersorless; asynchronous motor

陳宇飛(1990—)，男，碩士研究生，研究方向?yàn)殡娏﹄娮优c電力傳動(dòng)。 王雨琦(1991—)，男，碩士研究生，研究方向?yàn)殡娏﹄娮优c電力傳動(dòng)。 陸 可(1980—)，男，博士研究生，副教授，研究方向?yàn)殡娏﹄娮优c電力傳動(dòng)。

TM 301.2

A

1673-6540(2016)11- 0012- 05

2016-05-09